SOME PROPERTIES OF THE INTEGRATION OPERATORS ON THE SPACES F(p,q,s)*

(陈家乐)

School of Mathematics and Statistics, Shaanxi Normal University, Xi’an 710119, China E-mail: jialechen@snnu.edu.cn

Abstract We study the closed range property and the strict singularity of integration operators acting on the spaces F(p,pα-2,s).We completely characterize the closed range property of the Volterra companion operator Ig on F(p,pα - 2,s), which generalizes the existing results and answers a question raised in [A.Anderson, Integral Equations Operator Theory, 69 (2011), no.1, 87-99].For the Volterra operator Jg, we show that, for 0 ＜α ≤1,Jg never has a closed range on F(p,pα-2,s).We then prove that the notions of compactness,weak compactness and strict singularity coincide in the case of Jg acting on F(p,p-2,s).

Key words integration operator; closed range property; strict singularity

1 Introduction

LetH(D) denote the algebra of all analytic functions on the unit disk D={z:|z|＜1}of the complex plane C.Giveng ∈H(D), the Volterra type integration operatorJgis defined by

forf ∈H(D).The operatorJgwas introduced by Pommerenke[34]to give a novel proof of the analytic John-Nirenberg theorem.Since the pioneering works of Aleman, Cima and Siskakis[1-3], this operator has drawn much attention; see [5, 8, 11, 13-15, 20, 25, 30, 32, 35-39] and the references therein.The Volterra companion operatorIg, defined by

is closely related to the operatorJg; in fact, integration by parts gives that

whereMgis the multiplication operator defined byMgf=gf.

We next recall the function spaces on which we will work.For a pointa ∈D, letφadenote the M¨obius transformation of D that interchanges 0 anda, that is,

For 0＜p ＜∞,-2＜q ＜∞and 0≤s ＜∞, the spaceF(p,q,s) is defined as the space of allf ∈H(D) satisfying that

where dAis the normalized Lebesgue measure on D.It is known that, forp ≥1,F(p,q,s)/C is a Banach space with the norm‖·‖*,F(p,q,s).Subsequently, if we set

The class of spacesF(p,q,s)was introduced by Zhao[41],and contains a lot of classical function spaces as special cases, including weighted Bergman spaces, analytic Besov spaces, weighted Dirichlet spaces,α-weighted Bloch spaces, BMOA andQs-spaces; see [41, 43].

Our work also involves some other spaces of analytic functions;we review these now.Givenα ＞-1 and 0＜p ＜∞, the weighted Bergman spaceApαconsists of all functionsf ∈H(D)such that

It is clear thatFL(p,q,s)⊂F0(p,q,s).As usual, we useH∞to denote the space of bounded analytic functions on D equipped with the supremum norm.

It is easy to verify that ifq+s ≤-1, then the spaceF(p,q,s) contains only constant functions.Therefore, we always assume thatq+s ＞-1.For convenience, we will write thatq=pα-2,whereα ＞0.It is known that,for anyα ＞0,the spaceF(p,pα-2,s)is a subspace of theα-weighted Bloch spaceBα, and ifs ＞1, thenF(p,pα-2,s)=Bα.

Recently, Pau and Zhao [33] established the embedding theorems fromF(p,pα-2,s) into some tent spaces.As applications, they characterized the boundedness and compactness ofJgandIgacting onF(p,pα-2,s).Their results can be summarized as follows (see [33, Sections 5 and 6]):

Theorem 1.1Letα ＞0,s ＞0 andp ＞0 satisfy thats+pα ＞1, and letg ∈H(D).Then

(1) if 0＜α ＜1, the following conditions are equivalent:

(a)Jgis bounded onF(p,pα-2,s);

(b)Jgis compact onF(p,pα-2,s);

(c)g ∈F(p,pα-2,s);

(2)Jgis bounded (resp.compact) onF(p,p-2,s) if and only ifg ∈FL(p,p-2,s) (resp.g ∈FL,0(p,p-2,s));

(3)Igis bounded (resp.compact) onF(p,pα-2,s) if and only ifg ∈H∞(resp.g=0).

In this paper, we follow the line of research to investigate some other properties of integration operators on the spacesF(p,pα-2,s).

The first property we consider is the closed range property.Anderson[4]initiated the study of the closed range property of integration operatorsJgandIg, and characterized the closed range property of these operators on the Hardy space, weighted Bergman spaces and the Bloch space.We here consider the corresponding characterizations onF(p,pα-2,s).Noting thatIgmaps any constant function to the 0 function, we will consider the spacesF(p,pα-2,s)/C for the closed range property ofIg.To state our main result, recall that a Blaschke product is said to be interpolating if its zero sequence is an interpolating sequence forH∞.Our main result is the following:

Theorem 1.2Letα ＞0,s ＞0 andp ＞0 satisfy thats+pα ＞1, and letg ∈H∞.Then the following conditions are equivalent:

(a)Ighas closed range onF(p,pα-2,s)/C;

(b)g=BF, whereBis a finite product of interpolating Blaschke products andF ∈H(D)satisfiesF,1/F ∈H∞;

(c) There existr ∈(0,1) andη ＞0 such that, for allw ∈D,

Here, we useD(w,r) to denote the pseudohyperbolic disk with a centerw ∈D and a radiusr ∈(0,1); i.e.,D(w,r)={z ∈D:|φw(z)|＜r}.

We remark here that,sinceF(2,1,0)=H2,F(p,p+α,0)=Apαforα ＞-1,F(p,p-2,s)=Bfors ＞1,andF(2,0,s)=Qs(in particular,F(2,0,1)=BMOA),Theorem 1.2 is an essential generalization of [4, Theorem 3.9] and answers a question raised in [4, Concluding Remarks],where it was said that “we have partial results concerningSgbeing bounded below on BMOA,but have not completed proving a characterization like the one in Theorem 3.9”.

For the closed range property ofJg, we have the following result, which generalizes [4,Theorem 3.3]:

Theorem 1.3Let 0＜α ≤1,s ＞0 andp ＞0 satisfy thats+pα ＞1, and letg ∈H(D)such thatJgis bounded onF(p,pα-2,s).ThenJgdoes not have closed range.

Our second aim is to investigate the strict singularity ofJgandIgonF(p,pα- 2,s).Recall that a bounded linear operatorT:X →Ybetween Fr´echet spacesXandYis said to be strictly singular if its restriction to any infinite-dimensional subspaceM ⊂Xis not an isomorphism onto its range, i.e., the restriction is not bounded below onM.The notion of strict singularity was introduced by Kato [16].It is clear that any compact operator is strictly singular.Recently, there has appeared a variety of research concerning the strict singularity of some concrete operators on analytic function spaces; see [18, 19, 22, 23] for (weighted)composition operators and [9, 10, 17, 21, 28, 29, 31] for integration operators.Our main result on singularity, which indicates that the notions of compactness, weak compactness and strict singularity coincide in the case ofJgacting onF(p,p-2,s), is as follows:

Theorem 1.4Lets ＞0 andp ＞0 satisfy thats+p ＞1, and letg ∈H(D).Then the following conditions are equivalent:

(a)Jgis compact onF(p,p-2,s);

(b)Jgis weakly compact onF(p,p-2,s);

(c)Jgis strictly singular onF(p,p-2,s).

For the operatorIg, we also obtain that ifs+αmin{1,p} ＞1, then the compactness and strict singularity are equivalent forIgacting onF(p,pα-2,s) (see Theorem 3.9).

Throughout the paper, we writeA≾B(orB≿A)to denote that there is some inessential constantCsuch thatA ≤CB.IfA≾B≾A, then we write.

2 Closed Range Property

In this section, we study the closed range property of operatorsIgandJg.Before proceeding, we introduce some auxiliary results.

Recall that a linear operatorTon a quasi-Banach space(X,‖·‖)is said to be bounded below if there existsC ＞0 such that‖Tx‖ ≥C‖x‖for allx ∈X.Using the closed graph theorem,one can obtain the following characterization of closed range operators acting on quasi-Banach spaces (see [4, Theorem 3.2] for a proof):

Proposition 2.1LetXbe a quasi-Banach space and letTbe a one-to-one bounded linear operator onX.ThenThas closed range if and only if it is bounded below.

We remark here that,in the nontrivial cases,Jgis one-to-one onH(D),andIgis one-to-one onH(D)/C.Hence, to investigate the closed range property of these integration operators, we only need to consider the property of being bounded below.

We will need a characterization for reverse Carleson measures of Bergman spaces, which is essentially due to Luecking [26].The variant we use here can be found in [12, Corollary 3.34].Recall that, for an arcIon the unit circle T, the Carleson boxS(I) is defined by

where|I| is the normalized arc length ofIso that|T|=1.

Proposition 2.2Let 0＜p ＜∞,α ＞-1 and letτbe a bounded, nonnegative, measurable function on D.Forc ≥0, write thatGc={z ∈D :τ(z)＞c}.Then there existsC ＞0 such that the inequality

that is,Igis bounded below onF(p,pα-2,s)/C.Hence,in view of Proposition 2.1,(a)follows.

(a) =⇒(c): Assume that (c) fails.Fix∈＞0 and

Chooser ∈(0,1) such that (1-r2)θ ＜∈p.Since (c) fails, we can findw ∈D such that

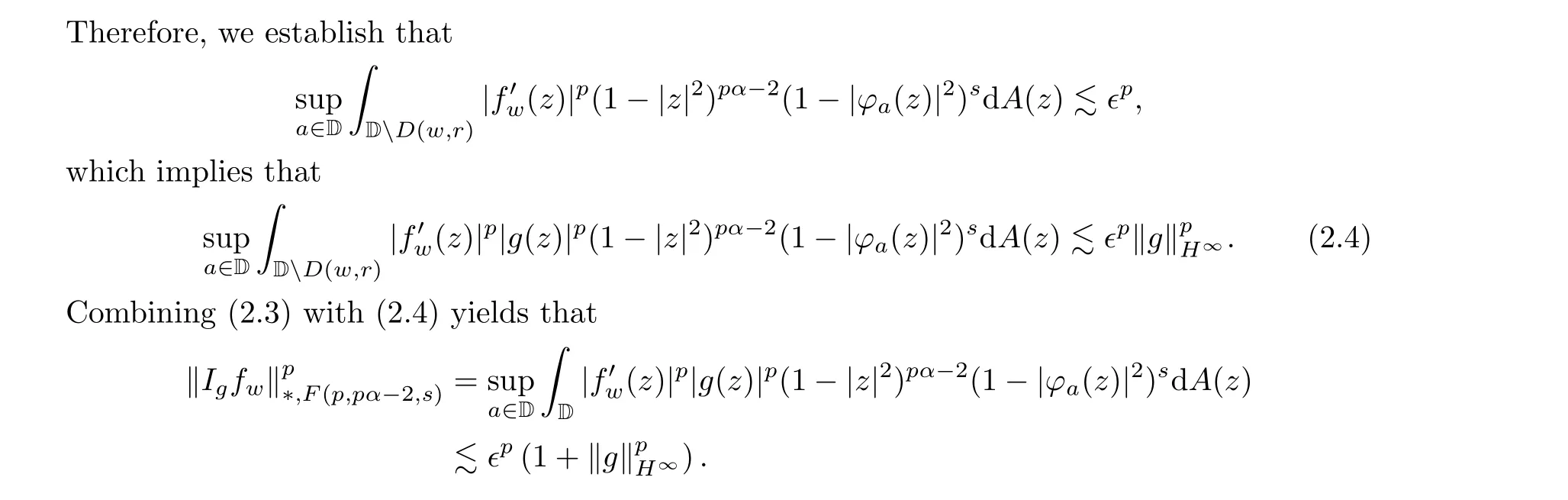
Since∈＞0 is arbitrary, we obtain thatIgis not bounded below onF(p,pα-2,s)/C, which finishes the proof for this case.

Therefore, in this case, we also have that‖Igf0‖*,F(p,pα-2,s)≾∈, which finishes the proof.□

Proof of Theorem 1.3In the case 0＜α ＜1, by Theorem 1.1,Jgis compact onF(p,pα-2,s), so it cannot be bounded below, and in view of Proposition 2.1, the desired result follows.

Suppose next thatα= 1.Then we have thatg ∈FL(p,p-2,s), due to Theorem 1.1.As before, we finish the proof by showing thatJgis not bounded below.This time we useen(z)=znas test functions.It is easy to see that, for anyn ≥1,en ∈F(p,p-2,s), and sinceF(p,p-2,s)⊂B,

Since∈＞0 is arbitrary, we conclude thatJgis not bounded below; this completes the proof.□

3 Weak Compactness and Strict Singularity

In this section, we investigate the weak compactness and strict singularity ofJbacting onF(p,p-2,s).Before proceeding, we give some preliminary results.

We first recall the concept of logarithmic Carleson measures.Givens ＞0 andp ≥0, a nonnegative Borel measureμon D is said to be a (p,s)-logarithmic Carleson measure if

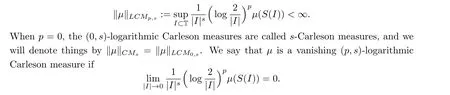
A vanishing (0,s)-logarithmic Carleson measure is also called a vanishings-Carleson measure.

The following equivalent description of(p,s)-logarithmic Carleson measures was established by Blasco [6] (see also [27, 42]):

Lemma 3.1Lets,t ＞0,p ≥0 and letμbe a nonnegative Borel measure on D.Then

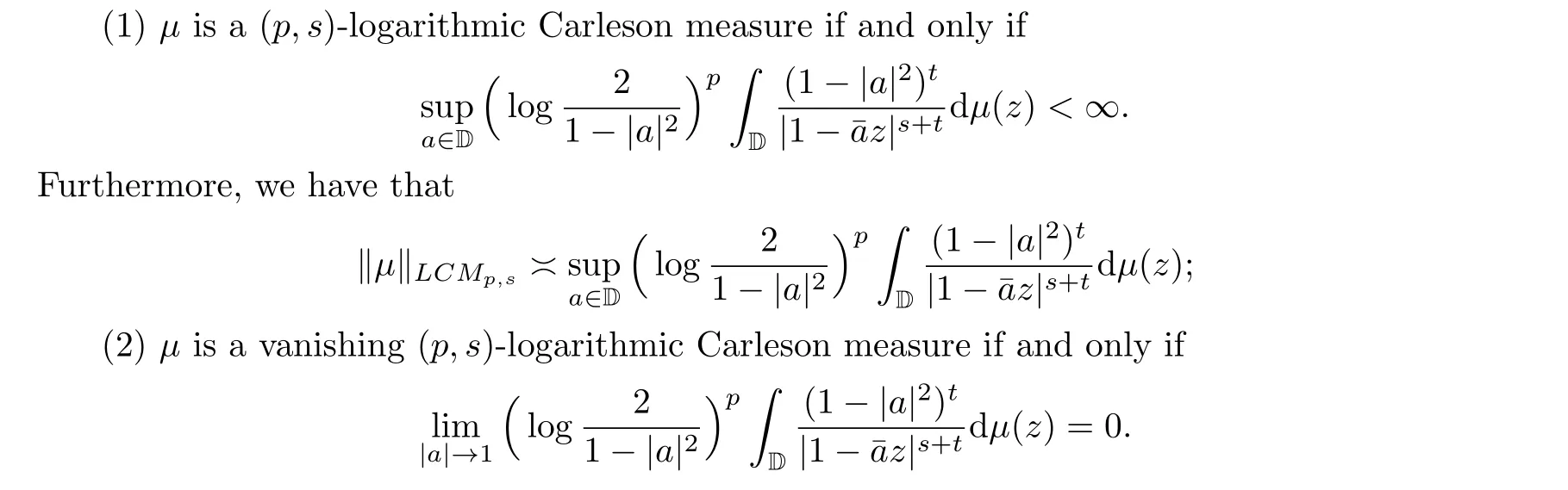
Based on the above lemma, we may give the Carleson measure characterizations for the spacesF(p,pα-2,s) andFL(p,pα-2,s).Fixα ＞0,s ＞0 andp ＞0 such thats+pα ＞1.For anyf ∈H(D), write that

belongs toF0(p,p-2,s).

ProofBy [33, Lemma 2.6], we know thatfb ∈F(p,p-2,s) and

that is,fb ∈F0(p,p-2,s).□

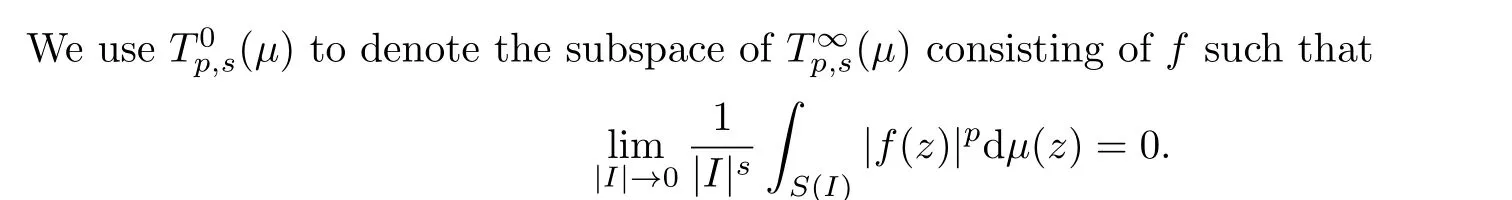
Proposition 3.3Lets ＞0 andp ＞0 satisfy thats+p ＞1, and letμbe a nonnegative Borel measure on D.Then the identity operatorI:F0(p,p-2,s)→T0p,s(μ) is bounded if and only ifμis a (p,s)-logarithmic Carleson measure.

ProofThe necessity follows from Lemma 3.2 and the proof of[33,Theorem 3.1].Suppose now thatμis a(p,s)-logarithmic Carleson measure.Then,by[33,Theorem 3.1],I:F(p,p-2,s)→T∞p,s(μ) is bounded.We only need to prove thatF0(p,p-2,s)⊂T0p,s(μ).Fix∈＞0.Since the polynomials are dense inF0(p,p-2,s)(see[24, Proposition 2.3]or[43, Theorem 3.10]), for anyf ∈F0(p,p-2,s), we may choose a polynomialhsuch that

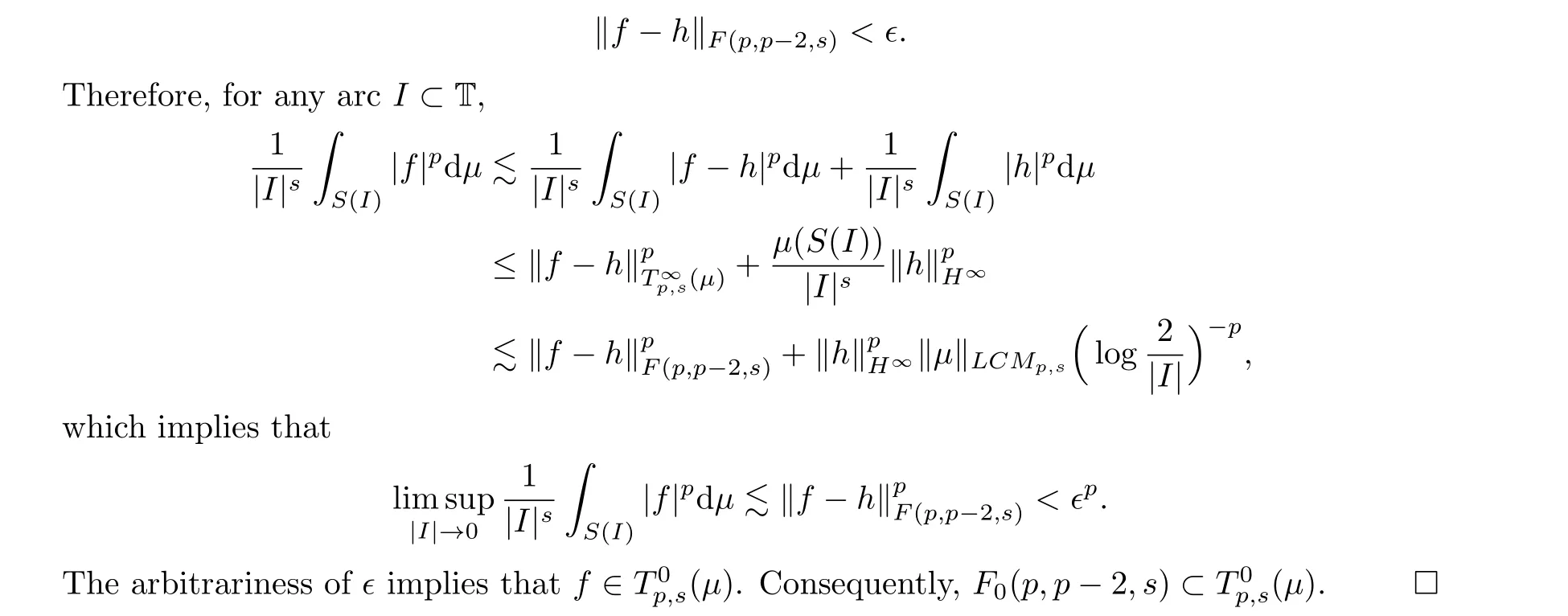
Using Proposition 3.3 and the same method as that used in the proof of [33, Theorem 5.1],we can obtain the following corollary immediately:

Corollary 3.4Lets ＞0 andp ＞0 satisfy thats+p ＞1, and letg ∈H(D).ThenJgis bounded onF0(p,p-s,s) if and only ifg ∈FL(p,p-2,s).

Our argument for Theorem 1.4 will depend on the following result,which is a generalization of [18, Proposition 6].As usual,c0denotes here the Banach space of complex sequences converging to zero endowed with the supremum norm‖·‖l∞.

Therefore,S(λ)∈F(p,pα-2,s).On the other hand, for anya ∈D andK ≥1,

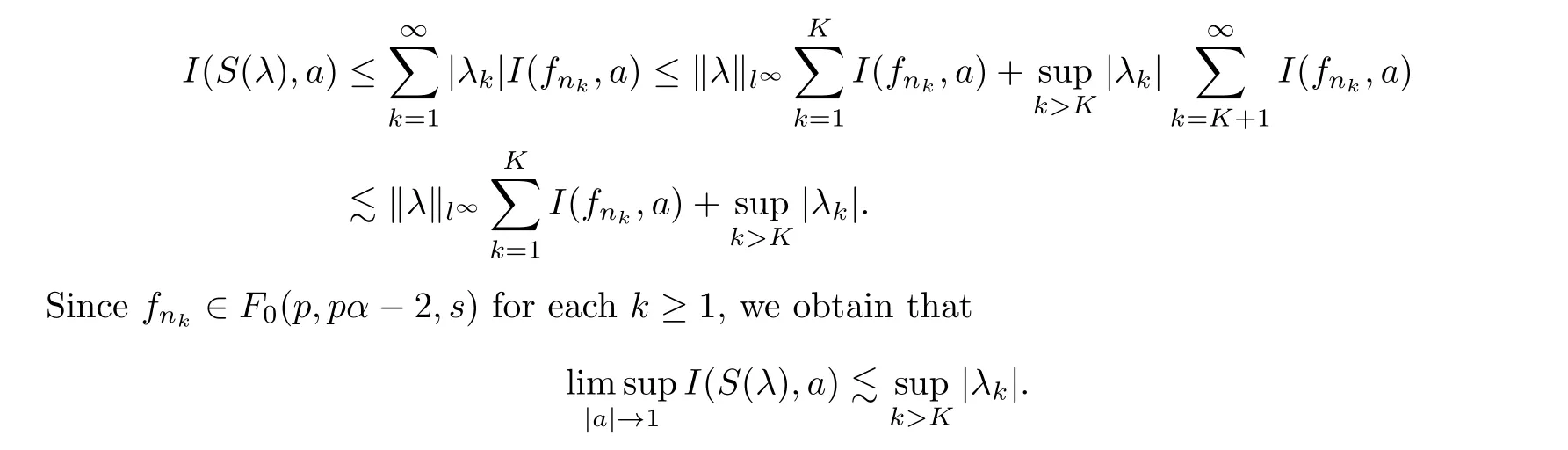
LettingK →∞then gives thatI(S(λ),a)→0 as|a|→1; that is,S(λ)∈F0(p,pα-2,s).Consequently,S:c0→F0(p,pα-2,s) is bounded.To show thatS:c0→F0(p,pα-2,s) is bounded below, note that, for anyλ={λk} ∈c0and anyl ≥1, the triangle inequality gives that

The following theorem is the last piece in the proof of Theorem 1.4:

Theorem 3.7Lets ＞0 andp ＞0 satisfy thats+p ＞1, and letg ∈FL(p,p-2,s)FL,0(p,p-2,s).Then there exists a subspaceM ⊂F(p,p-2,s) isomorphic toc0such thatJg|M:M →Jg(M) is an isomorphism.

ProofAs in Proposition 3.6, we only give the proof in the casep ≥1.The other case can be done similarly.

Sinceg ∈FL(p,p-2,s)FL,0(p,p-2,s), by (3.4)and(3.5), we can find a sequence of arcs{In}⊂T such that|In|→0 and

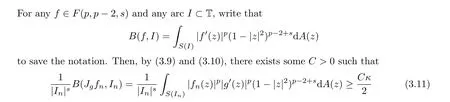
fornlarger than some (henceforth fixed)N ≥1.

Sinceg ∈FL(p,p-2,s),by Theorem 1.1,Jgis bounded onF(p,p-2,s),which implies that‖Jgfn‖F(p,p-2,s)≾1.Moreover,by Corollary 3.4,we know thatJgis bounded onF0(p,p-2,s),and consequently,Jgfn ∈F0(p,p-2,s)for eachn ≥1.Therefore,by the characterization(3.2),passing to a further subsequence if necessary, we may assume that, for anyn ≥N,

are both isomorphisms onto their respective ranges.Now letMbe the closure of span{hnk}inF0(p,p-2,s).ThenMis isomorphic toc0andJg|M:M →Jg(M) is an isomorphism.The proof is complete.□

We are now in a position to prove Theorem 1.4.

Proof of Theorem 1.4Since any compact operator is both weakly compact and strictly singular,we know that(a)implies both(b)and(c).Suppose now that(a)fails.We may assume thatJgis bounded onF(p,p-2,s); otherwise it cannot be weakly compact or strictly singular.Then, by Theorem 1.1 and Theorem 3.7, we know thatJgfixes an isomorphic copy ofc0inF(p,p-2,s).Sincec0is not reflexive, we conclude that neither (b) nor (c) holds.Therefore,the conditions (a), (b) and (c) are equivalent.□

Therefore, the series in the definition offconverges absolutely and uniformly on compact subsets of D.Consequently,f ∈H(D) and

Now, based on (3.1), (3.3) and Lemma 3.1, we can obtain thatf ∈F(p,pα- 2,s) with‖f‖F(p,pα-2,s)≾‖{λn}‖T∞p,s(Z).The details are similar as to the proof of [10, Theorem 3.4],and so are omitted.□

Based on Proposition 3.8, we can establish the following theorem, which asserts that ifα ＞0,s ＞0 andp ＞0 satisfy thats+αmin{1,p} ＞1, then the notions of compactness and strict singularity coincide in the case ofIgacting onF(p,pα-2,s).The proof is similar to[10,Theorem 5.3], and so is left to the interested reader.

Theorem 3.9Letg ∈H∞{0},α ＞0,s ＞0 andp ＞0 satisfy thats+αmin{1,p}＞1.Then there exists a separated sequenceZ ⊂D such that the operatorIg:F(p,pα-2,s)→F(p,pα-2,s) fixes an isomorphic copy ofT∞p,s(Z) insideF(p,pα-2,s); that is, there exists a subspaceM ⊂F(p,pα-2,s) which is isomorphic toT∞p,s(Z) and such that the restriction ofIgtoMis an isomorphism onto its range.In particular,Igis not strictly singular.

Conflict of InterestThe author declares no conflict of interest.