SOME NEW IDENTITIES OF ROGERS-RAMANUJAN TYPE*
(谷晶)
School of Mathematical Sciences, East China Normal University, Shanghai 200241, China 52215500005@stu.ecnu.edu.cn
Zhizheng ZHANG (张之正)
Department of Mathematics, Luoyang Normal University, Luoyang 471934, China;College of Mathematics and Information Science, Henan Normal University, Xinxiang 453001, China E-mail: zhzhzhang-yang@163.com
Abstract In this paper, we establish two transformation formulas for nonterminating basic hypergeometric series by using Carlitz’s inversions formulas and Jackson’s transformation formula.In terms of application, by specializing certain parameters in the two transformations,four Rogers-Ramanujan type identities associated with moduli 20 are obtained.
Key words Carlitz’s inversion; q-Series; Rogers-Ramanujan type identities
1 Introduction
We start with the standard notations and terminologies commonly used for basic (orq-)hypergeometric series (see, for example [1, 2]).We always assume that|q|<1.Theq-shifted factorial is defined for any real or complex parameteraby
and for the convenience of the reader, we also provide the following concise notation for the multipleq-shifted factorial:
Herenia an integer or∞.
It is known that combinatorial identities can be proven by applying reciprocal relations through the embedding method.In 1973, Gould and Hsu [3] discovered an extremely general pair of inverse series relations.Theq-analogue of this was established by Caritz [4] in the same year.Hsu communicated [3, Theorem 1] in a personal letter to Gould in 1965, but this has not been published.An essential transformation formula was established by Chu in [5,Theorem 3].Chu combined this formula with Jacobi triple identities to give a simple proof of Rogers-Ramanujan type identities.Chu and Di Claudio in [6] provided further details on Carlitz’s method of Rogers-Ramanujan identities.In [7], Liu found a transformation identity by employing the Carlitz inverse and Heine’s theorem.Many interesting theorems can also be found in[3].In[4],Carlitz proved aq-analogue of the reciprocal relation; here one can also find Carlitz’s inversions.
Theorem 1.1(Carlitz’s inversions formulas [4]) Letanandbnbe two sequences of complex numbers such that
for all nonnegative integersxandn, withφ(x;0) = 1.Then we have the following pair of reciprocal formulas:
For the polynomialsφ(x;n) = (λx;q)n, specified withak= 1 andbk=-qkλin Carlitz’s inversions,through the finite version of Kummer,and a rearrangement of the double sums,Chu[5], in 1990, established the following reciprocal series relations:
Theorem 1.2Letf(n) andg(n) be two sequences tied by one of the equations
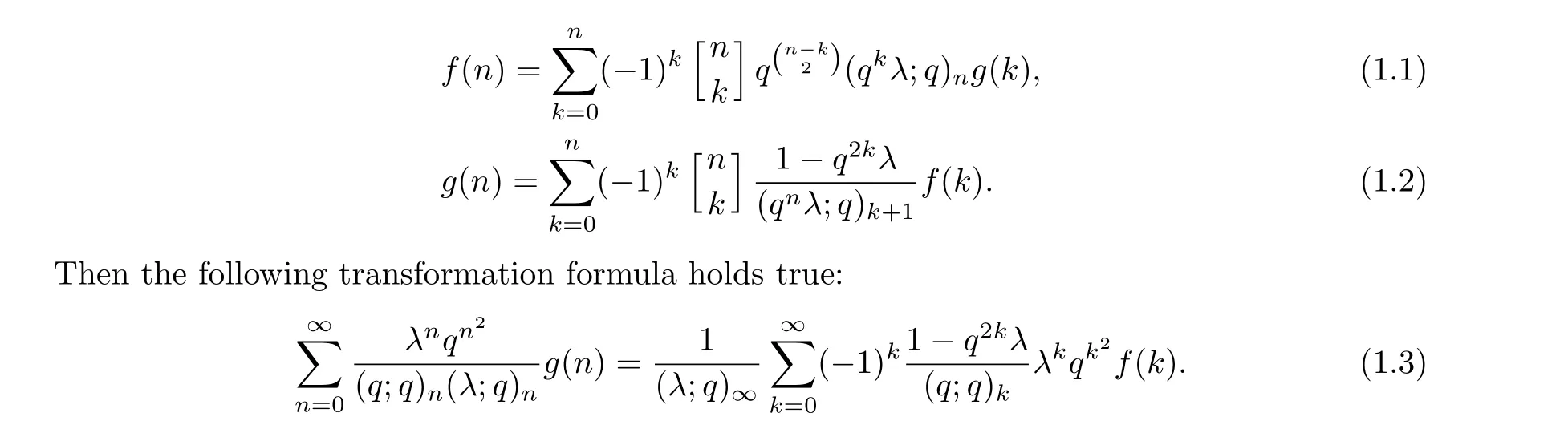
This theorem was utilized in the same paper to derive the celebrated Rogers-Ramanujan type identities.The Rogers-Ramanujan identities play a significant role in basic (orq-) hypergeometric series.The Rogers-Ramanujan identities [8] are given by the following: for|q|<1,
These identities, first proven by L.J.Rogers, were totally forgotten for over two decades.Ramanujan [9] rediscovered them in the 1910s, but without proof.The two sum-product identities have charming combinatorial interpretations, and have inspired many researchers in finding a wide range of identities.The first half of the identity is a proof from Rogers and the second half is a proof by Ramanujan,through the two proofs are essentially the same in[10].Schur [11] also published two different explanations.An underlying framework for the Rogers-Ramanujan identities was first discovering by Bailey [12, 13]; this eventually led to Slater’s list[14,15]of 130 identities of Rogers-Ramanujan type.Among the different approaches,the Bailey lemma has been shown to be a powerful method for discovering identities of Rogers-Ramanujan type [13-16].Chen and Chu [17] explored further applications regarding the reciprocal series relations and discovered numerous identities of Rogers-Ramanujan type for moduli 5, 7, 8, 10,14 and 27.For more work on the Rogers-Ramanujan identities we refer to [18-25].
The principal results of this paper are the following new Rogers-Ramanujan type identities:
Theorem 1.3For|q|<1, we obtain that
We will prove Theorem 1.3 in Section 3 by using the reciprocal series relations of Theorem 1.2.
Theorem 1.4For|q|<1, we get that
We will prove Theorem 1.4 in Section 4 by using the reciprocal series relations of Theorem 1.2.
Remark 1.5We note that Theorems 1.3 and 1.4 can be mutually deduced with the specification ofqby-q.
Combining Theorems 1.3 and 1.4, and by a direct computation, we can easily obtain the following corollaries:
Corollary 1.6([17, Corollary 5.4], [26], [27, eq.(2.3)]) For|q|<1, we have that

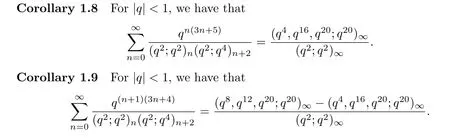
The purpose of this paper is to probe further into the possible applications of Carlitz’s inversion to Rogers-Ramanujan type identities.By Carlitz’s inversions formulas and Jackson’s transformation formula, two transformation formulas for nonterminating basic hypergeometric series will be established.As a result, by focusing on certain parameters in the two transformations, four Rogers-Ramanujan type identities associated with moduli 20 will be obtained.
2 Preliminaries
In this section, we collect some useful formulas and identities on the basic hypergeometric series.
We shall start from the basic (orq-) hypergeometric functionrΦs, withrnumerator andsdenominator parameters; that is defined by (see [1]; see also [2, p347, eq.(9.4)] and [31])
Theq-series in the above converges for all values ofzifr <1+s, and for|z|<1 ifr=1+s.
The basic hypergeometric series, which was a generalization of the hypergeometric series,was first considered by Heine [29, 30] and is given by defining, for|q|<1,|c|<1, that
Theq-binomial theorem plays an essential role in theq-series,which is defined in[1,(1.3.2)];see also [31, p92, eq.(3.2.2.11)]).For|z|<1 and|q|<1, and any complex numbera, we conclude that
The prominent Jacobi triple product identity is as follows (see, for example [20], [32]): for|q|<1 andx/=0, we find that
The equivalent form of Jackson’s transformation formula can be stated as follows[1,(1.5.4)]:for|q|<1 and|d/a|<1, and any complex numbera, we conclude that
The terminatingq-binomial theorem can be written in the following form [1, Ex.1.2 (ii)]:for|q|<1, we find that
whennandkare nonnegative integers.The following identity [1, (1.2.59)] is very helpful especially when dealing with some powers ofqthat appear in the derivations of theq-series formulas:
Bailey and Daum independently discovered theq-analogue of Kummer’s theorem (see, for example [12, p173], and also [20, p14, Entry 2], [33, p711]).In 1973, Andrews [34] gave theqanalogue of the celebratedq-Kummer’s theorem by taking advantage of a summation technique,which represented in the identity

Kim, Rathie and Lee [35, p154] derived the well-knownq-Kummer theorem using aq-integral representation.Furthermore, they adopted the same technique to deduce two results closely related to theq-Kummer theorem.
We also need the following essential identities closely related to theq-Kummer theorem from [35, eqs.(3.1), (3.2)]:
These identities were also obtained by Kim, Rathie and Choi[36, eqs.(3.4), (3.6)]in a different way.Harsh et al.[37,eqs.(6.125),(6.105)]gave a systematic study of theq-contiguous function relations and gave a new proof of the above two identities.
3 Proof of Theorem 1.3
In this section, we will give our proof of Theorem 1.3 by using Theorem 1.2 and a2φ1transformation formula (2.6).Before we start our proof, we first prove the following result:
Theorem 3.1We have that

where we used (2.4) and (2.5) in the second step and the Jackson transformation formula’s equivalence form (2.3).We can further reformulate the right hand side of the above formula as


Replacingλwithλq, lettingf(n),g(n) into (1.3) and then simplifying completes the proof of Theorem 3.1.□
We are now in the position to prove Theorem 1.3 by utilizing Theorem 3.1.
Proof of Theorem 1.3Settingλ=1 into Theorem 3.1, we deduce that

We then replaceqwithq2and simplify, and have the proof of the Rogers-Ramanujan identities stated in (1.4).
Settingλ=q2into Theorem 3.1, we obtain that
Here we replacekwith-k-1 in the second step, and can further reformulate the right hand side of the formula as

Substitutingq →q10,x →q10;q →q10,x →q8;q →q10,x →q8andq →q10,x →q6from the Jacobi triple product identity (2.2) into the third step, we obtain that
Replacingqwithq2and simplifying, we get the proof of the Rogers-Ramanujan type identities as stated in (1.5).□
4 Proof of Theorem 1.4
In this section, we will give our proof of Theorem 1.4 by using Theorem 1.2 and the2φ1transformation formula (2.7).Before we start our proof, we first prove the following result:
Theorem 4.1We have that
ProofWith the specification ofλwithλq, then substituting
into (1.1), we conclude that
Using(2.4)and(2.5)in the first step and the Jackson transformation formula’s equivalence form(2.3), we can further reformulate the right-hand side of the formula as

Ultimately, we find that
Replacingλwithλq, lettingf(n),g(n) into (1.3) and then simplifying completes the proof of Theorem 4.1.□
We are now in the position to prove Theorem 1.4 by utilizing Theorem 4.1.
Proof of Theorem 1.4 Settingλ=1 into Theorem 4.1, we deduce that
Usingk →-k-1 in the third and fourth terms of the fourth step, then substitutingq →q10,x →q6andq →q10,x →q8from the Jacobi triple product identity (2.2) into the first and second terms of the penultimate step, yields
Replacingqwithq2and simplifying, we get the proof of the Rogers-Ramanujan type identities stated in (1.6).
Settingλ=q2into Theorem 4.1, we obtain that
Replacingkwith-k-1 in the second step, we can further reformulate the right hand side of the formula as

Substitutingq →q10,x →q10;q →q10,x →q8;q →q10,x →q8andq →q10,x →q6from the Jacobi triple product identity (2.2) into the third step, we obtain that
Replacingqwithq2and simplifying, we get the proof of the Rogers-Ramanujan type identities stated in (1.7).□
Conflict of InterestThe authors declare no conflict of interest.
 Acta Mathematica Scientia(English Series)2024年1期
Acta Mathematica Scientia(English Series)2024年1期
- Acta Mathematica Scientia(English Series)的其它文章
- THE RIEMANN PROBLEM FOR ISENTROPIC COMPRESSIBLE EULER EQUATIONS WITH DISCONTINUOUS FLUX*
- THE BOUNDEDNESS OF OPERATORS ON WEIGHTED MULTI-PARAMETER LOCAL HARDY SPACES*
- AGGREGATE SPECIAL FUNCTIONS TO APPROXIMATE PERMUTING TRI-HOMOMORPHISMS AND PERMUTING TRI-DERIVATIONS ASSOCIATED WITH A TRI-ADDITIVE ψ-FUNCTIONAL INEQUALITY IN BANACH ALGEBRAS*
- INTERFACE BEHAVIOR AND DECAY RATES OF COMPRESSIBLE NAVIER-STOKES SYSTEM WITH DENSITY-DEPENDENT VISCOSITY AND A VACUUM*
- CONVEXITY OF THE FREE BOUNDARY FOR AN AXISYMMETRIC INCOMPRESSIBLE IMPINGING JET*
- SOME PROPERTIES OF THE INTEGRATION OPERATORS ON THE SPACES F(p,q,s)*
