基于最小二乘和自适应蛇优化算法的直驱风机LVRT 特性辨识

徐恒山，李文昊，赵铭洋，薛 飞，张旭军

（1.三峡大学电气与新能源学院，宜昌 443002；2.国网宁夏电力有限公司电力科学研究院，银川 750001；3.国网甘肃省电力公司电力科学研究院，兰州 730070）

近年来，风力发电占比的不断攀升给电力系统的安全稳定运行带来了巨大挑战[1]。直驱风机具有较强的非线性特性[2]，低电压穿越LVRT（low voltage ride through）控制参数作为并网逆变器控制参数的重要组成部分，是保证直驱风机连续运行的关键参数[3]，若偏差较大，逆变器将无法提供正确的功率，从而导致过电压、过电流甚至大规模脱网等一系列问题。为提高电力系统安全稳定运行能力，须对大电网进行快速、精确的仿真分析，因此机组的模型精度尤为关键。目前，机电暂态仿真模型应用最为广泛，风机的机电暂态模型一般忽略逆变器内环控制和锁相环动态过程[4]，但仍需考虑LVRT期间的电气特性，因此，获取准确的LVRT 控制参数至关重要。然而，我国风力发电设备厂商众多，不同厂商和型号的设备结构各异，且并网特性差异显著。若采用典型LVRT 控制参数，则难以准确模拟不同机型并网特性；若采用收资参数，往往又出于厂商保密原因，无法确保数据的完备性和准确性，影响单机和场站模型的精确性。

基于测试数据的参数辨识是获取新能源发电系统模型参数的有效途径，例如：文献[5]采用差分算法对内外环和LVRT 控制参数进行了解耦辨识，为LVRT 控制参数的独立辨识提供了思路，但未考虑LVRT 期间有功电流控制策略，因此LVRT 控制参数辨识的完备性不足。智能算法在新能源发电系统稳态下的内外环控制参数辨识中已得到广泛应用[6-7]，但在LVRT控制参数辨识的应用中，现有方法大多为粒子群优化PSO（particle swarm optimization）算法、最小二乘LS（least square）法等传统辨识方法，具有不可避免的缺陷，例如：文献[8-9]在考虑LVRT 有功电流控制策略的情况下，采用最小二乘法，结合实测数据实现了对风机LVRT 控制参数的快速辨识；文献[10]通过PSASP 和Matlab 平台联合仿真自动循环调用，采用PSO算法辨识了光伏逆变器LVRT 控制参数，但采用最小二乘法得到的辨识结果对极端工况适应性较差，需要对辨识结果进行人工调整，增加了辨识的复杂性，PSO 算法容易陷入局部最优，从而降低辨识精度；文献[11]通过自适应PSO 算法多次辨识提取最优值的方式，提高了辨识结果对工况的适应性，但存在多次辨识结果不一致的问题。为此，有必要提出一种辨识精度高、对极端工况适应性强且多次辨识结果具有一致性的辨识方法。

原始蛇优化SO（snake optimization）算法由Hashim 等[12]2022 年提出，通过模拟蛇在日常生活中觅食、战斗和交配的行为完成寻优。该算法比较新颖，具有双种群和多阶段寻优的特点，其后期寻优能力强、收敛速度快，但前期的种群多样性和收敛速度可能无法得到保证，因此算法精度有待提高。

本文将原始蛇优化算法与直驱风机LVRT控制产生辨识问题相结合，同时为解决原始SO 算法存在的缺点，提出了一种基于最小二乘和自适应蛇优化ASO（adaptive snake optimization）算法的直驱风机LVRT 控制参数辨识方法。利用LS 拟合参数不受初值影响的特点，完成对LVRT 控制参数的初步辨识，为ASO算法寻优提供有效的寻优范围。运用ASO 算法可准确、快速地完成6 个LVRT 控制参数的辨识。该算法在不同的寻优阶段采用了自适应学习因子，并在种群觅食阶段引入了Levy 飞行策略，大大减小了陷入局部最优的概率，有效提升了收敛速度和辨识精度。

1 典型LVRT 控制策略

1.1 LVRT 要求

为保证直驱风机在LVRT期间能够稳定运行，国家出台了标准GB/T 19963.1—2021《风电场接入电力系统技术规定第1部分：陆上风电》[13]，规定了LVRT期间并网曲线，如图1 所示。风机正常运行时，取逆变器侧到网侧的电流流向为正方向，此时流过并网逆变器的初始有功电流和初始无功电流分别为

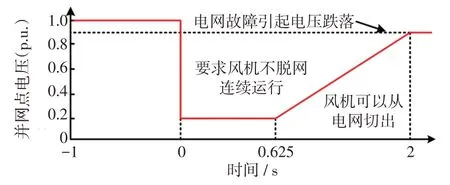
图1 风机LVRT 要求Fig.1 Requirement of LVRT for wind turbines

式中：Ip0和Iq0分别为初始有功电流和初始无功电流标幺值；P0和Q0分别为初始有功功率和无功功率标幺值；U0为并网点初始电压标幺值。

1.2 LVRT 控制策略

直驱风机进入LVRT 期间后，网侧逆变器内环的控制策略切换至LVRT控制策略。对于机电暂态模型，逆变器的LVRT 控制参数为关键参数，典型LVRT控制策略[14]如图2所示，各参数定义见表1。

表1 控制策略中的参数定义Tab.1 Definition of parameters in control strategy

图2 LVRT 控制策略Fig.2 Control strategy of LVRT

2 蛇优化算法

蛇的个体相当于在可行空间中的解，通过模拟蛇的生活习性完成寻优。种群受食物数量和当前温度两个因素的影响，在二者的共同作用下产生不同的行为。食物数量Q（t）和温度T（t）的计算公式为

式中：t和T分别为当前迭代次数和最大迭代次数；c1为学习因子。

当食物数量Q（t）低于阈值Q_th 时，种群进入勘探阶段进行全局搜索，通过生成随机个体决定种群位置的更新，公式为

式中：Xi,m和Xi,f分别为第i个雄性和雌性个体位置；Xmax和Xmin分别为种群位置的上、下边界；Xr,m和Xr,f分别为雄性和雌性种群中随机个体的位置；c2为学习因子；r为[0，1]之间的随机数；Am和Af分别为雄性和雌性个体寻找食物的能力，表示为

式中：fr,m和fr,f分别为雄性和雌性的随机个体适应度；fi,m和fi,f分别为第i个雄性和雌性的个体适应度。

当食物数量Q（t）高于食物数量阈值Q_th 时，从全局寻优转为局部寻优，若当前温度T（t）高于温度阈值T_th，种群位置更新公式为

式中：Xfood为食物位置；c3为学习因子。

若当前温度T（t）低于温度阈值T_th，则产生一个随机值model，当model 高于模式阈值model_th时，种群进入战斗模式，位置更新公式为

式中：Xbest,m和Xbest,f分别为雄性和雌性最佳适应度个体所在位置；Fm和Ff分别为雄性和雌性个体的战斗能力，公式为

式中，fbest,m和fbest,f分别为雄性和雌性种群的全局最佳适应度。

当model 低于模式阈值model_th 时，种群进入交配模式，位置更新公式为

式中，Mm和Mf分别为雄性和雌性个体的战斗能力，计算公式为

若交配后产生下一代个体，则用新一代个体替换种群中适应度最差的个体，重新初始化种群为

式中，Xworst,m和Xworst,f分别为雄性和雌性最差适应度个体的位置。文献[12]中的参数取值如表2所示。

表2 参数取值Tab.2 Values of parameters

3 自适应蛇优化算法

3.1 多阈值对种群行为的影响分析

SO 算法通过设定不同的阈值使得种群行为发生变化，并通过3 个固定的学习因子c1、c2和c3影响种群多样性和收敛速度。直驱风机LVRT控制参数辨识问题涉及多参数的同时辨识，由于寻优阶段众多，采用恒定的学习因子可能会导致种群多样性和收敛速度无法得到保证，进而影响到参数辨识结果的准确性，因此本文通过定量分析多个阈值对种群行为产生的影响，得到划分寻优阶段的边界条件。

由式（2）可知，食物数量和温度的初始值分别为Q（0）和T（0），终值分别为Q（T）和T（T），为完成勘探阶段寻优的全过程，食物数量阈值Q_th应满足Q（0）＜Q_th＜Q（T），此时Q_th与c1的关系为

式中，e ≈2.718

为完成开发阶段寻优全过程，温度阈值T_th应满足T（T）＜T_th＜T（0），则有

另外，将Q（t）=Q_th 时刻对应的迭代次数记为t1，将T（t）=T_th 时刻对应的迭代次数记为t2，若t1≥t2，种群完成勘探后将直接进入战斗或交配模式，因此，为完成开发阶段的全过程，还需满足t1＜t2。根据式（2）可知，t1和t2的计算公式为

根据温度阈值的第2 个约束条件t1＜t2，结合式（13），式（12）可以进一步写为

在式（11）和式（14）的约束下，种群行为发生变化的迭代区间为

从而得到Q（t）和T（t）变化曲线示意，如图3所示。

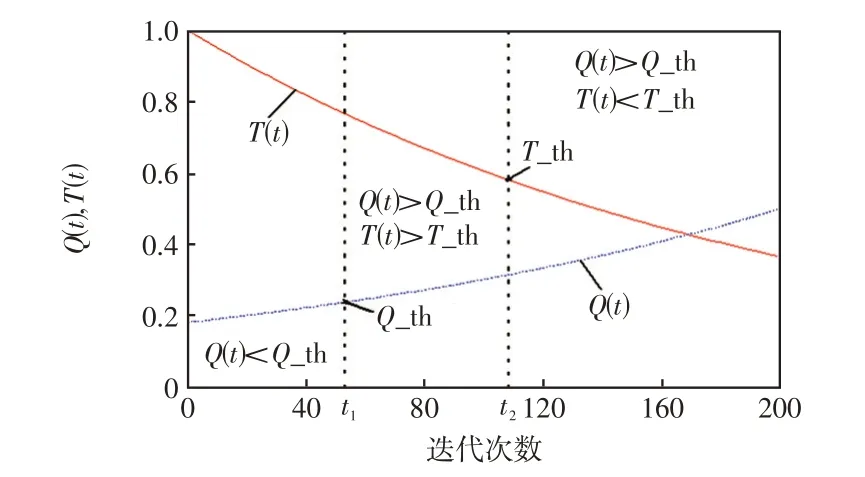
图3 Q(t)和T(t)变化曲线Fig.3 Variation curves of Q(t)and T(t)

3.2 分阶段自适应学习因子设计

SO 算法具有双种群和多阶段寻优的特点，且在不同寻优阶段更新种群位置时具有不同的比较机制，若采用单一的线性或非线性变化自适应学习因子，将难以满足上述需求，因此采用的自适应学习因子不应是单纯地随迭代次数变化的。为此，本文结合了不同的比较机制，对不同寻优阶段的种群行为进行动态调整，以全面改善种群的勘探和开发能力，使改进后的算法更适用于直驱风机LVRT 控制参数辨识。

1）阶段1(0～t1)：Q（t）＜Q_th。

在种群勘探阶段，根据式（13）可知，c1影响着种群勘探进程，取值较大时能够避免种群长期处于勘探阶段，从而有效提高参数辨识前期的收敛速度。在位置更新阶段，c2对偏差变量起放大作用，取值较大时能够保证种群多样性，取值较小时能够保证种群局部搜索能力，加快收敛速度。由于需要同时辨识出直驱风机的多个LVRT 控制参数，为实现种群多样性和收敛速度的动态调整，设计自适应学习因子c2m和c2f分别为

式中：c2max和c2min分别为c2的最大值和最小值；c2m和c2f分别为雄性和雌性个体的自适应学习因子。通过比较第i个个体和随机个体的适应度，自适应调整c2的大小。若fi,m(fi,f)≤fr,m(fr,f)，则通过增强种群多样性降低陷入局部最优的概率；否则，减小c2，提高局部寻优能力，加快收敛速度，从而在寻优过程中保持良好的种群多样性和局部开发能力，同时降低因局部搜索能力不足而导致辨识结果误差较大的问题。

2）阶段2(t1～t2)：Q（t）＞Q_th，T（t）＞T_th。

根据式（5）可知，c3控制着个体位置与当前食物位置间的距离。c3越小，个体下一次趋于向当前食物位置移动，若种群过早集中于单次迭代得到的全局适应度最佳个体所在位置，则容易出现早熟问题而陷入局部最优。种群全局最佳适应度是在多个比较机制共同作用下产生的，采用线性变化的自适应学习因子无法体现出与多个比较机制的内在联系，因此，设计非线性自适应学习因子为

式中：c3max和c3min分别为c3的最大值和最小值；c3m和c3f分别为雄性和雌性个体的自适应学习因子；fbest,p为种群全局最佳适应度；favg,m和favg,f分别为雄性和雌性所有个体适应度的平均值；favg为两个种群所有个体适应度平均值；Nm和Nf分别为雄性和雌性个体数；N为雄性和雌性个体总数。

相比传统的非线性自适应学习因子，本文考虑了不同阶段种群进化的差异性，结合了不同的比较机制，使自适应学习因子与种群觅食过程更加匹配，同时加强了动态调节能力。个体适应度越小，说明距离最优解越近，需要更强的局部开发能力，此时应缩小寻优范围；反之，距离最优解越远，需要增强种群的多样性以保证全局搜索能力，此时应扩大寻优范围。

3）阶段3(t2～T)：Q（t）＞Q_th，T（t）＜T_th。

阶段3 为种群在食物充足条件下发生战斗或交配行为的阶段，根据式（6）可知，c3控制着第i个个体与异性种群中最佳适应度个体位置之间的距离，取值较小时，个体下一次趋于保持当前位置不变，取值较大时则移向异性最佳适应度个体位置。在开发阶段前期，为保证种群的多样性，减小陷入局部最优的概率，c3可取较大的值，但较大的c3不利于后期的局部寻优，从而降低收敛速度，因此，当进入战斗或交配模式后，宜采用不同于开发前期的学习因子，结合不同的比较机制进行自适应调整，并重新规定其边界值，以满足双种群开发的需要，提高寻优过程与模式的匹配度。

为此，对于进入战斗模式的个体，设计自适应学习因子c4m和c4f分别为

式中：c4max和c4min分别为c4的最大值和最小值；c4m和c4f分别为雄性和雌性个体的自适应学习因子。

对于进入交配模式的个体，设计自适应学习因子c5m和c5f为

式中：c5max和c5min分别为c5的最大值和最小值；c5m和c5f分别为雄性和雌性个体的自适应学习因子。

改进后的学习因子更符合双种群的特性，不再由单一的学习因子对种群位置的更新进行控制，其灵活性大大提升，通过比较fi,m、fi,f、fbest,m和fbest,f，即可实现两种模式下个体位置的动态更新。

3.3 Levy 飞行策略

Levy 飞行[15]是一种非高斯随机步态，行走的步长服从重尾的稳定分布，其飞行特点为长时间进行小步长随机游走，使得个体不会在同一位置停滞过久。针对SO算法寻优前期可能陷入局部最优的问题，引入Levy 飞行能起到增强局部搜索能力的作用，通过短距离的局部搜索和长距离的全局搜索，可以有效降低陷入局部最优的概率。本文将Levy飞行策略引入式（5）中的种群最优位置，根据当前位置与种群最优位置的距离进行位置更新，结合式（18）和（19）的自适应学习因子，式（5）可重新写为

式中：D为空间维度；levy(D)的计算公式为

式中：μ和ν分别服从N（0，σ2）和N（0，1）分布；β为常数；Γ为伽马函数。

3.4 ASO 算法性能测试

为检验ASO 算法的先进性，采用文献[16]中的6 种基准测试函数对SO 算法和ASO 算法进行仿真对比。将两种算法独立运行50 次，取50 次适应度曲线的平均值，得到如图4 所示的6 种基准测试函数λ1～λ6的平均收敛曲线。可见，对于单峰函数λ1和λ2，ASO算法能够迅速跳出局部最优，且收敛速度优于SO 算法；对于多峰函数λ3和λ4，ASO 算法的平均最佳适应度与理论最优值的误差为0；对于固定维多峰函数λ5和λ6，SO和ASO算法的平均收敛曲线具有相同的变化趋势，但ASO算法的平均适应度要优于SO算法。

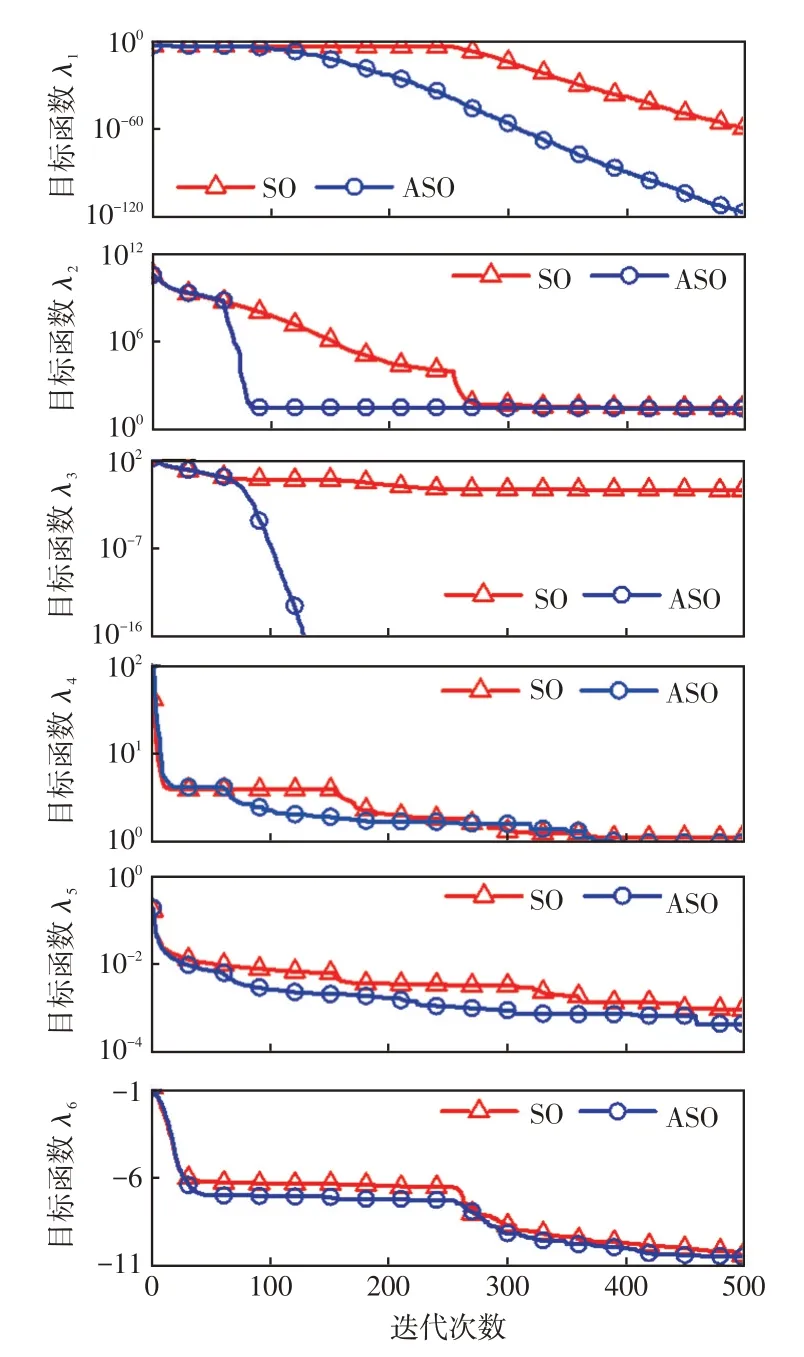
图4 函数优化收敛曲线Fig.4 Convergence curves of function optimization

将平均值和标准差作为算法性能的评价指标，其值越小则说明算法的性能越好。表3 为两种算法适应度的平均值和标准差，可见ASO算法的平均值和标准差值均小于SO 算法，由此表明ASO 算法比SO算法具有更好的寻优能力。

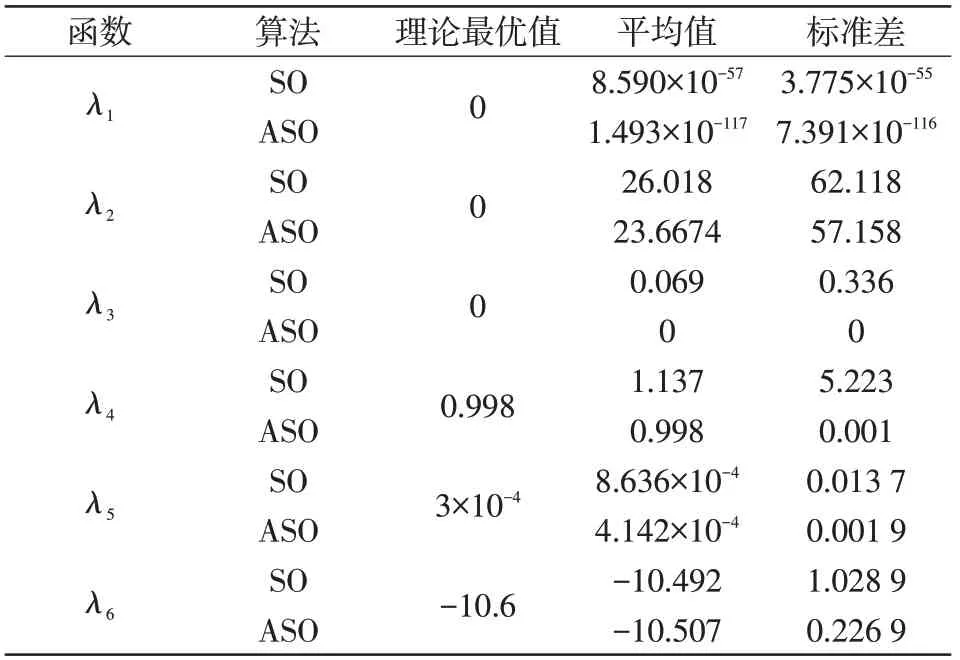
表3 测试结果对比Tab.3 Comparison of test results

4 LVRT 控制参数辨识

4.1 测试方案

如图5 所示为LVRT 测试示意，通过低电压发生装置模拟不同深度的电压跌落。本文在功率因数PF 分别为1.00 和0.95 下，设置初始有功功率P0从0.2 p.u.至1.0 p.u.，步长为0.2 p.u.，并在各P0下设置不同的电压跌落深度Ut分别为0.20 p.u.、0.35 p.u.、0.40 p.u.、0.50 p.u.、0.60 p.u.、0.75 p.u.、0.80 p.u.[17]，获取测量点1处的电压U、无功电流Iq、有功功率P和无功功率Q。

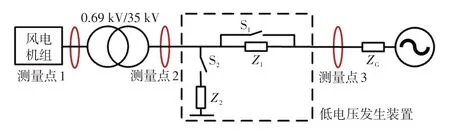
图5 低电压穿越测试示意Fig.5 Schematic of LVRT test

4.2 数据预处理

本文采用图2 中的无功电流控制策略和有功电流控制策略1 进行分析，将LVRT 期间未达到电流限制值的工况分布区域划分为线性工作区，其余工况分布区域为非线性工作区。如图6 所示为电流随初始有功功率分布的示意，以Imax=1.2 p.u.、KIq=1、Iqset=0，不同KUq下的电流响应为例，对工作区的划分进行分析。

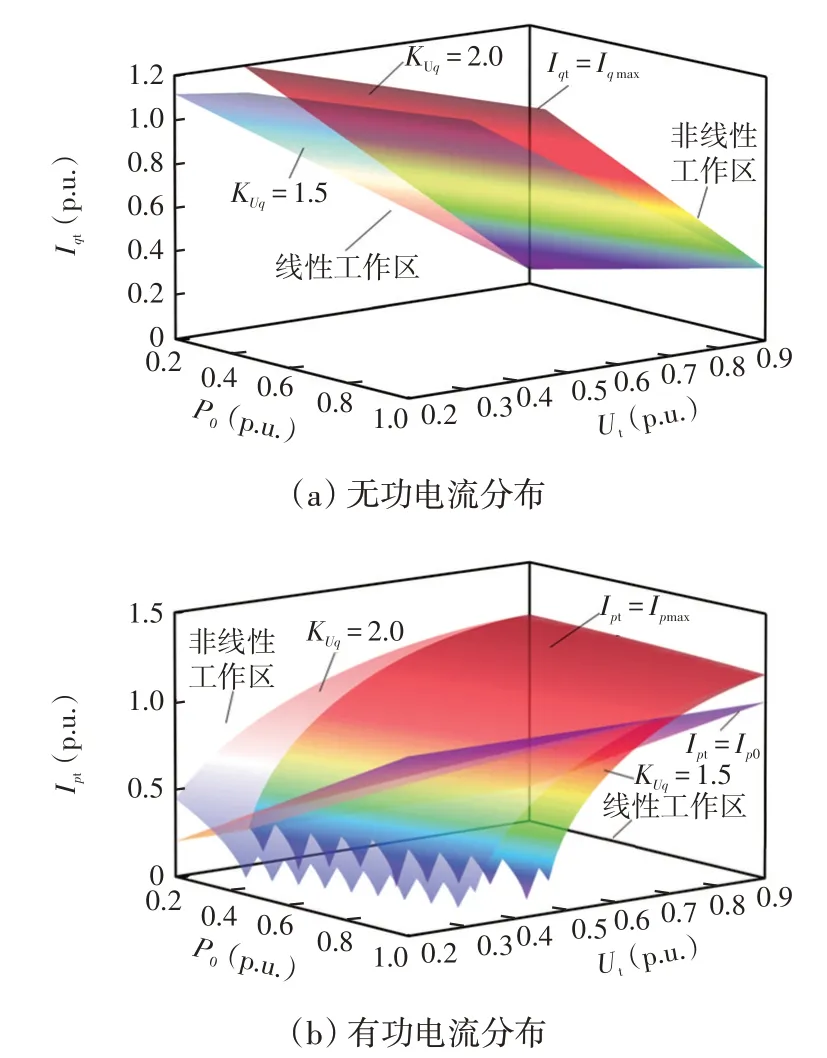
图6 LVRT 工作区划分Fig.6 Workspace division of LVRT

由图6 可知，划分Iqt和Ipt工作区边界条件分别为[0,Iqmax)和[0,Ip0)∩(Ip0,Ipmax)，数据预处理步骤如下。

步骤1选取Iqt未达到Iqmax的工况；

步骤2采用LS拟合获取Iqt控制系数的初值；

步骤3基于Iqt控制系数初值计算出Ipmax；

步骤4选取Ipt分布于线性工作区的工况。

为验证数据预处理后的辨识结果能够全面反映各工况下的LVRT 特性，将辨识结果代入非线性工作区的工况，将仿真结果和测试结果进行对比。

4.3 参数辨识流程

如图7所示为基于LS和ASO算法辨识的原理，图中Iqtfit和Iptfit分别为无功和有功电流计算输出值。

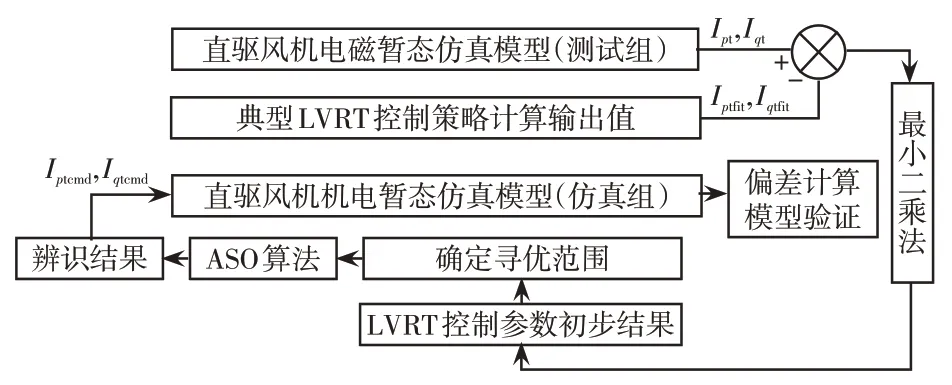
图7 基于LS 和ASO 算法的LVRT 控制参数辨识原理Fig.7 Schematic of identification of LVRT control parameters based on LS and ASO algorithms

由图7 可知辨识原理为：首先基于测试数据，采用最小二乘法拟合得到LVRT控制参数的初步结果，确定寻优范围；然后将测试值和仿真模型输出电流相减，采用合适的目标函数进行评估，得到适应度，利用ASO 算法迭代进行优化；最后将多次辨识结果的平均值代入机电暂态仿真模型，计算仿真和测试结果的偏差，验证模型的有效性。具体过程如下。

步骤1将待辨识工况中的无功和有功电流分别记为Iqt=(Iqt1,Iqt2,…,Iqtn)T，Ipt=(Ipt1,Ipt2,…,Iptn)T，采用最小二乘法拟合[8]得到LVRT控制参数初始值。

步骤2依据LS拟合结果，确定寻优范围。

步骤3设置均匀分布的随机种群为

式中：、和（i=1，2，…，N）分别对应t时刻第i个种群中KUq、KIq和Iqset的取值；、和分别对应t时刻第i个种群中KUp、KIp、Ipset的取值。

步骤4定义目标函数和为

式中：n为工况组数；和分别为无功和有功电流LVRT 控制系数的辨识结果；和的计算结果分别为Iqt和Ipt的适应度；p[Iqt(k)]和p[Ipt(k)]分别为第k组工况Iqt和Ipt的惩罚因子，表示输出值与测试值的误差超出当前误差允许范围的工况组数，组数越多，惩罚因子越大。惩罚因子表达式为

式中：EIqt(k)和EIpt(k)分别为第k组工况Iqt和Ipt的当前误差；countif 为计数函数；εIqt(k)和εIpt(k)分别为Iqt和Ipt当前误差允许范围，设定其初值为0。

步骤5计算种群的初始全局最佳适应度，全局最优位置为食物位置，将种群平均分为雄性和雌性两组，即

分别计算两个种群的初始个体适应度和，位置分别为和；分别计算种群初始最佳适应度和，位置分别为和。

步骤6若t＞T，则参数辨识结束，种群中最佳适应度个体即为无功电流控制系数；否则，转至步骤7。

步骤7依据目标函数进行评价，若满足EIqt(k)＜εIqt(k)，则辨识结束，当前对应的位置即为无功电流LVRT 控制系数；否则，将当前允许误差εIqt和εIpt的初值增加1%，转至步骤8。

步骤8根据式（2）计算Q（t），若Q（t）＜Q_th，根据式（3）更新个体位置；否则，转至步骤9。

步骤9根据式（2）计算T（t），若T（t）＞T_th，转至步骤10；否则，转至步骤11。

步骤10根据式（25）更新种群位置，为当前辨识得到的无功电流LVRT控制系数。

步骤11比较modle和modle_th，若modle＜modle_th，转至步骤12；否则，转至步骤13。

步骤12更新种群位置为

步骤13更新位置为

步骤14判断是否产生新一代个体，若产生，则根据式（10）重新初始化种群。

步骤15比较当前个体和历史个体最佳适应度值，判断是否需要更新适应度。全局最优位置即为无功电流控制系数的辨识结果。

步骤16利用与步骤6～步骤15相同的方法更新种群位置，得到有功电流LVRT控制系数。

图8为直驱风机LVRT控制参数辨识的流程。

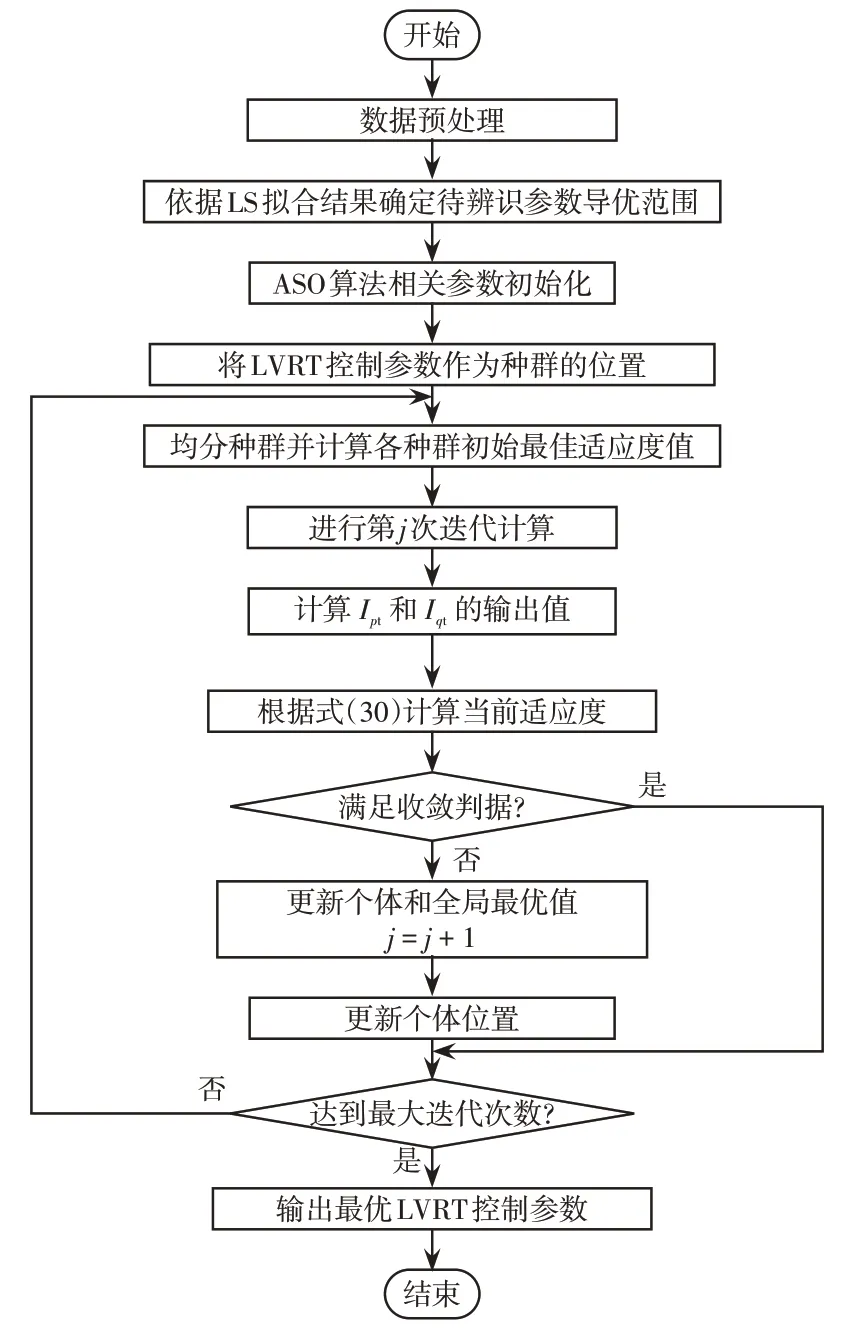
图8 参数辨识流程Fig.8 Flow chart of parameter identification

5 算例仿真

基于PLECS仿真平台搭建1.5 MW直驱风机的电磁暂态模型，主要仿真参数如表4 所示，以电磁暂态仿真结果作为测试结果进行参数辨识，并将辨识结果代入PSASP平台搭建的机电暂态模型，最后将仿真结果与测试结果对比，验证所提辨识方法的有效性。

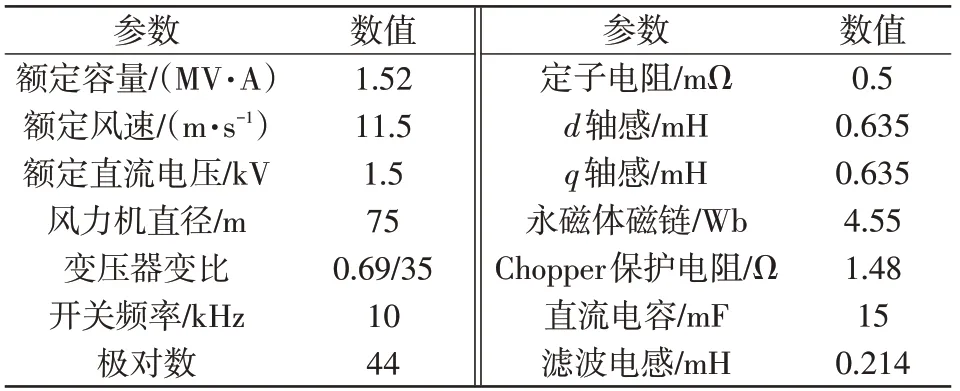
表4 主要仿真参数Tab.4 Main simulation parameters

5.1 ASO 算法有效性验证

将PSO、SO和ASO算法独立运行50次，取其平均值，以降低算法随机性带来的误差影响。设置D=3，N=30，T=200，Q_th=0.25，T_th=0.6，model_th=0.2，c1=0.6，c2max=0.05，c2min=0，c3max=2，c3min=1.8，c4max=c5max=0.6，c4min=c5min=0。

图9 为采用以上3 种算法辨识LVRT 控制参数时的平均最佳适应度曲线，其对比结果见表5，Ipt的最佳适应度最大、最小和平均值分别为fip,max、fip,min和fip,avg，Iqt的最佳适应度最大、最小和平均值分别为fiq,max、fiq,min和fiq,avg。可见，3 种算法多次辨识得到的最优值相同，说明最优解具有唯一性；ASO 算法的平均最佳适应度与最优值相同，而其余两种算法都具有一定的波动，说明ASO算法稳定性更强。辨识无功电流LVRT 控制系数时，ASO算法和SO算法达到全局收敛的迭代次数分别为46次和101 次，辨识有功电流LVRT 控制系数时的迭代次数分别为42次和101次，ASO算法的收敛速度分别提升了54.455%和58.416%。

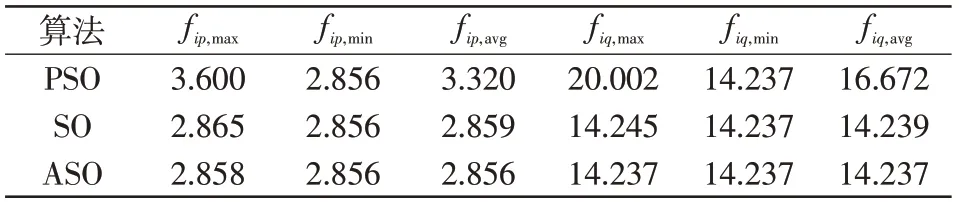
表5 最佳适应度的对比Tab.5 Comparison of best fitness values

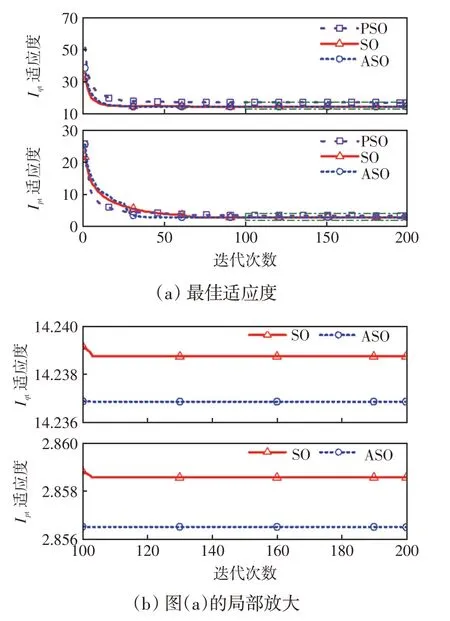
图9 平均最佳适应度曲线Fig.9 Curves of average best fitness

表6 为LS、PSO、SO 和ASO 算法的辨识结果以及最佳适应度的标准差。可见，ASO算法的平均值和标准差均小于PSO算法，SO和ASO算法的平均值虽然相同，但ASO 算法的标准差更小，说明ASO 算法具有更强的稳定性，多次辨识结果的一致性更高。

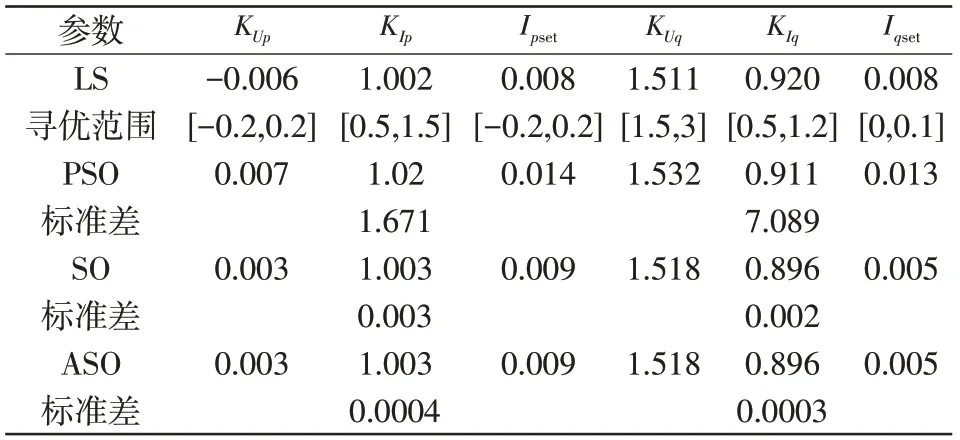
表6 辨识结果对比Tab.6 Comparison of identification results

5.2 ASO 算法适应性验证

对于直驱风机的机电暂态建模，LVRT 控制参数应尽可能适应全部工况，令模型在各工况下均能满足模型验证偏差指标，因此应优先考虑辨识结果对极端工况的适应性。将辨识结果代入不同工况，计算仿真与测试值的误差，并与LS 拟合结果对比。图10为各工况下输出的Ipt和Iqt误差，其中图10（a）和图10（b）分别为PF=0.95 和PF=1.00 下的Ipt误差，图10（c）和图10（d）分别为PF = 0.95 和PF =1.00下的Iqt误差。采用LS和ASO算法产生的Ipt最大误差分别为4.734%和1.945%，Iqt最大误差分别为15.417%和11.971%，可见采用ASO 算法，Ipt和Iqt的最大误差分别降低了58.914%和22.702%，说明ASO算法提高了辨识结果对极端工况的适应性。

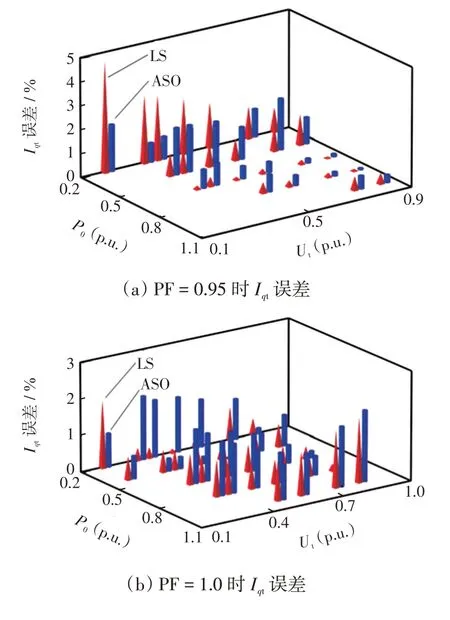
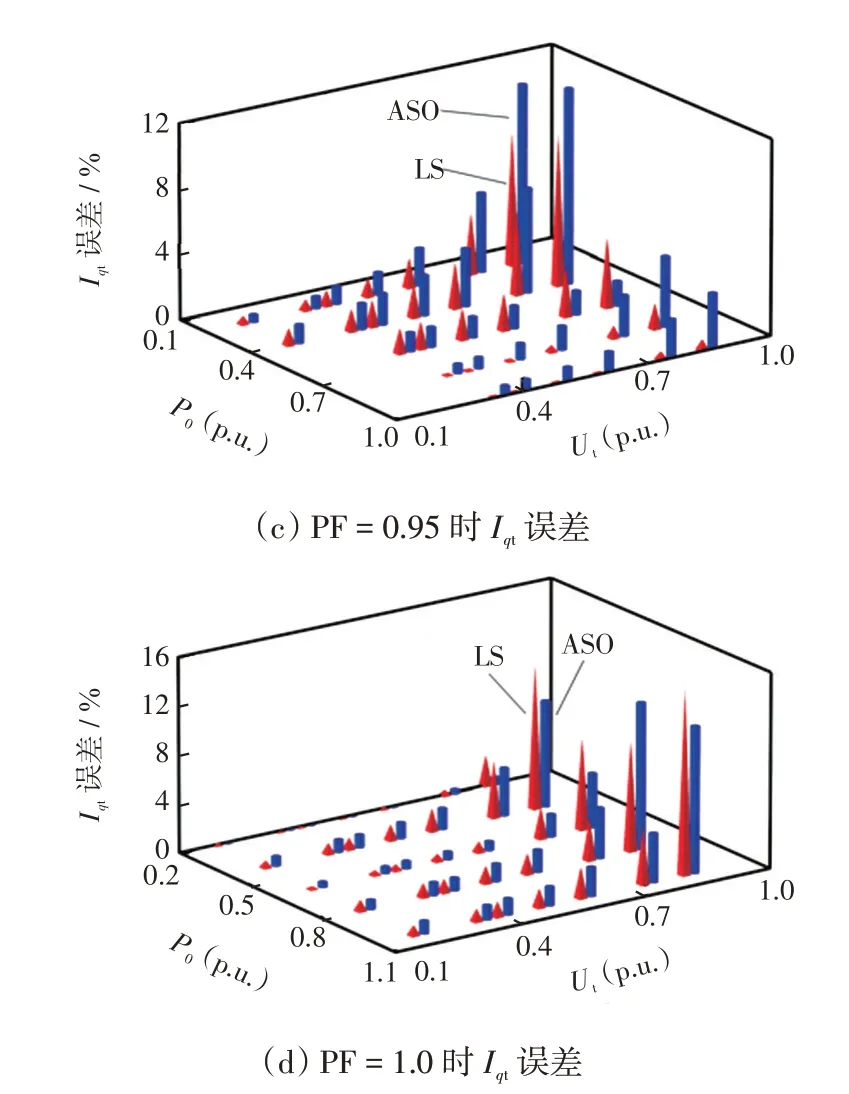
图10 辨识误差Fig.10 Identification error

5.3 偏差计算

本节通过计算模型仿真与测试结果Iq、P和Q的偏差，验证建模准确性。以U为例，t1和t3分别为仿真起始和结束时刻，t2为故障清除时刻，将扰动过程划分为5个区间：A、B1、B2、C1和C2，如图11所示。

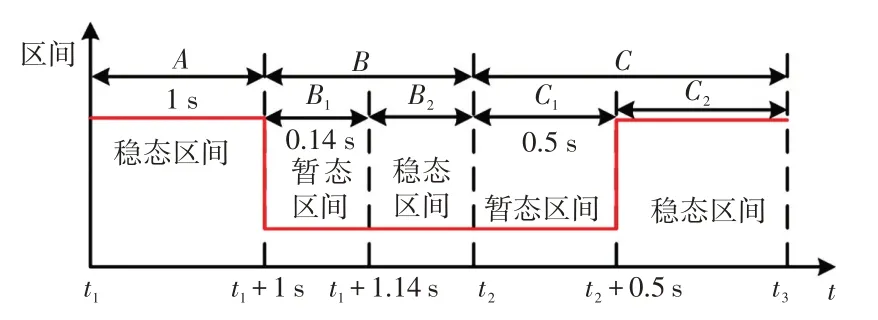
图11 误差计算的5 个分区间示意Fig.11 Schematic of five intervals for error calculation

各区间的偏差计算公式[17]为

式中：xmea和xsim分别为测试值和仿真值；δME和δMAE分别为各区间的平均偏差和平均绝对偏差；δG为加权平均绝对偏差；δMXE为最大偏差的最大允许值；Kstart和Kend分别为起始和结束工况数据的序号。表7为机电暂态模型验证标准[17]规定的最大误差允许值。

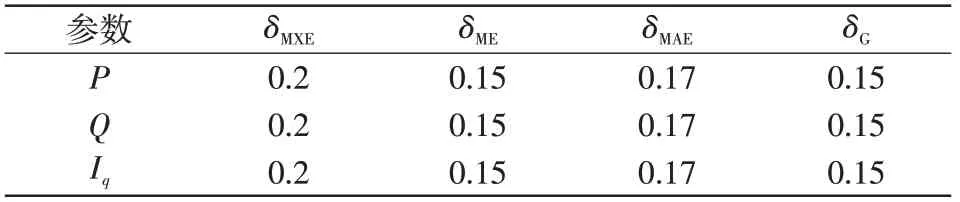
表7 机电暂态模型验证标准规定的偏差最大允许值Tab.7 Allowed maximum deviations in the machineelectricity transient model validation standard

选取包含大功率(P0≥0.9 p.u.)、中功率（0.5 p.u.≤P0≤0.7 p.u.）和小功率（0.1 p.u.≤P0≤0.3 p.u.）的6组工况[4]，如表8 所示，其中PF 为功率因数，计算模型B区间的偏差。若满足表7 规定的范围，则模型有效。

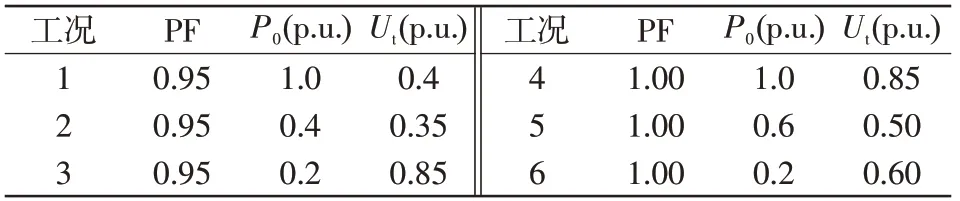
表8 待验证工况Tab.8 Cases to be verified

将LVRT控制参数辨识结果代入机电暂态仿真模型，4 s 时发生三相对称故障，持续0.625 s，仿真获取机端电压U、无功电流Iq、有功功率P和无功功率Q的响应曲线，图12～图17为仿真和测试结果的对比，除工况1外，均为线性工作区工况。

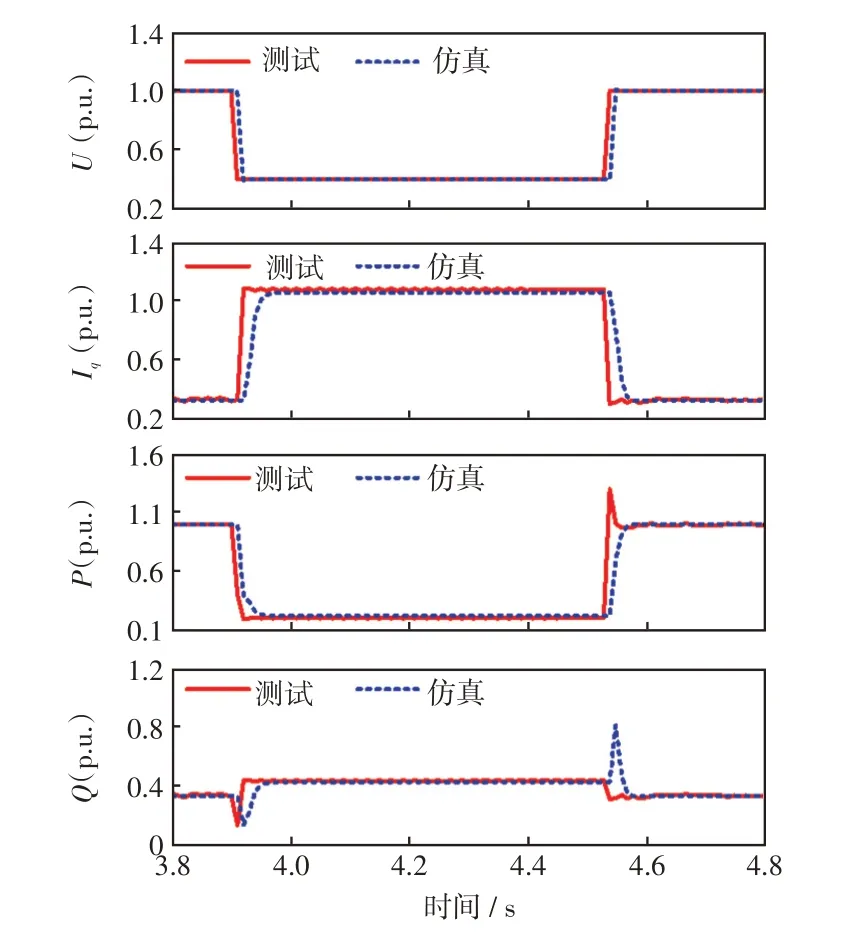
图12 仿真结果与测试结果对比（工况1）Fig.12 Comparison between simulation and test results(Case 1)

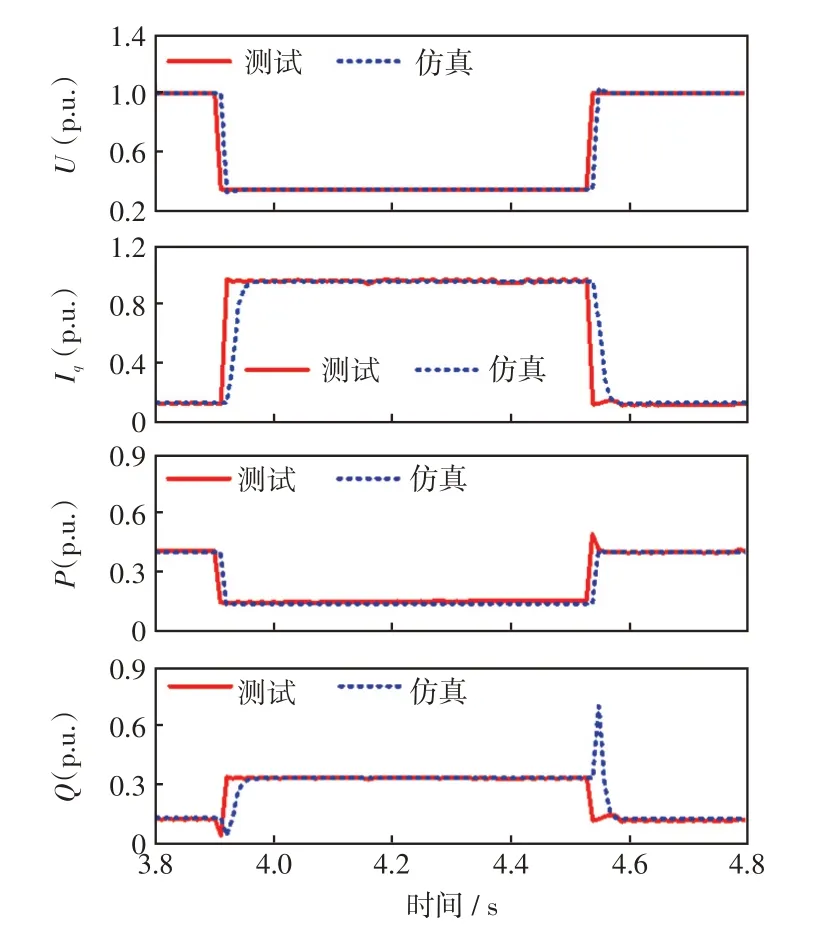
图13 仿真结果与测试结果对比（工况2）Fig.13 Comparison between simulation and test results(Case 2)

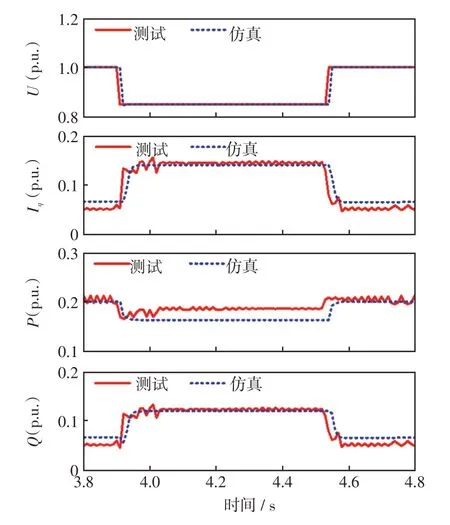
图14 仿真结果与测试结果对比（工况3）Fig.14 Comparison between simulation and test results(Case 3)

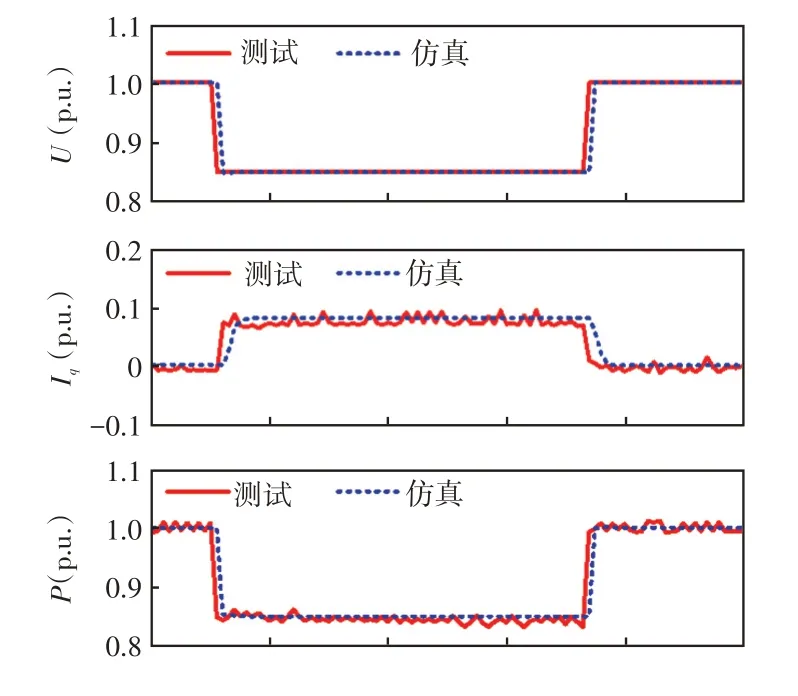
图15 仿真结果与测试结果对比（工况4）Fig.15 Comparison between simulation and test results(Case 4)

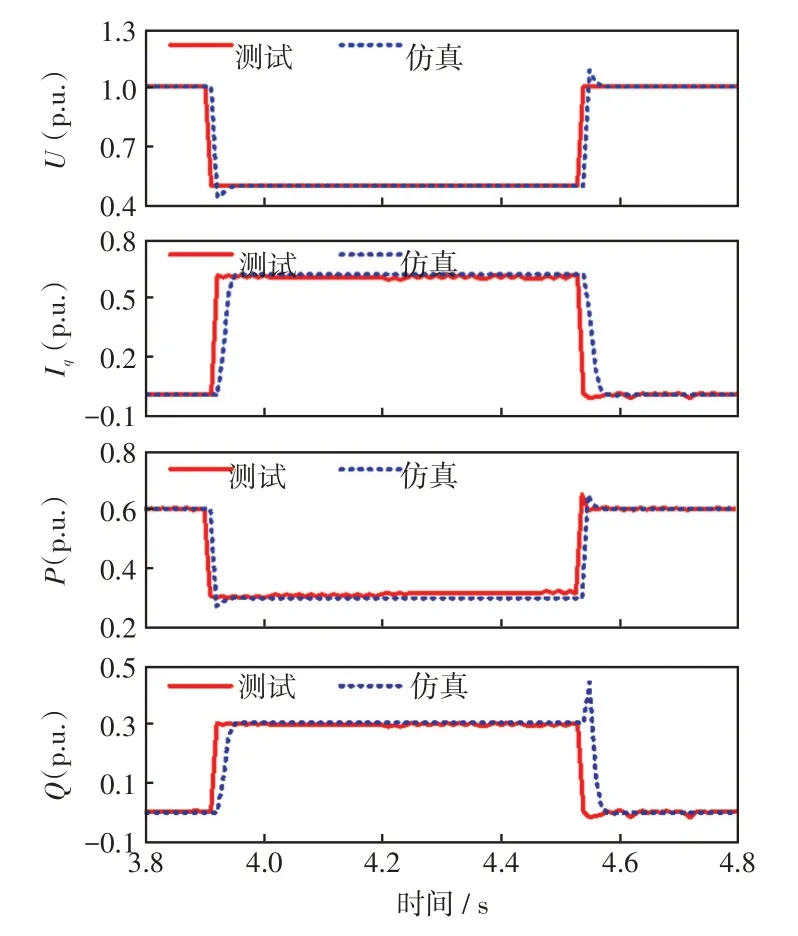
图16 仿真结果与测试结果对比（工况5）Fig.16 Comparison between simulation and test results(Case 5)

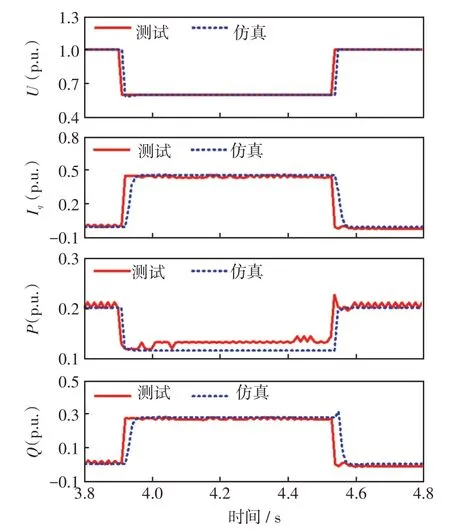
图17 仿真结果与测试结果对比（工况6）Fig.17 Comparison between simulation and test results(Case 6)

对6 组工况下B 区间各电气量的偏差进行计算，结果如表9～表14所示，可见各工况下的偏差均小于表7中规定的偏差最大允许值。此外，仿真结果表明，辨识结果对非线性工作区工况也具有良好的适应性。

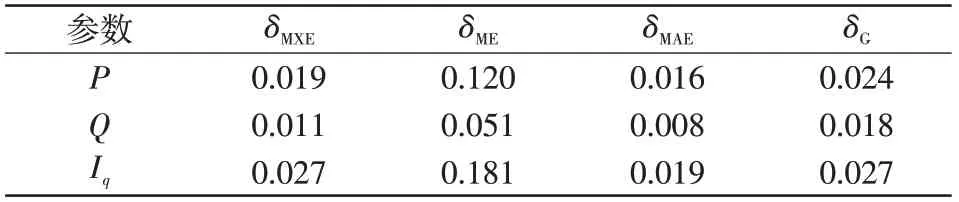
表9 仿真模型偏差（工况1）Tab.9 Deviations of simulation model(Case 1)

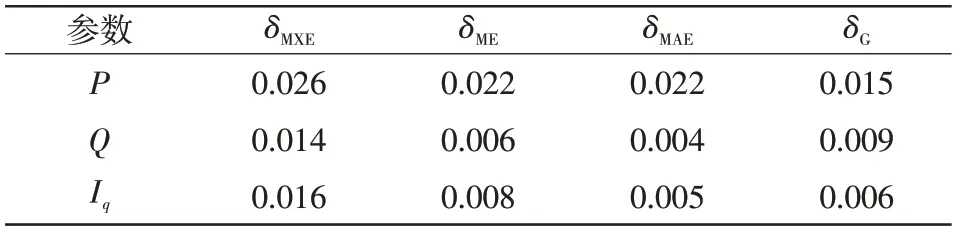
表11 仿真模型偏差（工况3）Tab.11 Deviations of simulation model(Case 3)

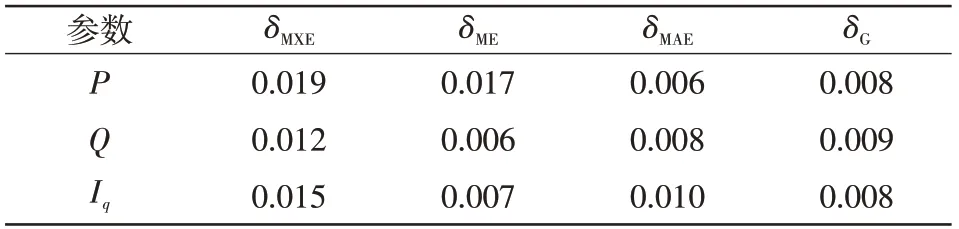
表12 仿真模型偏差（工况4）Tab.12 Deviations of simulation model(Case 4)

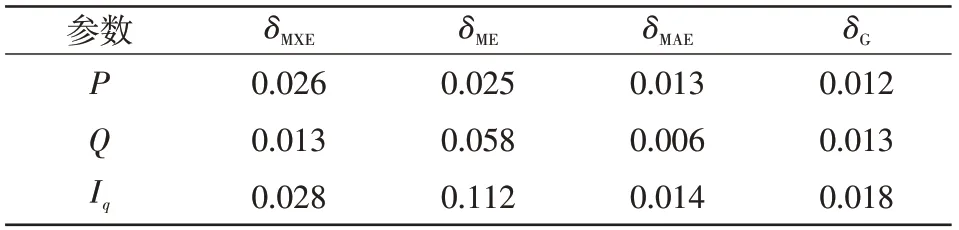
表13 仿真模型偏差（工况5）Tab.13 Deviations of simulation model(Case 5)

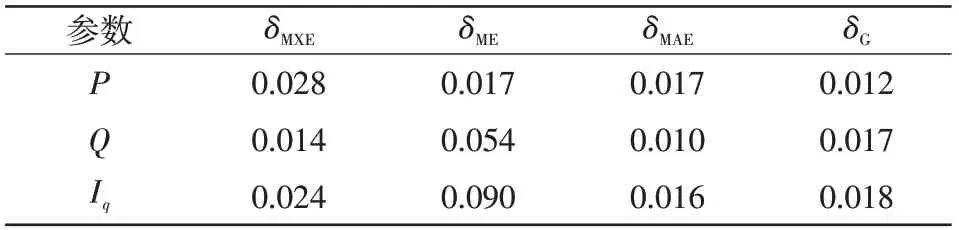
表14 仿真模型偏差（工况6）Tab.14 Deviations of simulation model(Case 6)

6 结 论

针对传统LVRT 控制参数辨识方法辨识精度低、对极端工况适应性差以及多次辨识结果一致性较低的问题，本文提出了一种基于LS 和ASO 算法的直驱风机LVRT 特性辨识方法。该方法能够准确、快速地辨识出直驱风机LVRT控制参数，所得结论如下。

（1）利用LS 拟合能够为ASO 算法提供待辨识参数寻优范围，减小了初值对寻优精度产生的误差影响。

（2）对6种基准函数的测试结果表明，ASO算法通过引入Levy飞行策略和自适应学习因子设计，保证了种群多样性和收敛速度，寻优效果优于SO算法。

（3）采用PSO、SO 和ASO3 种算法进行50 次参数辨识的结果表明，ASO 算法的稳定性最强，平均最佳适应度和标准差均小于PSO 和SO 算法。另外，相比SO算法，ASO算法辨识有功电流和无功电流控制系数时的收敛速度分别提升了54.455%和58.416%。

（4）ASO算法的辨识结果对极端工况具有更好的适应性，相比最小二乘法的拟合结果，在极端工况下，有功电流和无功电流误差分别降低了58.914%和22.702%。