含新能源和电动汽车充电站并网的主动配电网无功优化模型

江智军，袁 轩，邱文浩，黄礼才，何 伟

（1.南昌大学信息工程学院，南昌 330000；2.国网江西省电力科学研究院，南昌 330000）

电动汽车和新能源技术的快速发展，对我国缓解能源危机、实现“双碳”目标起了重要作用[1-2]。但是，随着以光伏、风电为主的新能源和电动汽车渗透率地不断提升，一些新的问题也随之产生。首先，新能源并网会改变原系统的潮流分布，造成配电网电压越限，加大了有功损耗，降低了系统可靠性[3]。其次，由新能源发电量增加和光伏发电站无惯性特征引起的系统功率平衡问题，以及新能源随机出力特性造成的电压波动问题给系统的稳定性带了来严重威胁[4-6]。再次，电动汽车的特殊负荷特性使得系统的稳定性进一步降低[7-8]。因此，合理地改进无功优化模型，动态地改善系统无功潮流分布，对降低功率传输过程中的有功损耗、改善系统电压水平和提升系统稳定性具有重要意义[9-11]。

目前，国内外学者在配电网无功优化方面做了比较全面的研究，其中在无功调节措施方面，由于逆变器的存在，使得风力发电机组和光伏电站具有无功调节能力而被广泛应用于无功优化之中。文献[12]将光伏逆变器作为无功源，建立了考虑光伏逆变器无功调节能力的配电网无功优化模型，利用线性递减权重粒子群算法实现无功补偿装置的最优配置；文献[13]着重对双馈风力发电机的容量曲线进行分析建模，在其无功出力特性的基础上建立了具有分布鲁棒特性的两阶段无功优化。随着研究的进一步深入，已经有部分研究人员开始重视充电机的无功调节作用[14-15]。文献[16]综合运营商和用户的双方利益，以充电机的功率因素角作为优化变量，建立了配用电系统综合无功优化模型；文献[17]考虑到充电机与电网间的功率双向交互能力和充电负荷的时空分布特性，建立了双层模型对充电站的有功无功进行分层优化调度，另外可投切电容器组CB（capacitor bank）由于调节速度慢、不能频繁动作的缺点使其无法满足系统的动态调节要求；对此，文献[18]采用二阶锥松弛技术，将含有无功调节设备动作次数约束的无功优化问题转化为混合整数的二阶锥问题，然后采用商业求解器求解，这种方法具有充分的理论依据，求解精度高，但是难以求解含非凸目标函数的无功优化问题；文献[19]将电容器组的动作次数约束松弛处理，再进行静态无功优化，根据优化结果制定动作时刻表，这种方法对于时段的划分仅依靠电容器组投入结果，虽然能满足动作次数约束，但不能保证其动作时刻的合理性；文献[20-21]将CB动作成本作为目标函数，以此降低CB的动作次数；不仅如此，考虑除常规无功补偿装置外的新能源无功调节能力，模型变量具有多样化的特征，文献[22]采用改进鲸鱼算法对含多种变量类型的无功优化模型进行求解，虽然在一定程度上提升了全局优化能力，但对于离散型变量依然是简单的取整操作，降低了求解效率；文献[23]采用分解协调法，将原问题分解为仅含离散型变量或连续型变量的子问题，分别采用不同算法进行协调求解，这种方法虽然降低了求解难度，但是将离散型变量和连续型变量独立求解会导致搜索路径发生偏移，难以得到原问题的最优解。上述文献虽然通过改进无功优化模型或优化算法在一定程度上解决了新能源并网引起的电压波动和网损问题，但是均忽略了电动汽车充电站接入负荷侧带来的影响，并且对于负荷侧和电源侧引起的稳定性问题没有足够的重视。

针对上述研究的不足，本文建立了含新能源和电动汽车充电站并网的主动配电网无功优化模型，提出一种新的评判系统稳定程度的静态电压稳定性指标，同时，根据不同决策变量特征，将改进飞蛾扑火算法与遗传算法组合形成具有交叉反馈机理的混合优化算法，对离散型变量和连续型变量区别求解，进而提升求解的准确性和快速性。

1 新能源和电动汽车随机模型

风电、光伏和电动汽车的接入是引起主动配网电压波动的主要原因，对其出力进行准确且合理的预测是无功优化的前提。

1.1 风力发电随机模型

本文对双馈感应发电机DFIG（doubly-fed induction generator）的出力特性进行分析。风力发电机的有功输出主要受风速影响，短期内风速变化主要服从高斯分布[24]，其概率密度函数为

式中：f(v)为概率密度；σ、μ和v分别为标准差、期望和风速。风机出力与风速之间的函数关系为

式中：PWT、Pr分别为风力发电机的实际有功输出和额定功率；vaw、vr、vci和vco分别为机组的实际风速、额定风速、切入风速和切出风速。

换流器的存在使得DFIG 的定、转子同时具有无功调节的功能[25]。根据文献[26]所述标准，风力发电机组应满足功率因数在-0.95～0.95范围内可动态调节。

1.2 光伏发电随机模型

光伏出力受太阳辐射强度影响呈正相关，具体关系为

式中：PPV为光伏出力L为太阳辐射强度；S和λ分别为太阳能电池片触光面积和光电转换效率。

短期内，太阳能辐射强度满足Beta分布[27]，即

式中：Lmax为太阳辐射强度的最大值；α和β分别为形状参数和尺寸参数。

光伏逆变器使得光伏电池具有无功调节的功能，其无功调节极限为

式中：QPV,max、QPV,min分别为光伏电站无功输出最大、最小值；Sgv,max为光伏逆变器的容量，一般为额定容量PPV,max的1.1倍。

1.3 电动汽车随机模型

以电动私家车为例，其日行驶里程s和起始充电t时刻满足概率密度函数[28]，即

式中：μD和σD分别为日行驶里程的期望值和标准差，分别取3.20 和0.88；μT和σT分别为起始充电时刻的的期望值和标准差，分别取17.6和3.4。

电动汽车充电时长可估计为

式中：TC为充电时长，h；W100为百公里耗电量，kW·h/km；PC为充电功率，kW。

用蒙特卡洛法对电动汽车充电站的充电功率进行模拟分析，其充电功率PEV,t可以表示为

式中：Nc为电动汽车总数；PCn,t为t时段电动汽车n的充电功率。

2 多目标无功优化数学模型

无功优化的目的是在配电网现有拓扑结构以及各类无功补偿装置的基础上，通过调整新能源以及各种无功补偿装置的出力，使得主动配电网的一类指标或者多类指标能够达到最优。

2.1 目标函数

（1）系统运行成本f1最小，表示为

式中：N为节点总数；Yij为支路导纳；Pij,t、Qij,t分别为t时段从支路ij首端流出的有功、无功功率；Uij,t为t时刻支路ij的首端电压；ϕi为连接节点i的节点集合；real()为取实部操作；η为电容器组的动作成本，取1.6 元/次[29]；nj,t为t时段节点j处电容器组投切组数；pt为t时段电价。

（2）电压偏移量f2最小，表示为

式中，Ui,t、Ui,max、Ui,min和Ur依次为t时段节点i的电压幅值、电压上、下限和额定电压。

（3）系统稳定性f3最优。为衡量新能源和电动汽车充电站接入前后配电网的稳定性水平，本文提出一种新的电压稳定性指标VSI（voltage stability index）。配电网的电压等级较低，可以忽略线路对地导纳，由此得t时段的单条支路等效模型，如图1所示。

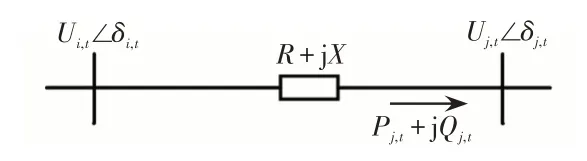
图1 单条支路等效模型Fig.1 Equivalent model of single branch

根据线路潮流方程，得

式中：Uj,t为t时段节点j的电压幅值；δi,t、δj,t分别为t时段支路ij首末端电压相角；δt为t时段首末端电压相角差；R、X分别为支路电阻和电抗；Z为支路阻抗，；Pj,t、Qj,t分别为t时段注入末端节点的有功、无功功率；Sj,t为t时段的视在功率，；Uj1,t、Uj2,t分别为t时段如图2所示PV曲线的上半支和下半支电压解。

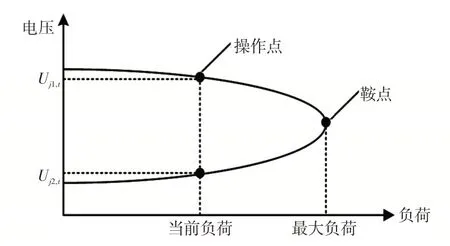
图2 PV 曲线Fig.2 PV curve

由于电力系统支路首末端电压相角差很小，可设δt≈0，则有cosδt≈1，联立式（12）～式（14）得

在系统逐渐临近崩溃点时，Uj1,t-Uj2,t逐渐趋于0，当系统稳定运行直至临近崩溃时，可得t时段支路ij的电压稳定性指标为

当Lij,t≥1 时，主动配电网系统的电压则会出现剧烈波动，最终崩溃。由于任何支路的电压崩溃均会导致整个系统不稳定，因而将所有支路电压稳定性指标的最大值作为t时段系统的电压稳定性指标Ldet,t，即有

式中，S为系统支路集合。为使系统稳定性更强，定义目标函数f3为

2.2 约束条件

（1）功率平衡约束表示为

式中：PGRID,t为大电网t时段注入系统的有功功率；PWT,j,t、PPV,j,t分别为t时段注入节点j的风电和光伏的有功功率；PLOAD,j,t、PEV,j,t、PLOSS,j,t分别为t时段在节点j消耗的负荷的有功功率、电动汽车充电站的充电功率和系统有功损耗；QGRID,t为大电网t时段注入系统的无功功率；QWT,j,t、QPV,j,t、QCB,j,t、QSVC,j,t分别为t时段注入节点j的风电、光伏的无功功率、电容器组的无功功率和静止无功补偿装置的无功功率；QLOAD,j,t、QLOSS,j,t分别为t时段在节点j处负荷的无功功率和系统无功损耗；πWT、πPV、πCB、πEV、πSVC分别为安装风机、光伏、可投切电容器组、电动汽车充电站和静止无功补偿装置的节点集合；πSUM为系统负荷节点集合。

（2）电压电流约束表示为

式中：Iij,max、Iij,min分别为流过支路ij的电流上、下限；Ui,max、Ui,min分别为节点i的电压幅值上、下限。

（3）控制变量约束表示为

式中：、分别为t时段节点j的风机无功功率上、下限；、分别为t时段节点j的光伏无功功率上、下限；、分别为t时段节点j的可投切电容器组无功功率上、下限；、分别为t时段节点j的静止无功补偿装置无功功率上、下限。

（4）电动汽车充电站功率约束表示为

式中：PEVS,j,t为t时段电动汽车充电站在节点j所耗有功功率；、分别为其上、下限；QEVS,j,t和、分别为t时段电动汽车充电站在节点j注入的无功功率及其上、下限；SEVS,j,t为t时段节点j的充电站容量。

（5）CB动作次数约束表示为

式中，nc为日最大可投切次数，取值为6[30]。

2.3 多目标归一化

量纲不同的目标函数之间存在冲突和制约，优化后的各项指标难以同时获得最优。因此，采用极差标准法对子函数进行无量纲化，其表达式为

式中：yij为无量纲化的函数数据；xij为评价对象i指标j的数值；分别为所有评价对象i指标j的最大值和最小值；m、n分别为评价对象i和指标j的个数。

对子目标进行无量纲化后，依据有功网损大于电压偏移、电压偏移大于电压稳定性的重要程度，采用层次分析法[31]把多个目标函数统一为

式中：wj为指标j的权重系数，经计算分别取为w1=0.637，w1=0.258，w3=0.105；fj*为无量纲化后指标j的数值。

3 交叉反馈混合优化算法

主动配电网的日前无功优化问题属于大规模优化问题，涉及到的决策变量数目庞大，而本文在投入传统无功补偿装置的基础上进一步考虑了新能源、电动汽车充电站的无功补偿作用，这使决策变量更加多样、复杂。对此，本文提出基于改进飞蛾扑火算法与遗传算法组合，形成具有交叉反馈机理的混合优化算法对本文所提模型进行求解，将连续型变量和离散型变量进行区别求解，而后将优化结果相互反馈，不仅降低了决策变量维度，还有效结合了不同优化算法针对性处理不同决策变量类型的特点，使得算法的优化时间和全局搜索能力得到了极大的提高。

3.1 改进飞蛾扑火算法

飞蛾扑火MFO（moth flame optimization）算法[32]利用飞蛾夜间飞行导航机制产生新的种群，原理简单，易于编程，但MFO 算法在初始化种群和寻优后期种群多样性低，易陷入局部最优。对此，本文对MFO算法加以改进，提出一种基于Tent混沌映射和自适应变异算子的改进飞蛾扑火算法TAMMFO（moth flame optimization algorithm based on Tent chaotic mapping and an adaptive mutation operator），具体步骤如下。

（1）加入Tent混沌映射增加初始解的多样性，其表达式为

式中：ym为第m次产生的混沌变量；α为0.5[33]。

将混沌变量y映射到解空间为

式中：xmax、xmin分别为变量上、下限；Y为映射到解空间后的量。

（2）引入基于种群聚集度的自适应变异算子，增强种群的多样性。种群聚集度C定义为

式中：D为个体维度；NP为个体数；Xi,k为个体i的第k维位置；为种群在k维位置的平均值。

种群聚集度C体现了飞蛾间的拥挤程度，C越大，说明飞蛾个体分散，种群多样性丰富；反之，说明个体差异性小，算法易陷入局部最优，导致早熟。基于式（29），引入种群聚集度的自适应变异算子可以表示为

式中：φ、π分别为传统变异算子和异维学习变异算子；Hi,j为个体i的维度j经自适应变异之后的位置；F∈[0,1] 为放缩因子；Xbest,j为种群在第j维的最优位置；i,r1～r5为[1,NP]上的随机数，且互不相等；j为个体维度，j∈[1,D]；K为采用随机广义方式选择的异维维度，K∈[1,D]且K≠j，具体参见文献[34]。

（3）加入基于聚集度的自适应变异算子策略后，经过螺旋函数更新位置后的部分飞蛾个体进行交叉选择操作，有

式中：为第t次迭代个体i的维度j交叉后的位置；为第t次迭代个体i的第j维位置；Mit为第t次迭代后个体i交叉后的位置；Xit为第t次迭代后个体i的位置；CR为交叉概率；fit()为求取适应度函数。

3.2 混合优化算法

多种群交叉反馈算法针对不同类型变量采用不同种群反馈的信息进行寻优。本文中，SVC、新能源和电动汽车充电站无功出力为连续型变量，CB投切组数为离散型变量，分别采用TAMMFO 和遗传算法GA（genetic algorithm）对不同类型变量进行交叉反馈优化。在寻优过程中，不同种群的寻优过程相互独立，并将最终寻优结果共享。

对于连续型变量采用TAMMFO 算法，对离散型变量采用GA 算法求解，遗传算法基于生物进化理论启发而来，通过选择、交叉、变异3 种操作寻优，在求解复杂非线性整数优化问题中有明显优势。混合种群的交叉反馈表现为用不同算法交叉独立求解整个问题，在初始阶段采用Tent混沌映射产生初始种群［X，Y］，种群X为离散型变量，在种群Y不变的情况下采用GA算法对种群X进行优化，种群Y为连续型变量，在种群X优化结果的基础上采用TAMMFO算法对种群Y进行优化，然后再在种群Y寻优结果的基础上对种群X进行优化，如此交叉反馈进行优化，直至满足终止条件。采用不同优化算法求解一个问题中的不同类型变量，既综合不同算法的优点，又降低了变量维度，在求解混合整数的复杂非凸、非线性优化问题上具有一定的优越性。算法流程如图3所示。

图3 算法流程Fig.3 Flow chart of algorithm

4 算例分析

以软件Matlab2016a 对如图4 所示的改进IEEE33 节点系统进行分析，其计算机型号为11th Gen Intel（R）Core（TM）i5-11400H@2.70GHz，操作系统为Windows 10 家庭中文版。设系统的基准容量为10 MW，电压等级取12.66 kV；电容器组接入节点9 和32，每组100 kvar，共10 组；SVC 接入节点16、24、30，容量均为800 kvar；风力发电机WT（wind turbine）接入节点25、33，容量均为600 kW；光伏PV（photovoltaic）发电站接入节点18，容量为500 kW；电动汽车充电站采用集中式变流器并入节点12、22，最大容量为0.8 MV·A[17]。图5 为次日风电和光伏有功出力的预测值。

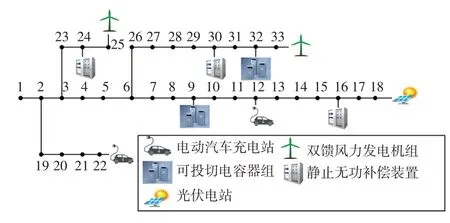
图4 修改过的IEEE33 节点系统示意Fig.4 Schematic of modified IEEE 33-node system

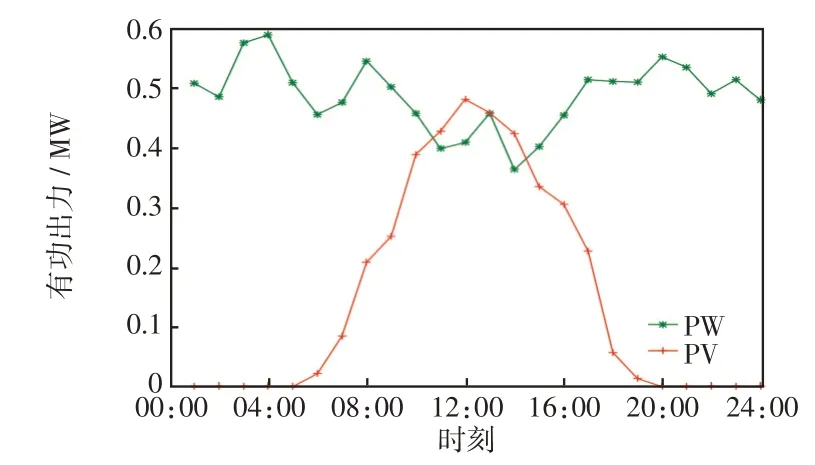
图5 风电和光伏功率预测曲线Fig.5 Forecasting curves of wind and photovoltaic power

设置TAMMFO 算法和MFO 算法种群规模为N=100，对数螺旋旋转常数b=1，自适应变异的飞蛾数为种群的20%，交叉概率为0.9，放缩因子取0.5，最大迭代次数tmax=30，交叉反馈最大迭代次数Tmax=100，遗传算法参数见文献[35]。

假设电动私家车、电动公务车和电动出租车的总数为400 辆，占比依次为0.77、0.10、0.13，具体参数见文献[36]。充电负荷预测值如图6所示，图7给出了次日每小时负荷、包含电动汽车充电负荷在内的总负荷和分时电价。

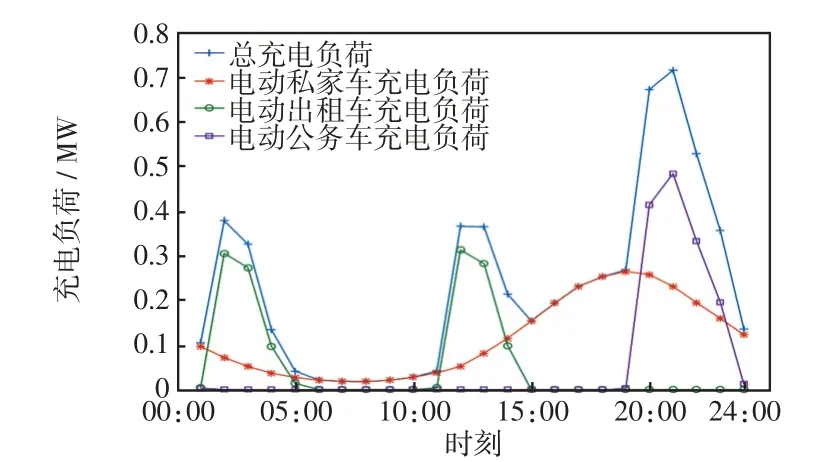
图6 电动汽车充电负荷Fig.6 Electric vehicle charging load

图7 分时电价和负荷曲线Fig.7 Time-of-use electricity price and load curve

为验证交叉反馈混合优化算法的优势，基于以上参数设置2个案例：案例1为TAMMFO算法和GA算法的组合，案例2为MFO算法和GA算法的组合，分别采用不同优化算法组合对模型进行求解，其收敛特性曲线以及对比结果分别见图8和表1。

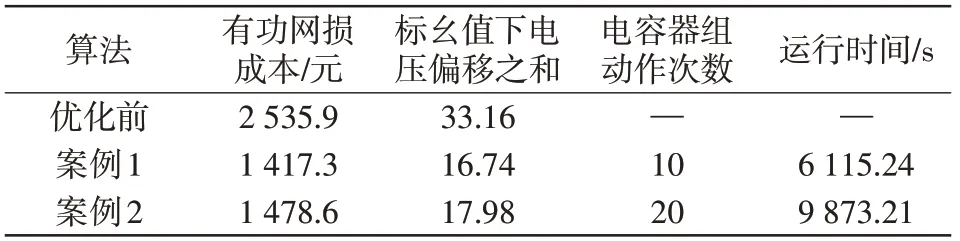
表1 两种算法结果对比Tab.1 Comparison of result between two algorithms

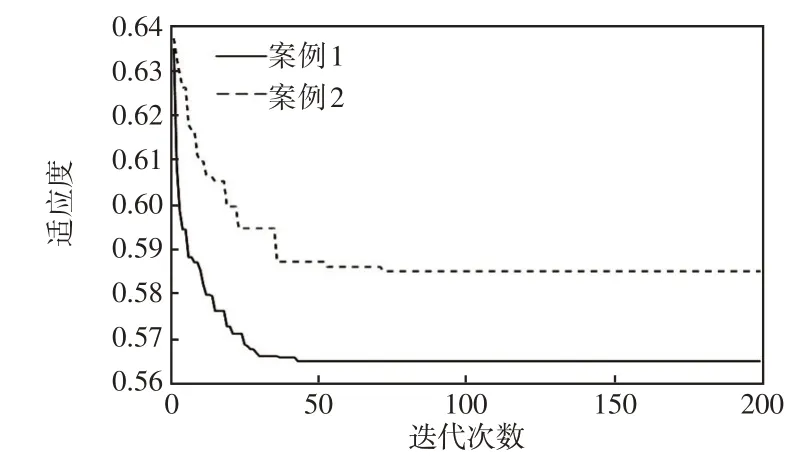
图8 适应度曲线对比Fig.8 Comparison of fitness curve

图8表明，MFO算法在迭代后期易陷入局部最优，主要原因是后期种群多样性较低。由于加入了基于种群聚集度的自适应变异算子，TAMMFO算法在迭代后期能够保持优良的种群多样性，全局搜索能力较强，降低了陷入局部最优的可能。

表1 给出不同算法在优化前后各项指标情况。可知，经过优化后系统的各项指标较优化前均有所提高，案例1的优化效果较案例2的更为明显；案例2 的网损成本、电压偏移较优化前分别减少41.69%、45.78%；较之案例2，案例1 在网损成本上继续减少2.41%，电压偏移上减少3.74%；电容器动作次数方面，案例1的总动作次数为10，较案例2减少了10 次；运行时间上，案例1 较案例2 降低了38.06%，所以案例1代表的本文交叉反馈混合算法寻优效果更好，且寻优速度更快。

优化前后不同案例24 h 网损、电压偏移度和VSI 对比如图9 所示。由图9 可见，用电高峰期间，即21：00 左右，优化前系统有功损耗最高可到375.53 kW 左右。在采取无功补偿措施后，案例1优化后的有功损耗可减少至254.07 kW 左右，较案例2 多减少3.99%。同一时刻，系统电压偏移量为2.32，经过案例1所提算法优化后，电压偏移量降低为1.50，较案例2 多降低2.67%。在优化前，系统VSI最大值出现在22时段，为0.380左右；最小值出现在05：00时刻，为0.240左右。案例1优化策略的投入运行，峰谷VSI 降低为0.367 和0.232 左右，较案例2的分别多降低2.06%和2.03%。

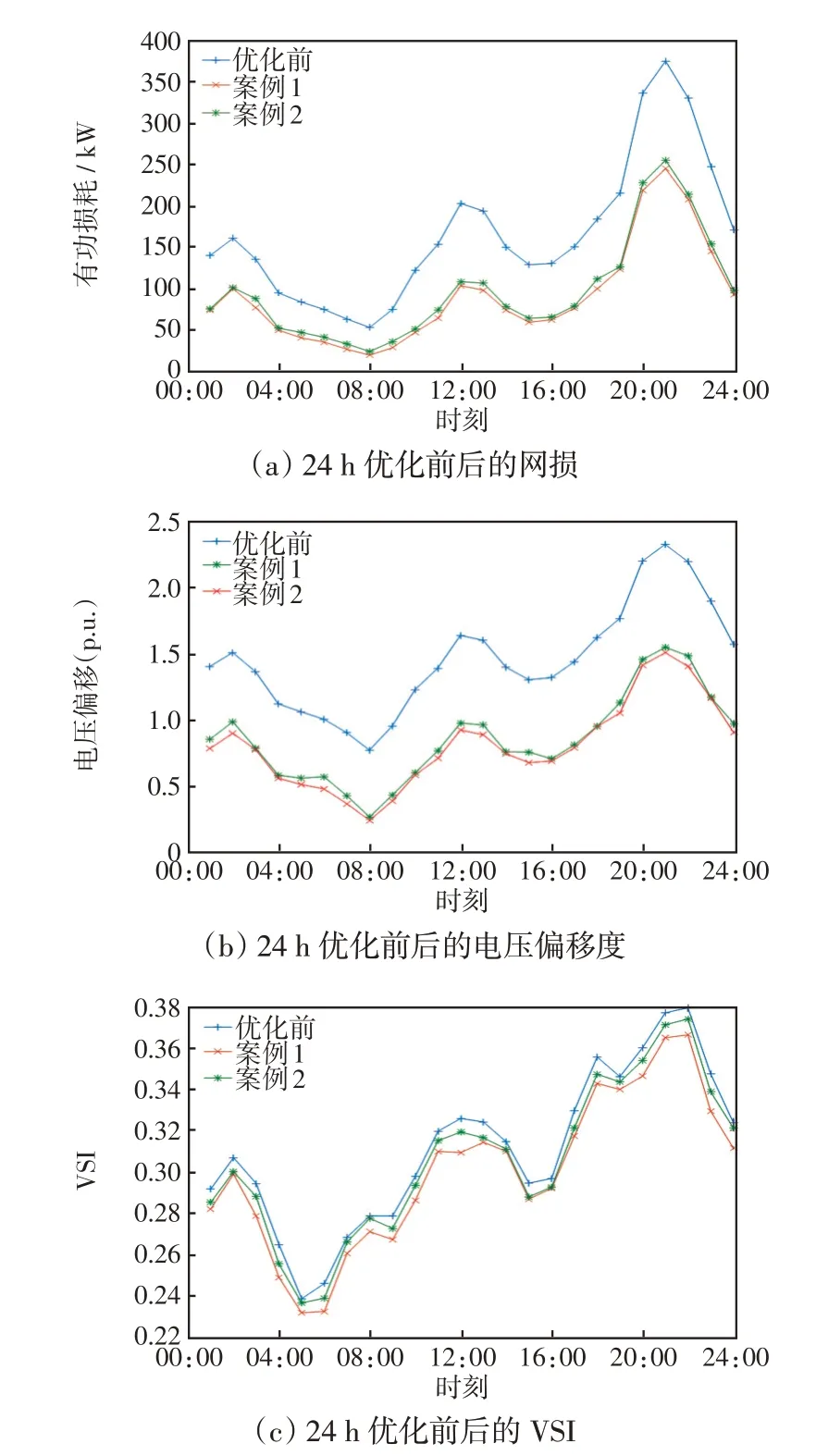
图9 优化前后的结果对比Fig.9 Comparison of results before and after optimization

取全天最大负荷的时刻对系统电压进行分析。在该时刻，分别输出无功优化前后的节点电压，对比结果如图10所示。

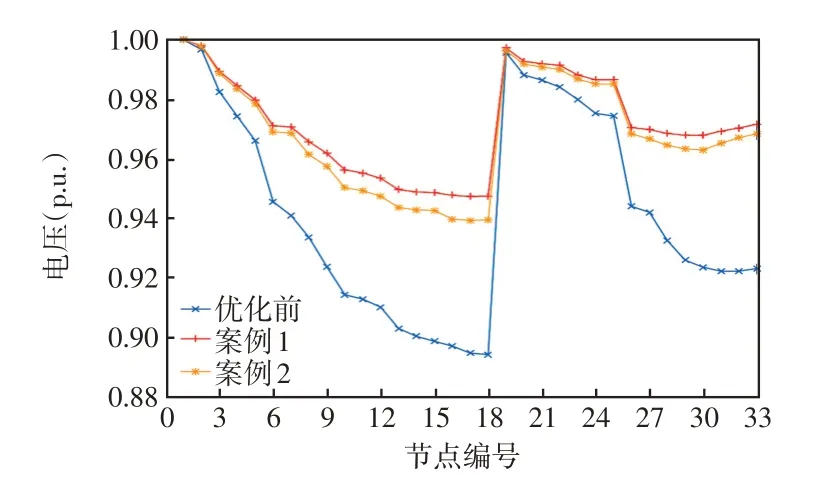
图10 节点电压对比曲线Fig.10 Curves of comparison of node voltage

根据图10 可知，系统未采取无功调节措施时，系统电压在节点18 处最低，达到0.89 p.u.左右。随着优化策略的投入运行，经过案例1优化后系统节点18 的电压抬升至0.95 p.u.，较案例2 的高出0.84%，两种案例的电压水平均达到了系统允许的电压标准，即0.93～1.07 p.u.。

进一步分析本文模型下两种案例电容器组的动作情况，仿真结果如图11 所示，分别对应案例1和案例2 在配电网系统节点9、32 安装的无功补偿电容器在日前不同规划时段的投切调度方案。

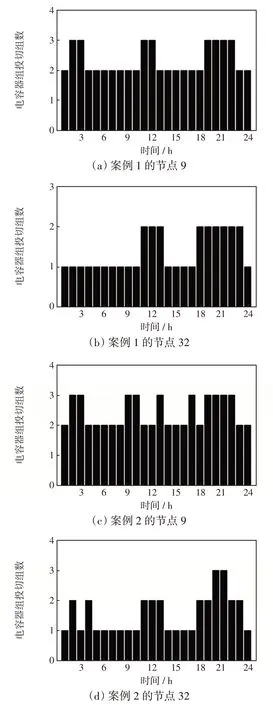
图11 不同案例下电容器动作情况Fig.11 Capacitor action in different cases

由图11可见，案例2中节点9与节点32处所设有的无功补偿装置均动作了10 次，无功容量投切频繁，且均已超过日最高投切次数的限制；案例1中节点9 与节点32 处所设有的无功补偿装置分别动作了6次与4次，相较案例2，动作次数明显降低，电容器的投切次数均在限制范围内。

结合图9～图11 所获得的仿真结果可以看出，案例1 所代表的改进飞蛾扑火算法与遗传算法相结合的优化策略能够更好地提高主动配电网运行的稳定性和经济性。同时，采用改进优化调度方案后，配网节点电压分布更为均匀平缓，从而改善了系统的电压水平，并且本文所提算法能够更好地限制无功调节设备的动作次数，相应地节约了设备动作费用，避免了不必要的设备损耗。

5 结 语

本文考虑新能源和电动汽车充电负荷的动态变化，建立了含新能源和电动汽车充电站并网的主动配电网无功优化模型。根据算例分析结果，得出以下结论。

（1）本文所提主动配电网无功优化模型能够使电压波动更小，稳定性更佳，且系统运行成本进一步降低，因此该模型更适合实际的需求。

（2）针对新能源和电动汽车充电站并网引起的电压波动问题，本文提出了一种新的电压稳定性指标，用于评价系统的稳定性状态。

（3）针对决策变量特征，采用基于改进飞蛾扑火算法和遗传算法的交叉反馈混合算法进行模型求解，结果表明，所提算法收敛速度快、全局搜索能力强，说明该算法可有效求解配电网中具有混合整数的非凸、非线性无功优化问题。