改进黑猩猩算法的光伏发电功率短期预测

谢国民，陈天香

（辽宁工程技术大学电气与控制工程学院，葫芦岛 125105）

作为清洁能源的一种，光伏发电具有十分广阔的应用前景[1-3]，但大规模接入电网后会给电力系统带来巨大挑战[4-5]，因此如何最大限度消纳这些间歇性的可再生能源，已经成为新能源领域的热点问题[6-7]

文献[8]根据不同天气类型建立人工神经网络进行预测，在相对平稳的天气类型下预测效果良好，但在突变天气的预测效果较差；文献[9]提出了基于主因子分析的BP神经网络的光伏发电短期预测模型，但其未考虑季节影响，泛化能力不强，复杂天气下精度不高；文献[10]利用相似日聚类划分多个数据集，针对不同类型数据集分别建立基于长短期神经网络的光伏短期发电预测模型，提高了预测精度，但在相似日划分时未能充分考虑环境与天气的影响，预测精度有待提升；文献[11]针对BP 神经网络参数难以确定的问题，使用烟花算法优化参数，提升了预测精度，但神经网络在大样本下才能发挥更佳效果；文献[12]利用加权灰色关联投影法优化了相似日选取，但每次模型训练样本容量过少，在极端天气情况模型的泛化效果不佳；文献[13]运用经验模态分解EMD（empirical mode decomposition）建立模型，获得了较高的预测精度，但其分解存在明显模态混叠的现象，在一定程度上会影响模型的预测性能；文献[14]利用变分模态分解VMD（variational mode decomposition）平稳化处理光伏功率序列，对子序列预测重构后得出最终预测结果，一定程度上消除了模态分解导致的模态混叠的现象，但其对其对极端天气的处理能力不强，算法所需时间过长。

综上所述，针对现阶段光伏发电功率短期预测方法中的不足，本文提出基于改进K-means++自适应聚类和改进黑猩猩优化算法CHOA（chimpanzee optimization algorithm）优化最小二乘支持向量机LSSVM（least squares support vector machine）的短期光伏发电功率预测模型。首先，考虑不同季节下气象因素与光伏发电功率的影响程度不同，增强气象因素与发电功率之间的关联程度，对不同季节下气象因素进行自适应聚类，选用相似样本作为训练集。为了更好地利用天气因素，用相关性分析确定了与光伏发电功率相关的变量步长，同时考虑到数据的维度冗余度，用随机森林进行特征提取构建模型的输入特征集。

由于每类样本数量较少，易出现欠拟合的消极现象，因此使用在小样本情况下有较强拟合能力特性的最小二乘支持向量机可以有效改善模型的拟合能力[14]，再利用改进黑猩猩算法优化LSSVM模型的惩罚参数和核函数，增强模型对训练样本的拟合能力和对测试样本的预测能力。将所提模型分别与BP 神经网络BPNN（back propagation neural network）、长短期记忆LSTM（long short term memory）神经网络进行对比，并通过实验验证本文模型在精度和适用性方面的优势。

1 算法构建

1.1 最小二乘支持向量机

对于数据集X={(xi,yi)|i=1,2,…,n}，xi为第i个输入向量，yi为第i个输出向量，n为训练样本组数，则线性回归函数h(x)为

式中：α为线性权重系数矩阵；λ(xi)为非线性函数；β为偏置矩阵。

LSSVM优化目标函数为

式中：c为误差惩罚因子；ωi为经验误差。

约束条件为

拉格朗日函数为

式中：δ为拉格朗日乘子，δ=[δ1,δ2,…,δn]T；ω=[ω1,ω2,…,ωn]T。

根据Karush-Kuhn-Tucker条件，分别对α、β、ωi、δi求偏导，并令其等于0，则消去α、ωi可得到线性方程组为

式中：I=[1,1,…,1]T；h=[h1,h2,…,hn]T；E为n维的单位矩阵；Φ为核函数，Φ=λ(xi)Tλ(xi)，i=1,2,…,n。

LSSVM预测函数为

式中：K(xi,xj)为RBF核函数，其中i,j=1,2,…,n；σ为RBF函数的宽度。

1.2 黑猩猩优化算法

LSSVM 的核函数是提高泛化能力和学习精度的关键，而核函数易受条件限制，对惩罚参数敏感，易陷入过拟合。所以引入CHOA[16]对核参数进行寻优，获取模型的最佳支撑参数，进一步提升LSSVM的泛化能力。

1.2.1 黑猩猩优化算法（CHOA 算法）

黑猩猩优化算法是根据黑猩猩表现的不同智力与能力提出的一种启发式优化算法，其引用了概率和混沌因子，能较其他算法有更快的收敛速度和精度。

在自然界中，黑猩猩被分为5种不同等级：“驱赶者（Driver）”、“阻拦者（Barrier）”、“追捕者（Chaser）”、“攻击者（Attacker）”和“执行者（Executor）”，其中Attacker 黑猩猩权利最大，指挥整个种群的捕猎行动；Barrier黑猩猩是Attacker黑猩猩助手的角色，协助Attacker 黑猩猩指挥行动；Chaser 黑猩猩服从Attacker 黑猩猩和Barrier 黑猩猩的命令，同时支配下一阶层的Driver 黑猩猩；Executor 黑猩猩为最底层的黑猩猩，由余下的黑猩猩组成，是命令的执行者。

在黑猩猩种群中，黑猩猩在狩猎时会出现混乱捕猎行为，所以在优化中以50%的概率选择正常更新或混沌模型更新。黑猩猩包围猎物的数学模型为

式中：t为当前迭代次数；Xprey(t) 为当前猎物的位置；dg为黑猩猩与猎物之间的距离；mg为混沌映射矢量；Ag、Cg为系数向量，其更新表达式为

式中：rand()为[0,1]区间的随机向量；ag(t) 为收敛因子，随着t增加逐渐较小，其更新表达式为

式中，Tmax为最大迭代次数。

为便于理论研究和公式化处理，定义种群中最优个体为Attacker黑猩猩，次优个体为Barrier黑猩猩，第3优个体为Chaser黑猩猩，第4优个体为Driver黑猩猩，其余为Executor黑猩猩。

Executor黑猩猩位置由Attacker、Barrier、Chaser、Driver共同决定，其更新公式为

式中：Xu为Executor 黑猩猩中第u只黑猩猩的位置；Di(i=1,2,3,4)为第u只Executor 黑猩猩与4 个最优个体黑猩猩之间的距离；XAttacker、XBtarrier、XChaser、XDriver分别为4个最优个体黑猩猩的当前迭代位置；X1、X2、X3、X4分别为4个最优个体黑猩猩的更新位置；Ag1～Ag4、Cg1～Cg4、mg1～mg4分别为Ag、Cg、m中的4个系数向量。

1.2.2 改进的黑猩猩算法（PCHOA 算法）

虽然CHOA算法引入混乱捕猎行为加快了收敛速度，但还存在精度低和收敛慢等不足。为了进一步提高算法搜索能力和收敛性能，引入粒子群算法记录黑猩猩个体经历的最佳位置以及群体最佳位置，来更新当前Executor黑猩猩的位置，表达式为

式中：c1、c2为学习因子；r1、r2为[0,1]区间的随机向量；Xbest为黑猩猩最优的位置；P1、P2、P3、P4为惯性权重系数，其具体公式为

其PCHOA算法流程如图1所示。

图1 改进黑猩猩优化算法流程Fig.1 Flow chart of improved chimpanzee optimization algorithm

步骤1设置相关参数，本文种群数N为30，最大迭代次数为80。

步骤2初始化黑猩猩种群位置。

步骤3计算适应度，确定前4个最优解XAttacker、XBtarrier、XChaser和XDriver。

步骤4更新Ag、Cg，按照式（14）更新执行黑猩猩的位置。

步骤5通过粒子群算法的群个体记忆机制，按照式（15）更新执行黑猩猩位置。

步骤6判断是否满足迭代次数，若满足输出最优黑猩猩位置XAttacker，否则继续迭代。

步骤7获得最佳参数，保存最优LSSVM模型。

1.3 改进的K-means++聚类算法（DK 算法）

传统的K-means++聚类算法原理简单，适用性强，在光伏功率初始数据处理上得到广泛的适用[17]，但是算法需要人为定义K值，随机选取聚类中心，会受数据分布、人为因素的影响，处理精度不高。本文采用密度聚类算法[17]的思想，综合考虑季节内、季节间的差异度，根据综合评价函数自适应得出最佳K个聚类中心，降低算法陷入局部最优的可能。

样本xi、xj之间的距离为

式中，M为聚类样本维度。

距离阈值内的局部密度ρi为

式中：Dt为阈值距离；z为聚类样本数目。

密度聚类初始聚类中心mk的更新公式为

式中：k为聚类数目；X为总数据集。

综合评价函数为

式中：Dout为不同类样本之间的欧式距离；Din为同类样本之间的距离。

F(k)越接近1，聚类效果越好；F(k)越接近-1，聚类效果越差。

改进算法的步骤如下。

步骤1输入数据X，阈值距离Dt，计算xi、xj之间的距离d(xi,xj)，计算距离阈值Dt内的局部密度ρi。

步骤2对ρi排序，选择max{ρi} 为第1个聚类中心m1，根据max{d(x，m1)}选出离m1最远且密度最大的聚类中心m2，依次按照式（19）获得其最佳聚类中心mi。

步骤3迭代计算，根据式（20）得出最优的F(k)，对应的k即为最佳聚类数目K。

步骤4计算样本xi到mi的距离d，划分样本xi到最近的mi。

步骤5重新计算各簇类的平均值，判断聚类中心是否改变。未改变则直接输出聚类结果，若改变返回步骤4重新迭代。

步骤6保存聚类结果，等待预测模型调用。

2 预测模型的建立

2.1 输入量选择

不同季节下气象因子有很大不同，光伏功率的输出变化也会深受影响。考虑不同季节对光伏输出功率的影响，随机选取5 d 进行斯皮尔曼相关性分析，结果如表1所示。

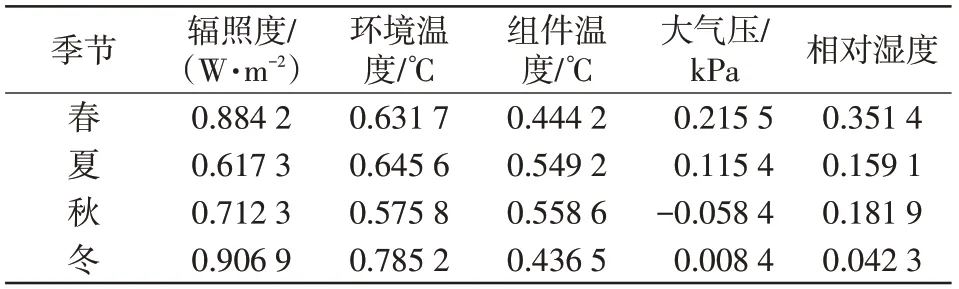
表1 斯皮尔曼相关性分析Tab.1 Spearman correlation analysis

由表1 可知，春季辐照度和环境温度对光伏出力呈现强相关，组件温度、大气压、湿度呈现弱相关；在夏、秋、冬3季，辐照度、环境温度、组件温度与光伏出力呈现强相关，而大气压与湿度几乎对光伏出力没有影响。因此，春季将5个气候因素都作为输入特征；而在夏、秋、冬3 季仅选取辐照度、环境温度、组件温度3个环境因素表征光伏出力特征。

考虑t+1时刻的光伏功率与前n个时刻功光伏率有很强的相关性，光伏输出功率自相关性分析，如表2所示。

表2 输出功率的自相关性Tab.2 Autocorrelation of output power

由表2可知，随着时间的推移，光伏出力与前n个时刻的相关性逐渐减弱，因此选用前5个时刻功率已经能基本表征t+1时刻的功率。

2.2 基于随机森林的输入特征构建

综上所述，构建的输入/输出变量如表3所示。

表3 预测模型的输入/输出变量Tab.3 Input/output variables in prediction model

2.3 预测模型指标

采用平均绝对误差(MAE)、均方根误差(RMSE)、拟合优度(R2)衡量预测模型性能，它们分别定义为

式中：为预测值；Pi为实际值；为平均值；N为预测点个数。

2.4 基于PCHOA-LSSVM 的功率预测模型

基于上述讨论，本文构建DK-PCHOA-LSSVM的光伏输出功率预测模型，其流程如图2所示。

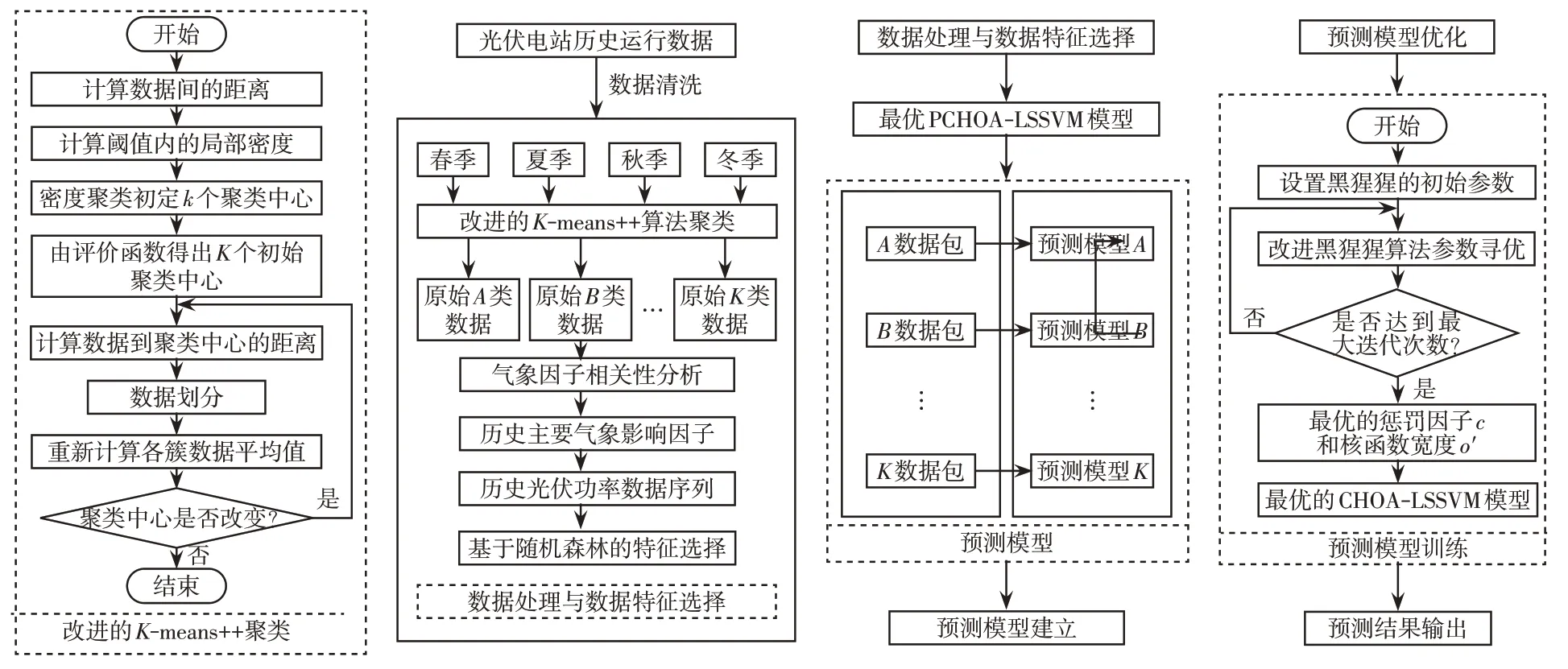
图2 预测模型流程Fig.2 Flow chart of predictive model

步骤1数据清洗，以天为单位剔除由于异常、故障等原因产生的不良数据。

步骤2利用改进的K-means++算法将季节数据聚类，将数据分类为A～K类相似日数据。

步骤3对步骤2中分类得到的相似日数据进行相关性分析，选择主要的气象因子和历史光伏输出功率数据作为输入特征，再利用随机森林算法消除数据的冗余性。

步骤4对步骤3 数据归一化，转化为A～K类相似日数据包。

步骤5初始化黑猩猩优化模型参数，将样本的训练集输入到改进的CHOA-LSSVM 模型中进行训练，直到获得最优的训练模型。

步骤6保存最优训练模型，输入预测样本进行测试。输出模型评估指标MAE、R2、RMSE结束模型。

3 算例实验分析

3.1 数据描述

本算例实验数据来源于我国宁夏回族自治区某100 kW 光伏电站监数据，样本数据为2020 年1 月1 日—2020 年12 月31 日的实测光伏功率和环境监测仪所测得到的太阳辐照度、组件温度、空气温度、相对湿度、大气压力的数据集，其采样时间为15 min/次，其中各监测设备运行情况正常，数据可靠。由于晚间时段光伏出力为0，所以截取每日05：00—19：00 的数据频段作为输入样本，共计365天的数据（21 900 个样本点）。考虑不同季节对光伏输出功率的影响，按照季节将全年数据分为4个季节子集，其中12 月—次年2 月为冬季，3—5 月为春季，6—8 月为夏季，9—11 月为秋季。将各季节实际运行数据划分为2个部分，同类型历史气象及光伏发电功率数据作为训练集，待测日温度和风速为数值天气预报NWP（numerical weather prediction）数据及光伏发电功率数据作为测试集，对待预测日05：00—19：00时段进行提前24 h预测。

3.2 聚类结果分析

利用改进的K-means++自适应聚类，不同季节天气类型聚类天数如表4所示。

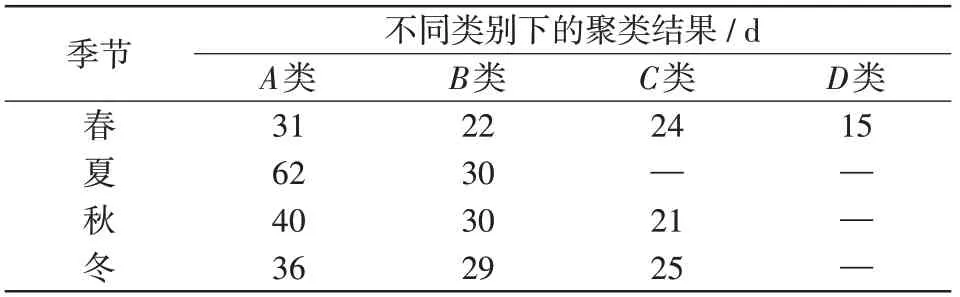
表4 不同季节聚类天数Tab.4 Clustered days by season

由表4可知，数据的聚类簇数与季节有关，如春季有A类31 d，B、C、D类分别为22 d、24 d、15 d，而夏季只被分A类和B类，其中，A类为传统意义下的晴空类数据，B、C、D类为非晴空类，包括多云、雨天（大雨，小雨，暴雨）、阴天、雪天等各种天气类型。

虽然不同年份、不同季节气象数据存在差异性、随机性，但改进的K-means++聚类能自适应出最优聚类数目，能以此建立不同数量的预测模型，能更好地适应气候、季节变化，应对极端天气的出现，提高了模型的抗干扰能力和稳定性。

3.3 预测结果分析

根据不同季节的聚类结果，分别采用PCHOA和CHOA算法对LSSVM模型进行寻优，得到各类型下最优核参数向量，从而获得最优LSSVM 预测模型。为验证改进K-means++聚类算法和PCHOA 优化LSSVM 模型的优良泛化性能，从数据中随机抽取2020 年2 月22 日、5 月27 日、8 月24 日、11 月14日数据进行预测，将本文改进K-means++聚类的改进黑猩猩优化支持向量机模型（DK-PCHOA-LSSVM）与普通K-means++聚类的改进黑猩猩优化支持向量机模型（K-PCHOA-LSSVM）、改进K-means++聚类的普通黑猩猩优化支持向量机模型（DKCHOA-LSSVM）的预测结果进行比较。预测曲线分别如图3～图6所示。

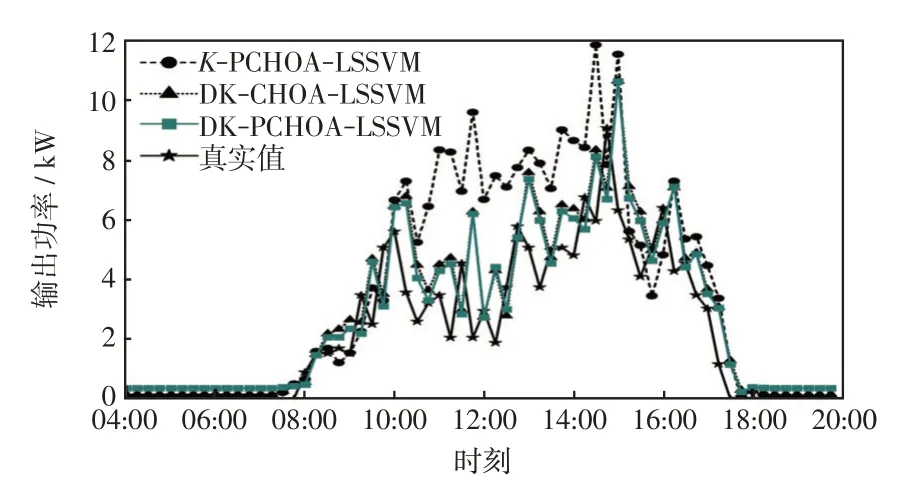
图3 2 月22 日各模型对比Fig.3 Comparison among models on February 22

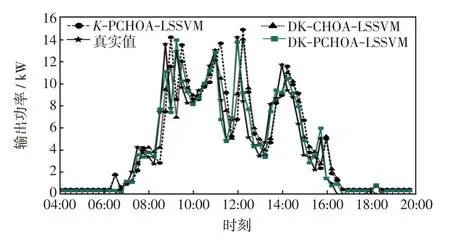
图4 5 月27 日各模型对比Fig.4 Comparison among models on May 27

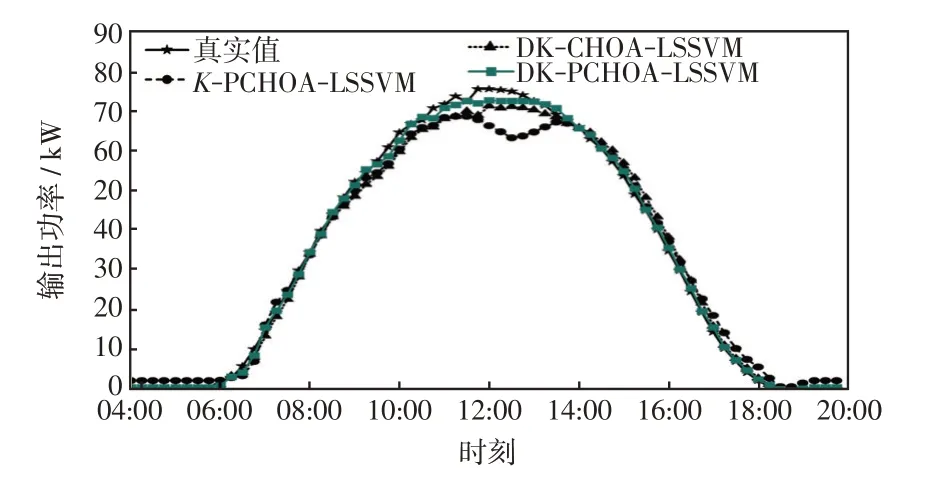
图5 8 月24 日各模型对比Fig.5 Comparison among models on August 24

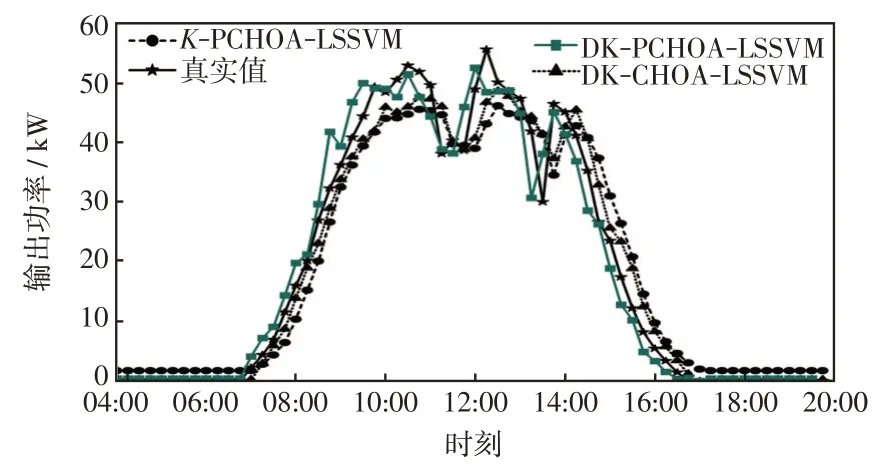
图6 11 月14 日各模型对比Fig.6 Comparison among models on November 14

从图3～图6 可知，8 月24 日的晴空条件下KPCHOA-LSSVM、DK-CHOA-LSSVM、DK-PCHOALSSVM 3 个预测模型均能良好预测光伏发电功率的变化，但K-PCHOA-LSSVM有更大的误差；在2月22 日的非晴空条件下，K-PCHOA-LSSVM 模型的跟踪性能最差，特别是在10：00—15：00 这段时间，预测值偏离实际值较多，而其他两类模型偏离程度较小，这表明基于自适应类别划分相似日的数据处理是改善B、C、D类非晴空模型预测性能的有效途径；而在5月27日和11月14日，DK-PCHOA-LSSVM预测模型很好地跟随了实际输出功率，偏离程度最小。而K-PCHOA-LSSVM 和DK-CHOA-LSSVM 预测结果相近，在功率波动时刻偏离误差较大，表明改进黑猩猩算法提高了算法搜索能力，增强了模型泛化能力和挖掘数据随机波动规律的能力，提升了B、C、D类非晴空模型预测精度。

分别计算各模型输出功率的MAE、R2、RMSE，结果如表5 所示。从表5 可知，对比于目前流行的传统K-means 相似日选取方法，改进的K-means++在B、C、D 类非晴空天气下R2提高了21%左右，RMSE减小40%左右，MAE减了37%左右；在A类晴空天气下各预测指标也均有提升。从表5 中也能看出，PCHOA-LSSVM算法与CHOA-LSSVM算法相比，有着更优的拟合优度，更小的误差。

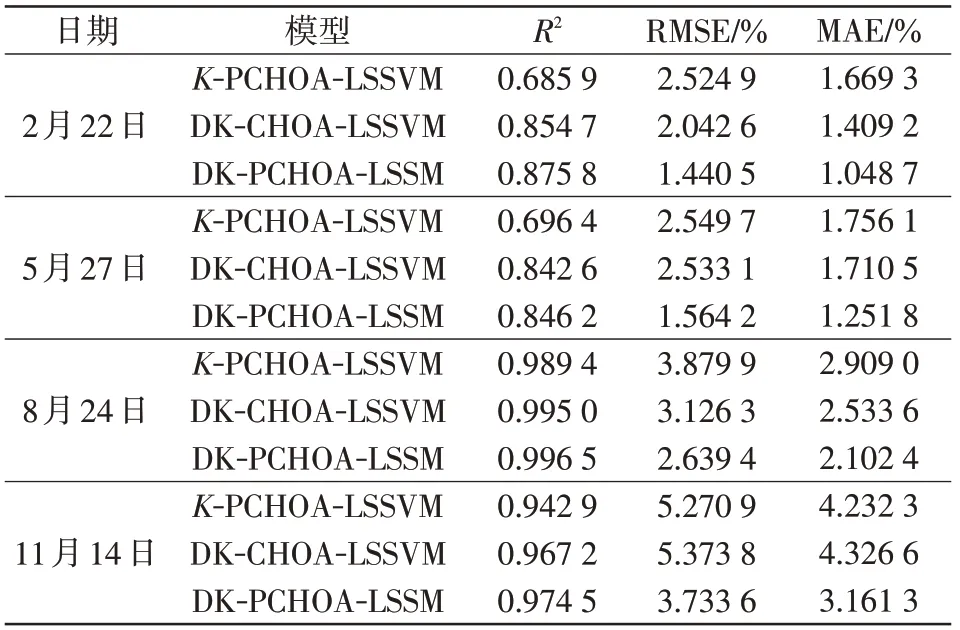
表5 模型评价指标Tab.5 Model evaluation indicators

为验证PCHOA-LSSVM 的预测能力，在改进的K-means++聚类下将本文预测模型与文献天牛须搜索算法优化的BP 神经网络（DK-BAS-BPNN）和长短期神经网络（DK-LSTM）预测模型进行对比，4 天的对比效果分别如图7～图10 所示。由图7～图10可知，在晴空天气下DK-PCHOA-LSSVM 较参考模型有更高的精度；在非晴空天气下，DK-BAS-BPNN和DK-LSTM 模型的预测值与实际偏差较大，尤其是对突变点的追踪能力不强，而DK-PCHOA-LSSVM 模型的偏差程度最小，能对光伏出力的突变作出很好的预测，体现了较好预测性能，表现出PCHOA-LSSVM在小样本数据集和数据集波动较大时较强的拟合能力，有效避免了神经网络等方法中常出现的局部最优合和过拟合等问题。

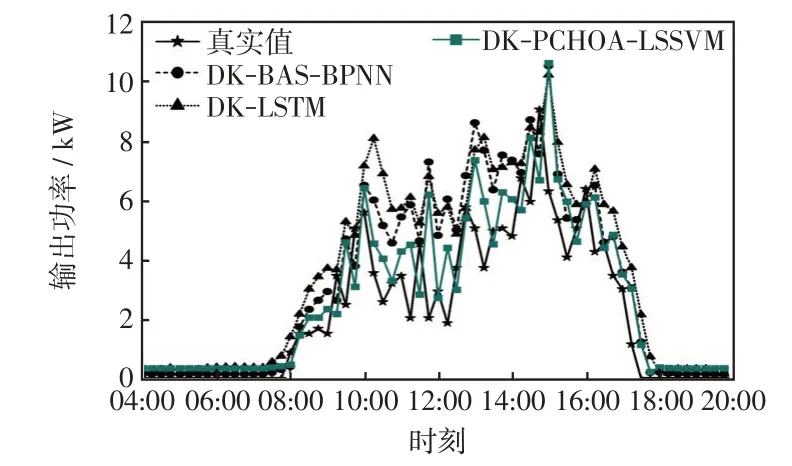
图7 2 月22 日各模型对比Fig.7 Comparison among models on February 22

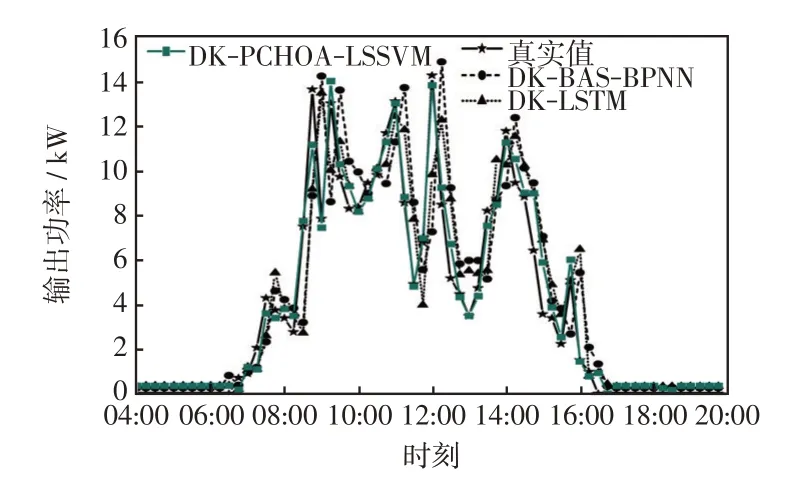
图8 5 月27 日各模型对比Fig.8 Comparison among models on May 27

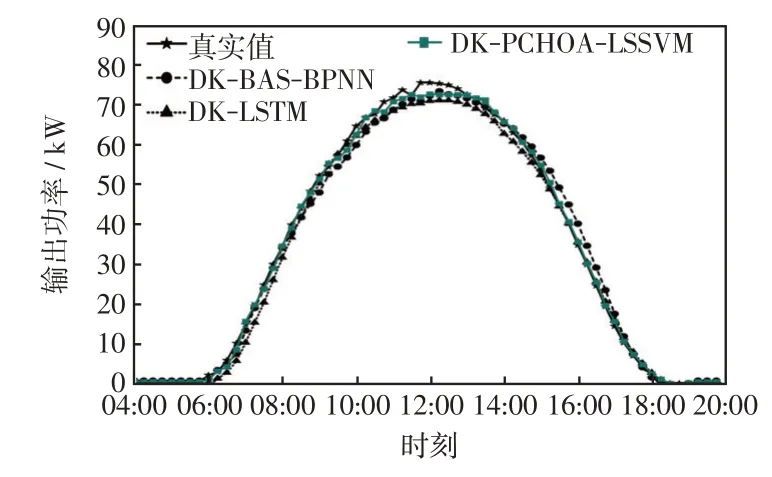
图9 8 月24 日各模型对比Fig.9 Comparison among models on August 24

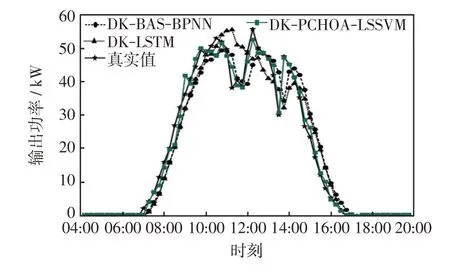
图10 11 月14 日各模型对比Fig.10 Comparison among models on November 14

为进一步验证本文方法的泛化能力和普适性，随机抽取光伏电站功率变化波动大的5 d，即11 月24 日—11 月28 日进行连续5 d 功率滚动预测。其预测结果如图11所示，预测误差如表6所示。

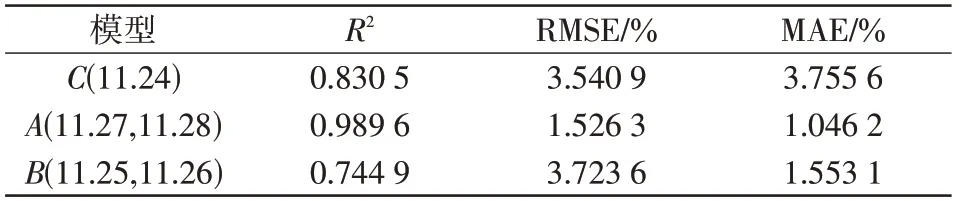
表6 模型评价指标Tab.6 Model evaluation indicators

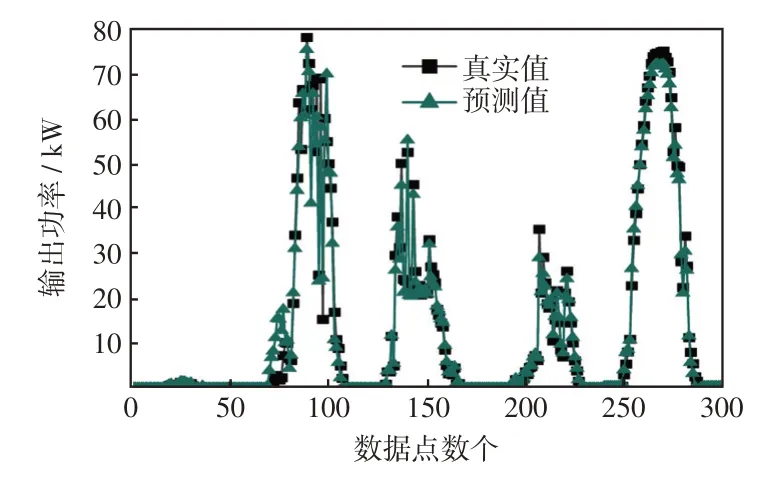
图11 连续5 d 预测结果对比Fig.11 Comparison of prediction results for five consecutive days

由表6 可知，预测误差的MAE、RMSE 均小于5%。基于以上对比分析，本文预测模型相较于传统方法在天气大波动下也能良好地追踪实际输出功率，适用于晴空、非晴空条件下的光伏发电短期功率预测。

4 结 论

（1）基于传统K-means++的不足，引入密度聚类和综合评价函数评估聚类结果，获得自适应的Kmeans++算法。聚类数目随着季节气候变化而发生改变，克服了人为设置聚类数和随机选取聚类中心的缺点，充分考虑了光伏发电功率预测中各气象相关因素的影响，为提取待预测光伏功率的特征提供依据。

（2）基于黑猩猩算法收敛速度过慢、易陷入过拟合的缺点，引入粒子群算法记录黑猩猩个体经历的最佳位置以及群体最佳位置来优化黑猩猩算法，通过与原始方法比较，改进的黑猩猩算法能提高算法搜索能力，优化效果明显。

（3）构建的DK-PCHOA-LSSVM 的功率预测模型不仅融合多源外部气象因素模块，克服了收敛速度慢等弊端，而且PCHOA 算法实时优化LSSVM 的核函数和惩罚因子，提高了模型预测的适应度，预测精度较其他传统模型在天气大波动下也能良好追踪，实际输出功率有显著提升，能够满足短期实时调度需求。