aLMGAN-信用卡欺诈检测方法

李占利，唐 成，靳红梅

(西安科技大学 计算机科学与技术学院，陕西 西安 710054)

0 引 言

近年来，随着机器学习和深度学习的迅速发展，研究人员已经提出了许多不同层次的信用卡欺诈检测方法。Suraj Patil等[7]使用决策树分类的方法来检测信用卡交易的异常行为，在精确性和稳定性方面有很好的表现，但该技术需要确定标签数据，缺乏泛化性；Bertrand Lebichot等[8]提出了一种基于图的半监督信用卡欺诈检测系统，使用一种集体推理算法来检测欺诈行为，但这种方法未考虑信用卡数据中出现的类不平衡问题，很难判断具体的检测效果；Mary Frances Zeager等[9]引入合成少数过采样技术(SMOTE)来缓解类失衡，但这种方法所生成的点很可能在多数类区域内，这会使得分类变得困难；Dawei.Cheng等[10]将注意力三维卷积神经网络用于信用卡欺诈检测，提出了一种基于时空注意力机制的三维卷积神经网络方法，拥有一定的实时性，但容易出现漏检现象；Altyeb Altaher Taha等[11]利用优化的光梯度增强机(OLightGBM)检测信用卡交易中的欺诈行为，但该方法未考虑信用卡数据集的不平衡性，查全率较低；Ibtissam Benchaji等[12]使用SMOTE处理类不平衡问题，将注意力机制运用于LSTM深度递归神经网络，但该方法对SMOTE生成数据具有很好的检测效果，但是对真实交易数据检测效果不佳。

针对以上问题，本文首先采用SMOTETomek进行数据清洗，并基于PCA和t_SNE设计混合数据降维方法对数据进行降维处理，从而减轻模型负担，提升模型效果；其次提出一种基于闵可夫斯基距离损失函数的生成对抗网络对预处理后的数据进行学习建模，以此检测信用卡交易中的欺诈行为。综上所述，本文贡献主要有以下3个方面：

(1)将PCA和t_SNE降维算法相融合，提出P_SNE算法，在具有良好数据降维效果的同时可以处理数据重叠问题。

(2)提出了一种基于LSTM和aMLP的生成对抗网络用于处理信用卡欺诈检测问题，具有更好的检测性能。

(3)提出一种基于闵可夫斯基距离的生成对抗网络损失函数(Min-loss)，用于解决生成对抗网络模型训练不稳定和模式崩溃问题，对于最终模型检测效果的提升具有很大的帮助。

1 本文方法

为了解决信用卡欺诈检测中的数据不平衡重叠和维度诅咒问题，本文首先提出一种基于PCA和t_SNE的混合数据降维方法，对数据进行预处理操作；其次提出一种基于LSTM和aMLP的端到端一类生成对抗网络算法，对预处理后的数据进行训练检测。本章将详细描述该模型的基本思想及其实现过程。

1.1 基于PCA和t_SNE的混合数据降维方法(P_SNE)

信用卡数据集中往往存在着大量的数据重叠和维度诅咒问题，这会影响模型的判断。在本节中，使用SMOTETomek技术对数据进行清洗，清除数据中的重叠以及异常数据部分，从而获得纯净的正常训练数据，这对于之后的生成对抗网络模型是至关重要的。

然而，经过清洗后的数据其维度不会发生改变，会使得模型陷入“维数诅咒”，从而导致模型训练难度增大，最终影响模型的检测效果。因此，本节中融合PCA和t_SNE降维技术对原始特征计算一个新的特征空间。通过PCA方法对原始数据进行简单降维，缩小数据维度，但如果只用PCA降维，会使得数据产生大量的类重叠，从而影响模型的学习判断，使得最终分类效果不佳；因此，本文在PCA降维之后加入t_SNE降维，对PCA降维后的数据重新进行特征映射，以此避免产生类重叠问题导致模型效果不佳，通过t_SNE再降维后，新的特征在原始数据方差最大的方向上，然后利用这些新的特征构造一个更加低维的特征空间，在这个新的特征空间中，信用卡数据特征以其特征权值表示，这将使得模型训练更加清晰化，有效地避免了边缘模糊问题。算法详细过程如下：

P_SNE：基于PCA和t_SNE混合数据降维方法

输入：样本集D={x1，x2，…，xn}；低维空间维数k

过程：

(2)计算样本的协方差矩阵XXT；

(3)对协方差矩阵XXT做特征值分解；

(4)取最大的m个特征值所对应的投影矩阵W=(ω1，ω2，…，ωm)；

(5)将投影矩阵对应作为中间数据 {x(1)，x(2)，…，x(m)}；

(6)初始化困惑度参数用于求解σ，迭代次数T，学习率η和动量α(t)；

(7)开始优化：

计算高维空间中的条件概率pi|j

使用正态分布N(0，10-4) 随机初始化Ym*k矩阵，其中k表示最终降维维度；

从t=1，2，…，T进行迭代：

计算低维空间中的条件概率

其中y(i)为降维后数据；

计算损失函数C(y(i)) 对y(i)的梯度

更新随机矩阵Y

输出：Y

通过P_SNE数据降维，消除了重叠数据和“维数诅咒”对模型训练的影响，为进一步的数据处理减少了存储和计算的复杂性。

1.2 基于LSTM和aMLP的生成对抗网络(aLMGAN)

信用卡欺诈检测数据中往往存在着极度的类不平衡，这样对模型的训练带来了很大的困难，使得模型会严重偏向于多数类，从而很难检测出信用卡交易中的欺诈交易。本文提出一种基于生成对抗网络的端到端一类分类算法(aLMGAN)，aLMGAN只使用正常多数类数据来训练，网络在对抗学习中生成器不断生成近似于真实的数据以欺骗判别器，而判别器对原始数据和生成数据不断进行辨别，生成器和判别器在欺骗和辨别中不断学习训练，最终判别器形成极度靠近真实数据的特征模式，对于远离正常数据特征的异常数据具有很好的排外作用，以此达到良好的信用卡欺诈检测效果。本文提出的生成对抗网络模型结构如图1所示。

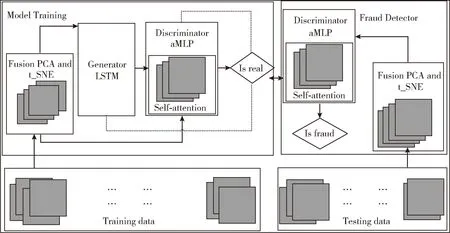
图1 aLMGAN模型结构

从上边结构图中可知，该算法主要由训练和测试两部分组成。左侧为生成对抗网络框架，首先将正常交易数据送入P_SNE数据降维，然后将降维后的数据送入生成对抗网络，通过迭代训练得到生成器和判别器模型通过生成器的输出更新生成器和判别器参数，使得生成器所生成数据更加接近于真实数据，从而欺骗判别器；而判别器能够以高灵敏度区分生成数据和真实数据。右侧为异常检测过程，应用生成对抗网络训练的判别器来计算正常数据和异常数据的异常评分。

1.2.1 生成器

LSTM对时间序列数据的特征提取具有良好的表现，因此，在本文中，采用LSTM作为生成器网络，对信用卡正常交易数据进行特征提取和重建，学习正常交易数据的分布，更好地重建近似于真实数据的生成数据，以欺骗训练判别器网络模型，最终提升信用卡欺诈检测效果。为了实现这一目标，提出两个损失函数

(1)

(2)

以上两个公式中，R表示生成器，即LSTM，C表示判别器，即aMLP，X表示训练数据；式(1)表示重建损失，本文设置为L2损失函数；式(2)为生成对抗网络损失函数的一部分，本文采用L1损失函数，通过这两个损失函数来引导生成器产生与输入数据具有相同分布的输出，并混淆和训练判别器模型，则生成器的总体培训目标为

(3)

式中：pt表示真实交易的分布模式。

1.2.2 判别器

在本文中，设计一种基于自注意力机制的多层感知机判别器模型(aMLP)，旨在将原始数据与LSTM重建数据分离。因为信用卡欺诈检测数据往往具有大量的数据重叠问题，这对于很多弱分类器而言很难达到预期的检测效果，所以选择MLP强分类器作判别器模型，并在判别器模型中加入self-attention，使得判别器对欺诈交易具有更高的敏感度。该模型的最终输出是一个表示概率的单一值，其判别器损失可以表示如下

(4)

式中：pZ表示从随机空间中抽取的一组子序列，λ是一个随机参数在本文中设置为1.85，C表示判别器，R表示生成器，X为训练数据。

在判别器中self-attention模块的基本思想就是想让模型学会注意力，即能够忽略无关信息而关注重点信息，通常情况是利用相关特征学习权重分布，再用学习出来的权重加在特征之上进一步提取相关知识，加权可以作用在原数据上，也可以作用在空间尺度、通道尺度上，如图2所示是self-attention模块的基本结构。

图2 自注意力模块结构

其中自注意力机制基本原理是self-attention模块通过1*1卷积分为f、g和h，首先将f和g进行相似度计算得到权重，常用的相似度函数有点积、拼接、感知机等。其次使用一个softmax函数对这些权重进行归一化处理，最后将权重γ和相应的h进行加权求和得到最后的attention值[20]。

在本文中，γ初始化为0，首先依赖局部原本的x，然后逐渐增加非局部权重，最后将self-attention模块与MLP模型融合作为判别器模型，将经过训练的判别器模型作为信用卡欺诈交易检测模型，对新产生数据实现欺诈检测。

1.2.3 基于闵可夫斯基距离的损失函数(Min-loss)

在生成对抗网络中，损失函数不仅用于衡量网络训练效果，而且对于指导生成器和判别器的训练起着决定性的因素。传统生成对抗网络的交叉熵损失，比较擅长于学习类间的信息，但是只关心对于正确标签预测概率的准确性而忽略了其它非正确标签的意义，从而导致模型学习到的特征比较松散，最终产生模式崩溃。为避免这一问题的发生，方便更好地优化生成对抗网络的训练，本文通过对比L1、L2、交叉熵损失函数、最小二乘损失函数的效果，通过研究闵可夫斯基距离公式，对这一类距离中的曼哈顿距离、欧氏距离和切比雪夫距离进行加权融合，设计出新的生成对抗网络损失函数，在这种损失函数下，最终生成器和判别器的极大极小博弈可表示为

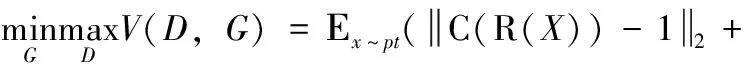
(5)

式中：λ是一个随机参数，在本文中设置为1.85，用于平衡不同距离函数对整体损失函数值的占比，防止由于预测值与真实值差异过大或过小而造成的梯度爆炸问题，从而提升模型稳定性，最终达到更高精度。

2 实 验

2.1 实验环境与数据集

2.1.1 实验环境

本文采用的硬件环境为GeForce RTX2060显卡、Intel(R) Core(TM) i7-10875H CPU，16 G内存；软件平台为windows10操作系统，python3.6.13版本；Tensorflow2.6.2-GPU版本；CUDA11.2版本；cuDNN8.1版本。

2.1.2 实验数据集

data1数据集(data1数据集网址https：//www.kaggle.com/datasets/mlg-ulb/creditcardfraud)包含284 807笔信用卡交易，这些交易于2013年9月在欧洲为期两天的时间内收集，其中只有492起欺诈案件占总交易数据的0.172%，其它234 315起案件为正常交易，表明数据集高度不平衡。每笔交易有30个特征，其中28个是由主成分分析获得，另外两个是时间和金额，这28项特征被列为V1至V28，但由于保密问题，未提供进一步信息。时间特征表示当前事务和第一个事务之间经过的时间，金额特征是交易中的金额，由于该数据已被标准化，在训练过程之前无须再进行数据处理。对于训练集和测试集的划分，本文从492个欺诈案例中选择490个案例，并从234 315个正常案例中选取相同个数的案例以生成一个平衡良好的测试集，剩余的233 825个正常案例构成实验训练数据集。data1数据集部分数据样例如图3所示。

图3 data1数据样例

data2数据集(data2数据集网址https：//www.kaggle.com/datasets/kartik2112/fraud-detection)是一个模拟信用卡交易数据集，包含2019年1月1日至2020年12月31日期间的合法和欺诈交易。它涵盖了1000名客户的信用卡，这些客户与800家商家进行交易，其中包含1 842 743笔正常交易和9651笔欺诈交易，同样是一个高度不平衡数据集。每笔交易有21个特征，与data1不同的是data2未进行加密处理，数据中存在数值类型字段和字符类型字段，本文采用自编码器对原始数据进行特征编码，并从1 842 743个正常案例中采用随机下采样方法选取9651个与所有欺诈案例构成平衡测试集，剩余正常案例全部作为实验训练数据集。data2数据集部分数据样例如图4所示。

图4 data2数据样例

本文在以上两个kaggle基准信用卡欺诈检测数据集上训练测试异常检测模型的性能。在两个数据集中均采用随机下采样生成平衡良好的测试集，其余正常案例则构成实验训练集，所有对比实验都在这两个数据集上进行测试，而针对不同方法训练集做相应的正负样本占比调整。

2.1.3 模型参数设置

在本文中，所有实验均在以上两个数据集中进行，对于本文所提出的方法使用深度为3和隐藏层神经元个数为100的LSTM网络作为生成器，使用深度为4和隐藏层神经元个数为100的MLP网络作为判别器模型。在训练中，本文批量大小设置为300，训练轮数设置为100，潜在空间的维数设置为15；值的注意的是，本文使用Adam[23]算法来优化网络训练，并使用双尺度更新原则，生成器和判别器学习率分别设置为5e-3和1e-3。

在本文所提出方法中，超参数对最终检测效果的影响主要来自于PCA降维维度m、t_SNE降维维度k和损失函数中的λ值。不同的降维维度对最终实验效果的影响较大，这需要根据原始数据维度以及数据特征进行维度选择；而损失函数中的λ值对于模型稳定性的训练起着关键性作用，这直接决定了模型训练的最终结果。经过分析总结，本文最终设置PCA降维维度m为10，t_SNE降维维度k为3，损失函数中λ值为1.85。

2.2 实验结果

本文使用STMTETomek进行数据清洗，并通过混合降维方式P_SNE对原数据进行降维操作，以此来解决数据重叠问题对最终检测效果的影响。因此在本实验中，首先使用2.1.2节所提到的data1数据集进行消融实验，通过实验对比来验证所提方法对总体信用卡欺诈检测准确性、精确度、召回率和F1分评价指标的提升，其消融实验结果见表1。

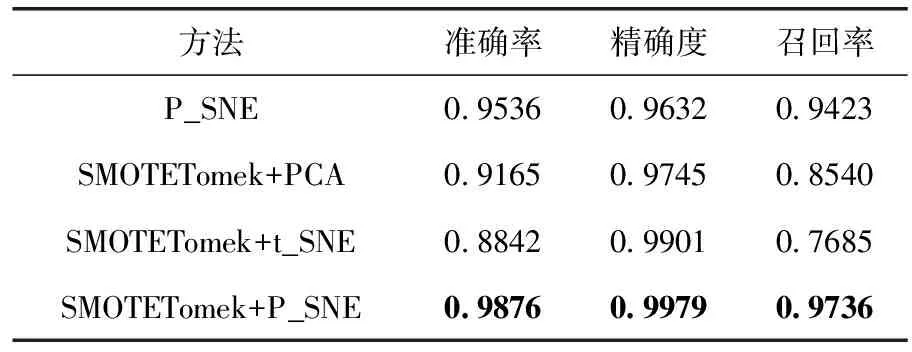
表1 数据去重对最终效果影响消融实验对比

由表1可以看出，本文所提出的混合降维方法P_SNE相对于加入SMOTETomek的PCA和t_SNE都表现出了更高的准确性和召回率。而在P_SNE混合降维方法前加入SMOTETomek后，能够在准确性、精确度和召回率3个方面表现出比前者更好的效果，由此验证SMOTETomek数据清洗加上P_SNE是对数据重叠问题更有效的解决方法。

为了验证本文所提出的信用卡欺诈检测方法的有效性，实验首先对aLMGAN采用上述数据进行了测试，在评估中，将本文方法(aLMGAN)测试结果执行混淆矩阵的可视化，以更加清晰直观展示其最终效果。混淆矩阵结果如图5和图6所示。

图5 data1结果混淆矩阵

图6 data2结果混淆矩阵

从图5和图6中可以看到，本文所提方法在data1上检测到了所有全部的异常数据，只有8条正常数据被误判为了异常，基本可以实现完全检测。而对于data2在9650条异常数据中准确检测到了9290条，在9649条正常数据中只有854条被误报，能够检测到绝大多数的异常交易，并且误报率很小。以此验证本文所提出算法的良好性能，不但可以最小化被归类为欺诈的正常交易数量，也能够检测到罕见的欺诈性交易，这对于现实生活中的金融服务是至关重要的。

为了进一步评估aLMGAN的性能，本文将aLMGAN与以下算法进行对比实验(AE(Sakurada M，Yairi T 2014)[15]、LSTM-attention(Benchaji I，Douzi S，El Ouahidi B 2021)[12]、MLP(Tang，Deng，and Huang 2015)[20]、OCAN(Wu T，Wang Y 2021)[19]、DAMVI(Goyal A，Khiari J 2020)[21])，准确度(Auc)、精度(Pre)、召回率(Rec)和F1分数评价指标的实验结果见表2和表3。

表2 基于data1数据集的实验效果对比

表3 基于data2数据集的实验效果对比

如表2和表3所示，本文提出的方法在data1和data2中的准确度分别为0.9876和0.9371，F1分数分别为0.9856和0.9304，高于其它基线方法，这表明同时考虑精确度和召回率的情况下，本文所提出的模型达到了最佳的性能。值得注意的是，对于data1所有基线方法都拥有较好的效果，而对于data2只有DAMVI方法能够达到90%的准确性，而其它基线方法效果较差，这意味着这些基线方法只能针对特定的数据才能具有较好的效果，而随着不法分子欺诈技术的不断更新，很难起到一定的作用；相对于这些方法，本文方法具有很好的适用性，能够适应不同的信用卡交易数据，并实现良好的检测效果。

与此同时，为评估本文所提降维方法和损失函数的真实有效性，本文在上述两个数据集上进行了消融实验，采用与上述对比实验相同的评价指标进行对比，结果见表4和表5。

表4 基于data1数据集的消融实验结果对比

表5 基于data2数据集的消融实验结果对比

在表4和表5的消融实验中，同样使用了前文所提到的两个kaggle数据data1和data2。由表4和表5可知，本文所提数据降维方法和损失函数相比于PCA和t_SNE数据降维方法以及均方误差和交叉熵损失具有更好的表现，能够更加准确全面地检测到异常交易。

最后，本文绘制aLMGAN的接收机工作特性曲线(ROC)和准确召回率曲线(AUPRC)(如图7～图10所示)。由图7和图8不难看出，aLMGAN在高查全率的同时兼顾低误报率，防止因为误报而对他人造成不良影响；通过观察图9和图10可知，aLMGAN在两个数据集中ROC曲线下面积AUC的值分别为0.9878和0.9588，均接近于1，这表明aLMGAN在信用卡欺诈检测中具有良好的分类效果。

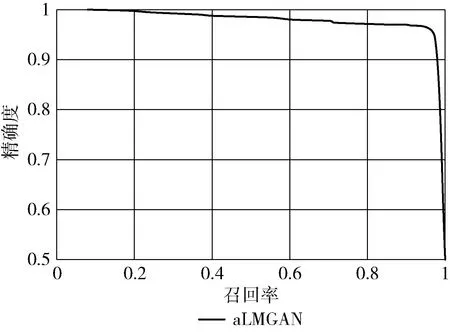
图7 基于data1数据集的AUPRC曲线

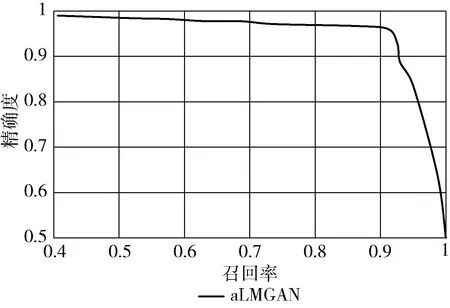
图8 基于data2数据集的AUPRC曲线

图9 基于data1数据集的ROC曲线

图10 基于data2数据集的ROC曲线

3 结束语

本文提出一种端到端一类分类生成对抗网络(aLMGAN)信用卡欺诈检测方法，并使用两个真实数据集进行实验，通过与AE、MLP、LSTM-attention、OCAN和DAMVI这5种信用卡欺诈检测算法进行性能比较，并结合实验结果可知，aLMGAN在两个信用卡交易数据集中均获得了最高的检测准确率和F1分数，由此可见该方法具有更好的类不平衡适应能力，表现出了更稳定、更准确的检测效果。与此同时，实验发现本文所提方法能够很好地适应于不同的数据集，之后可以将其引入其它应用领域。