基于多Agent 传动关系的股市趋势预测

鲍志，姚宏亮，方帅，杨静，俞奎

（合肥工业大学计算机与信息学院，安徽 合肥 230601）

0 引言

股票市场是一个非线性、不稳定的动态系统，导致股市趋势预测成为机器学习领域的一个研究难点。同时，股市波动具有内在规律，且产生了大量的数据，利用数据技术研究股市趋势具有可行性。

目前，关于股市趋势预测的主要研究工作有：文献［1］采用时间序列分析方法训练自回归综合移动平均（ARIMA）、Facebook Prophet 和指数平滑（ETS）模型以预测股市趋势；文献［2］基于深度学习方法训练长短期记忆（LSTM）模型，由于训练特征单一，其模型适应力弱；文献［3］选取多种重要特征，利用随机森林技术预测股市趋势，其预测效果有明显提升；文献［4］将多种技术指标和情绪指标进行融合，以提升预测算法的适应性；文献［5］将基于LSTM 的单变量和多变量模型与文本分析模型相结合，进一步提升了预测算法的适应力，但其股市趋势预测具有明显的滞后性。综上，当前主要的股市趋势预测方法对于股市趋势变化的预测具有滞后性，且预测方法的适应性大多达不到实用性要求。

股市有慢变量和快变量，相对于由每日组成的走势而言，每小时形成的走势是快变量。有研究人员从快慢变量的角度研究股市趋势，如：文献［6］在常用慢变量训练集中加入部分快变量数据，训练出的6 种机器学习模型预测效果有所改善；文献［7］采用回归算法在不同周期的移动平均线上训练，通过预测未来的均线结构判断股市趋势，以提高对于股市趋势预测的灵敏性；文献［8］加大了快变量在训练集中的权重，进一步提高了DRNN-ARIMA 模型的灵敏性。

股票市场中快变量的先行变化对于慢变量的影响过程是一种传动关系，有研究者从传动角度研究股市趋势变化，如：文献［9］通过自回归分布式滞后模型建立实体经济与股市趋势之间的传动关系，进而预测股市趋势；文献［10］使用分位数回归方法研究原油波动率变化对股市趋势变化的传动影响，在一定程度上提升了预测方法的适应力；文献［11］研究拉丁美洲六大股票市场对美国股市趋势的影响，并构建适用性明显提升的MGARCH-BEKK 模型。以上研究工作主要针对外部快变量，研究者也对内部快变量的传动关系进行了初步研究，如：文献［12］根据股价同步性，探究不同周期之间的传动关系，发现不同周期态势具有趋同性［13］；文献［14］通过动态贝叶斯因子图研究宏观经济因子对股市趋势变化的影响，算法适应性有所提升；文献［15］利用贝叶斯网络构建不同周期分时线的结构关系，通过Kuramoto［16］振子模型量化快慢变量间的传动关系，进一步提高了适应力。此外，文献［17］证明了Stuart-Landau［18］振子可以表示任何霍普夫分岔［19］，可以用于研究振子之间的传动过程。

影响图（ID）模型是研究系统结构关系的一种重要工具。文献［20］提出用于建模单个Agent 决策问题的影响图；文献［21］对影响图进行扩展提出多Agent 影响图（MAID），MAID 可以有效地表示多Agent 之间的静态结构关系，但其不能建模动态环境下多Agent 之间的关系；文献［22］结合多Agent 影响图和动态贝叶斯网络，提出多Agent 动态影响图（MADID）模型，实现了Agent在动态环境下的推理。

本文在MADID 模型的基础上引入传动关系，提出多Agent 传动影响图（MATID）模型。通过分析股市不同周期间的影响关系，本文提出一种基于多Agent 传动关系的股市趋势预测方法。首先选取股市的主要趋势性指标，给出指标值的计算方法；然后利用多元线性回归对特征值进行融合；接着引入股市的快慢周期概念，给出快慢周期之间的传动因子计算方法；随后给出MATID 模型的形式化表示，利用股市振子模型描述快慢Agent 之间的传动关系；最后通过联合树自动推理对股市趋势进行预测。本文主要工作如下：

1）通过分析股市中不同周期间的传动关系，给出快周期和慢周期间的传动因子计算方法。

2）在MADID 模型中引入传动关系，提出一种多Agent 传动影响图，以建模快Agent 和慢Agent 之间的动态关系。

3）将Stuart-Landau 振子模型引入到股市的周期Agent 中，利用股市振子模型来描述不同周期Agent间的传动过程。

1 周期能量

股市交易数据具有不同的时间周期，中国股市1 天交易4 h，1 h 有4 个15 min，即股市交易数据可以划分成不同的时间级别。

在不同时间周期下，快周期趋势变化会带动慢周期的趋势变化，这种带动关系是一种传动过程。图1（a）表示上证指数的小时级别，在时间段I 中趋势由下跌转变为上升，在图1（b）所示的日级别趋势图中，在时间段I 中始终为下跌趋势，出现不同周期下走势不一致的现象。在时间段II，传动作用使日周期与小时周期趋势一致。

1.1 趋势性指标值计算

股市主要的趋势性指标包括10 日移动平均线（MA10）、20 日移动平均线（MA20）、指数平滑移动平均线（MACD）和相对强弱指标（RSI）。各指标具体如下：

1）MA10 指标的量化表示

设t时MA10 指标状态用MMA10,t表示，则MA10指标变量X1可表示为：

2）MA20 指标的量化表示

设t时MA20 指标状态用MMA20,t表示，则MA20指标变量X2可表示为：

3）MACD 指标的量化表示

设t时MACD 指标的能量柱状态为MMACD,t，差离线状态为DDIFF,t，差离平均线状态为DDEA,t，则MACD指标变量X3可表示为：

4）RSI 指标的量化表示

设t时RSI 指标的RSI6 线、RSI12 线 和RSI24 线的状态分别表示为RRSI6,t、RRSI12,t和RRSI24,t，则RSI 指标变量X4可表示为：

1.2 指标特征融合

在股市的某一周期下，将MA10、MA20、MACD和RSI 等4 种指标值融合为该周期的能量。周期能量容噪能力强，更易于描述股市快慢周期间的传动关系。

定义1（周期能量）设某周期下的指标状态集合为{X1,X2,X3,X4}，对不同指标值进行融合，融合的结果为周期能量E。

利用多元线性回归模型，周期能量E可表示如下：

其中：a0,a1,…,a4为线性回归系数；ε为随机误差。

通过多维最小二乘法进行无偏参数估计，则有：

2 快慢周期的传动分析

设30 min 级别为快周期，用K 表示，日级别为慢周期，用M 表示。30 min 级别周期能量表示为EK，日级别周期能量表示为EM。

设在t时K 和M 之间的传动因子为λt，传动因子具体表示如下：

K 和M 之间的传动是一个时序过程，给定时间段T=(1,2,…,t,…,n)，K 和M 的传动 关系是每个t时传动作用叠加的结果，K 和M 在时间上的传动关系可描述如下：

其中：λT表示1至n时间段内的传动因子。

在T时间段中，慢周期受到快周期的传动作用力可表示为：

当快慢周期趋势相同时，K 和M 能量变化量同号，λT大于0，慢周期受到的传动力为正，慢周期能量增强；当快慢周期趋势不一致时，K 和M 能量变化量异号，λT小于0，传动力为负，慢周期能量减小。

3 快慢周期Agent 的结构模型

将不同周期分别抽象成不同的Agent，用多Agent 模型建模快周期和慢周期之间的作用关系。

3.1 多Agent 传动影响图模型

MATID 模型结 构如图2 所 示，其 中：St表示t时的状态变量；{s0,s1,s2}分别为St的下跌、横盘和上涨3 种状态分别代表t时快Agent 和慢Agent；Dt表示t时的传 动决策变量；{g0,g1}为Dt的取值，分别表示反向传动和正向传动；Ut表示t时的传动效用结点内部由能量观测结点、决策结点和效用结点UtM构成结构与相同。

图2 MATID 模型结构Fig.2 MATID model structure

一个MATID 模型由概率模型和传动效用模型2 个子模型组成，子模型具体描述如下。

3.1.1 概率模型

设Agent 的行为集{d0,d1,d2}分别代表下跌行为、横盘行为和上涨行为，当传动决策变量Dt根据Agent 行为组合确定传动方式时，可由式（11）转变成随机结点，则Dt的条件概率可表示为：

3.1.2 传动效用模型

传动效用模型是在效用结点中引入股市振子，描述传动关系对Agent 行为和传动方式的影响。

股市振子模型将快慢Agent 分别看作快慢振子，描述快慢振子传动过程中能量的强度波动和相位波动。设快慢振子运动方式为极限环的股市振子模型如式（16）和式（17）所示的股市振子模型与类似。

表1 趋势效用值与趋势行为对照关系Table 1 Contrastive relationship between trend utility value and trend behavior

表2 传动效用值与传动方式对照关系Table 2 Contrastive relationship between transmission utility value and transmission mode

3.2 Agent 间的传动性质

定理1当快慢Agent 行为不一致，快慢Agent的传动因子达到一定阈值时，快Agent 带动慢Agent行为趋势一致。

证明快慢Agent 的传动过程可表示为：

其中：ddS为系统熵增量；ddiS为内部熵增量；ddeS为外部负熵。

在快慢Agent 传动过程中，内部熵增量为慢Agent 能量的变化量根据热力学第二定律，ddiS＞0；外部负熵为快Agent 对慢Agent 的传动力当快慢Agent 行为不一致时，传动因子λT＜0，外部负熵流ddeS＜0。当快慢Agent行为不一致时存在以下3 种情况：

1）|ddiS|＞|ddeS|

当慢Agent 能量变化量大于快Agent 对慢Agent的传动力时，系统熵增量大于0，表示股市正朝着混乱的方向发展。

2）|ddiS|=|ddeS|

当慢Agent 能量变化量等于快Agent 对慢Agent的传动力时，系统熵增量等于0，表明股市处于混乱与稳定的临界状态。

3）|ddiS|＜|ddeS|

当慢Agent 能量变化量小于快Agent 对慢Agent的传动力时，系统熵增量小于0，意味着股市正变得更加稳定。

因此，当|ddiS|≤|ddeS|时，快Agent 带动慢Agent 行为趋向一致，系统由混乱开始变得稳定，此时传动因子为：

因此，定理1 成立，证毕。

4 MATID 趋势预测推理算法

4.1 MATID 联合树构建

定义2（接口）接口是时间片t-1 和时间片t之间有边相连的结点集，时间片t-1 中的接口为It-1，时间片t中的接口为It，则有：

其中：Vi、Vj为结点；Bt为t时间片的网络；Bt-1是t-1时间片的网络；Vts为转移网络的结点集。

定义3（联合树）联合树（JT）是一个二元组(Γ,Δ)，其中，Γ是联合树中团的集合，Δ是连接2 个团之间的分割团集合。对任意一对相邻的团Ci和Cj，Ci∊Γ，Cj∊Γ，Rl∊Δ，Rl为团Ci和Cj之间的分割团，有VRl=VCi∩VCj。

1.5 时间片的联合树是指将t-1 时刻的接口结点和t时刻的全部结点通过正规化、三角化等操作构成一个联合树JTt，图3 所示为MATID 构建的1.5 时间片联合树。

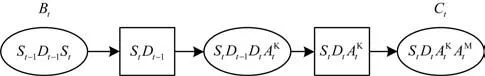
图3 1.5 时间片MATID 联合树Fig.3 1.5 time slice MATID joint tree

在图3 中，团Bt={It-1,Vt}，团Ct={It,Vt}，It-1={St-1,Dt-1}为t-1 时的接 口，It={St,Dt}为t时 的接口。

以接口It-1为分割团，可以将相邻时间片的联合树连接在一起，生成完整的联合树。图4 表示通过接口It-1将JTt-1和JTt连接的联合树。

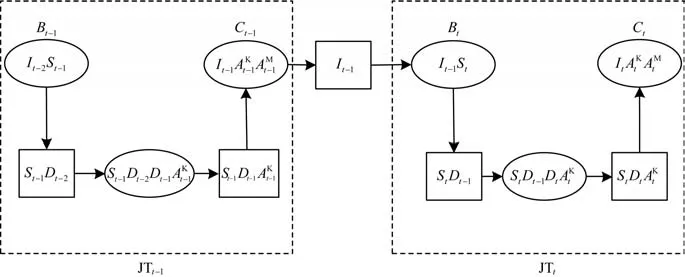
图4 通过接口连接的2 个相邻联合树Fig.4 Two adjacent joint trees connected by an interface

4.2 MATID 的联合树推理

首先构建JTt，初始化JTt中所有团和分割团的条件概率表，对Ct-1进行边缘化操作得到It-1的概率分布；然后吸收快慢Agent 趋势证据与传动证据得到It-1的先验概率其中d1：(t-1)表示快慢Agent 从第1 时间片到第t-1 时间片的行为证据，g1：(t-1)表示第1 时间片到第t-1 时间片的传动方式证据；最后将该概率分布作为先验概率分布乘到Bt的条件概率表上，在JTt中以Ct作为根结点收集证据。

在证据传播到JTt的每个团后，JTt从JTt+1中吸收概率实现对JTt的概率更新。从Bt+1中通过边缘化操作得到It的概率分布然后以Ct作为根结点分发证据，更新Ct的条件概率表，即其中ϕi为团i的概率分布。

当整个网络完成证据传播后，对联合树任意包含St+1的团进行边缘化和归一化，即可得到St+1的后验概率P(St+1|d1：t,g1：t)。MATID 的推理 算法具体描述如下：

算法1MATID 的推理算法

当整个网络完成证据收集和证据分发后，对于目标结点St+1，通过对其所在团的边缘化操作得到后验概率P(St+1|d1：t,g1：t)。

5 实验结果与分析

5.1 数据来源

从上证工业指数中取2016 年5 月17 日—2022 年7月15日的1 500个样本和2010年1月21日—2022年7 月15 日的3 033 个样本，预测未来5 个交易日的趋势。设涨幅大于2%为上涨，涨跌幅在-2%～2%之间为横盘，跌幅小于-2%为下跌。

5.2 评价标准

用精确率（P）、召回率（R）和F1 值（用F1表示）作为评价指标，指标具体描述如下：

其中：TTP是预测为正的正样本；TTN是预测为负的负样本；FFP是预测为正的负样本；FFN是预测为负的正样本。

5.3 模型参数对传动效用的影响

5.3.1 能量调控参数对传动效用的影响

将频率调控参数c设定为1，将能量调控参数β在1～6.8 范围内每隔0.2 设置一次参数，分别针对1 500 个样本和3 033 个样本分析最佳能量调控参数大小与快慢振子之间传动效用的关系，实验结果如图5 所示。

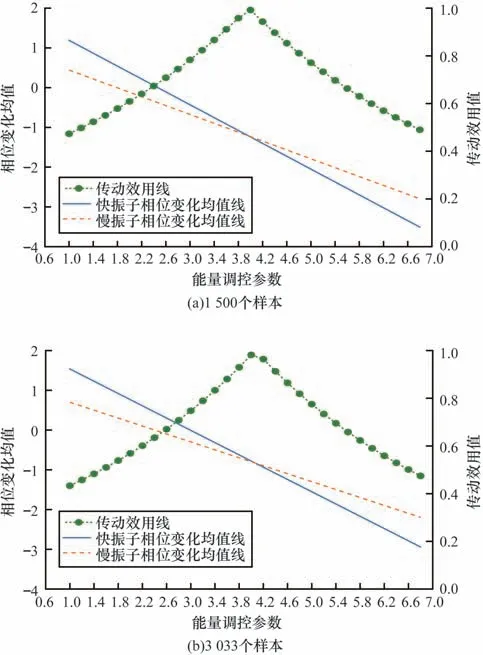
图5 能量调控参数大小对传动效用的影响Fig.5 Effect of energy regulation parameter size on transmission utility

从图5（a）可以看出：在1 500 个样本上，能量调控参数从1～6.8的变化过程中快慢振子相位变化均值单调 减小；相位变化均值差的绝对值φt在1～4之间逐渐减小，同步性增强，在4～6.8 之间逐渐增大，同步性减弱；由可知，在能量调控参数β取4 时传动效用最高。这表明能量调控参数取值与对快慢振子能量的约束力成正比关系，因而快慢振子相位变化均值都呈现下降趋势。振子能量输入不同，振子相位变化均值下降速率也不同，振子之间的φt在交汇处达到最小值，从而取得最大的传动效用值。可见，当β取4 时，Dt正向传动的意愿最强，股市整体趋势趋于同步，符合股市真实情况。

从图5（b）可以看出：在3 033 个样本上，当能量调控参数从1 变化到4 时，同步性增强；从4 变化到6.8 时，同步性减弱；当能量传动参数取值为4 时同步性达到最佳，传动效用达到最大。

5.3.2 频率调控参数对传动效用的影响

根据图5 将能量调控参数取值为4，然后将频率调控参数c从0.3～1.75 每隔0.05 设置一次参数，分析最佳频率调控参数大小对快慢振子之间传动效用的影响，实验结果如图6 所示。

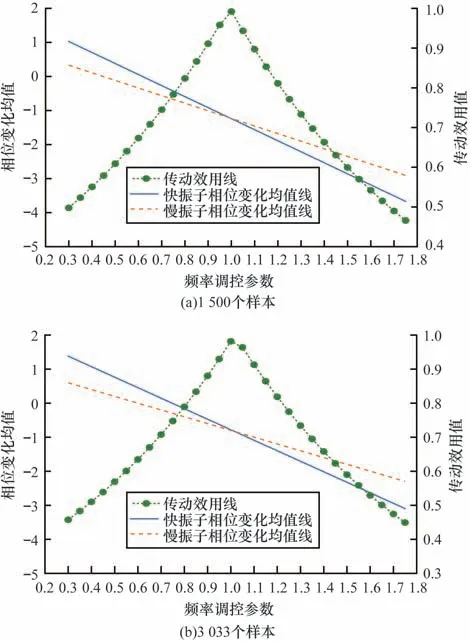
图6 频率调控参数大小对传动效用的影响Fig.6 Effect of frequency regulation parameter size on transmission utility

由图6（a）可知：在1 500 个样本上，频率调控参数从0.3 增加到1 的过程中，快慢振子相位变化均值分别从1.028、0.33 逐渐降低至交汇点-1.236 附近，而传动效用从0.498 上升至0.992；当频率调控参数继续从1 增加到1.75 的过程中，快慢振子相位变化均值和传动效用分别下降到-3.67、-2.906 和0.466；当频率调控参数c取1 时传动效用达到最大值。这是由于频率调控参数与能量调控参数都对能量输入具有约束力，在给定能量调控参数时，增大频率调控参数会更快使得快慢振子之间φt达到最小值，从而取得最大传动效用。

从图6（b）可以看出：在3 033 个样本上，当频率调控参数取1 时，快慢振子之间同步性达到最佳，传动效用达到最大，符合股市真实情况。

5.4 实验对比分析

对不同样本数量和不同趋势阶段分别进行实验，将本文 算法与 门控循 环单元（GRU）［23］、S-LSTM［24］和Hybrid-RNN［25］算法进行比较。在不同样本量和同一个样本量的不同趋势阶段上所得到的结果分 别如表3 和表4 所示，其中，MATID（1）和MATID（0）分别表示在能量调控参数β取4、频率调控参数c取1 的情况下加入传动证据和不加传动证据的实验结果。

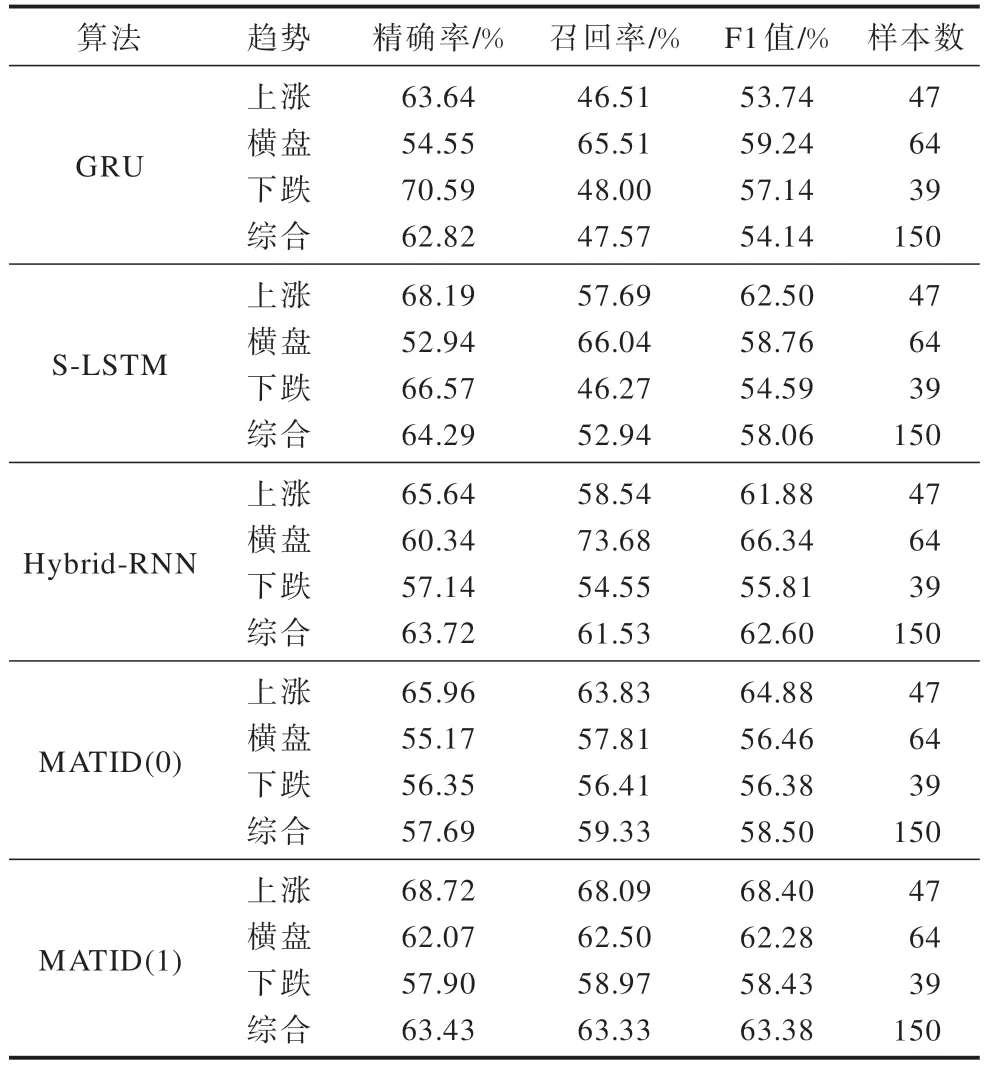
表3 1 500 个真实样本上的算法对比Table 3 Comparison of algorithms on 1 500 real samples

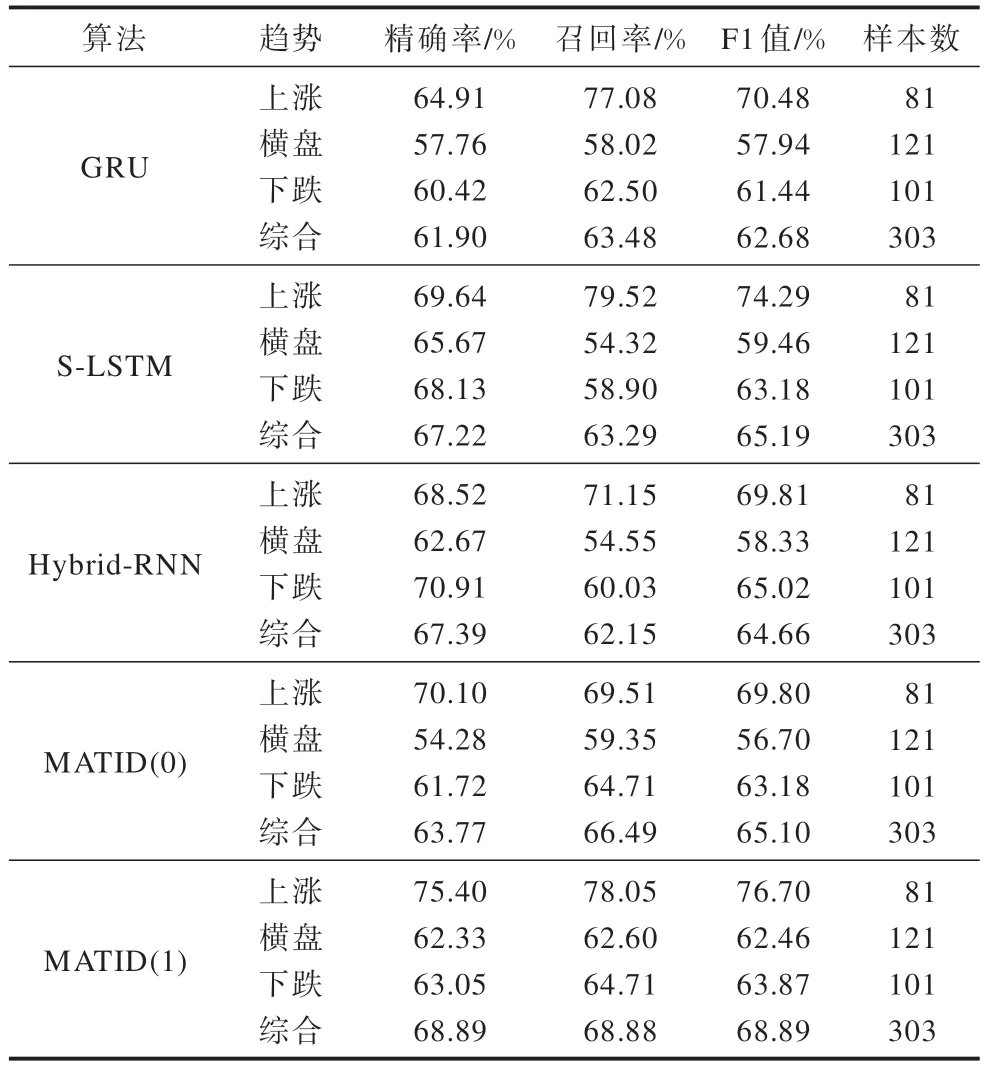
表4 3 033 个真实样本上的算法对比Table 4 Comparison of algorithms on 3 033 real samples

由表3 可知，使用1 500 个样本时，加入传动证据的MATID（1）模型预测效果较好，MATID（1）在上涨和横盘趋势时预测效果明显优于GRU 算法、S-LSTM 算法和Hybrid-RNN 算法，但是在下跌趋势时预测效果一般。综合来看，没有利用快变量数据拟合的模型灵敏性与适应力较差，加入传动证据的MATID（1）模型预测效果优于对比的3 种算法。

由表4 可知：GRU 算法在精确率上表现一般，在召回率与F1 值上有明显提高；S-LSTM 算法在召回率与F1 值上都有明显提升；Hybrid-RNN 算法在预测下跌趋势时效果较好，但整体预测效果一般；MATID算法在预测上涨和下跌趋势时都有显著提高，横盘趋势下的预测效果也有一定提升。加入传动证据的MATID（1）以平均68.89%的F1 值明显优于GRU 算法、S-LSTM 算法和Hybrid-RNN 算法，具有较强的灵敏性与适应力。

为了进一步分析传动证据对实验结果的影响，在3 033 个样本的3 种趋势中分别随机选择40 个样本，将MATID（0）和MATID（1）算法的预测值与真实值进 行对比 并绘制ROC 曲线［26］，如图7、图8所示。

图7 3 033 个样本中3 种趋势下的预测值与真实值对比Fig.7 Comparison of predicted values and true values under three trends in 3 033 samples

图8 3 种趋势下的2 种算法ROC图Fig.8 ROC charts for two algorithms under three trends

由图7 可知：在上涨趋势第8 交易日、第22 交易日和第37 交易日，在横盘趋势第5 交易日、第20 交易日、第37 交易日、第40 交易日，在下跌趋势第19交易日、第23 交易日，加入传动证据的模型预测结果比未加传动证据的模型结果更加准确。

从图8 的ROC 曲线可知：加入传动证据的MATID（1）的AUC 值比不加传动证据的MATID（0）的AUC 值更高。

由表3、表4、图7 和图8 可知，加入传动证据的模型比不加传动证据的模型预测效果有着明显提升，特别是在横盘趋势下，加入传动证据后预测效果提升更加显著，模型灵敏性与适应力也明显增强。因此，加入传动证据可以提高模型的灵敏性与适应力，在复杂情况下算法也具有较好的稳定性。

6 结束语

股市趋势预测具有实际意义，本文从快周期和慢周期的先后关系入手，研究快慢周期的传动作用对于股市趋势的影响。通过将多Agent 动态影响图与传动关系相结合，提出一种多Agent 传动影响图模型。选取主要的趋势性指标，并将这些指标融合为相同周期下的能量特征，以降低噪声；根据周期能量指标变化量的不同给出传动关系的表示方法，利用多Agent 传动影响图建模快慢Agent 的传动结构关系，并融合股市振子模型描述快慢Agent 的传动过程，在传动决策结点上显式体现传动方式；通过联合树推理技术研究历史数据中快慢Agent 之间的传动作用对股市趋势的影响。实验结果验证了该模型的可行性和高效性。考虑到传动因子达到阈值时Agent 行为会发生改变，因此，下一步将研究传动因子阈值与股市趋势变化临界性之间的关系。