“学习进阶”视域下的数学单元复习课模式探索——以“勾股定理”的单元复习为例

⦿ 江苏省海安市紫石中学 彭 鹏

数学学习是一个螺旋上升、不断进阶的过程,学习者在各个学习阶段有着不同的具体学情,也有着不同的学习目标.而“学习进阶”理论作为一个教育学概念,则是基于学习者以上学习事实而提出的,倡导让学习者的数学学习从低阶走向高阶、从模仿走向创新、从现象走向本质,以实现高阶思维的培养和数学核心素养的发展,彰显数学学科的育人价值[1].

单元复习课对于日常数学教学而言基础且重要,原因在于其承载着梳理知识、完善结构、培养思维和发展素养等多重任务.然而一些教师为了完成教学任务,常常倾向于大容量、高难度和快节奏,这种教学模式以教师讲、学生听为主,难以调动学生复习的内驱力,弱化了知识的重建、结构体系的再构建及思想方法的再优化,无法让数学学习走向高阶.

事实上,复习课在实践“学习进阶”理论中具有较大优势.下面笔者以“勾股定理”的单元复习为例,说明“学习进阶”视域下的单元学习活动设计,以飨读者.

1 “学习进阶”下的课前思考

作为平面几何中的重要定理之一,“勾股定理”不仅揭示了直角三角形三边的数量关系,而且是渗透数形结合思想的有效载体.基于对新课标的分析,笔者认为本节课的进阶起点大致如下:对勾股定理及其逆定理的内涵、相互关系有一定的认知基础,并能解决一些简单的实际问题.据此,教师可以围绕进阶起点设定进阶目标[2].

当然,本节课的学习进阶由于各种具体学情,存在如下障碍:(1)受到新课学习中诸多因素的影响,如时间紧导致勾股定理及其证明不够充分,时间久导致定理证明的遗忘等,使得不少学生“只知其然”;(2)由于学生缺乏在复杂情境中探寻隐含关系的能力,使得本节课的学习进阶困难重重;(3)学生思考和表达能力方面的欠缺,使得后续解决立体图形表面“最短路径”问题落入困顿的境地.同时,如何融通定理内涵与爱国情怀,培养学生的实践能力和合作意识等都是本节课的难点.

2 “学习进阶”理论下的教学设计

2.1 情境导入,融入学习

问题1图1是耸立于萨摩斯岛的毕达哥拉斯雕像,从中你能生成什么数学联想?(课件呈现图1,学生很快据图抽象出“直角三角形”,并引出其性质等.)

图1

设计意图：通过数学史素材设计一个问题,一方面引领学生温故知新,让学生沿着知识台阶与思维起点探索,沿着精准进阶路径前行;另一方面,通过素材为后续勾股定理的进阶认识打下伏笔.

2.2 自主检测,进阶起航

教师共出示五个习题(此处由于篇幅有限,具体习题略).

设计意图：通过拾级而上的五个问题,考查定理本身及其几何意义、逆定理的应用及勾股数,强调定理本身的内涵,综合应用定理及其逆定理;通过“赵爽弦图”证明定理,助力学生自主整理知识,完成自主梳理和思维进阶.同时,教师在巡视中了解学生的进阶起点,为学生后续的进阶学习设计科学而适切的路径.

2.3 踏梯而上,逐层进阶

问题2如图2,一根竹子原高一丈(等于10尺),一阵风来竹子折断,竹稍恰好抵地,且抵地处距竹子底部6尺,试求折断处距离地面的高度.(出自“折竹抵地”问题.)

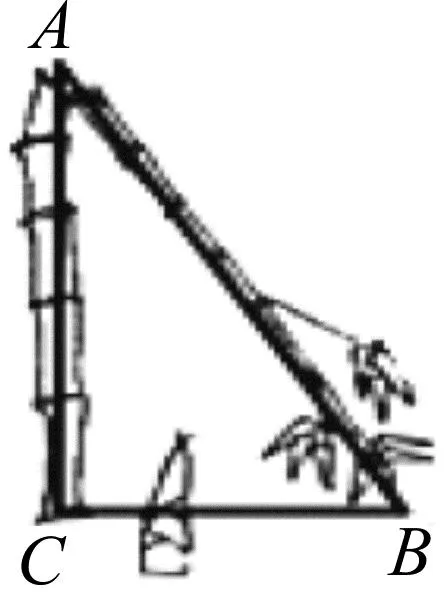
图2

问题3如图3,已知一池塘的截面为正方形,其边长10尺,池塘中央长着一棵芦苇AB,高出水面的部分BC长1尺.若把AB沿着与水池边垂直方向拉向岸边,则该芦苇顶部B刚好碰到岸边的B′处,试求水深及芦苇的高度.

图3

问题4在图4所示的直角三角形纸片ABC中,已知AC=6 cm,BC=8 cm.若将边AD沿着AB折叠,使其落于斜边AB上并与AE重合,求线段CD的长度.

图4

问题5在图5所示的长方形ABCD中,已知AB=16,BC=8.若沿着AC折叠矩形ABCD,使得点D与点E重合,且CE交AB于点F,求线段AF的长度.

图5

问题6图6所示的长方体木块的长、宽、高分别为4 cm,3 cm和4 cm.已知一只蜘蛛藏匿于木块的一顶点A处,一苍蝇停在与蜘蛛相对的顶点B处.若蜘蛛想沿着最短的路线捕获苍蝇,则需沿着什么路线爬上去?最短路径的长是多少?

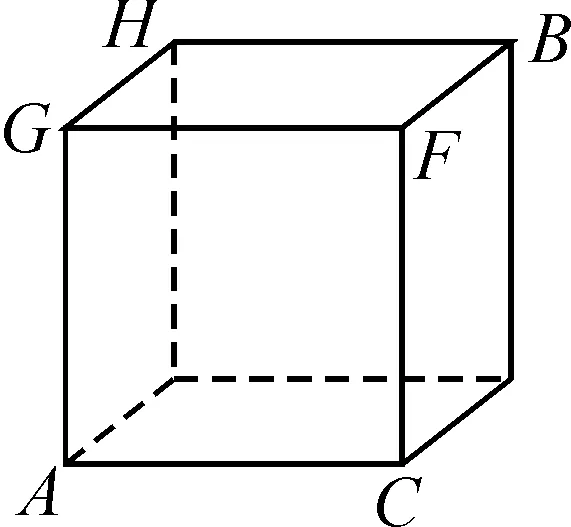
图6

设计意图：在这一环节,教师以不同层次的多个问题进行引导,以例题与变式相结合的方式,逐级提升问题难度,让学生通过自主探究、小组讨论和合作交流分析与解决问题,培养数学思考、语言表达和数学探究能力,使思维品质与理性精神得到最大限度的发展.在学生解决问题6之后,教师继续从“立体图形表面最短路程”角度提出变式问题,如蚂蚁爬圆柱表面、爬多级台阶等,让学生充分想象和思辨,以发展直观想象能力和数学思考能力.此处将勾股定理模型贯穿整个环节,使学生学习的积极性越发高涨,让数学学习越发深入.

2.4 课堂小结,深化学习(略)

2.5 课后进阶,升华课题

问题7“勾股定理”看似简单,却有着深刻的寓意,下面请大家从以下课题中选择一个以小组合作的方式研究:

(1)“勾股定理”的历史;

(2)整理“勾股定理”的证法(不少于8种).

问题8各小组围绕如下话题试着制作一张专题手抄报:

(1)古今中外数学家研究勾股定理的有趣故事;

(2)具体介绍搜集的勾股定理验证方法中的一种;

(3)以上课题学习中你的收获与困惑.

设计意图：本章节知识中囊括了丰富的德育元素,为教师的“立德树人”价值追求提供了契机.在这一环节中,教师鼓励学生以小组合作的形式展开研究性学习,更加深入地了解勾股定理的发展史和各种证法,并以手抄报的形式展示成果,水到渠成地培养学生的爱国情怀与科学精神.当然,由于课堂学习时间有限,本环节可以延伸到课后,使学生的深度学习不断延伸开去.

3 几点思考

3.1 以“立德树人”为统领

数学知识是人类文明的产物,承载着各种思想与文化,一线教师需自觉将“立德树人”的目标落实在具体的教学之中.在本课中,教师以“立德树人”为统领,针对性地将其列为学生学习进阶的延伸点,通过“一针见血”的设计与引导,提升数学复习课的育人价值,以文化力量厚植学生的爱国情怀,水到渠成地提升学生数学核心素养.

3.2 以“明暗相交的目标”为主线

数学学习需要落实知识技能与学科素养双重层面的目标,这就需要教师基于这两个层面分别设计“明暗相交”的进阶目标,让学生在渐次提升的问题情境中深度思考、探究和交流,最终实现学习的自然进阶.在本节复习课中,教师的教学设计呈现多个水平层次,让学生在低起点、高立意的数学探究进程中获取数学知识技能,发展数学思维,提升数学素养[3].

3.3 以“问题链”为载体

数学复习课应以问题为纽带,以知识的发展与思维的培养为主线,以师生、生生互动的形式形式提高学生学习的参与度,增强数学思维的层次性,提高复习课的质效.本课中教师基于学习进阶目标精心选题改编,并以“问题链”为载体,引导学生独立探索和互动研讨,使学生的思考脉络得到递进式发展,促进数学素养的自然提升.