纠错型小结设计的教学策略浅析

⦿ 江苏省高邮市南海中学 倪开磊

初中阶段的数学知识难度逐渐增加,学生在接受丰富的数学知识的同时,思维能力的提升仍不尽如人意,在运用数学知识的过程中常常会出现各种错误.这些错误反映了学生在思维上的缺陷以及对知识的认识还不够深刻,是学生真实情况的反映,也是进行精准教学的基础.因此,在教学中要妥善利用这些错误,让学生直观地认识到错误的原因,在思维上得以纠正,真正理解数学本质[1].笔者以纠错型小结为主题,结合教学实践,谈一谈在教学中的设计与思考.

1 在对比辨析中纠错

新知的学习建立在学生已有的知识结构基础上,因此,可以充分运用新旧知识之间的联系进行正向迁移,使新知的学习更加顺利.同样也可以将新旧知识进行对比和辨析,使学生在明晰新旧知识区别的基础上正确认识学习过程中出现的错误,从而锻炼思维能力,纠正学习过程中出现的思维偏差.

案例1“反比例函数的图象与性质”纠错型小结

下面的说法正确吗?请说一说你的理由.

函数体现了数形结合思想,在综合性试题中的应用非常广泛,也是学生学习中的一个难点.本例中通过比较反比例函数和一次函数的图象与性质,学生对两种函数图象有更加清晰和准确的认识,能够明确二者之间的区别和联系,从而准确把握两种图象的特点,在解题时能够更加灵活加以运用,精准解题,掌握这一类试题的本质规律.

2 在展示典型中纠错

课堂小结是将学生在本节课中学习的知识和解题方法进行归纳和梳理,在展示典型中纠错,也就是引导学生换一个新的角度进行知识回顾,这样一来,既避免了知识的零碎和杂乱,也回避了课堂小结中学习内容的简单重复,激发学生的学习兴趣,使教学起到提炼和升华的作用,最终促进知识体系的建构.

案例2“二次根式”的纠错型小结

教师将学生在本课学习中的典型错误进行了汇总,请学生分析错误的原因.

在小结中直接呈现学生的错误,使学生受到直接的感官刺激,从而对这一解题过程中应该引起注意的事项产生更加深刻的记忆,能够更好地提升解题的技能,强化对知识的理解.

3 在解析阐释中纠错

实验操作是学生通过亲自动手实践,在活动中增强自身感受、掌握知识、体悟思想的过程.实验操作能够强化学生对知识的认识,了解知识推导的过程,真正产生深刻的理解.在实验操作中引导学生解析阐释,通过活动验证数学的性质和定理,促使学生理解数学的解题方法.

案例3“等腰三角形的轴对称性”纠错型小结

如图1,学生小明从一张纸片上(非等腰三角形)剪出一个等腰三角形,他将点A沿∠C的角平分线CD折叠,使点A落到BC边上的点E处,沿着线段DE剪去△DBE.小明认为将剩下的图形展开,就可以得到一个等腰三角形.

图1

师:请问小明的操作方法可以得到一个等腰三角形吗?如果不能,你觉得应该如何操作才能得到一个等腰三角形呢?

…………

本例中的小结给学生提出了一个思考性的问题,需要学生思考如何折纸才能得到一个等腰三角形,并且要思考小明的折法为什么不能得到一个等腰三角形.在解决这个问题时,可以把AB边上的高作为对称轴,将△ABC沿着这一对称轴折叠,使点A落到AB边上的点F处,沿着线段CF就可以剪出等腰三角形AFC.另外,还可以利用高和角平分线合一的方法剪出一个等腰三角形.以上案例中,通过亲自动手折纸、剪纸,学生对等腰三角形的轴对称性产生了直观的认识,培养了空间想象能力.

4 在解析应用中纠错

学会应用数学知识是学习的目标之一,因此,在教学中要引导学生运用数学知识解决具体的实际问题,在解决问题中学会知识的迁移.设计知识应用式纠错型小结,能够提高学生在具体情境中应用知识的能力,还能培养学生的应用意识,使其认识到数学知识的价值,提高解决问题的技能.

案例4“分式方程”的纠错型小结

学校食堂要去菜市场购买食材,第一天花了60元购买青菜,第二天又买了同一种青菜,花了75元,第二天菜价下跌,每千克比第一天便宜了1元钱,结果第二天比第一天多买了5千克青菜.假设第一天买了x千克的青菜,请根据题意列出方程.

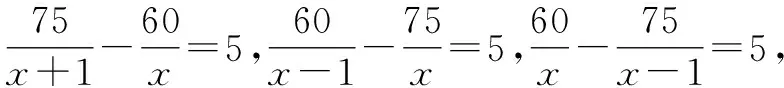
本例中教师将学生的错误进行展示,并且师生共同讨论分析,帮助学生认识到错误的原因,从而更加有效地认识到运用分式方程解决问题时应该注意的关键问题,厘清列分式方程的各种要素.

5 在探究错例中纠错

拓展延伸是基于学生的认知水平对所学内容进行的合理拓展,这一过程丰富了学生的知识储备,锻炼了学生的思维能力.在此过程中设计纠错型小结,可以帮助学生深度理解知识,培养探究能力[2].探究性错例设计一般可以在复习课堂上使用,能够有效提升学生综合运用知识的能力,积累探究经验,深度理解数学本质.

案例5七年级上册期末复习纠错型小结

A,B是数轴上的两个点,分别表示数a和b,那么A,B两点之间的距离可以表示为|a-b|.

(1)假设数轴上的两个点A,B分别表示的是数x和-1,且线段AB的长为2,你觉得x的值为多少呢?学生甲认为x=1,你觉得对吗?说一说你的理由.

(2)当x的值为多少时,代数式|x+1|+|x-3|能够取到最小值?学生小明经过举例验证,分别使x等于-7,-5,-3,1,3,5,7计算代数式的值,发现x的值为1和3时,代数式|x+1|+|x-3|的值最小,因此,小明认为要使代数式|x+1|+|x-3|取最小值,x的值应该为1和3,你觉得这个说法对吗?说一说你的理由.

本题是七年级上册期末复习时的典型例题,重点需要学生能够将所学知识进行综合运用,梳理知识体系,形成系统的解题方法和策略,全面提高数学思维品质.本例将绝对值的相关知识、加减运算和简单的一元二次方程相结合,增强了问题的综合性和挑战性,学生在思考这两个问题的时候都出现了思维不够全面的问题,出现了一些错误.通过展示这些错误,引导学生通过数形结合的方式综合考虑这类问题,使其学会分类讨论,更加全面地思考和分析问题,提高解题的正确率.

总之,在课堂结束总结阶段或者复习教学时采用纠错型小结,可以发挥典型错误的警示和教育功能,使学生能够更加深刻地认识错误原因,抓住问题的本质,为正确解答问题奠定基础[3].教师要基于学情有效设计纠错型小结,改善教学方式,有效提升教学效率,促进高效课堂的生成,落实学生的核心素养.