基于问题驱动下的课堂教学设计与思考——以“分式方程”教学设计为例

⦿ 江苏省苏州市彩香实验中学校 陆 娴

问题是思维的起点,是数学教学的核心.在“分式方程”教学中,教师紧贴学生实际设计问题,让学生在问题的引领下理解并掌握分式方程的相关概念,归纳总结解分式方程的一般步骤,让学生的思维能力和探究能力在问题的引领下螺旋上升.

1 教学分析

1.1 教材分析

分式方程是整式方程的延伸和发展,其解法比整式方程更加复杂.教学中,教师应重视引导学生观察分式方程的特点,并有意识地引导学生与一元一次方程相对比,探寻解分式方程的基本思路,领悟分式方程与整式方程在解法上的内在联系,提高学生发现、分析和解决问题的能力.

1.2 学情分析

在学习分式方程前,学生已经掌握了分式的概念、基本性质及相关运算,同时学习了整式方程,并积累了丰富的解题经验,这些知识、经验等为分式方程的学习提供了前提和保障.

2 教学设计

2.1 创设情境

问题1植树节,学校组织甲、乙两班学生参加植树活动,乙班每小时比甲班多种1棵,甲班种20棵树的时间与乙班种24棵树的时间相同.怎样描述蕴含其中的等量关系?

该题具有一定的开放性,教师预留时间让学生独立思考.从教学反馈来看,学生给出了不同的解决方案,教师投影展示.

设计意图：从现实生活情境出发,引导学生用方程描述其中蕴含的等量关系,体会方程是刻画现实生活的重要模型.结合已有知识和已有经验,学生建立不同类型的方程,为新知的学习准备了充足的素材.

问题2上述方案中哪些方程是我们学过的?哪些是我们没有学过的?它们具有怎样的结构特点,与我们之前所学的哪些知识相关联?

设计意图：引导学生通过直观观察发现分式方程的分母含有未知数,并结合学生的回答逐步画出方程的联系图,有效沟通旧知与新知的联系.

问题3你是否能够写出一个符合以上特点的新方程?

设计意图：通过创造让学生进一步理解分式方程的结构特点,进而为分式方程概念的得出作铺垫.

问题4若想给此类方程起个名字,你想叫它们什么呢?

设计意图：引导学生将新方程与整式方程和分式相比较,进而给新方程命名为“分式方程”.这样引导学生经历概念抽象及方程的命名过程,让学生体会“创建”知识的成就感.结合以上分析,此时给出分式方程的概念自然也就水到渠成了.

2.2 探求新知

问题5以下方程是整式方程的是______;是分式方程的是______.(请将序号填写在横线上.)

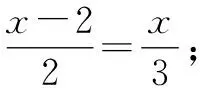
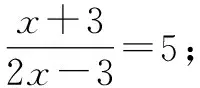
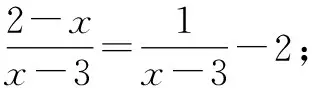
设计意图：通过辨析进一步深化学生对分式方程概念的理解.在此过程中,不仅要关注结果,还应引导学生对比,发现不同类型方程之间的关系,以此为接下来探究分式方程的解法作铺垫.

问题6知晓了分式方程的概念,接下来该研究什么呢?

设计意图：根据已有经验,自然给出下一步研究内容——解分式方程.这样在问题的驱动下,启发学生整体把握学习内容,通过旧知迁移掌握新知探究之路.

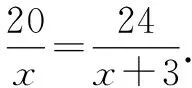
虽然分式方程是新学内容,但是分式的概念及整式方程的解法是学生非常熟悉的.因此,在求解过程中,教师没有直接给出解题过程,而是预留时间让学生自主探究.

设计意图：改变以往“讲授+模仿”的教学模式,预留充足的时间让学生结合已有知识和已有经验探寻解题之路.在教师的启发和指导下,学生思考“要做什么,为什么这样做,依据是什么”,以此通过亲身经历方法的探究过程,理解并掌握分式方程的解法.

问题8说一说你的解题思路?

教师可以继续给出几个分式方程让学生独立求解,然后板演详细的解题过程,并让学生通过对比分析归纳出分式方程求解的基本思路和具体做法,以此规范解答.不过,在此过程中,对于“检验”这个过程可以先留白,后面通过深入探究来突破“检验”这一难点.

设计意图：引导学生进行对比分析,得出在解分式方程时,可以通过“去分母”将分式方程转化为整式方程,进而利用整式方程的解题经验解决问题.

2.3 拓展延伸

设计意图：通过具体操作帮助学生进一步熟悉解分式方程的基本思路.在解题过程中,教师要启发学生继续思考如何去分母,如何找到最简公分母,同时提醒学生在去分母时不能出现遗漏.

问题10你的计算结果是什么?观察计算结果,你有什么发现?

设计意图：通过去分母将其转化为整式方程,解得x=3.学生认真观察、分析,不难发现问题——x=3时,方程无意义.由此引发认知冲突,此时增根的概念呼之欲出.

问题11分析问题9的解题过程,你认为解分式方程应该增加一个什么环节?

设计意图：在教师的启发和引导下,学生体会到检验在解分式方程中的重要性,从而真正理解增根的意义.

问题12结合以上解题过程,你能总结归纳解分式方程的一般步骤吗?

设计意图：引导学生通过归纳总结,得到解分式方程的一般步骤.(1)化分式方程为整式方程;(2)解整式方程;(3)检验方程的根;(4)写出计算结果.这样通过总结归纳,帮助学生形成清晰的认识,解分式方程自然可以得心应手.

2.4 巩固练习

问题13解下列方程:

设计意图：借助练习帮助学生巩固解分式方程的步骤,提高学生的解题技能.同时,通过精选练习让学生进一步体会检验在解分式方程中的价值,有效规避因忽视检验而产生错解的风险,培养思维的严谨性.

2.5 课堂小结

问题14通过本课的学习,你学会了哪些知识?还存在哪些问题?

设计意图：教师先让学生自己总结归纳,然后进行生生和师生互动交流,以此通过思考与交流进行知识梳理和总结,逐渐完善学生的认知结构,让学生深刻理解并掌握解分式方程的一般步骤.

3 教学反思

3.1 借助问题,引导学生经历概念形成过程

数学概念是数学知识体系的核心内容,学生对概念的理解程度,直接关系着学生的认知水平.概念教学中,教师不应直接将结果呈现给学生,应该引导学生经历概念的形成过程,以此揭示概念的本质,促进概念的深化.

3.2 借助问题,提升学生自主探究能力

课堂教学是动态变化的,教学中既要关注预设,还要重视生成.在实际教学中,教师要结合教学实际精心设计问题,让学生在问题的引领下积极思考、主动交流,以此成就精彩的课堂生成.而教师作为课堂教学的组织者、启发者和引领者,要及时捕捉有效的信息,并将其转化为宝贵的教学资源,以此通过合理的开发与利用,帮助学生形成正确的意识,提升学生的认知水平.

总之,在数学教学中,教师要认真研究教材、研究学生,结合教学内容和学生实际学情设计一些有意义的问题,让学生在问题的引领下,学会发现、学会探索、学会抽象,以此提高认识水平,提升数学素养.