核心素养视域下的单元教学——以“运算律”单元教学为例

江苏宜兴市城北小学（214200） 薛彩霞

在核心素养视域下，以主题引领单元教学，要做到：1.目标制订，建立核心素养导向的学习目标，选择与主题相匹配的核心素养表现；2.主题确定，结构化整合教学内容，遵循数学学科逻辑和学生学习逻辑；3.解决问题，综合本学科知识和方法运用，综合运用数学与其他学科的知识和方法解决实际问题。另外，在教学中还要遵循学生的认知规律，不断调整和优化主题探究的进程，以此促进数学课程育人方式和学生学习方式的变革。

运算律，即运算的规律。加法和乘法的计算过程蕴含着具有普遍意义的规律。在计算过程中，学生可以通过演绎推理，将这些规律运用于具体计算。在运算律的教学过程中，教师要引导学生关注数学深层次的潜在结构，并用符号表达这种具有一般性的规律，以提升学生数学思维能力。

一、单元内容分析

“运算律”单元内容及相关内容见表1。

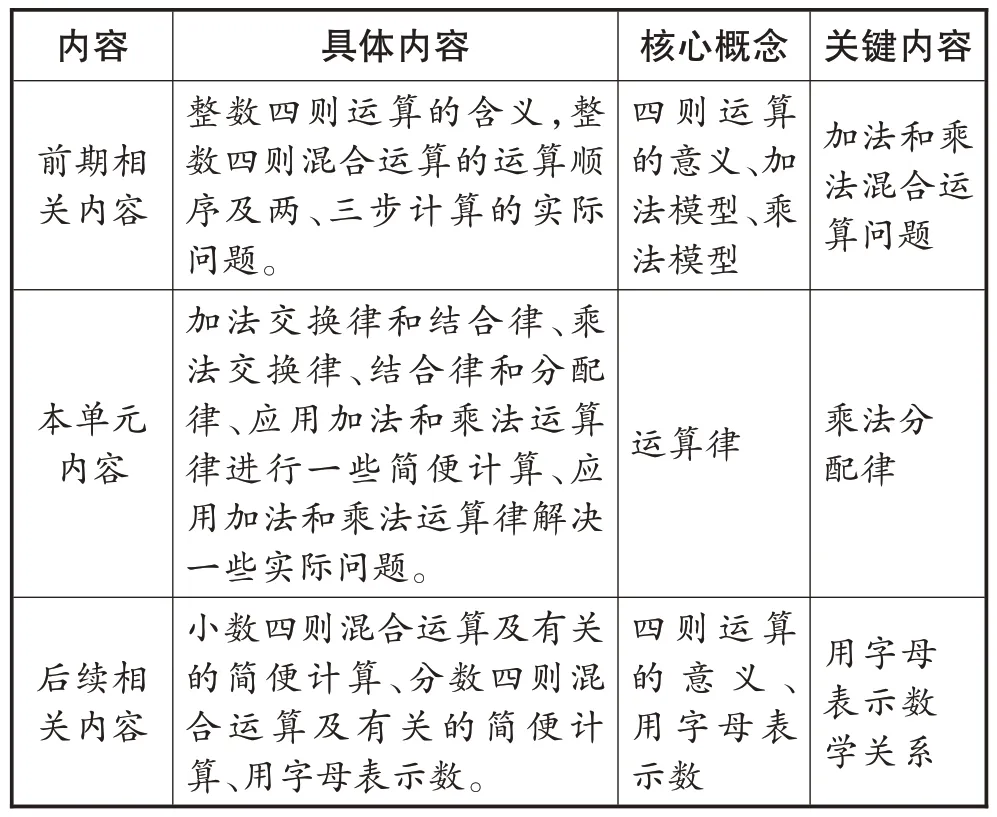
表1 “运算律”单元内容及相关内容

（一）目标制订指向核心素养

《义务教育数学课程标准（2022 年版）》（以下简称《课程标准》）对运算律的内容要求是：探索并理解运算律（加法交换律和结合律、乘法交换律和结合律、乘法对加法的分配律），能用字母表示运算律。以此为基础，基于“教—学—评”一致性教学理念，笔者从学业要求、具体表现、素养指向三个方面，制订了单元学习目标（见表2）。

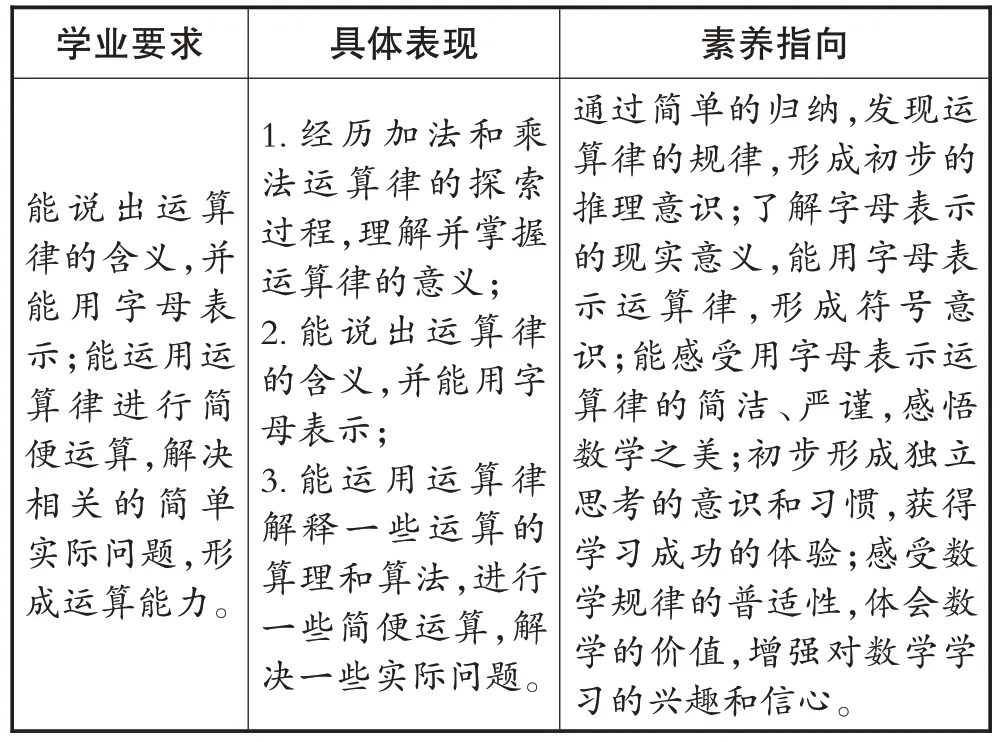
表2 “运算律”单元学习目标

对学业要求，从“教”的角度入手，明确学生需要掌握的知识技能；对具体表现，从“学”的角度入手，细化学生探究的具体行为表征；对素养指向，从“评”的角度入手，掌握学生学习过程中核心素养的具体表现。单元学习目标从学业要求、具体表现、素养指向三个方面进行分析解读，更具体、操作性更强，让教师的“教”和学生的“学”更适切。

（二）教学内容结构化整合

基于儿童立场，由“生活逻辑”和“学科逻辑”生成“学习逻辑”。笔者依据课程标准理念和课程内容，设计单元主题“寻找算式中的小秘密”（如图1），并将单元主题进行拆解，降低学生的学习难度。

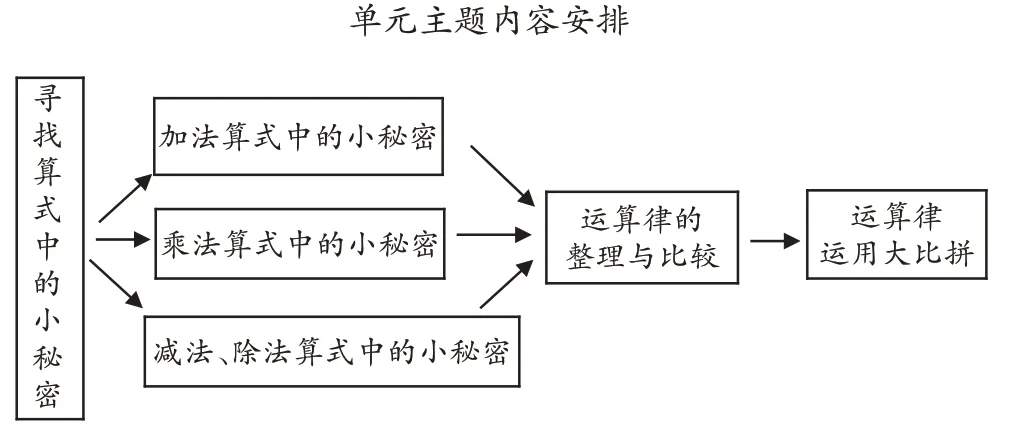
图1

通过主题引领，整体建构单元知识，并通过对学习过程的回顾反思，促进学生形成对核心知识和学习历程的深刻理解，培养学生解决问题、沟通与合作等重要能力，发展学生的批判性思维。

（三）主题引领情境化设计

《课程标准》对运算律内容的教学提示是：通过实际问题和具体计算，引导学生用归纳的方法探索运算律、用字母表示运算律，感知运算律是确定算理和算法的重要依据，形成初步的代数思维。

笔者在教学中利用校外实践基地“开心农场”，结合“寻找算式中的小秘密”这一单元主题，通过信息技术的运用，创设农场探险活动情境。通过开展农场探险活动，让学生在合作探究中，进行深入持续的规律探索，在富有挑战性的情境活动中，调动现有的知识、能力、经验等创造性地解决问题，从而达到培养学生核心素养的目的。

二、教学实践

（一）经历“猜想—验证”的过程，使推理有序

运算律的学习过程通常是：解决一个实际问题—看到一个数学现象—进行类似的试验推理—从众多案例中抽象概括—用符号表示所发现的规律。以加法交换律为例。

1.学习例题，初步发现问题

师：操场上有28 个男生跳绳，17 个女生跳绳，23个女生踢毽子，一共有多少人跳绳？

生1：28+17=45（人），一共有45人跳绳。

生2：17+28=45（人），一共有45人跳绳。

师：这两个算式有什么关系？

生3：结果相等。

2.小组讨论，说理“相等”

师：用多种方式证明28+17=17+28。

生4：可以结合实际问题来证明。28+17和17+28都是求跳绳的人数，所以两个算式的结果相同。

生5：可以通过计算证明。因为28+17=45，17+28=45，所以28+17=17+28。

生6：可以通过画线段图（如图2）来证明。

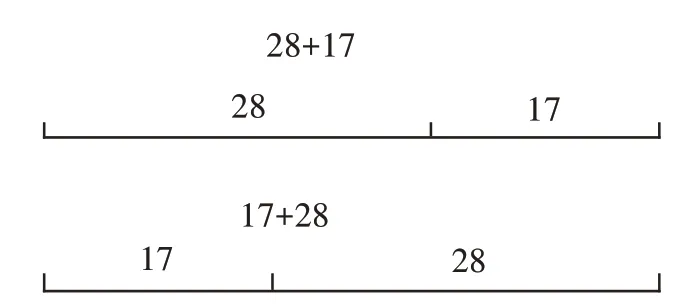
图2

生7：可以利用加法的意义来证明。算式28+17 和17+28 都是求28 和17 合起来是多少，所以28+17=17+28。

3.举例对比，总结规律

师：照样子写出其他类似的算式，观察比较这些算式，你有什么发现？把你的发现用喜欢的方法表示出来。

……

通过自主探索、对比研究，学生深刻认识了加法交换律。在教学中，教师给学生留出自主探索、合作交流的时间与空间，借助丰富、有趣、高效的学习活动，引导学生充分观察、比较、归纳、类比，有助于学生积累研究经验、培养推理意识、提升思维能力。

（二）多种方式验证规律，让推理有据

如何让抽象的思维具体化、形象化？这需要教师从数学知识的本质出发，引导学生通过数形结合的方式理解知识，降低学习难度。以乘法分配律为例。

1.以问题引导反思

（教学乘法分配律后，教师引导学生对学习过程进行回顾反思。）

师：不计算，怎样证明（5+2）×3=5×3+2×3？

2.小组合作，多角度思考

组1：可以利用乘法的意义来证明。左边算式（5+2）×3 表示7 个3 相加，右边算式5×3+2×3 表示5个3 加2 个3，实际也是7 个3 相加。两个算式都是求7个3是多少，所以结果相同。

组2：可以画图证明（如图3）。两个算式都是求圆片的总数，故两个算式相等。

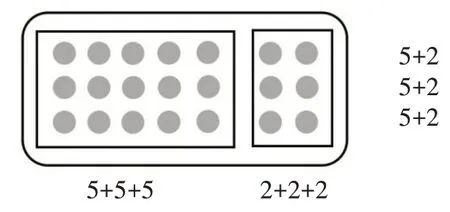
图3

组3：可以用长方形的面积来证明。长5厘米、宽3 厘米的长方形和长2 厘米、宽3 厘米的长方形的面积之和，与将这两个长方形拼成一个长7 厘米、宽3 厘米的长方形的面积相等（如图4），故（5+2）×3=5×3+2×3。

图4

通过“观察—猜想—验证”这一过程体会乘法分配律，学生对乘法分配律的理解并不深刻。对此，教师可以进一步提出问题，让学生通过小组合作，借助已有经验，发挥创造力和想象力，从乘法的意义、数形结合等角度，进行验证。通过数与形的碰撞，可以使学生巩固对乘法分配律这一抽象数学规律的认识，深化学生对其本质的理解。

（三）回顾反思解读算理，提升思维

运算律是整数加法和乘法计算法则的推理依据。学习中，计算教学在前，运算律教学在后，计算方法没有从运算律进行推理。在教学运算律后，教师可以借助运算律，引导学生对已经学习过的计算法则进行再认识，促进学生对计算法则形成更深层次的理解。以乘法分配律的回顾反思为例。

师：在之前的学习中，哪些知识应用过乘法分配律？

生1：在两位数乘一位数时有用过，如72×6 的笔算（如图5），把72 各数位上的数依次与6 相乘，依据的是乘法分配律。

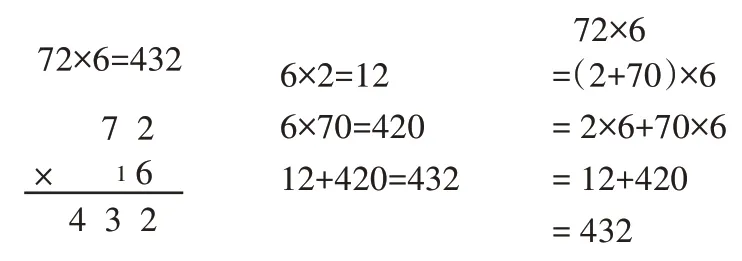
图5

生2：在三位数乘两位数时也有用过，如128×16 的笔算（如图6），先把128 各数位上的数依次与16 各数位上的数相乘，再把两次的计算结果相加，依据的也是乘法分配律。

图6

通过回顾，学生经历了用运算律解释以往熟悉运算的算理和算法的过程，并通过数学图式和语言解读，体会到运算律是运算的固有规律，是确定算理算法的重要依据，加深了对运算律的理解，形成了初步的推理意识。

（四）绘制思维导图，完善知识结构

知识是由符号表征、逻辑形式和意义三个内在要素相互关联组成的。学生学习的过程就是将“知识”作为素材，通过感知与理解、抽象与迁移、体验与感悟，完成自身的知识体系的架构，实现自身的成长与发展。绘制思维导图，有利于学生把握知识之间的联系，完善知识结构。

对“运算律”单元知识点的梳理要做到全面准确，不仅要注重对不同运算律进行分析和比较，还要注重对运算律进行分类比较。笔者引导学生绘制“运算律”单元思维导图（如图7），帮助学生整体构建对运算律的认识。

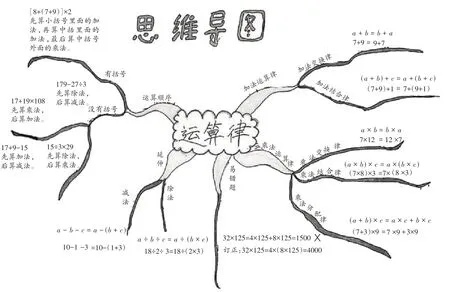
图7

《课程标准》指出，数学课程要培养的学生核心素养，主要包括以下三个方面：会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界。综上所述，核心素养视域下的单元整体教学，以教学内容的本质及其所体现的核心素养表现为统领，将具有内在一致性的知识进行整合。在单元整体教学中，教师设计单元主题，串联各知识点，整体建构单元知识体系，能帮助学生更好地感悟数学内容的本质、关注数学内容之间的关联，更有效地建立体现数学学科本质、对未来学习有支撑意义的结构化的数学知识体系。