汽轮机整圈自锁叶片强度与振动特性分析

陈 键，周 琴，张鲲羽，王景胜

（上海船舶设备研究所，上海 200031）

0 引言

汽轮机是将热能转换为机械能的动力设备。叶片作为核心零部件，借助叶根固定在转子的轮缘上，在汽轮机的运行中承担着将蒸汽的热能转化为机械能的重要任务。根据研究发现，因叶片损害导致的机组停机事故占所有事故中的一大半，所以为确保机组在运行时的安全性和可靠性，通常需要对汽轮发电机组叶片进行强度校核和振动特性计算[1]。

随着现代数字化仿真技术的发展，特别是全三维实体网格和非线性计算的进步，通过大型数值仿真平台能够实现了对叶片强度和振动频率的计算，给出数值解析值，避免了复杂难解的理论计算，有效降低了实验成本，优化叶片设计，加快叶片研发的过程，成为目前汽轮机设计过程中的重要一项。

整圈自锁叶片相较于自由叶片和成组叶片具有明显的优势：增加了叶片整体刚度，降低了共振的风险；同时提高了结构阻尼，降低了动应力；叶轮静应力较小，强度隐患低。但其设计难度也比后二者大大增加[2]。

本文通过建立某型汽轮机的整圈自锁叶片的三叶片-轮缘模型和单叶片模型，通过ANSYS Workbench仿真软件平台对叶片在工作转速下的等效应力强度与整圈振动特性进行仿真计算分析。

1 建立模型

图1为叶片围带三维模型及围带间的接触示意图，考虑到该叶片的长度较短，扭转量小，因此将围带间的接触距离设计为贴合状态，以确保有足够的接触面应力。

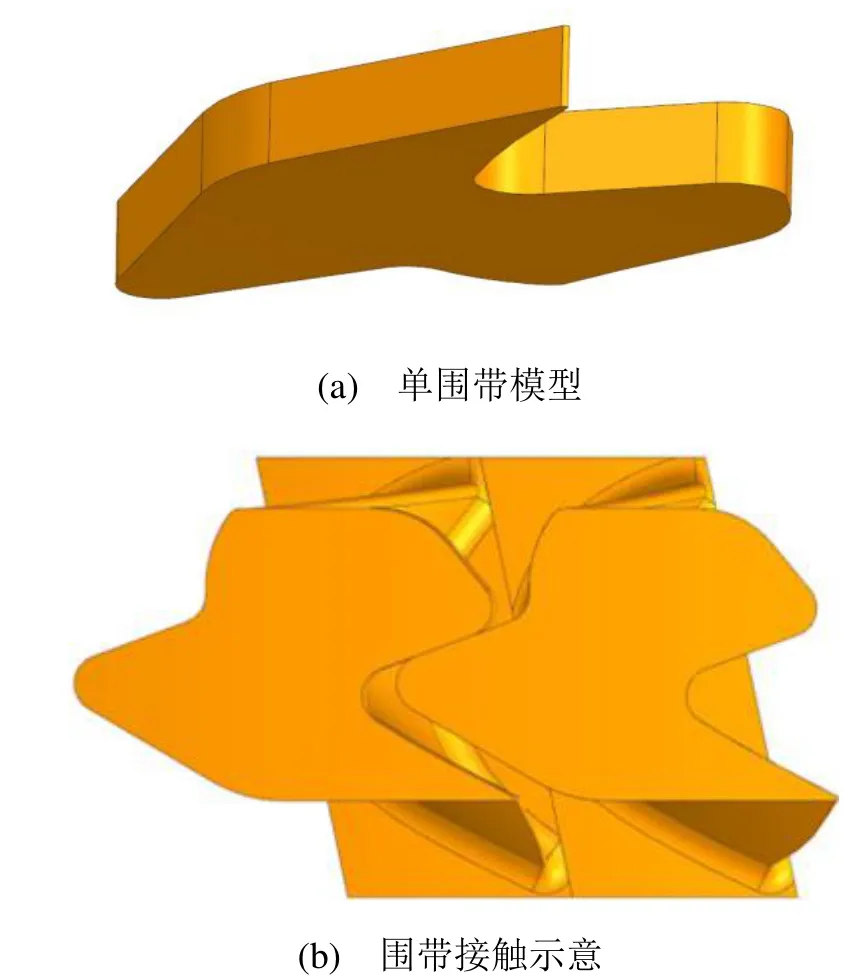
图1 围带三维模型

根据机组的实际情况，同时简化模型、减少计算时间，采用了3叶片成组的方式对其进行有限元强度计算分析，仅考核中间叶片的计算结果，具体模型见图2。叶片采用了枞树型叶根，安装方式采用了轴向安装。

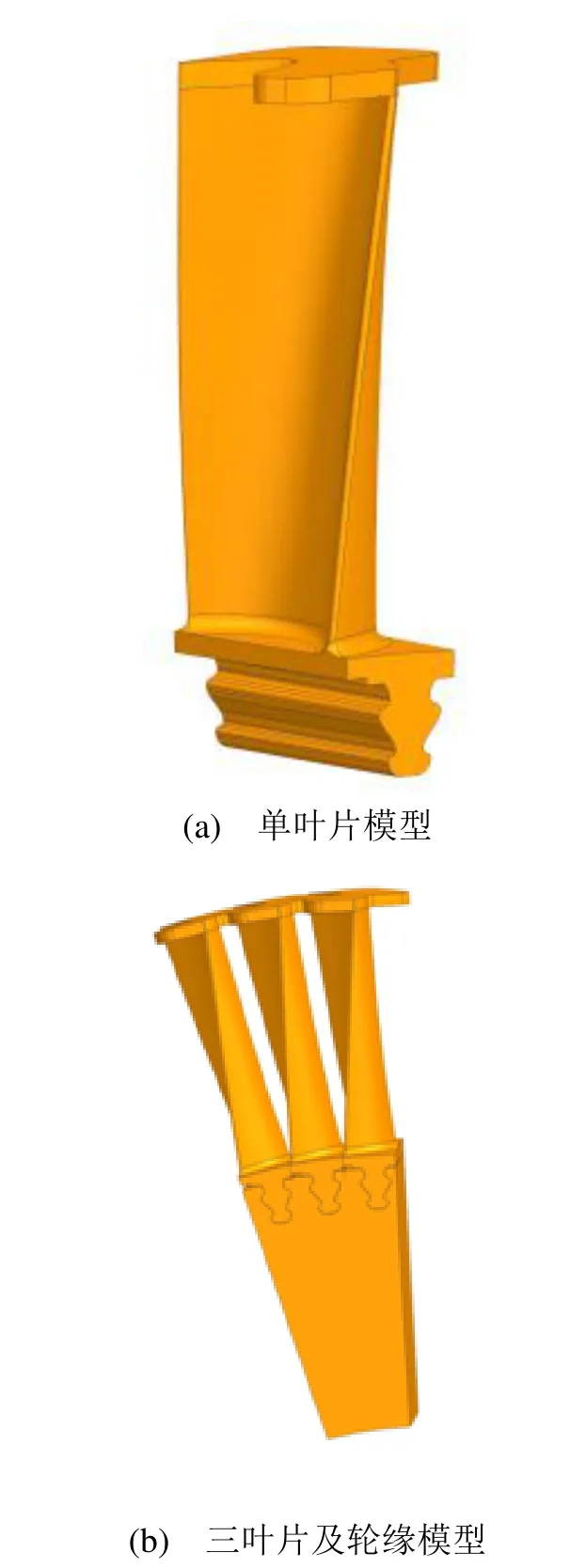
图2 三维模型

2 强度计算

2.1 强度计算模型

通过ANSA前处理软件对模型进行网格划分。除了围带与叶片、叶片与叶根的过渡区域选取了四面体和四棱锥网格划分，模型的其他区域选择了8节点的六面体单元进行网格划分，为获得精确的计算结果，对叶片叶根和轮毂的网格进行细化处理，保证叶根接触面的网格质量，同时对叶根倒圆处网格进行加密并保证网格为高质量六面体网格。模型的网格划分见图3和图4。

图3 三叶片-轮缘模型

图4 局部网格划分

2.2 材料设置及边界条件

叶片及转子材料特性见表1。

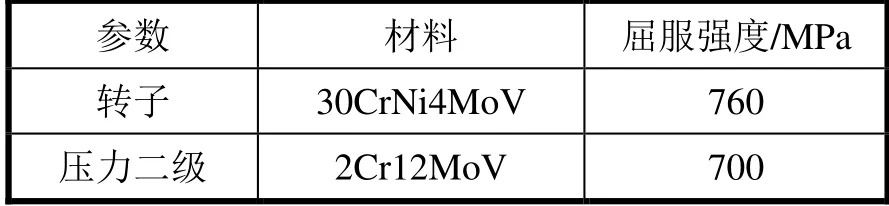
表1 叶片及转子材料特性表

汽轮机在工作时，叶片将受到离心力、重力和轴向的汽流力、汽流激振力等多种影响。由于气动力和重力对旋转机械强度的影响非常小，只需要考虑高速转动的离心力载荷[3]。同时，叶片整圈安装在轮缘上，且做匀速圆周运动，各个叶片之间锁死贴合。综上所述，其计算模型的边界条件可以简化为：

1）扇形轮缘两侧施加周向位移约束。

2）第1个叶片与第3个叶片的两侧施加周向位移约束，第2个叶片施加恒定转速。

3）叶片与叶片之间有接触的地方均设置为自动接触对，摩擦系数0.2。

4）轮缘与叶片之间所有可能在受力过程中发生接触的地方均设置为自动接触对，摩擦系数0.2。5）扇形轮缘下表面所有节点施加固定约束。通过考核中间叶片的应力强度，对该叶片的强度进行校核。

2.3 强度计算结果

通过工作转速下对叶片-轮缘进行三维有限元分析，获得了该转速下叶片及轮缘的变形和等效应力分布情况，见图5，叶片在高速离心力的作用下，叶根下倒圆角处有较大的应力集中。

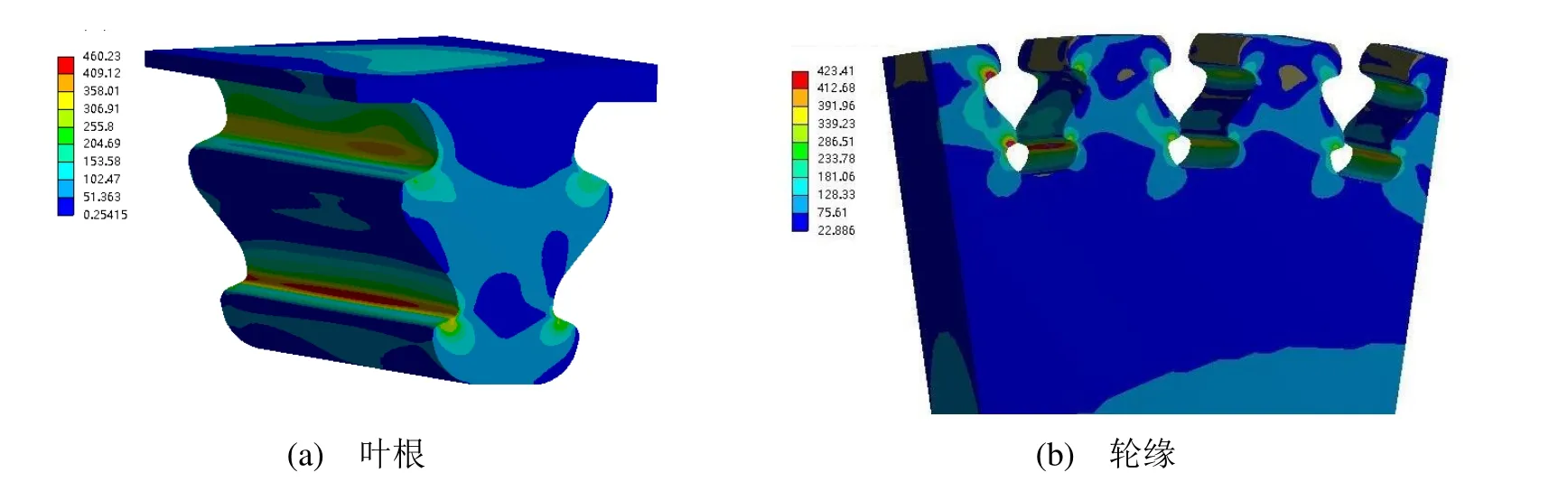
图5 叶根及叶轮应力分布云图

由叶片强度校核计算结果可知，叶根的最大等效应力强度为460.23 MPa，轮缘的最大等效应力强度为423.41 MPa。在工作转速下，叶片及叶轮的最大应力均低于材料的屈服强度，满足工程应用要求。

3 振动特性计算

3.1 锁紧转速分析

通过采用第3节中的计算模型，进一步对每间隔200 r/min转速进行多转速下的仿真计算。根据实际工程设计经验，当围带接触面的最大接触压力接近10 MPa时，可以认为相邻叶片被锁紧，叶片-轮缘模型整圈振动。通过查看仿真计算结果得到，在某一转速下围带间的接触面应力分布情况，见图6。由图6可知，在该转速下，相邻围带之间的接触应力最大为9.9 MPa。即该转速为叶片围带的锁紧转速。

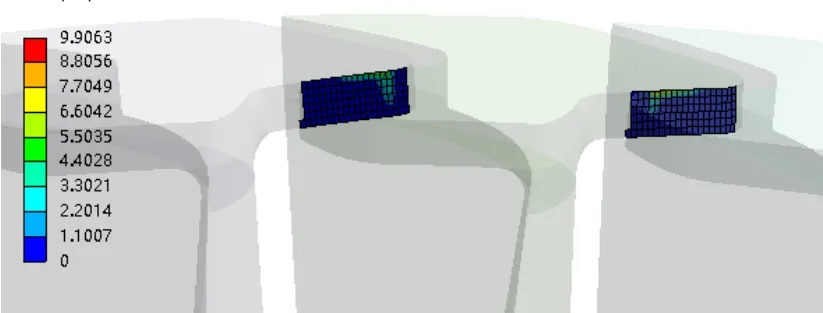
图6 2 400 r/min 下围带接触面应力分布

3.2 振动特性计算模型

该计算采用了整圈1/66的单叶片-轮缘模型。叶片及轮缘的网格划分方式与第2.1节相同。在超过锁紧转速后，围带接触面已锁紧，为模拟锁紧转速下相邻叶片围带接触面间的相互接触状况，将围带接触面区域中心位置处的4个节点进行合并。为此，对围带进行切块，并对切面进行设置周期循环边界条件，网格划分结果见图7和图8。

图7 单叶片-轮缘模型

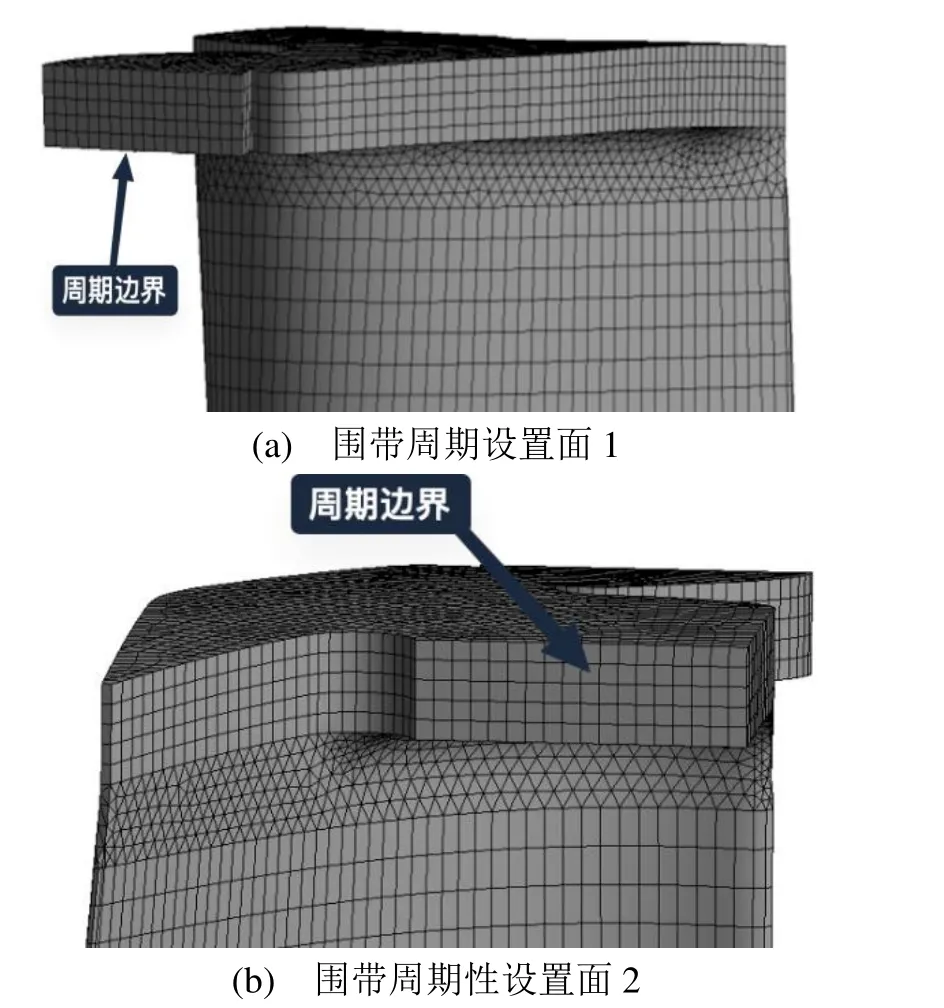
图8 单叶片-轮缘周期对称面设置

3.3 材料设置及边界条件

叶片及轮缘的材料参数设置与第2.2节相同。

对单叶片-轮缘模型进行周期性边界条件设置：

1）围带切块部分的周期性边界网格节点一一对应，设置周期循环对称。

2）轮缘两侧的周期性边界网格节点一一对应，设置周期循环对称。

3）考虑到工作转速下，叶根与轮缘的接触面已贴合紧密，因此将叶根齿面与轮缘齿接触面上的网格进行了绑定约束。

4）对叶片和轮缘施加恒定转速。

在ANSYS Workbench中，通过使用预应力模块，通过Symmetry插入周期性循环对称边界Pre-Meshed Cyclic Region，设置好围带与轮缘切面的周期性边界条件，输入循环对称数量为66，形成周期循环对称的整圈模型。

3.4 整圈振动计算结果

图9为仿真计算结果的部分振型图。

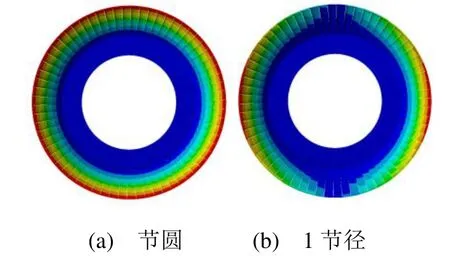
图9 1 阶振型图

由黄文虎教授提出的“三重点”调频理论[4]是判断系统发生共振的一种有效的方法，其定义为

式中：fm为节径数为m时叶片频率；m为节径数；K为激振力谐波数；ω为激振力的基频。

通过对叶片施加不同转速，得到不同转速下模型整圈振动的动频值，绘制坎贝尔图，见图10～图13。

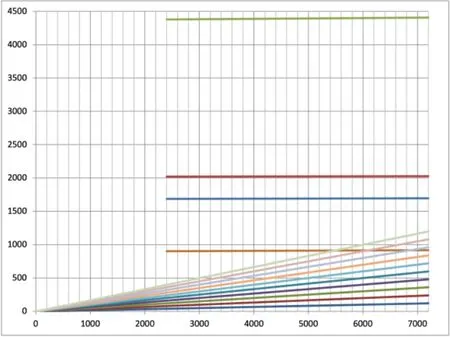
图10 叶片-叶缘模型节圆振动（前4 阶）坎贝尔图

图10是节圆振动的坎贝尔图，绘制了整圈叶片的节圆和前3阶节径振动。节圆振动在工作转速时与激振力没有“三重点”，所以不会产生共振。1阶节圆振动的频率为917.74 Hz，与8阶激振力960 Hz的避开率为4.4%。一般认为节圆振动（0节径数的振动）可以不调频[5]。

同时，从图11～图13可以看出，前3节径的10阶振动坎贝尔图中不存在与节径数相同的激励力阶次交点，轮系振动频率具有良好的避开率，在工作转速范围内没有出现“三重点”。

图11 叶片-叶缘模型第1 阶节径振动（前10 阶）坎贝尔图

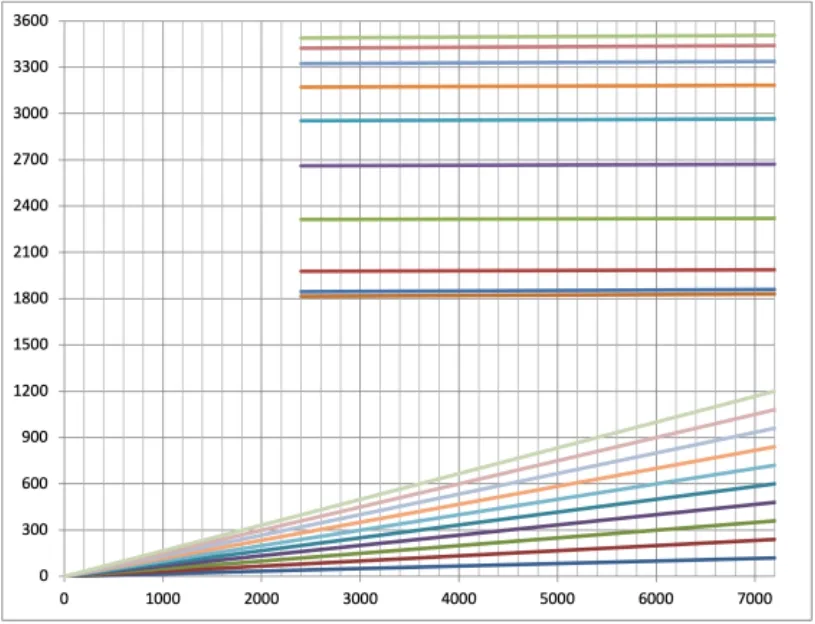
图12 叶片-叶缘模型第2 阶节径振动（前10 阶）坎贝尔图

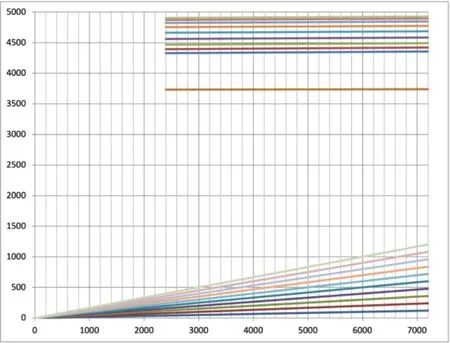
图13 叶片-叶缘模型第3 阶节径振动（前10 阶）坎贝尔图

4 结论

本文采用了数值仿真的方法，对三维叶片模型的应力强度以及整圈振动特性进行计算，得到了叶片及其轮缘的应力强度分布以及整圈动频值、振型。通过仿真计算结果可知，在工作转速下，该叶片的最大应力强度均小于材料屈服强度，满足工程应用的要求。通过绘制相关坎贝尔图可知，轮系振动频率不存在产生共振的“三重点”，具有良好的避开率。综上，该叶片设计满足汽轮机组工作运行的安全性要求。同时，文中的仿真方法及计算结果可为后续的叶片结构设计提供了数值指导。