适应火工装置冲击环境的铝蜂窝缓冲特性研究
史文辉,岳 帅,刘 洲,肖余之,杜忠华,刘 志,高光发
(1.南京理工大学 机械工程学院,南京 210094;2.上海宇航系统工程研究所,上海 201109; 3.上海航天技术研究院,上海 201109)
火工装置是指装有火药或炸药,受外界能量刺激后产生燃烧和爆炸,用以引燃火药或引爆炸药作机械功或产生特种效应的一次性使用装置的总称,主要由发火元件、装药和功能结构组成。具有体积小、比能量大、使用简单、作用速度快、功能可靠和性能可设计等优点,在航天飞行器中得到了广泛的应用[1-2]。火工装置在工作时会对邻近结构产生剧烈的局部机械瞬态响应[3-4],火工冲击主要为高频瞬态冲击,主要特点是高量级、时间短,传播形式为应力波[5-6]。这种冲击载荷会使航天器结构特别是电子系统和光学元器件损伤或失效[7],严重时可能导致整个航天任务的失败[8]。1999年美国颁布了NASA-STD-7003爆炸冲击试验规范,并于2011年升级为NASA-STD-7003A,系统地介绍了航天器爆炸冲击试验规范,阐述了爆炸冲击试验环境的特点、环境预示方法以及爆炸冲击的试验模拟技术等。国内也建立了GJB150.18A-2009冲击试验标准,规定了军用装备冲击试验的相关要求。
为了改善卫星发射过程的力学环境,降低卫星设计成本,往往需要设计主动或被动减振装置[9]。目前降低火工冲击载荷的方法主要有以下几种:① 调整装药量或燃气释放速度,减小快速点火和燃烧产生的冲击;② 在装置内部设计缓冲机构,用塑性材料或弹性材料吸收能量;③ 增加负载释放的时间,来降低负载突然释放产生的冲击;④ 低冲击分离装置的研制[10-11]。铝蜂窝具有相对密度低、质量轻、比刚度比强度高、缓冲吸能性能好、耐腐蚀耐老化和制造工艺成熟等特点[12-13],常作为一种一次性缓冲器材及防撞结构应用在航天器上吸收冲击能量[14]。
目前国内外学者对于火工冲击载荷的研究主要集中于加速度冲击响应谱不同频段的冲击响应特征[15-16],还有学者分析了预紧力、药量和不同缓冲材料等主要因素对爆炸螺栓冲击响应谱的影响[17-18]。Shi等[19-20]研究了有无铝蜂窝缓冲器和卫星温度变化对火工装置的影响。上述大部分研究主要侧重针对火工装置的冲击响应谱特性分析与冲击减缓,缺乏考虑火工装置动态作用过程中与缓冲结构相互耦合下的动力学特性研究,并鲜有对火工发射装置与缓冲力、缓冲行程等参数之间的相互掣肘关系的分析。鉴于此,本文在一种新型空间火工装置发射缓冲结构基础上建立了基于变化载荷与铝蜂窝规格的火工装置发射动力学模型,并对其进行了多工况发射条件下的参数分析与试验验证,重点研究了不同火工载荷和不同规格铝蜂窝对空间火工发射装置后坐力及发射性能的影响。
1 空间火工发射装置缓冲吸能结构
空间火工装置为绳网发射提供能量,点火器点燃火药产生大量高温高压气体,推动牵引体沿着发射筒运动。通过调整火药药量可以控制牵引体的发射速度,满足不同的任务需求。然而,在发射过程中,火药气体除了提供牵引体前进的能量,还产生后坐力。如果后坐力过大,会对发射装置和卫星平台产生重大影响,威胁任务的顺利完成。因此,需要在发射装置和卫星平台之间安装缓冲装置,以吸收多余的能量,保证发射过程的安全。
本文设计了一种新型空间火工装置发射缓冲吸能结构,如图1所示。零件主要参数如表1所示。在该结构中,火药置于发射腔体和发射腔盖之间。点火器通过螺纹与发射腔盖连接,上垫板和下垫板之间放置铝蜂窝,底板固定在发射架上。上垫板和下垫板上均布有六个通孔,套筒穿过上垫板和铝蜂窝通过螺纹固定在下垫板上,保证铝蜂窝沿其高度方向被压溃,降低其他因素的影响。
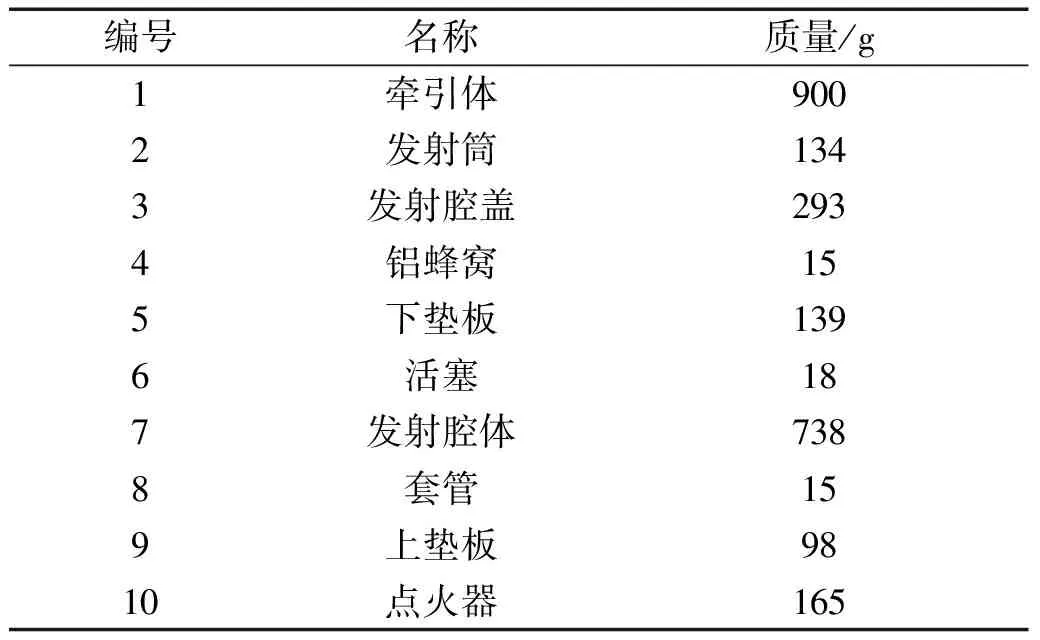
表1 零件名称表
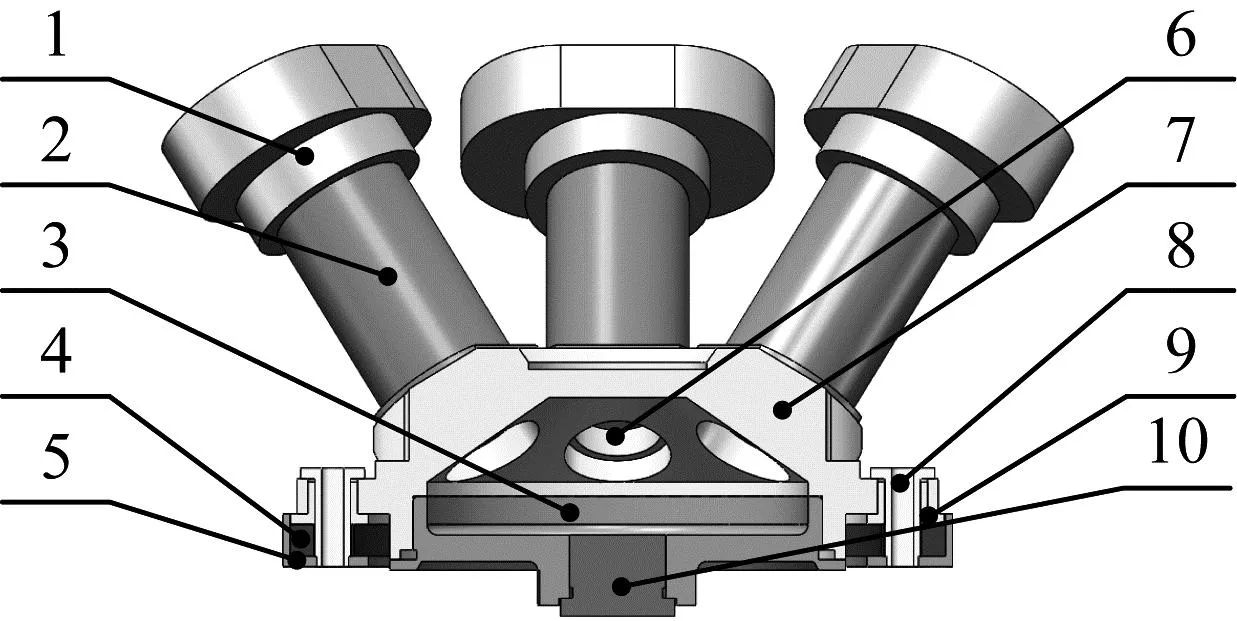
图1 缓冲结构
当点火器收到点火信号时,点火器开始工作,先引燃点火器附近的火药,随着火药继续燃烧,其余火药被点燃。火药燃烧产生的大量高温高压气体作用在发射腔体、发射腔盖和活塞上。作用在活塞上的气体会推动牵引体使其达到一定的速度,作用在发射腔体和发射腔盖上的气体形成了后坐力。随着火药的持续燃烧,当上垫板向下的作用力大于铝蜂窝的平面压溃力时,铝蜂窝开始被压溃,使后坐力一直保持在一个稳定的范围内,保证发射装置和平台的安全可靠。
2 内弹道模型
2.1 密爆试验
密爆试验通常用于研究火药在定容条件下的燃烧过程和火药燃烧规律。从密爆试验中可以得到火药燃烧的峰值压力和峰值时间,进而可以得到火药的火药力和燃速系数这两个关键参数,并将其作为内弹道模型的输入条件来获得更加准确的膛压曲线。
在密闭爆发器中,若不计热量损失,根据热力学第一定律有[21]
dQ=dE+PdW
(1)
式中:dQ为进入工作容积内的热量变化量;dE为气体内能的变化量;PdW为气体膨胀做功能量的变化量。
在定容条件下,如果火药固体体积很小,则气体膨胀做功PdW可以忽略,即火药燃烧产生的所有热能全部转化为气体的内能,则有:
dQ=dE,Q=E
(2)
在火药燃烧过程中,气体质量ωg=ωψ不断增大,因此与之对应的热量也不断增大
Q=QWωg
(3)
式中:ω为装药质量;ψ为火药燃去的质量分数;ωg为燃烧过程中转变为气相的装药质量;QW为火药的爆热。
定容条件下,气体内能为
E=ωgcvT
(4)
引入比热比k=cp/cv,并考虑迈耶方程
cp-cv=R
(5)
E=ωgRT/(k-1)
(6)
P=ωgRT/(W-αωg)
(7)
E=PW/θ
(8)
式中:cp为定压比热;cv为定容比热;T为温度;R为气体常数;α为余容,其值为1×10-3m3/kg;P为膛压;θ为绝热系数,θ=k-1。
联立式(3)和式(8),可得:
PW=θQWωg=θcVT1ωψ=RT1ωψ
(9)
式中:QW=cvT1;cv=R/θ。
P=RT1ωψ/W=fωψ/W
(10)
式中,f=RT1为火药力。
当火药已燃质量比为ψ,压力Pψ=P,气体体积Wψ=W,则:
Pψ=fωψ/Wψ
(11)
Wψ=W0-ω(1-ψ)/δ-αωψ
(12)
式中:Wψ为药室自由容积;W0为药室初始容积。
当火药燃烧开始前有
Wψ=W0-ω/δ
(13)
当火药结束燃烧时有
Wψ=W0-αω
(14)
根据式(11)可得,定容条件下的峰值膛压Pmm出现在火药结束燃烧瞬间,此时ψ=1,则有:
(15)
令装填密度Δ=ω/W0,有:
(16)
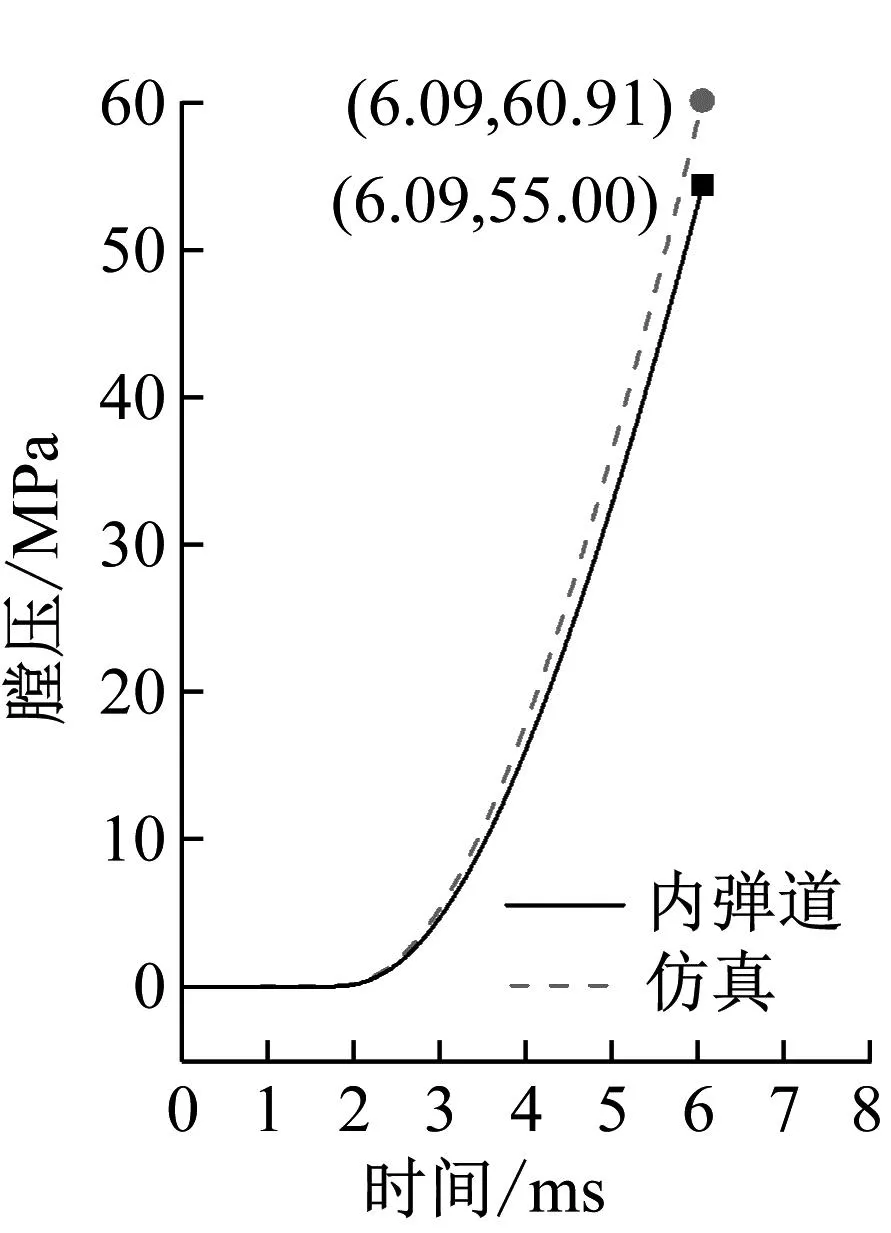
密爆试验在室温下进行,密闭爆发器的容积为530 mL,火药种类为HY-5,火药质量为7.3 g。为了降低随机性和误差,共进行了三次试验。通过定容内弹道模型匹配得到了三次试验的火药力和燃速系数,试验和仿真结果如图2所示。从膛压曲线可以看出,仿真与试验结果吻合较好。在定容条件下,初始点火阶段,随着火药的燃烧膛压逐渐升高。当火药气体充满密闭爆发器时,膛压保持稳定,直到火药燃烧完成。
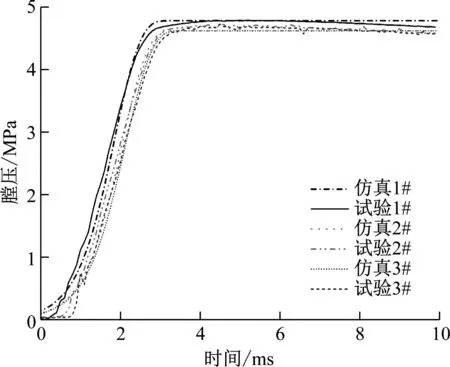
图2 密爆试验与仿真结果
通过密爆试验和定容内弹道模型求解得到的主要参数如表2所示。相比于试验,仿真峰值压力最大误差为2.12%,证明了定容内弹道模型的准确性。因此可以得到火药的平均火药力为0.293 MJ/kg,平均燃速系数为2.93×10-5mm/(MPa·s)。

表2 试验与仿真结果
2.2 内弹道求解
为了得到发射过程中产生的后坐力,需要对牵引体发射内弹道进行求解。本文中6个发射筒共用一个发射腔体,因此需要将多个发射筒和牵引体等效为一个。根据等效原理[22],等效后的发射筒横截面积为6个发射筒横截面积之和,牵引体质量为6个牵引体质量之和。每个牵引体通过两个剪切销钉与发射筒固定,铜销的直径为2.6 mm,材料为黄铜,其剪切强度为300 MPa,则单个剪切销钉的剪切力为1 600 N,将其转化为牵引体的启动压力P0=3.52 MPa。根据经典内弹道理论建立内弹道模型如下[23]
(17)
式中:ψ为火药已燃质量比;χ,λ,μ为火药形状特征量,仅取决于火药形状与尺寸;z为火药相对厚度;t为时间;u1为燃速系数;e1为药粒原始厚度的一半;P为气体压力;n为燃烧指数;φ为次要功系数;m为牵引体质量;v为牵引体速度;S为发射筒横截面积;l为牵引体位移;lψ为药室自由容积缩颈长;f为火药力;ω为火药质量;θ为绝热系数。
通过对上述内弹道模型进行求解,得到内弹道曲线如图3所示。当膛压小于启动膛压力时(A-C),牵引体静止不动。当膛压大于启动膛压后(C-Pm),牵引体开始运动,此阶段火药气体产生速率的影响大于牵引体运动后空间体积增长的影响,膛压曲线将持续上升。当这两种影响达到平衡时,膛压达到最大值。随着牵引体速度的不断增加,牵引体运动后空间体积上升的影响超过了气体生成速率的影响,膛压开始下降(Pm-D)。当火药完全燃烧时,膛压随着牵引体速度的增加而减小。
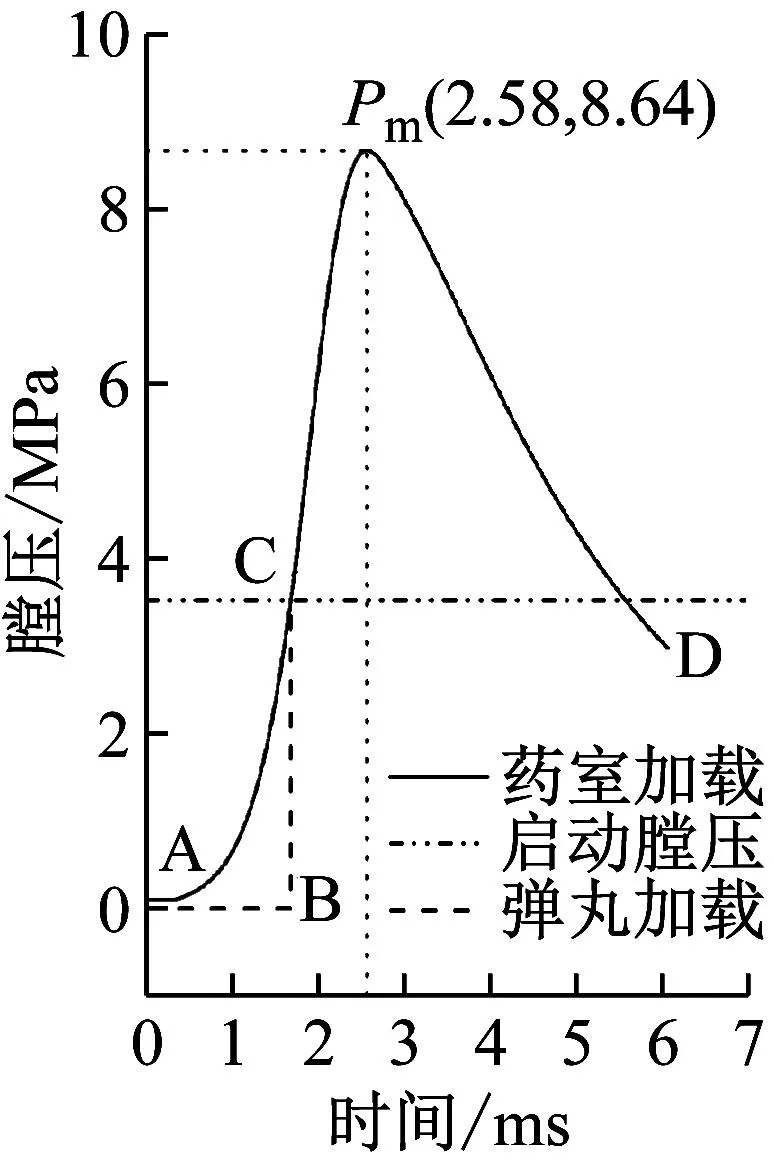
图3 内弹道曲线
如上所述,单个牵引体在发射前用两个剪切销固定,只有当膛压超过剪切销的剪切强度(即启动膛压)时,牵引体才开始运动。因此,加载在牵引体上的膛压分为A-B-C阶段和C-D阶段。由图3可知,牵引体离开发射筒的位移为55 mm,速度为22.21 m/s,位移和速度在约前2 ms左右保持为零,此阶段对应膛压曲线的A-B-C阶段,此时膛压未达到启动膛压,随后牵引体开始运动直到离开发射筒。
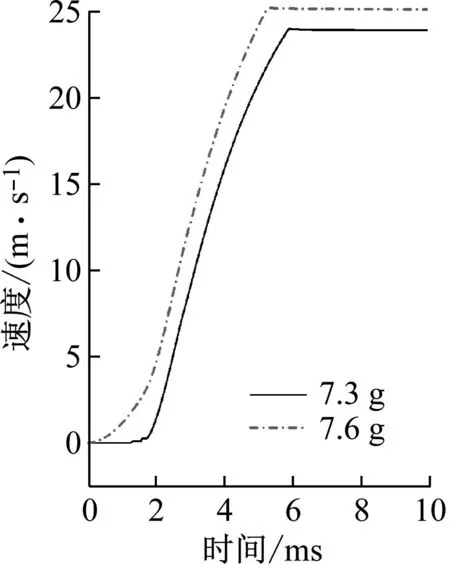
对于火工装置来说,主要影响因素为火药的性能和发射器,体现在火药的火药力、燃素系数和启动膛压这三个关键参数,而这三个参数的影响可以通过火药药量来控制。为了满足发射速度精度要求,将药量定为7.3 g和7.6 g两种情况,得到如图4所示的内弹道曲线。可以看出药量增加,峰值膛压增大,峰值时间提前,牵引体的速度增大。
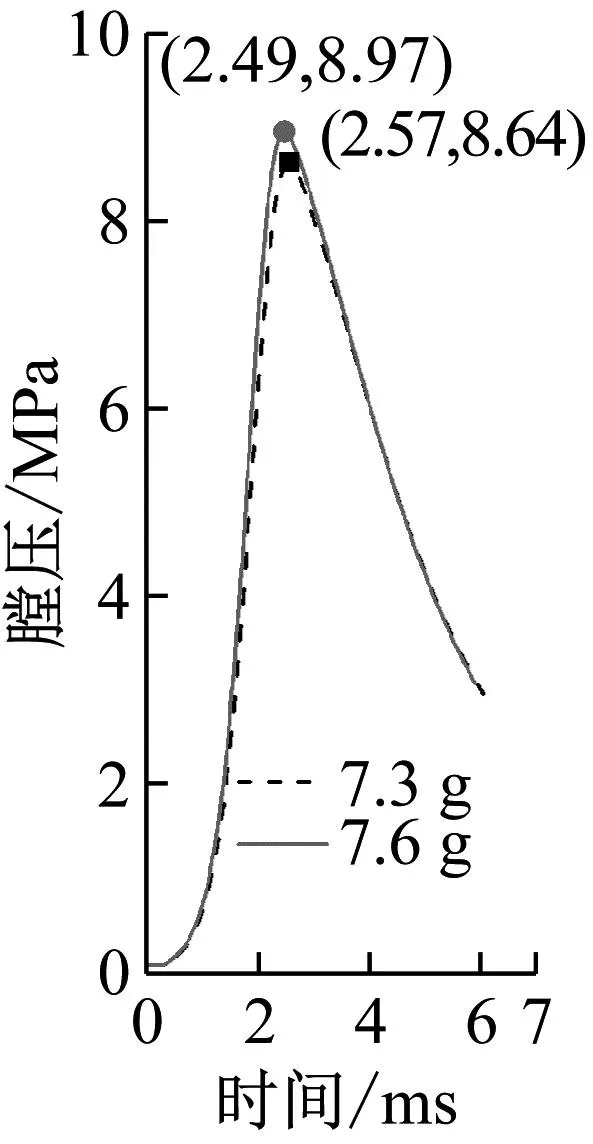
图4 不同药量内弹道曲线
3 铝蜂窝准静态性能研究
3.1 铝蜂窝准静态压溃试验
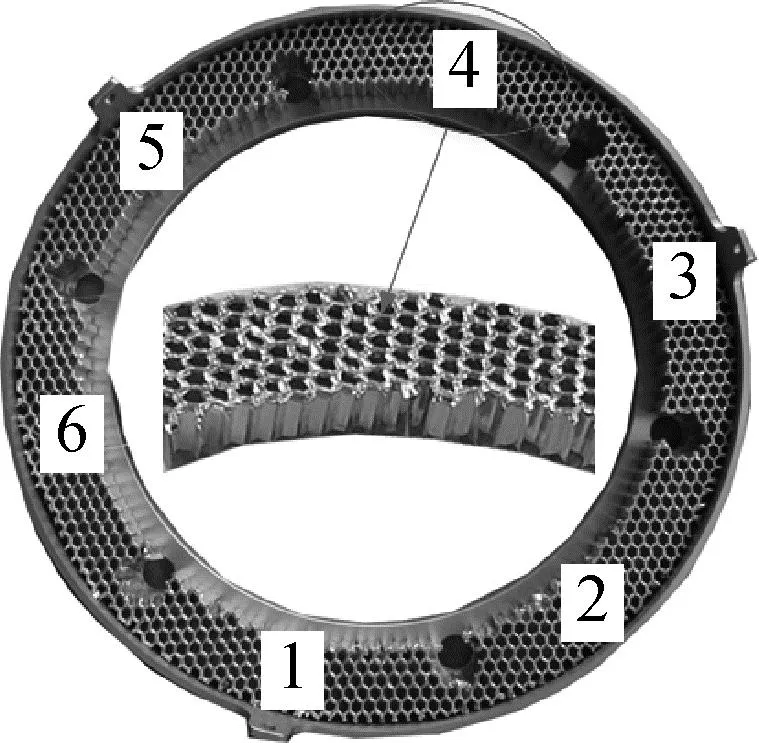
根据卫星发射平台设计要求,当发射后坐力小于21 kN时,不会对卫星发射平台产生影响,为此采用铝蜂窝对发射后坐力进行缓冲吸能。如图5所示,铝蜂窝试件为圆环状,横截面积为8 867 mm2。因此平面压溃强度为2.37 MPa。根据HB5443—1990《夹层结构用耐久铝蜂窝芯材规范》,可确定铝蜂窝材料为3003,公称密度为105 kg/m3,胞元边长为2 mm,铝箔厚度为0.05 mm。
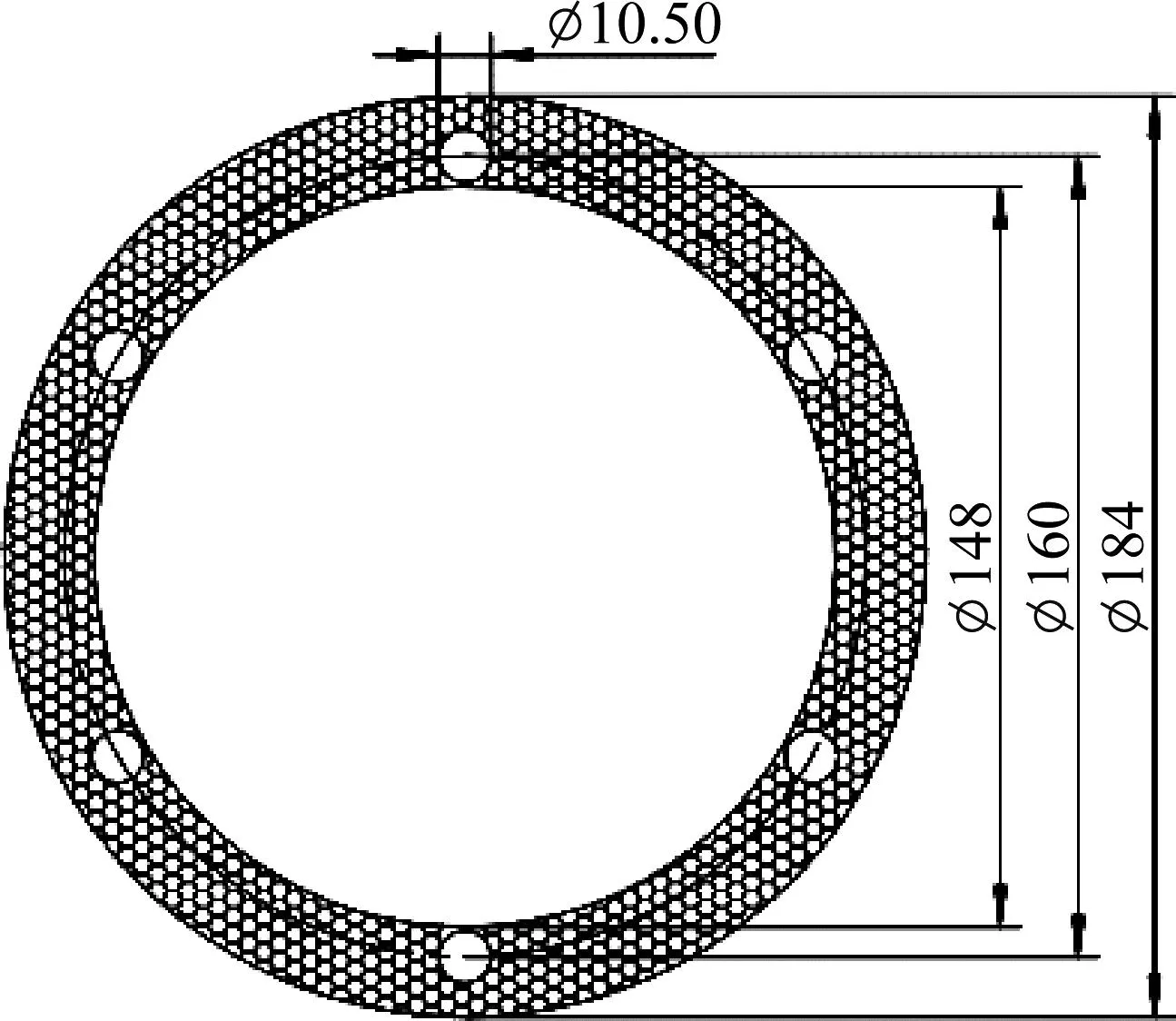
图5 铝蜂窝试件外形
利用ETM系列万能试验机对铝蜂窝进行准静态压溃试验。加载速度为2 mm/min,试验得到的载荷-位移曲线可以分为四个部分:弹性阶段、渐进屈曲阶段、稳态压溃阶段和密实阶段。其中稳态压溃阶段为铝蜂窝主要能量吸收阶段,在该阶段随着位移的增加,荷载基本保持不变[24]。
为了使铝蜂窝在压溃吸能过程中作用力保持稳定,需要消除渐进屈曲阶段,根据多次准静态试验结果可得铝蜂窝试件的渐进屈曲阶段基本上在1~3 mm,当位移超过3 mm,铝蜂窝的压溃力便呈现出比较平稳的状态,因此确定预压溃高度为3 mm。当铝蜂窝再次被压溃时,载荷-位移曲线将从弹性阶段直接转移到稳态压溃阶段,保证了吸能效果的稳定性。
根据缓冲机构的设计参数可得,铝蜂窝试件的外径为184 mm,高度只能为9 mm,上述计算是基于铝蜂窝的胞元全部完整,而在实际加工过程中由于铝蜂窝为圆环状,无法保证其有效胞元的个数,因此通过对铝蜂窝内径的改变适当增加有效胞元个数,控制铝蜂窝的平面压缩强度。为了保证发射速度和后坐力的要求,设计了内径为146 mm、147 mm和148 mm三种尺寸的铝蜂窝,其预压溃载荷-位移曲线如图6所示。可以发现,压溃力在位移大于2.5 mm之后趋于稳定,则选择位移在2.5~3.5 mm的平均压溃力作为铝蜂窝的稳态压溃力,如表3所示,随着试件内径的减小,其有效胞元个数增加,稳态压溃力增大。
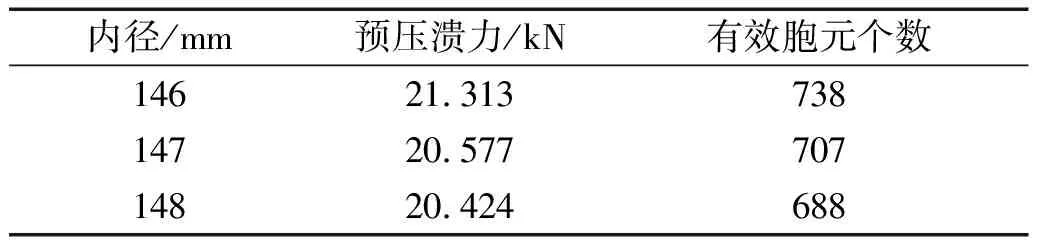
表3 预压溃试验结果
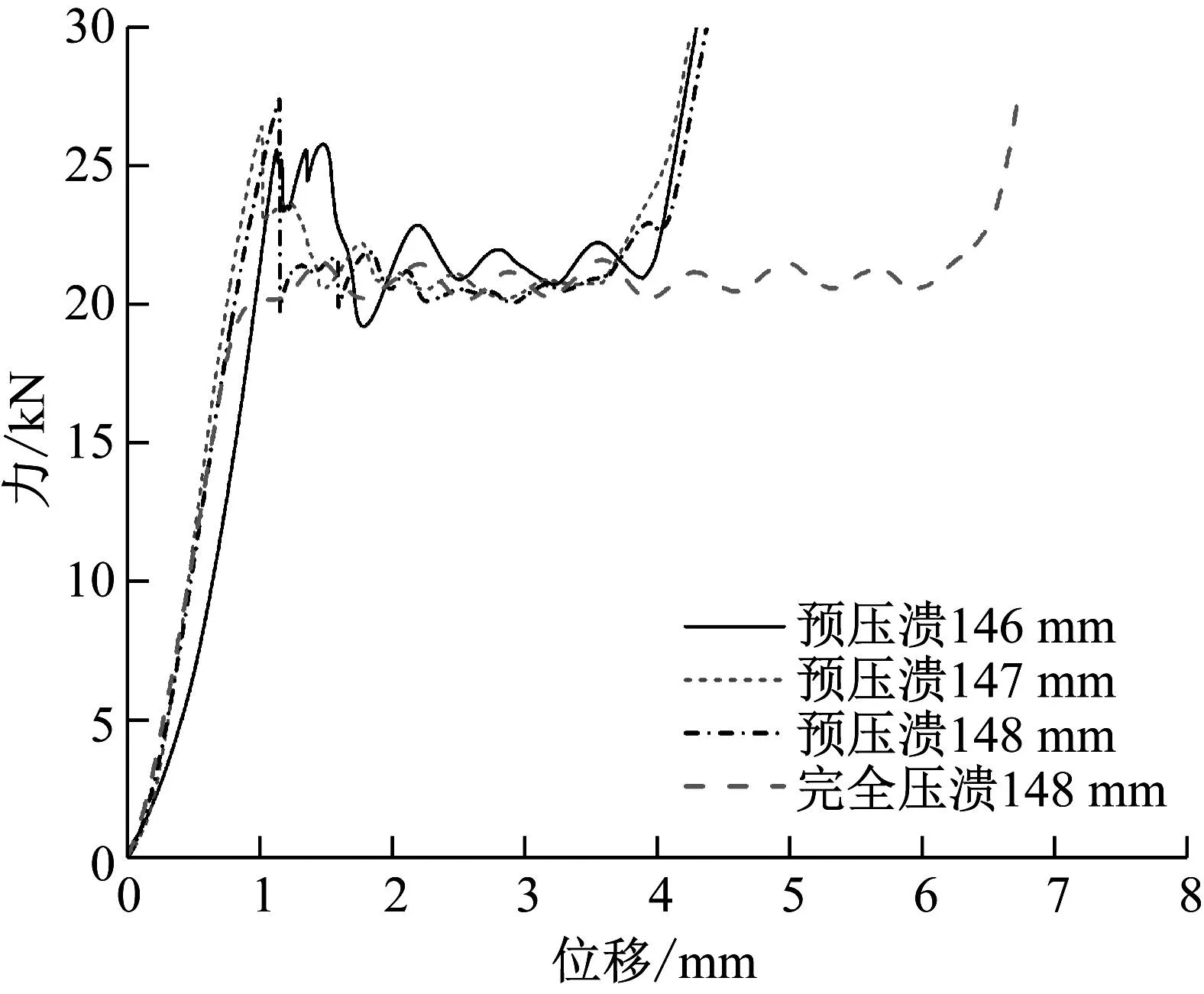
图6 准静态试验
同时为了研究铝蜂窝在预压溃前后的性能变化,对内径为148 mm的铝蜂窝试件进行了预压溃后的完全压溃试验,其载荷-位移曲线见图6。取完全压溃曲线位移在2.5~5.5 mm的平均作用力为稳态压溃力,其值20.782 kN。由于铝蜂窝的压溃力曲线存在一定的波动,完全压溃前后作用力相差358 N,占完全压溃稳态压溃力的1.7%,因此可以认为铝蜂窝在预压溃后性能稳定,对降低发射后坐力影响较小。
3.2 铝蜂窝准静态压溃仿真研究
为了模拟铝蜂窝的准静态压溃过程,采用ABAQUS中的塑性可压碎泡沫模型,该模型可以用于分析作为能量耗散结构的可压溃多孔结构和泡沫材料在压溃变形过程中由于胞壁屈曲而引起的能力增强。在此基础上存在两种强化模型:体积硬化模型和各向同性硬化模型。各向同性硬化模型假定拉伸和压溃的对称行为。屈服面演化受等效塑性应变控制,该应变由体积应变和偏移塑性应变所决定。因此,本文采用各向同性硬化模型[25]。
各向同性硬化模型是针对泡沫金属而建立的,该模型假定拉伸和压溃的行为相似。屈服面是p-q应力平面原点为中心的椭圆,屈服面以自相似的方式演化,并且由塑性应变控制。屈服面形状公式如下
(18)
式中:p为静水压力;q为米塞斯应力;B为屈服椭圆的q轴长度;α为屈服椭圆的形状因子。
屈服面在p-q应力平面中是一个椭圆,如图7所示。图7中:pc为材料静水压缩屈服强度;σc为单轴压缩屈服应力的绝对值。屈服椭圆的形状因子α为
(19)
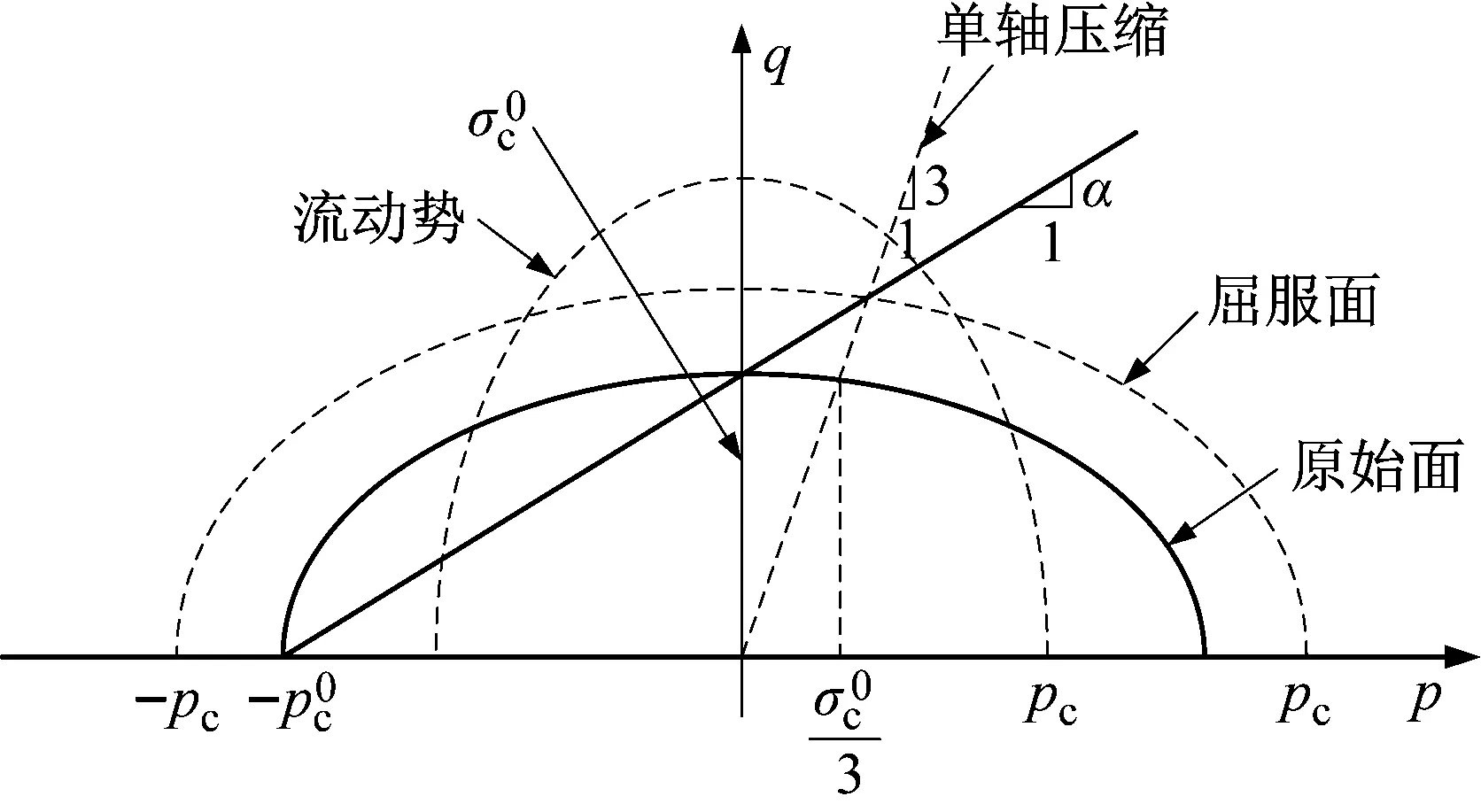
图7 各向同性可压碎泡沫模型在子午线平面上的屈服面和流动势
式中,kσ为压缩屈服应力比。
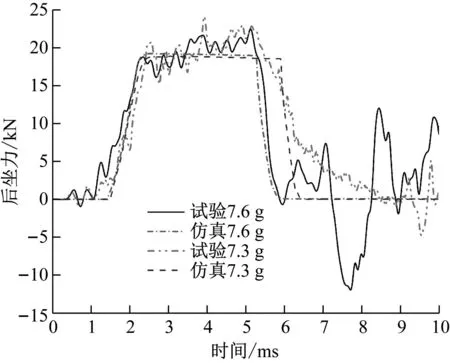
通过式(19)可以发现,压缩屈服应力比kσ必须满足0≤kσ<3,由于大多数泡沫材料的应力-应变曲面没有明显的屈服点,但都有一个明显的平台应力阶段,在该阶段中屈服应力几乎恒定不变,因此可以使用单轴压缩试验和静水试验的应力-应变曲线的平台应力来代替初始屈服应力计算压缩屈服应力比。
各向同性可压碎泡沫模型的流动势为
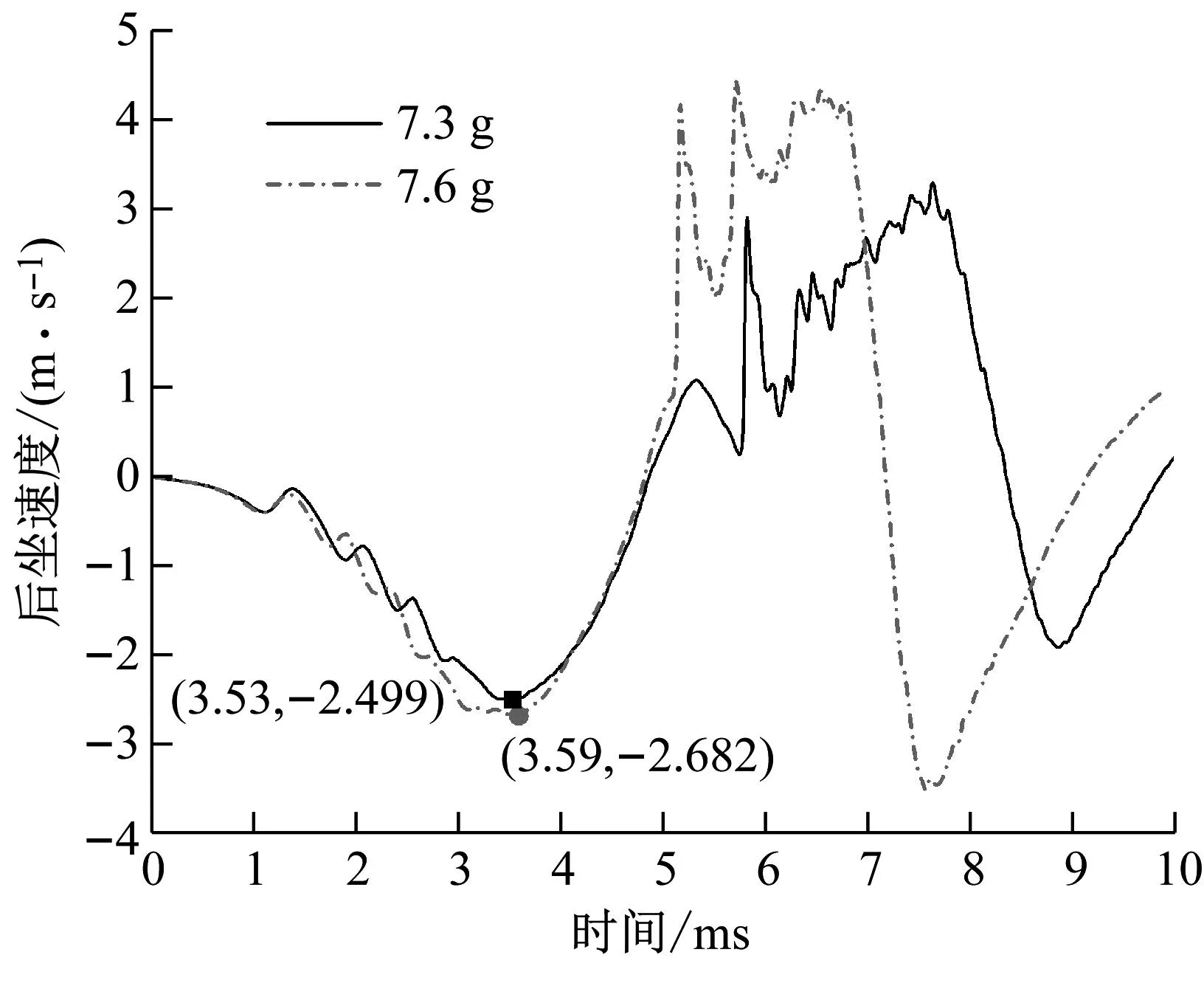
(20)
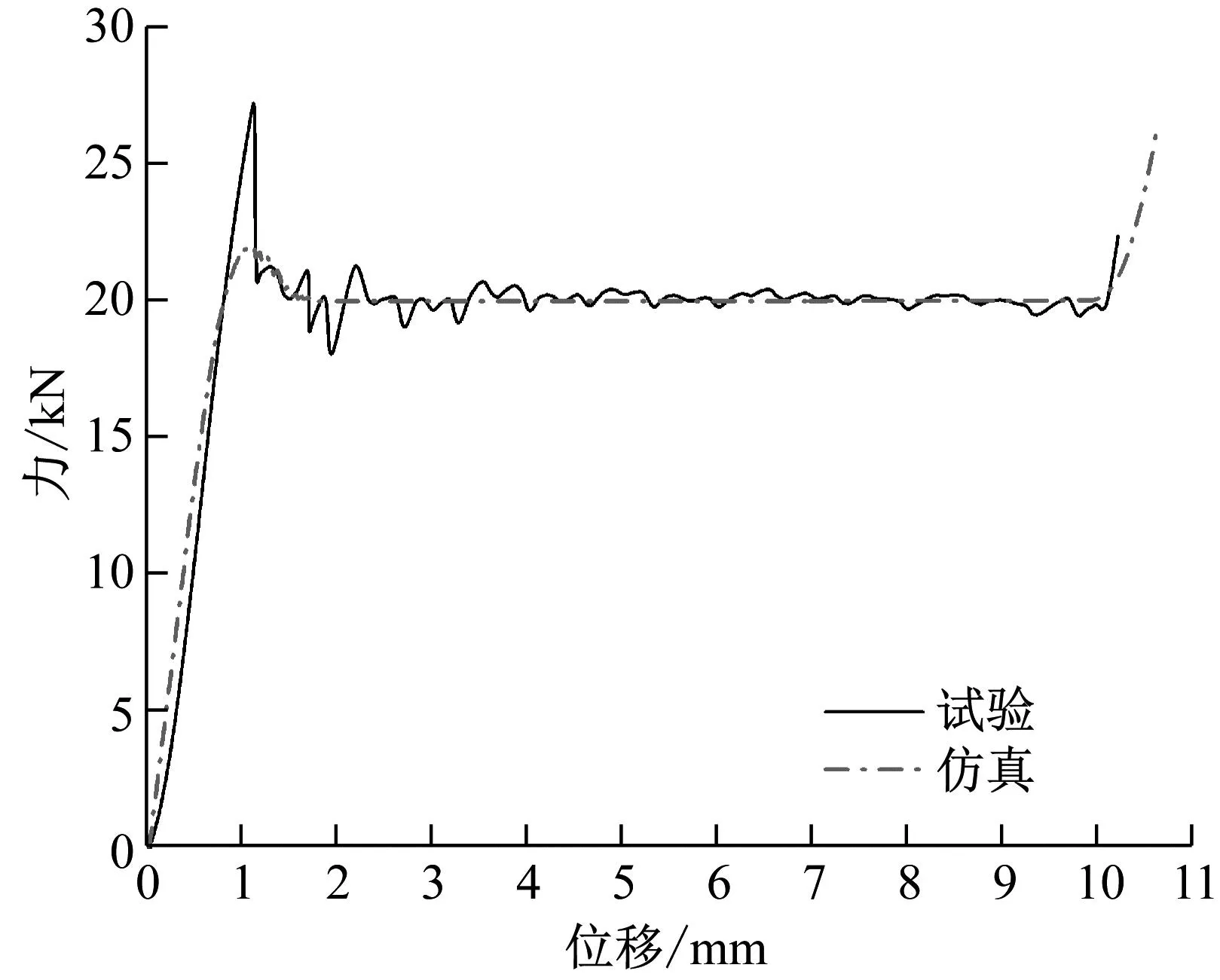
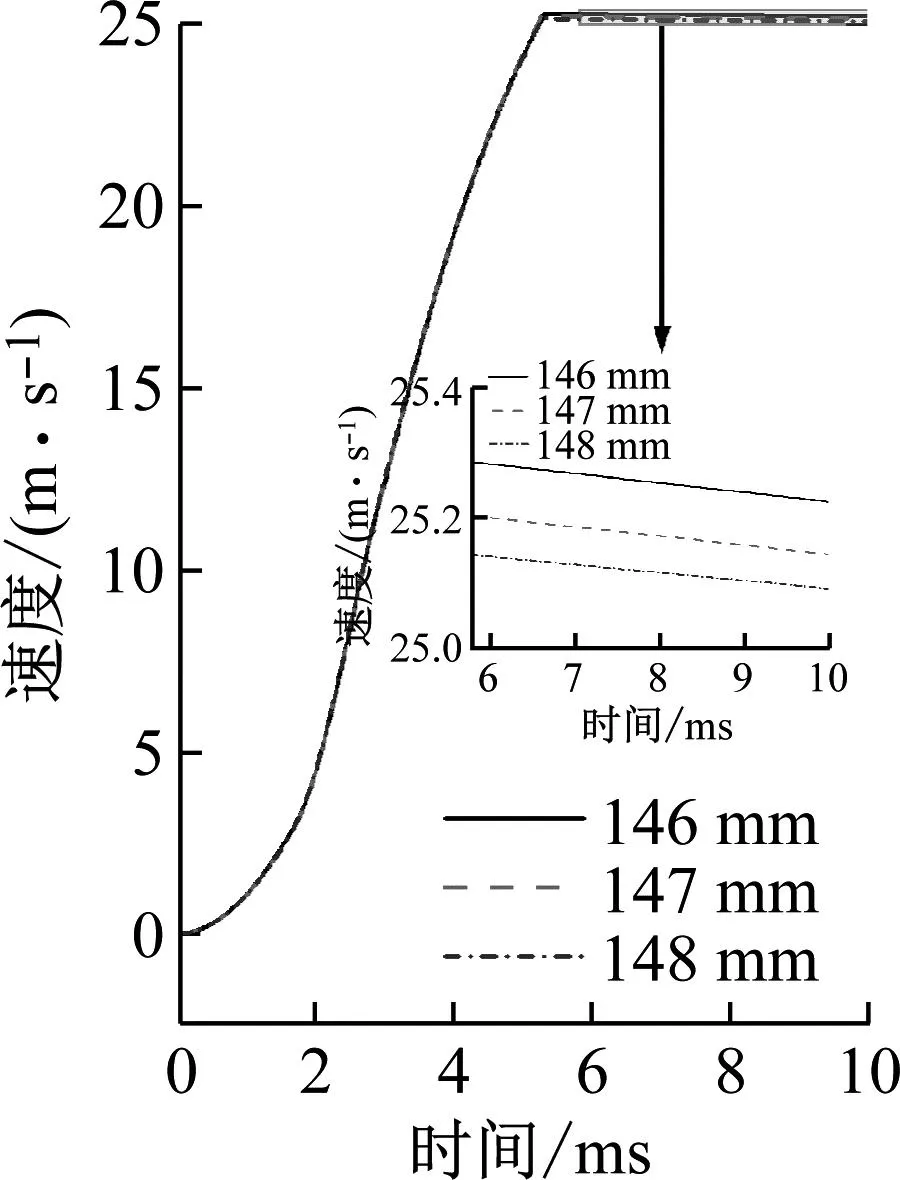
式中,β为子午线平面内流动势椭圆的形状。塑性泊松比vp是单轴压缩时横向塑性应变和纵向塑性应变的比,且-1 当α和β相同时,塑性流是相关的。默认情况下,塑性流是不相关的,允许屈服面和塑性泊松比相互独立的进行校准。如果只知道塑性泊松比,压缩屈服应力比kσ为 (21) 通过铝蜂窝准静态压溃试验得到的载荷与位移曲线,可以得到铝蜂窝的工程应变和工程应力曲线。工程应力所使用的截面面积是试验加载前未受力状态时的截面面积,而实际在加载过程中,材料在轴向变形的时候也伴随着横向变形的出现,导致加载时的真实截面出现变化。真应力一般不能直接通过试验测出,通常通过一系列假设和计算得出来的。对于大多数泡沫材料,其塑性泊松比一般为0,在压溃过程中横向变形很小,通常可以认为泡沫材料在压溃过程中截面面积不发生变化,因此对于泡沫材料来说其真应力等于工程应力 σtrue=σeng (22) 真应变和工程应变之间的关系为 εtrue=ln(lt/l0)=ln(1+εeng) (23) 式中:σtrue为真应力;σeng为工程应力;εtrue为真应变;εeng为工程应力;lt为试件受力变形后的瞬时标距长度;l0为试件的初始标距长度。 由此便得到了铝蜂窝可压碎泡沫塑性模型的全部参数,如表4所示,并将上述真应力真应变的塑性部分作为硬化曲线输入。 表4 铝蜂窝材料属性 按照上述铝蜂窝准静态压溃试验建立仿真模型。可以发现,试验过程中压板和基座的变形很小,可以忽略不计。因此将压板和基座设置为刚体,铝蜂窝采用塑性可压碎泡沫模型。将基座固定,压板以一定的速度压溃铝蜂窝,根据试验建立压板与铝蜂窝、铝蜂窝与基座之间的接触。 由于在相同试验条件下同一规格铝蜂窝的压溃力峰值存在一定差异,并且在实际使用过程中为了消除不同峰值带来的影响,会对铝蜂窝做预压溃处理。因此可认为当试验和仿真的载荷-位移曲线中稳态压溃部分相互吻合时,便可判定该仿真准确。 通过铝蜂窝与基座之间的接触力可以得到仿真过程中铝蜂窝的载荷-位移曲线如图8所示,可以看出仿真和试验的结果基本吻合,在稳态压溃阶段(位移为3~10 mm),试验压溃力平均值为20.044 kN,仿真平均值为19.978 kN,相比于试验,误差为0.33%。在试验中,为了使铝蜂窝可以稳定吸能,对铝蜂窝先进行3 mm预压溃处理,消除渐进屈曲阶段,当铝蜂窝被预压溃3 mm再次压溃时,载荷-位移曲线从弹性阶段开始,经过稳态压溃阶段到密实阶段结束,因此认为不同压溃力峰值不会对平均压溃力产生影响,验证了铝蜂窝塑性可压碎泡沫模型轴向压溃的准确性。 图8 准静态压溃试验与仿真 本文采用ABAQUS/EXPLICT对发射器进行建模仿真,按照发射过程中的实际情况,将发射架固定,在发射腔体、发射腔盖和活塞上施加膛压进行仿真计算,由于其余零部件对发射后坐力的影响较小,且为了加快计算速度,因此将铝蜂窝之外的零部件均设置为刚体。 通过铝蜂窝完全压溃准静态试验可得,铝蜂窝初始高度为12 mm,压溃后的高度为2 mm,压溃速度为2 mm/min,所以准静态试验的应变率为0.002 8 s-1。在发射后坐力试验中,铝蜂窝的初始高度为9 mm,试验结束后的平均高度为3.918 mm,持续时间约为6 ms,因此发射动态平均应变率为93 s-1。 为了降低应变率对仿真准确性的影响,将应变率引入到Cowper-Symonds模型,则铝蜂窝稳态压溃阶段的平台应力为[26] (24) 式中:σm为铝蜂窝的平面压溃强度;vd为动态压溃速度;lh为铝蜂窝胞元边长;D和pd为应变率材料常数,对于3003铝合金,D=24 295.5 s-1,pd=1.094。 为了验证发射后坐力仿真的准确性,进行了发射后坐力试验。试验布局如图9所示。主要由发射器、后坐力传感器、高速摄像和测试设备组成,火工装置发射牵引体,后坐力传感器测量发射过程中作用在其上的力并通过测试设备记录和储存,高速摄像用于记录试验过程并读取发射速度。 图9 后坐力试验布局 为了研究不同药量对同一内径铝蜂窝发射后坐动态特性的影响,通过内弹道模型计算了7.3 g和7.6 g黑火药的内弹道曲线。并将其作为输入条件研究了内径为148 mm的铝蜂窝的发射后坐动态特性。 7.3 g黑火药条件下试验与仿真过程如图10所示。可以看出,两者发射过程几乎一致。火药被点燃后,产生大量高温高压气体。当膛压大于启动压力后,铜销被剪切,牵引体沿发射筒运动。大约6 ms后,牵引体离开发射筒,完成发射。 (a) t=0 试验前后铝蜂窝的情况如图11所示。铝蜂窝状态完好,受力面被压溃形成褶皱,压溃面较为平整。铝蜂窝在试验前后高度变化情况如表5所示。在铝蜂窝每两个孔中间取点,在试验前后测量其高度平均值为3.918 mm,则铝蜂窝平均被压溃了5.045 mm。仿真中发射腔盖的位移最大值为5.473 mm,相比于试验,仿真误差为8.48%。 表5 铝蜂窝高度变化 (a) 试验前 试验测得牵引体的平均速度为21.75 m/s。如图12所示,内弹道和仿真时的牵引体速度分别为22.21 m/s和23.94 m/s。与试验相比,内弹道和仿真速度误差分别为2.3%和10.06%。主要原因是试验中牵引体与发射筒之间有两个密封圈,牵引体运动时,密封圈和发射筒会产生较大的摩擦力阻碍牵引体的运动,导致试验速度小于内弹道和仿真速度。由于速度误差,弹丸位移也存在一定的误差。 图12 内弹道与仿真速度和位移曲线 试验和仿真的后坐力曲线如图13所示。7.3 g火药药量条件下,试验和仿真的后坐力峰值分别为24.133 kN和18.882 kN。稳态压溃阶段(≥15 kN),试验和仿真的平均后坐力分别为19.552 kN和18.583 kN。与试验相比,仿真的最大后坐力误差为21.76%,平均后坐力误差为4.96%。7.6 g黑火药试验和仿真的后坐力峰值分别为22.453 kN和19.221 kN。试验和仿真的平均后坐力分别为19.358 kN和18.953 kN。与试验相比,仿真的最大后坐力误差为14.39%,平均后坐力误差为2.09%。 图13 不同药量下的后坐力曲线 对于后坐力峰值而言,主要取决于铝蜂窝的动态压缩强度,根据式(24)可知,随着后坐速度的增大,动态压溃下铝蜂窝的平台应力增大。如图14后坐速度曲线所示,7.3 g和7.6 g两种火药药量条件下的最大后坐速度分别为2.499 m/s和2.682 m/s,在这两种后坐速度下铝蜂窝的动态压溃强度为2.445 MPa和2.450 MPa,相对应的动态压溃力为21.682 kN和21.726 kN。则可以得到7.3 g和7.6 g两种药量下的最大后坐力误差分别为10.15%和3.23%。 图14 不同药量下的后坐速度曲线 由图13可知,试验与仿真的后坐力曲线初始与结束阶段相差不大。而在稳态压溃阶段,试验后坐力曲线呈现两种趋势,前半段向下振荡,后半段向上振荡。这主要是由于内弹道模型求得的膛压为平均膛压,与实际情况存在一定的差异。随着膛压的增加,发射腔盖的后坐速度增加,根据式(24)可知,随着后坐速度的增大,动态压溃下铝蜂窝的平台应力增大,导致后半段后坐力上升。在仿真中,后坐力在稳态压溃阶段保持恒定,这与试验中的振荡现象存在差异,但这些差异只占平均后坐力的4.56%,因此可以认为仿真是准确和可靠的。 同时也可以发现,随着药量的增大,后坐力峰值从18.882 kN增加到19.221 kN,增加了1.79%;平均后坐力从18.583 kN增加到18.953 kN,增加了1.95%。主要原因是随着药量的增加,膛压增大,即作用在发射腔盖上的力增大,使得后坐速度增大,导致铝蜂窝的平面压溃强度增大,但是由于药量变化较小,因此后坐力变化不大。 牵引体的速度曲线和发射腔盖后坐位移曲线如图15所示。可以发现药量增大,发射速度由23.871 m/s增大到25.088 m/s,增大了5.10%;后坐位移由5.473 mm增大到5.891 mm,增大了7.64%,即铝蜂窝被压溃的高度增大。由图4可得,7.3 g药量牵引体离开发射筒的时间为6.05 ms,7.6 g药量牵引体离开发射筒的时间为5.92 ms。当牵引体离开发射筒后药室内部形成一个密闭腔体,该腔体内部压力平衡,作用在发射腔盖上的力降为零。由于7.6 g药量牵引体速度大,离开发射筒的时间缩短,因此后坐力持续时间减短。 图15 不同药量下发射与后坐位移速度曲线 为了研究铝蜂窝横截面积对发射后坐动态特性的影响,进行了内径为146 mm、147 mm和148 mm的铝蜂窝缓冲垫在7.6 g黑火药下的仿真与试验。得到了三种内径下的后坐力曲线如图16所示。结合表6可得,相比于内径为148 mm的铝蜂窝,内径为147 mm和146 mm的后坐力峰值分别增加了4.63%和9.90%,平均后坐力分别增加了4.06%和9.08%。主要原因是随着铝蜂窝内径的减小,横截面积增大,因此铝蜂窝的平面压溃力增大,后坐力相应的增大。 表6 仿真结果 图16 不同横截面积下后坐力曲线 由图16可知,内径为146 mm时:试验和仿真的后坐力峰值分别为27.831 kN和21.124 kN;试验和仿真的平均后坐力分别为22.068 kN和20.674 kN;仿真的后坐力峰值和平均值误差分别为24.10%和6.31%。内径为147 mm时:试验和仿真的后坐力峰值分别为23.848 kN和20.110 kN;试验和仿真的平均后坐力分别为19.031 kN和19.722 kN;仿真的后坐力峰值和平均值误差分别为15.674%和3.63%。 根据4.2节关于后坐力峰值的分析对不同内径铝蜂窝的动态压溃强度进行计算。如图17后坐速度曲线所示,内径为146 mm、147 mm和148 mm的铝蜂窝的最大后坐速度分别为2.581 m/s、2.792 m/s和2.682 m/s,在这三种后坐速度下铝蜂窝的动态压溃强度为2.448 MPa、2.453 MPa和2.450 MPa,相对应的动态压溃力分别为21.702 kN、21.753 kN和21.726 kN。则可以得到上述三种工况下的最大后坐力误差分别为22.02%、8.78%和3.23%。 图17 不同横截面积下后坐速度曲线 上述分析考虑了后坐力峰值与后坐加载速度的影响,然而后坐力峰值还与火药性能参数、发射环境温度和铝蜂窝加工精度等因素密切相关。其中对于火药性能而言,能量大时会使得膛压增大,后坐力增大;对于环境温度而言,高温使得膛压增大,铝蜂窝变弱,低温使得膛压降低,铝蜂窝增强;对于铝蜂窝加工精度而言,其有效胞元个数影响铝蜂窝的平面压溃强度,进而影响后坐力峰值。 牵引体的速度曲线和发射腔盖后坐位移曲线,如图18所示。可以发现随着铝蜂窝内径的增大,牵引体发射速度降低,后坐位移增大,即铝蜂窝被压溃的高度增大。根据表6可得,相比于内径为148 mm的铝蜂窝,内径为147 mm和146 mm的牵引体发射速度分别增加了0.22%和0.54%,后坐位移分别减小了3.38%和15.24%。主要原因是随着铝蜂窝内径的增大,其平面压溃强度降低,在药量不变的情况下,后坐位移增大,导致牵引体的速度降低。 图18 不同横截面积下发射与后坐位移速度曲线 (1) 通过黑火药密爆试验建立了定容内弹道模型,求解得到了燃速系数和火药力,在此基础上通过可变体积内弹道模型求解得到不同药量下的内弹道特性,结果表明在火药质量增大0.3 g的情况下,峰值膛压增大了3.82%,牵引体的速度增大了1.80%。 (2) 通过铝蜂窝准静态试验与塑性可压碎泡沫模型建立了准静态压溃有限元仿真模型,当铝蜂窝结构内径从148 mm分别减小1 mm和2 mm,其有效胞元个数增加,进而使得稳态压溃力分别增大0.75%和4.35%。 (3) 研究了火药药量和铝蜂窝内径对发射后坐特性的影响。结果表明:火药药量增大0.3 g,后坐力平均值增大了1.95%、牵引体发射速度增大了5.10%,后坐位移增大了7.64%,后坐力持续时间减小10.3%。当铝蜂窝内径从148 mm分别减小1 mm和2 mm时,后坐力平均值增大了4.06%和9.08%,牵引体发射速度增大了0.22%和0.54%,后坐位移增大了3.38%和15.24%。
4 发射后坐特性试验验证与多参数仿真分析
4.1 后坐动力学仿真模型与试验布置

4.2 不同药量对发射后坐动态特性的影响

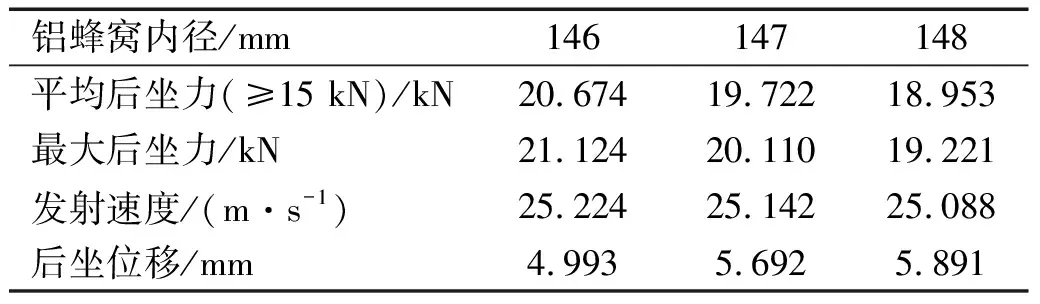
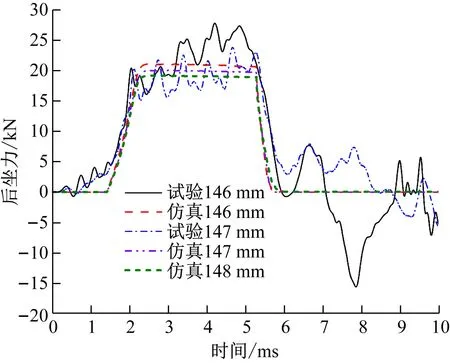
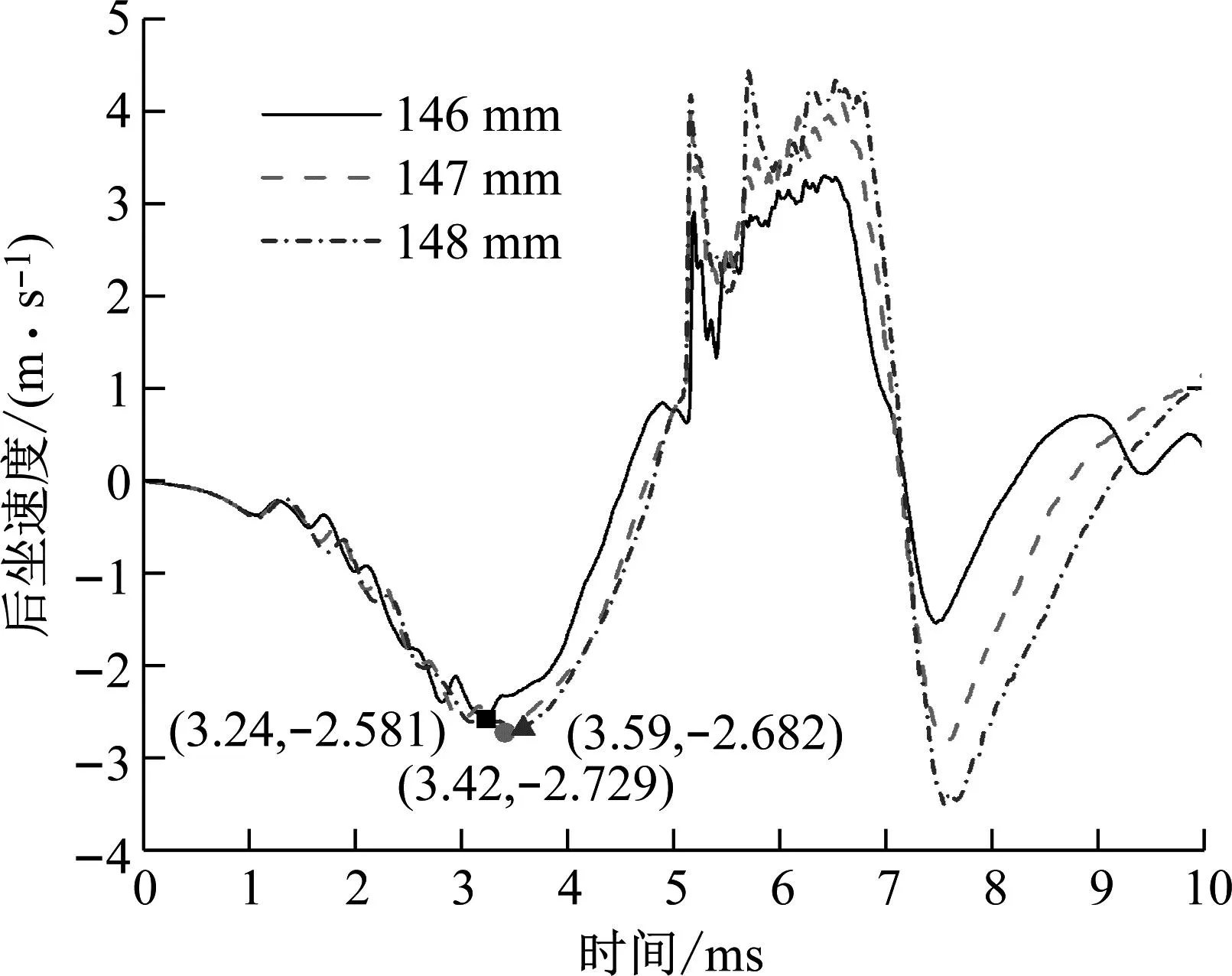
4.3 铝蜂窝横截面积对发射后坐动态特性的影响
5 结 论

