基于比例边界有限元法计算应力强度因子的不确定量化分析

胡昊文,陈灯红,王乾峰,胡记磊,骆 欢

(1.防灾减灾湖北省重点实验室(三峡大学),湖北 宜昌 443002;2.三峡大学 土木与建筑学院,湖北 宜昌 443002)

裂纹存在于众多结构中,例如混凝土结构通常是带裂缝工作的,岩块表面存在着许多裂隙,等。断裂问题一直都是计算固体力学的难点和重点。其中,应力强度因子是预测载荷作用下结构中裂纹的产生和扩展的重要参数。分析断裂问题时,有限元法(finite element method,FEM)以其成熟的商用性和对不同边界、不同荷载状况下的普遍适用性成为求解断裂问题最主要的数值方法。但传统有限元法在处理断裂问题时会面临一些挑战。比如三角形或四边形单元不能准确地计算裂纹尖端的奇异应力,并且裂纹尖端的网格需要几个数量级的加密。一些学者使用边界元法[1-2](boundary element method,BEM)来处理断裂问题。边界元法只需离散结构表面,将问题的维数减少一维。其作为一种半解析法,边界元法能够更准确地计算应力强度因子。对于复杂问题,边界元法所需的基本解很难解析获得甚至是不存在,同时积分方程还会产生奇异积分。这些困难限制了边界元法的发展。

Song等[3-4]提出的比例边界有限元法(scaled bountary finite element method,SBFEM),是一种新的半解析数值方法,它克服了传统有限元法的一些局限性,并借鉴边界元法的思想,只在结构表面进行离散,将问题维数减少一维,辐射边界条件自然满足,且不需要基本解。这些优势使其成为学者们所青睐的一种数值方法。该方法已成功应用于无限域问题[5-8]、断裂力学[9-12]、波传播[13-14]、接触问题[15]等多个领域,关于SBFEM最新研究详见相关综述[16]。当处理线性断裂力学时,任何类型的奇异应力都能解析表示,且不需要局部细化和富集函数[17]。此外,比例边界有限元法多边形单元的形函数包含奇异项,可以准确地表征应力集中系数[18]、应力强度因子[19]和T-应力[20]。

目前成熟的数值算法,大都是基于确定性的分析。然而,在工程问题中存在诸多不确定性因素,例如结构的几何尺寸,材料自身的力学参数,荷载的随机性等等。若忽略这些因素的影响,可能会导致结构失效,甚至引发灾难性的后果。综合考虑不确定性因素,使数值分析更符合实际工程,不确定性量化[21](uncertainty quantification,UQ)分析成为近些年的热点方向。

不确定量化本质上是研究输入的不确定造成的输出不确定。针对这一特点,学者们处理不确定量化分析的步骤主要分为三步。第一步:构建物理模型。不确定量化的结果取决于高精度的数值模型。这一步通常采用成熟的确定性算法,诸如有限元法、边界元法、比例边界有限元法等。不确定量化与这些数值算法结合,产生了随机有限元法、随机边界元法等经典研究方法。第二步:描述不确定性参数。通常使用随机变量或随机场。例如摄动法,将一个随机函数在其均值附近进行Taylor展开,然后对其进行合理的截断;多项式混沌展开,在随机参数空间对精确解作一个有限阶多项式展开,求解相关系数以获得精确解的全部信息;蒙特卡罗模拟(Monte Carlo simulation,MCS)[22-23],假设随机变量所遵循的概率分布,通过计算随机抽样的样本响应,获得统计特征(期望、标准差等)。第三步:将随机变量或随机场导入数值模型中,进行不确定性传播,得到高阶矩、概率密度函数、累积密度函数等统计特征,用于评估不确定性参数对结构响应的影响。

描述不确定性参数步骤中,蒙特卡罗模拟方法以其思想简单和广泛适用成为很多学者首选的方法。此外,蒙特卡罗模拟的收敛速度只与随机采样次数N有关,而与求解问题的维度无关。所以,在很多高维问题的求解过程中,蒙特卡罗方法往往是最合适的甚至是唯一的选择。处理工程问题时,单点响应计算耗时严重,执行大量采样来确保蒙特卡罗模拟收敛的成本是无法负担的,直接的蒙特卡罗模拟不得不与其他方法相结合,以节约计算成本,提高计算效率。Gu[24]从硬件方面减少硬件资源消耗、提高硬件计算的并行性和加速性能,从而减少蒙特卡罗模拟硬件方面的成本;Fishman[25]优化蒙特卡罗模拟采样策略,一定程度上减少了取样个数,降低了计算量;Ding等[26]使用模型降阶算法加速蒙特卡罗模拟过程,分析结构的高维不确定性。

本文构建一种新颖的基于比例边界有限元法求解断裂问题的不确定量化分析方法。首先,采用比例边界有限元法计算应力强度因子(stress intensity factor,SIF);然后,使用蒙特卡罗模拟进行不确定量化分析,并对直接的蒙特卡罗模拟进行改进;最后采用奇异值分解,构造低阶的子空间,用径向基函数对子空间进行近似,通过子空间线性组合获得新的结构响应,实现基于MCS的快速不确定量化分析。

1 基于比例边界有限元法的蒙特卡罗模拟

1.1 比例边界有限元法

Wolf等详细介绍了比例边界有限元的推导过程,本文只给出一些必要的公式。在二维域中给出SBFEM所需的局部坐标,如图1所示。选择一个点O作为比例中心,对比例中心的唯一要求是S的整个边界可视。径向局部坐标ξ,也被称作比例因子,从比例中心指向边界上任意一点。η为环向局部坐标。这种由比例系数和单元局部坐标定义的转换关系称为比例边界转化,并且这种转化关系是唯一的。对于有限域,0≤ξ≤1,而对于无限域,1≤ξ≤∞。在(η,ξ)点处的位移可以用分段插值来近似

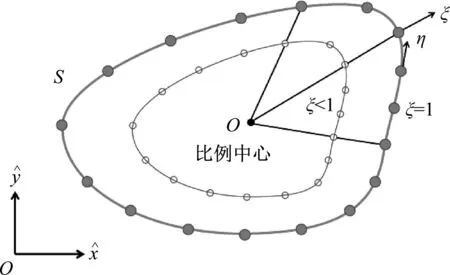
图1 比例边界有限元的坐标系统

{u(ξ,η)}=[N(η)]{u(ξ)}=[N1(η)[I],

N2(η)[I],…]{u(ξ)}

(1)

式中:[N(η)]为在环向上的形函数;u(ξ)为沿径向线的位移函数,仅与ξ有关;[I]为一个2×2的单位矩阵。

应变表示为

{ε(ξ,η)}=[B1(η)]{u(ξ)},ξ+

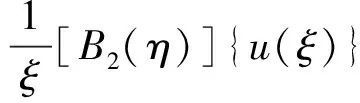
(2)

式中,[B1(η)]和[B2(η)]为节点应变与位移的关系。

应力表示为

(3)

式中,[D]是弹性矩阵。

在比例边界坐标中表示控制微分方程后,可以在径向ξ上运用伽辽金法或虚功原理,得到基于位移的二维比例边界有限元法的基本方程

[E0]ξ2{u(ξ)},ξξ+([E0]-[E1]+[E1]T)ξ{u(ξ)},ξ-

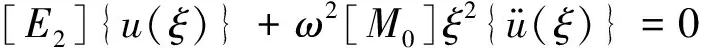
(4)

式中,当频率ω=0,式(4)为静力平衡方程。矩阵[E0]、[E1]、[E2]和[M0]是组装边界(ξ= 1)上计算的单元系数矩阵获得,其形式为

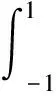
(5)

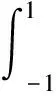
(6)

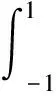
(7)

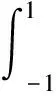
(8)

值得说明的是,[E0]、[E1]和[E2]与常规有限元中静力刚度阵相似,而[M0]类似于质量阵。其中,[E0]、[M0]是正定矩阵,[E2]是半正定矩阵,而[E1]是非对称。式(4)是Euler-Cauchy方程,可解析求解。

1.2 计算应力强度因子

求解式(4)后,可以获得节点位移。通过位移场可以提取应力强度因子。位移场的渐进解表示为

{u(ξ)}=[V11]ξ-[S11]{c}+O{ξ2}

(9)

式中:{c}为边界积分常数;O{ξn}为一个高阶项,在相同的ξn下趋于零,它包含高频下惯性力的影响;[S]和[V]为式(4)转化为一阶常微分方程求解过程中Hamilton矩阵进行Schur分解时产生的特征值和特征向量[27];[S11]为包含所有非正特征值;[V11]为对应的特征值向量。代入到式(9)得

{u(ξ)}=[ψ(r)]{c(r)}+[ψ(s)]ξ-[S(s)]{c(s)}+

[ψ(T)]ξ{c(T)}+[ψn1]ξ-[Sn1]{cn1}+

O{ξ2}

(10)

位移的导数求解为

{u(ξ)},ξ=-[ψ(s)][S(s)]ξ-[S[s]]-[I]+

[ψ(T)]{c(T)}-[ψn1][Sn1]ξ-[Sn1]-[I]{cn1}+

O{ξ}

(11)

其中,积分常数{c}表示为

{c}={{cn1};{c(T)};{c(s)};{c(r)}}

(12)

在一个线单元的指定局部坐标ξ处,应力场表示为

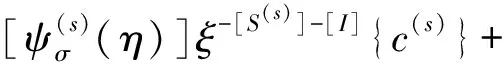
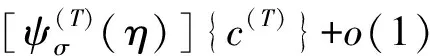
(13)

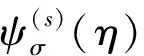
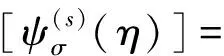
[B2(η)][ψ(s)]),

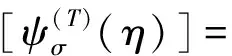
[B2(η)][ψ(T)])

(14)

奇异点周围应力的渐近解表明,动力学中奇异应力和T-应力的定义与静力学相同。图2给出了基于SBFEM多边形裂纹模型,其中笛卡尔坐标系和极坐标系的原点位于裂纹尖端。对于均质板中的裂纹和各向同性双材料板中的界面裂纹,应力强度因子统一定义为

(15)

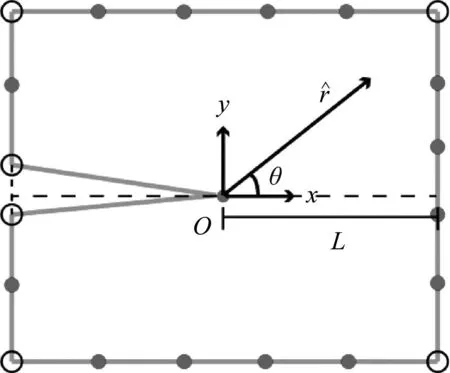
图2 裂纹区域的离散(比例中心位于裂纹尖端)

并且

(16)

式中:L为特征长度,应力强度因子的幅值与L无关;ε为两种材料的振荡系数,只与材料本身有关。

(17)

式中,r(θ)为从比例中心到沿角度(θ)径向线的边界的距离(图2)。将ξ的矩阵幂函数改写为极坐标形式

(18)

使用式(17),将奇异应力式(13)从局部坐标转换为极坐标形式

(19)

根据式(15)中应力强度因子的形式,广义应力强度因子表示为

(20)

通过式(20)可以很容易地计算任意(θ)角度下应力强度因子,并且对于确定裂纹扩展是非常重要的。

1.3 蒙特卡罗模拟

进行蒙特卡罗模拟之前,首先简要介绍带有不确定性参数的控制方程。设整个分析域为Ω,边界为Γ(Γ=Γu+Γt),假定弹性模量E为不确定性参数,即

{σ(E)}ij,j+{f}i-ρ{u(E)}i,tt-μ{u(E)}i,t=0

(21)

对于静力学问题略去后两项的惯性力和阻尼力,边界上的约束条件为

(22)

(23)

式中,{ε}为应变。则应力为

{σ(E)}ij=[D(E)]ijkl{ε(E)}kl

(24)

使用伽辽金方法,运用分部积分和边界条件,可以得到带有随机参数的弱形式

(25)

使用比例边界有限元法进行离散,得到带有随机参数的代数方程

(26)

式中:{d}为节点位移向量;{F}为荷载向量;[M]、[C]和[K]分别为全局质量矩阵、阻尼矩阵和刚度矩阵。值得注意的是,这里假设弹性模量作为随机参数存在于每个单元刚度矩阵中,用随机场f(x)来描述弹性模量,对于每个单元有

(27)

式中:[B]为位移微分矩阵;J为雅可比矩阵。将式(25)中的[B]转化为相应的系数矩阵[E],得到带有不确定参数的比例边界有限元方程。(对于静力学问题,略去质量阵和阻尼阵。)随后基于蒙特卡罗模拟的思想,将随机变量依次代入系统中进行求解,通过式(28)和(29)计算统计特征,以评估不确定参数对结构响应的影响,即

(28)

(29)

式中:N为样本个数;{d(j)}为第j个样本点的结构响应。蒙特卡罗模拟的收敛速度为O(N-1/2),N越大,蒙特卡罗模拟收敛效果越好,计算成本也就越高。为了降低计算成本,提高计算效率。第2章将使用模型降阶法,对直接的MCS进行加速求解。

2 奇异值分解

根据初始样本的波动范围,引入m个随机变量并计算其响应,将这些样本点的响应[d(αm)]按列排列,构造快照矩阵[Ω][28]

[Ω]=[d(α1),d(α2),…,d(αm)]=

(30)

式中:[Ω]∈Rn×m;n为单个输入变量下的响应个数;m为变量个数。使用奇异值分解法(singular value decomposition,SVD)将矩阵[Ω]分解

(31)

式中:r=min(m,n);[U]∈Rn×n、[V]∈Rm×m为正交矩阵;uj和vj分别为[ΩΩT]和[ΩTΩ]的特征向量。[Σ]∈n×m是一个对角矩阵,对角元素σj按从大到小排列。定义[ψj]=uj,[ζj(αi)]=σjvij,式(31)可以改写为

(32)

式中:[ψj]为正交基;[ζj(αi)]为相应的基底。使用式(32),系统响应可以通过简化表达的[ψj]和[ζj(αi)]的线性组合来表示,且其规模比初始模型要小得多。为了实现对任意随机输入变量的系统响应的连续近似,应用径向基函数(radial basis function,RBF)来对降阶子空间中的基底进行插值

(33)

式中:φ为基函数;χ为其权系数。本文选取高斯核函数作为基函数,如下

(34)

(35)

值得注意的是,根据样本点不同,上述方程组是无条件非奇异的。将式(33)代入式(32),式(32)改写为

(36)

可以看出任何系统响应都可以通过使用这种线性组合来近似,无须通过SBFEM进行完整地计算。(当然,快照矩阵的形成仍然需要完整的计算)。图3给出了本文算法的流程图。与直接MCS相比,奇异值分解降低了系统的自由度,并提供了一个低阶模型。RBF计算相关系数,将子空间线性组合获得新的响应。SVD-RBF提高了计算效率,降低了计算成本,这些优势一定程度上扩展了MCS的适用性。

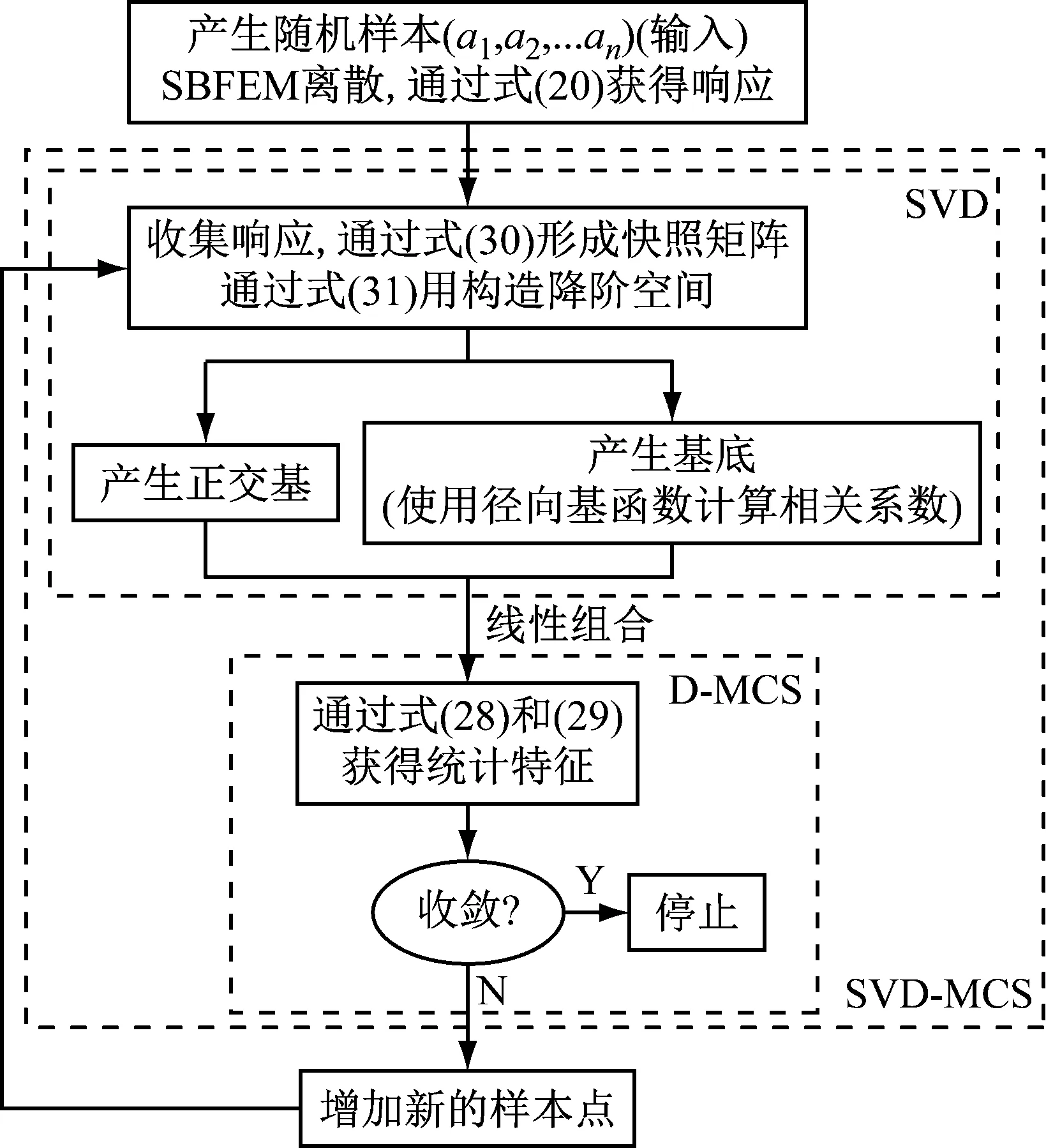
图3 算法的流程图

3 数值算例

3.1 带斜裂纹的平面板

图4考虑一个在y方向,受拉力作用的带有斜裂纹的平面板。其解析解[30]为

(37)

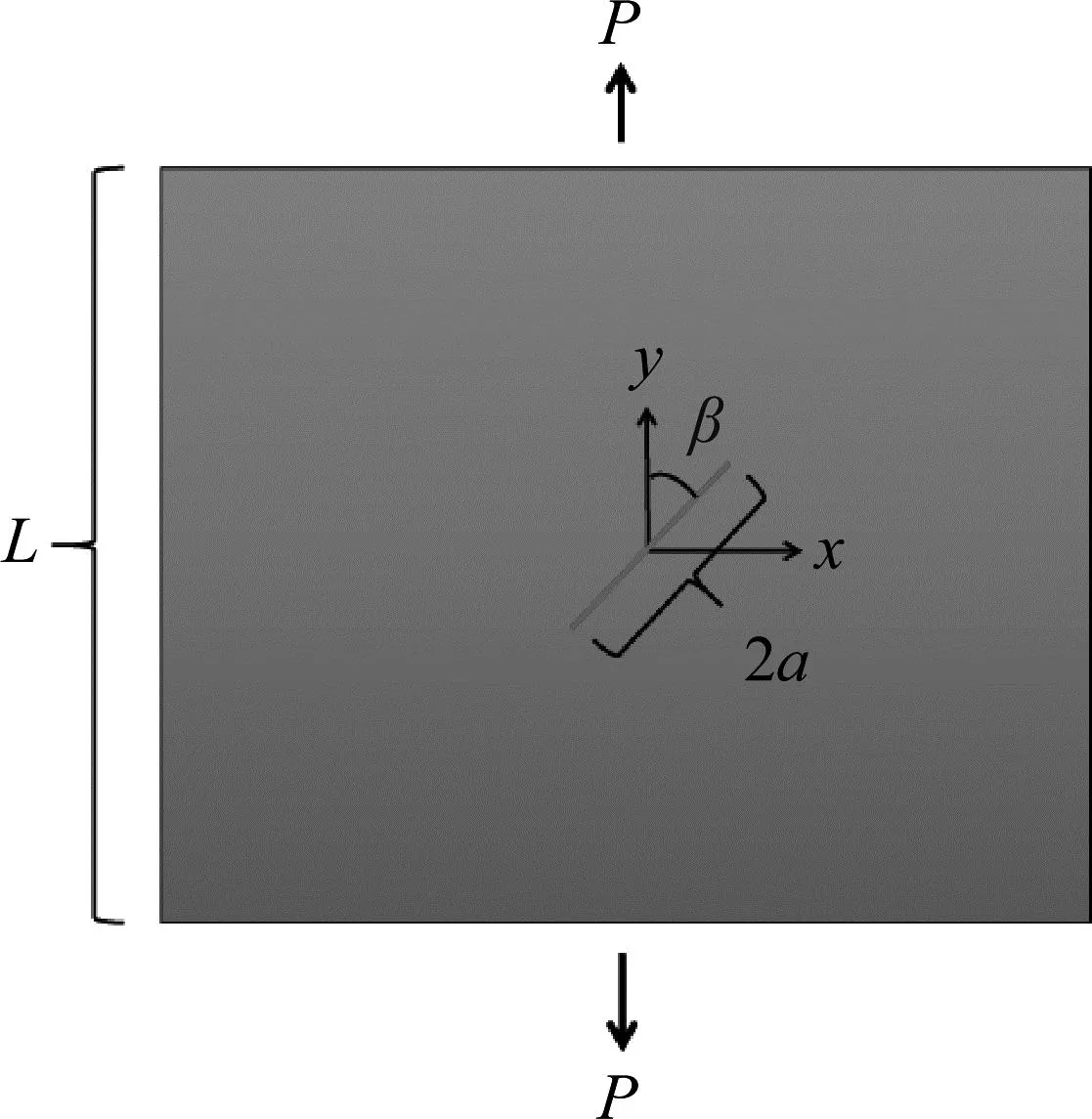
图4 带斜裂纹的平面板模型

式中,P为y方向施加的载荷。a是裂纹一半的长度;β是垂直方向与裂纹之间的夹角。弹性模量E=1 Pa,泊松比v=0.3,矩形板长度L=1 m。

表1给出了三种不同的变异系数下形成快照矩阵的样本点数。并引入R2来评估所提出的方法的准确性,其计算公式为

(38)

表1 不同变异系数条件下本文算法结果的精度

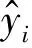
为了更直观地展示算法的精度,图5给出了不同变异系数下的算法解和解析解的比较。从图中可以看到,变异系数控制着变量波动的范围(变异系数越大,数据波动越大)。在各种变异系数下,本文算法与解析解吻合较好。结合表1,可以得出变异系数越大,保持算法精度所需的初始样本点也就越多。初始样本点的数目决定着计算效率,所以平衡计算效率与计算精度是值得注意的。

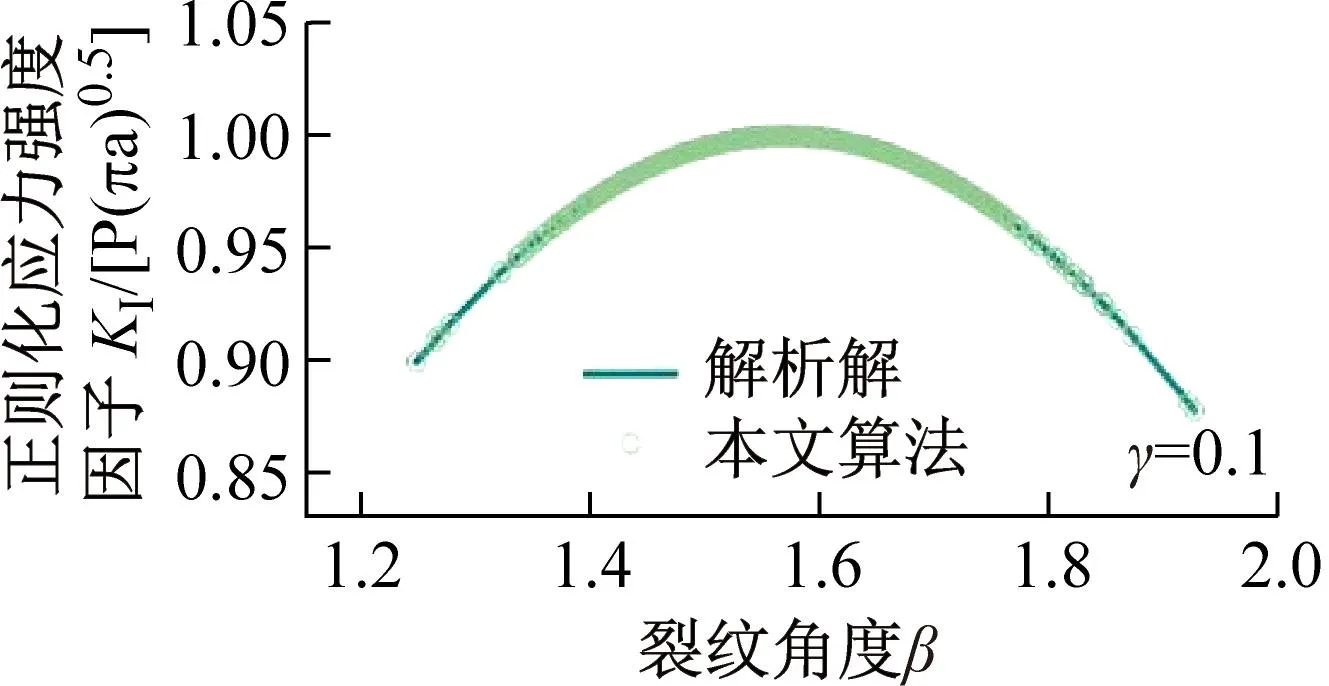
图5 不同变异系数的预测值与解析解的比较

随机分析之前,会进行奇异值分解,此时产生了[Σ]矩阵。该矩阵只有主对角线上存在元素,并且从大到小排列。这些元素称为奇异值,衰减迅速。奇异值越大包含的系统信息就越多,所以截断[Σ]矩阵是必要的,以节省储存空间,提升计算效率。仍使用算例1的初始样本,并采取三种方案进行随机性分析。

方案1:使用SBFEM计算1 000个随机变量下的KI直接进行蒙特卡罗模拟。该计算需要重复1 000次。

方案2:对表1中的原始快照矩阵进行奇异值分解,截断[Σ]矩阵,将[Σ]矩阵维数选择为行与列的最小值。再进行蒙特卡罗模拟。

方案3:在方案2的基础上,[Σ]矩阵维数选择为σcat=10-1σmax。

图6给出了KI在不同变异系数下的统计特征。从图中可以看出方案1与方案2较为吻合,方案3具有一定的误差。这是由于方案3截断了过多的奇异值,导致降阶系统“失真”。为了避免系统失真,保留降阶优势,下面的算例都采用方案2的截断方案。

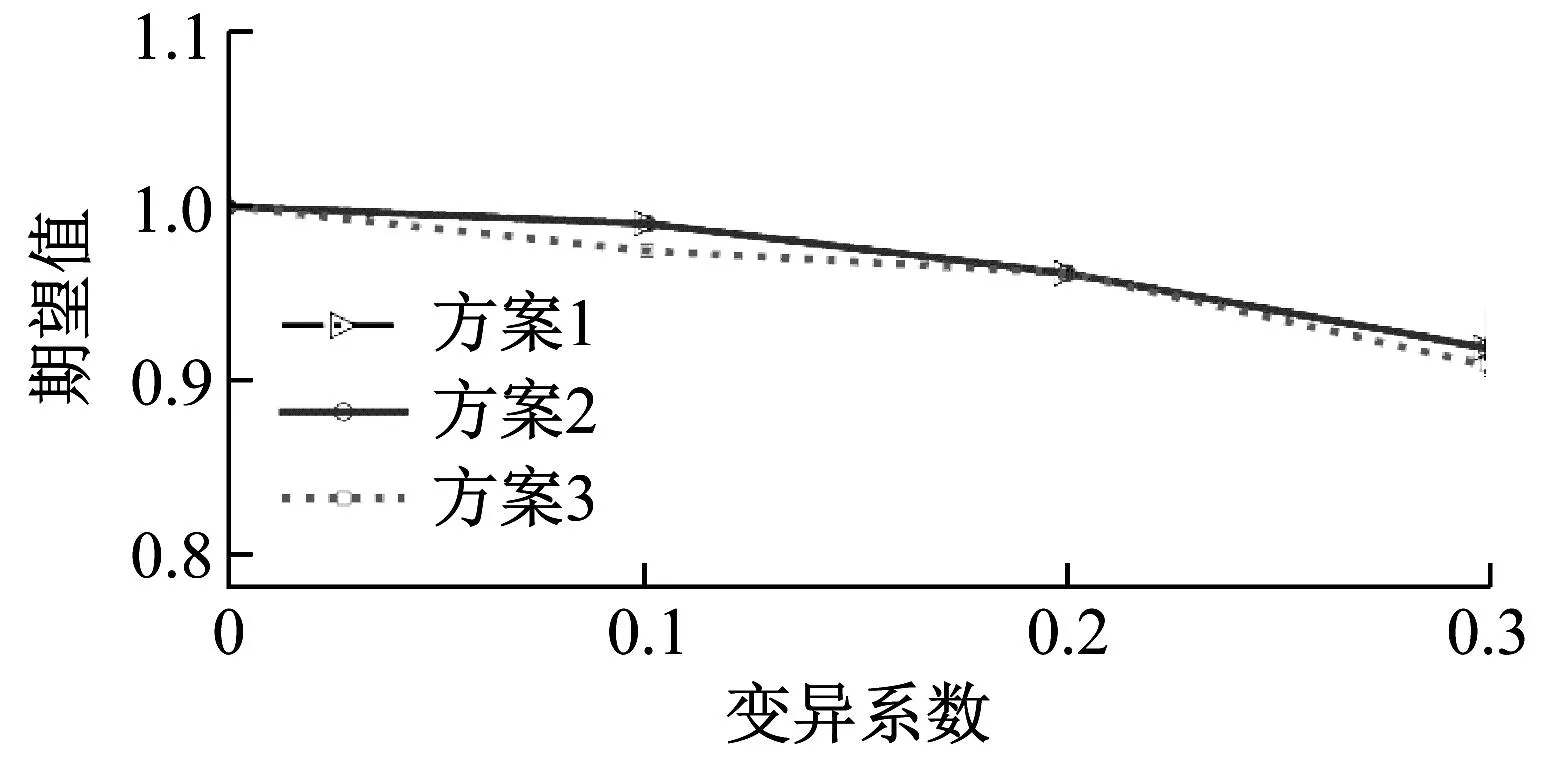
图6 不同方案下KI的统计特征

3.2 平面板中心弯曲裂纹

本节考虑一个中心带有弯曲裂纹的平面板问题[32]。其模型如图7所示,半径和中心裂纹角由r和θ定义。本例中,假设r/w=0.1,取r=4.25 m,上下边界

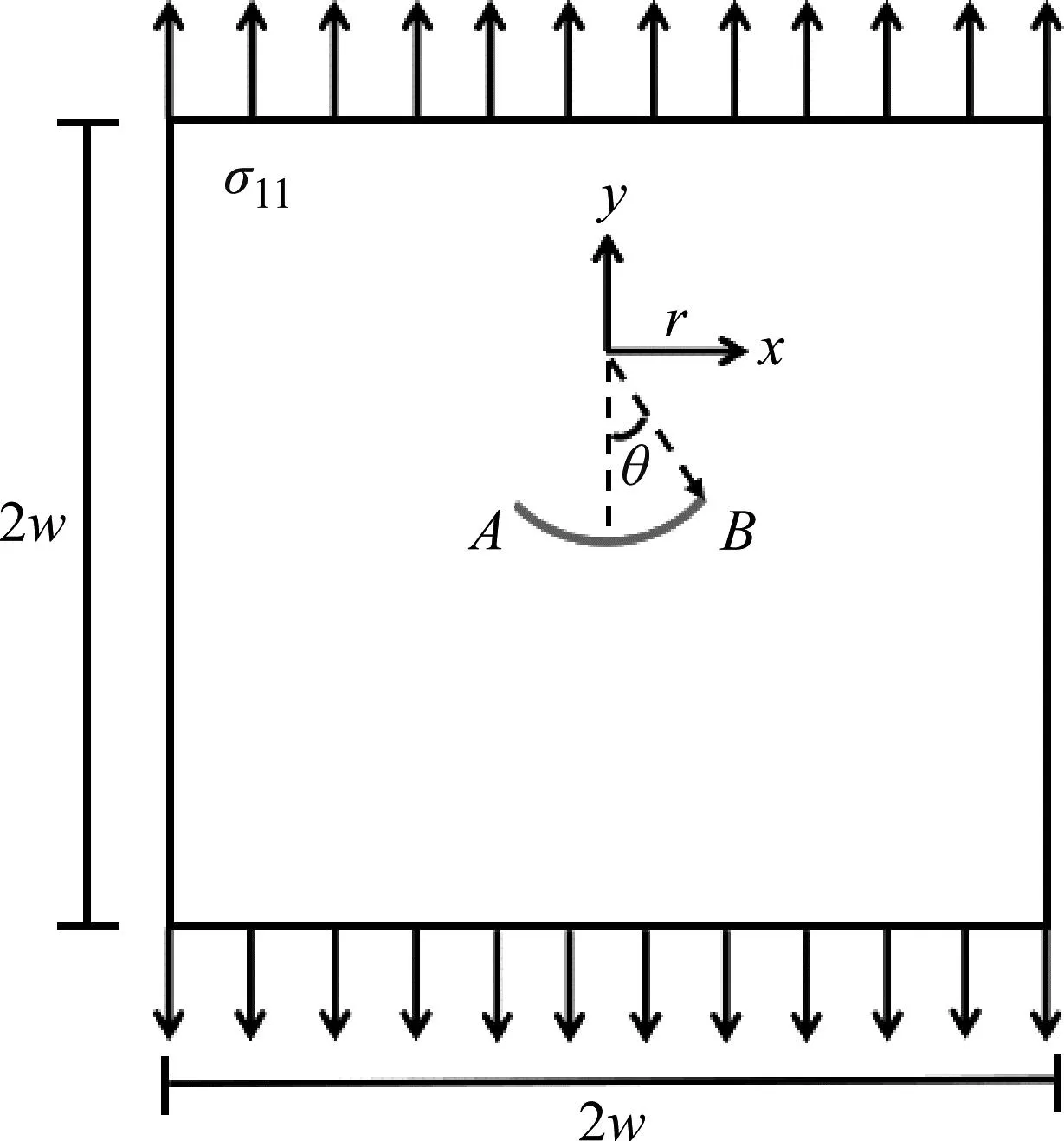
图7 中心弯曲裂纹平面板

受均布荷载作用,计算采用平面应变假定。该问题具有解析解,应力强度因子为

(39)

以应力强度因子KI、KII和节点位移作为响应构造快照矩阵,并对应力强度因子归一化处理。选取初始裂纹角度作为随机输入变量,且服从期望μ= π/6,和标准差为σ=2的正态分布。设置分布参数后,使用随机数生成器,随机生成100个随机角度变量,代入到解析解中进行计算,作为蒙特卡罗模拟的参考解。图8给出了本文算法与解析解的应力强度因子KI,KII的对比。从图中的结果来看,本文的算法与解析解的结果吻合得很好,表明算法具有较高的精度。值得注意的是,降阶算法只采用了35个初始样本点来形成快照矩阵,即只使用了35个样本点,获得了100个该变量下的响应结果,也说明了该算法在计算效率上具有优势。表2具体给出了该算法与基于SBFEM的蒙特卡罗模拟的统计特征和计算成本。表2中的快照矩阵由应力强度因子和98个节点位移构成,自由度的计算方式为变量个数乘以模型自由度。从表2可以看出,本文算法降低了系统自由度,加速了传统的基于SBFEM的蒙特卡罗模拟过程,提高了计算效率。

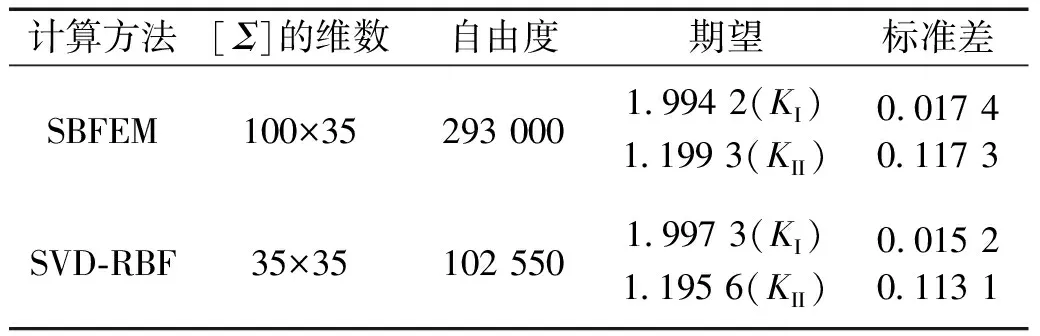
表2 SBFEM与SVD-RBF进行随机分析的计算成本

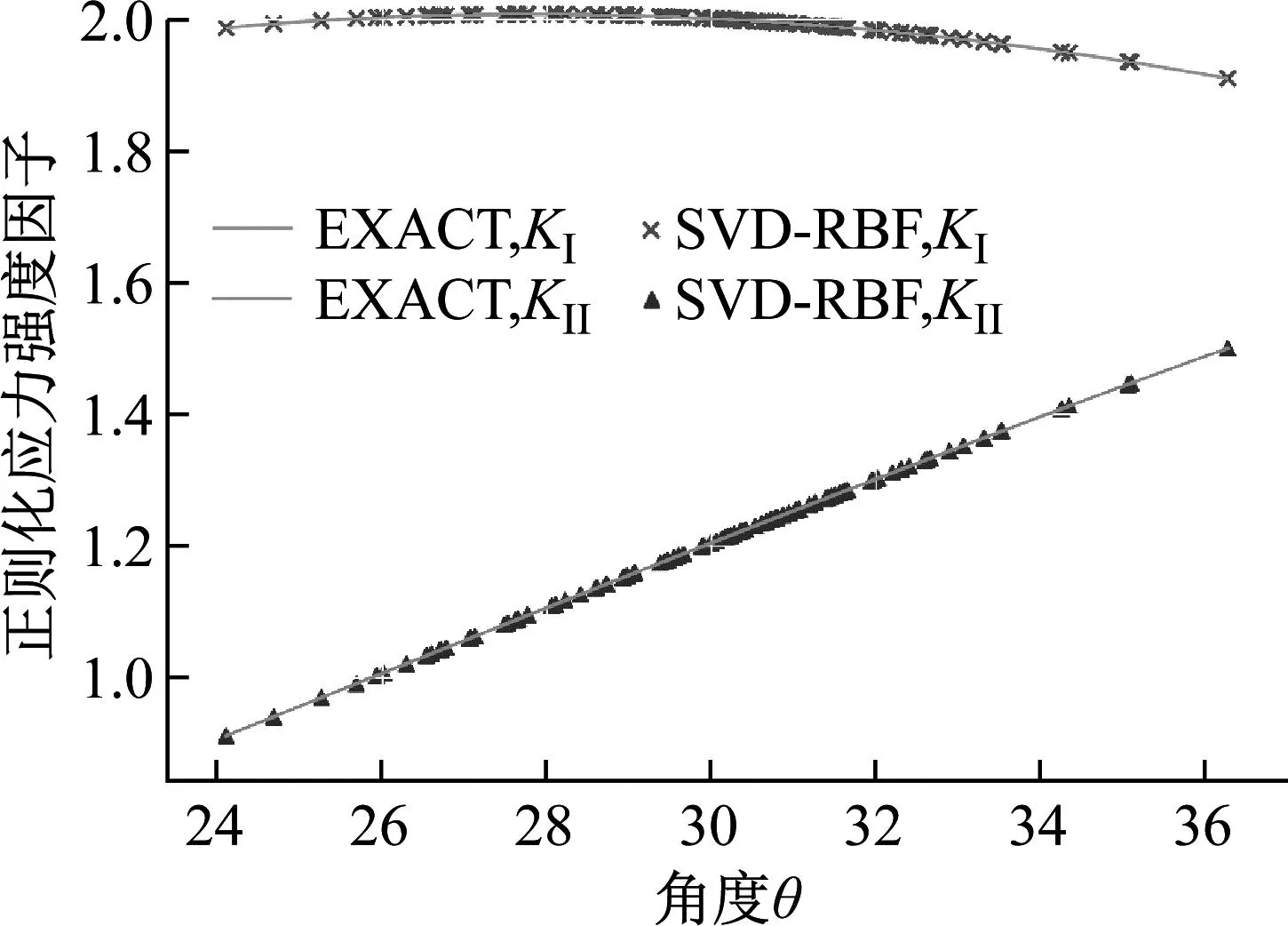
图8 应力强度因子的算法解与解析解的比较

3.3 带孔洞的双裂纹矩形板

本节考虑一个带有圆孔的矩形板,设圆孔半径r为不确定变量,研究其对动态应力强度因子(dynamic stress intensity factor,DSIF)的影响。矩形板的宽度为2b=30 mm,长度为2h=60 mm,包含一个半径为r的孔,在圆孔处有两条与水平方向呈30°夹角的等长度裂纹,如图9(a)所示。其材料特性分别为:密度ρ=5×10-6kg/mm3、泊松比v=0.3,剪切模量G=76.923 GPa。t=0时,板的上下两端受到均布的阶跃荷载p(t)=PH(t)的作用,其中P是荷载的幅值。采用平面应变假定。

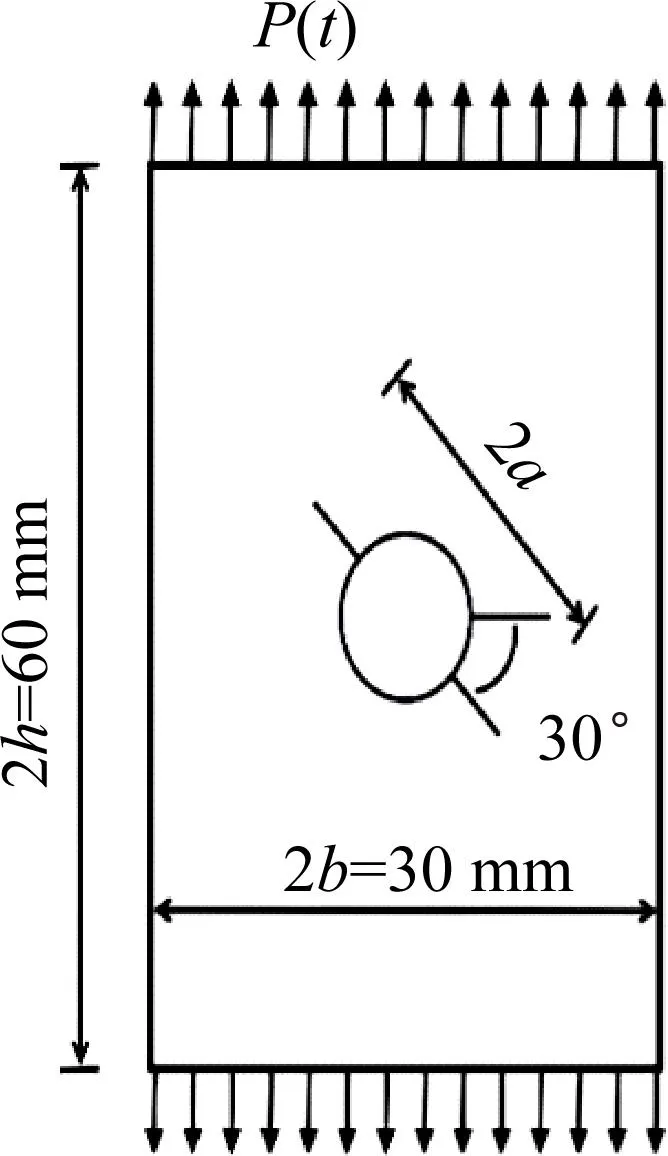
(a) 几何尺寸

使用多边形比例边界有限元法分析时,将该模型划分为8个多边形单元,如图9(b)所示。多边形C1和C2是包含两个裂纹的单元,并且将比例中心设置为裂纹的尖端。对于其他单元,都采用八节点的高阶单元进行离散,用正方形来表示每个单元两端的节点。网格划分完毕后,进行随机性分析。将圆孔半径设为不确定变量,且满足均值为μ=3.6,标准差为σ=0.2的正态分布。使用随机数生成器产生50个满足该分布的随机变量,导入到模型中进行计算,获得50个变量下的动态应力强度因子作为蒙特卡罗模拟的参考解。其中,计算动态应力强度因子的总时间为20 μs,计算时间步长Δt=0.1 μs。

图10和11给出了降阶算法与蒙特卡罗模拟得出的统计特征的对比。从图中的结果来看,本文的算法与蒙特卡罗模拟结果吻合得很好。值得注意的是,降阶算法只采用了17个初始样本点来形成快照矩阵。意味着降阶算法只使用了17个样本点,获得了50个蒙特卡罗模拟的结果。为了使数据更具说服性,图12给出了r=3.75 mm时,算法的结果与参考解的对比。其中,这里r=3.75 mm是算法预测值,而非初始样本点。从图12可以看出,算法预测的结果与参考解基本保持一致。此外,快照矩阵还使用奇异值分解进行降维,进一步节省储存空间。为了更清晰地说明算法的优越性,表3给出了基于SBFEM分析断裂问题的框架下,本文算法与直接的蒙特卡罗模拟的计算成本的对比。总的来说,本文算法提高了传统蒙特卡罗模拟的计算效率,拓展了蒙特卡罗模拟的适用性。

表3 SBFEM与SVD-RBF进行随机分析的计算成本

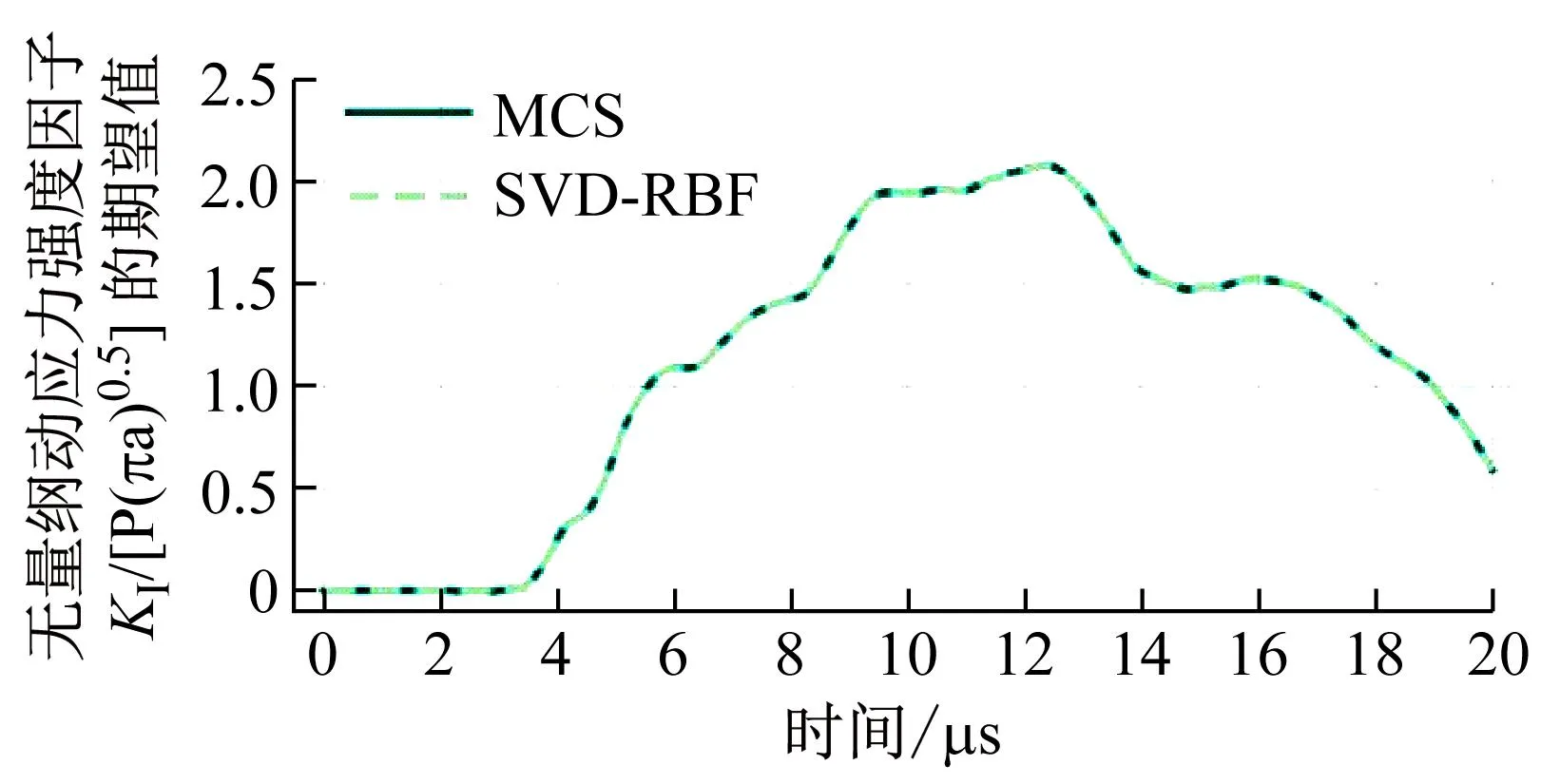
图10 无量纲动应力强度因子KI的统计特征

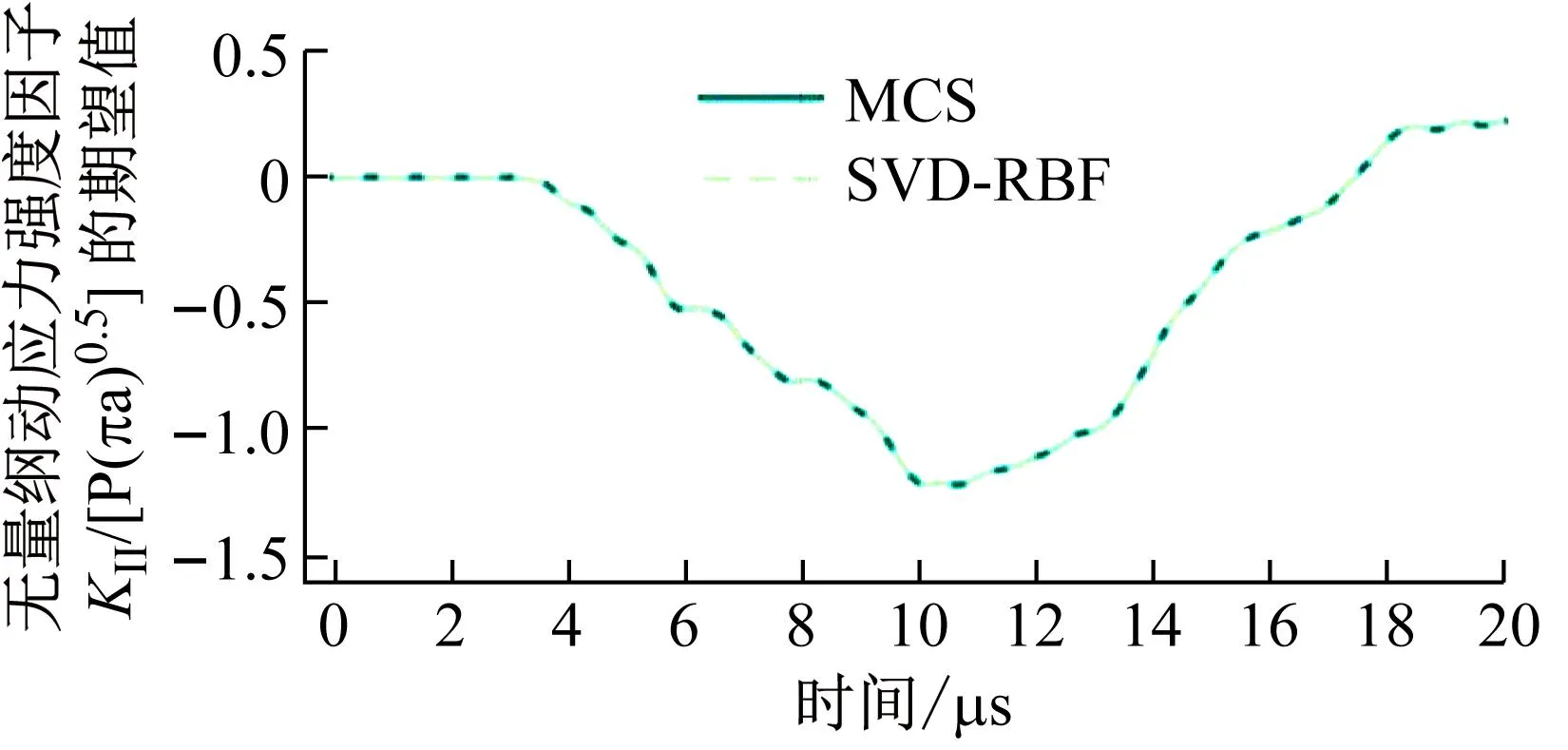
图11 无量纲动应力强度因子KII的统计特征

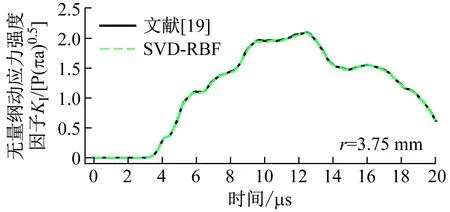
图12 本文算法解与参考解的动应力强度因子对比

3.4 带有裂纹的重力坝-地基系统的地震响应分析

本节研究岩石地基对大坝动力断裂的影响。大坝的几何尺寸如图13所示。大坝材料为混凝土,其力学参数为:弹性模量Ec=31.0 GPa,泊松比vc=0.15,密度ρc=2 643 kg/m3;下部是岩石地基,部分力学参数vr=0.25,ρr=2 643 kg/m3。依照文献[33],选取初始裂纹的高程为59.25 m,初始长度为1 m,输入的地震动为Koyna地震波。设定岩基的弹性模量为不确定性参数,其波动范围为[10～15],步长为0.1选取50个Er作为蒙特卡罗模拟的结果。整个计算采用平面应变假定。

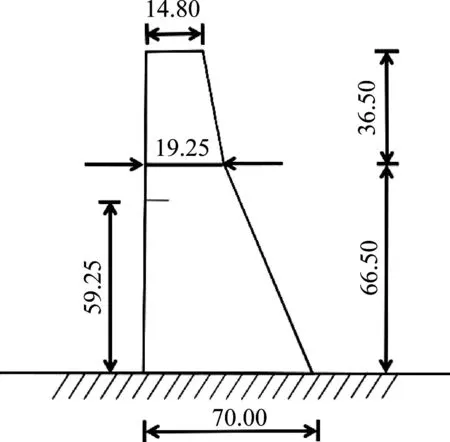
图13 Koyna大坝几何模型 (m)

采用多边形单元进行离散,划分93个多边形单元458节点,其网格如图14所示。其中截断边界采用11个三节点线单元离散,相似中心选取为坝基的中点处,采用基于连分式算法的高阶透射边界模拟坝基无限域。选取动态应力强度因子KI作为响应,计算时间为10 s,步长Δt=0.01 s。

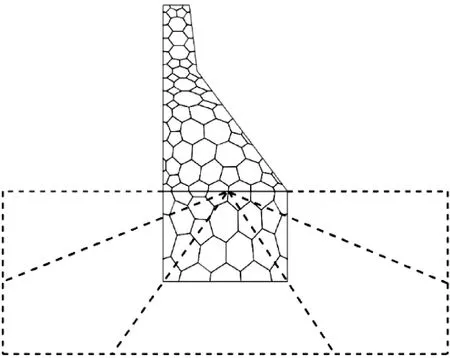
图14 SBFEM网格

图15给出了本文算法和直接蒙特卡罗模拟获得的统计特征的对比图。从图15可以看到,两种方法得到的统计特征基本一致。值得注意的是,算法只使用了11个初始样本点形成快照矩阵,且采用方案2的策略对快照矩阵进行降阶处理。大大节省了储存空间,提高了计算效率。为了进一步说明算法的准确性,图16给出了Er=12 GPa算法的结果,与已有文献结果[33]对比,这里的Er=12 GPa是算法预测得到结果而非初始样本点。从图16可以看出,算法解与参考解吻合得很好。KI的峰值发生在4 s处,在弹性模量Er的波动范围内,峰值处KI从8 641 527.9 Pa·m0.5波动到7 023 890.08 Pa·m0.5相对波动范围为18%,可见岩基参数的不确定性对动态应力强度因子有较大影响,因此研究不确定参数对结构响应的影响是很有意义的。

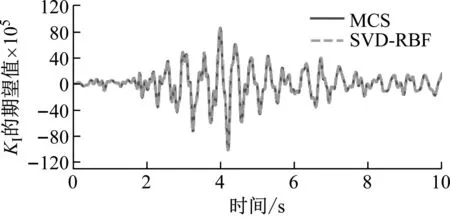
图15 归一化动应力强度因子KI的统计特征

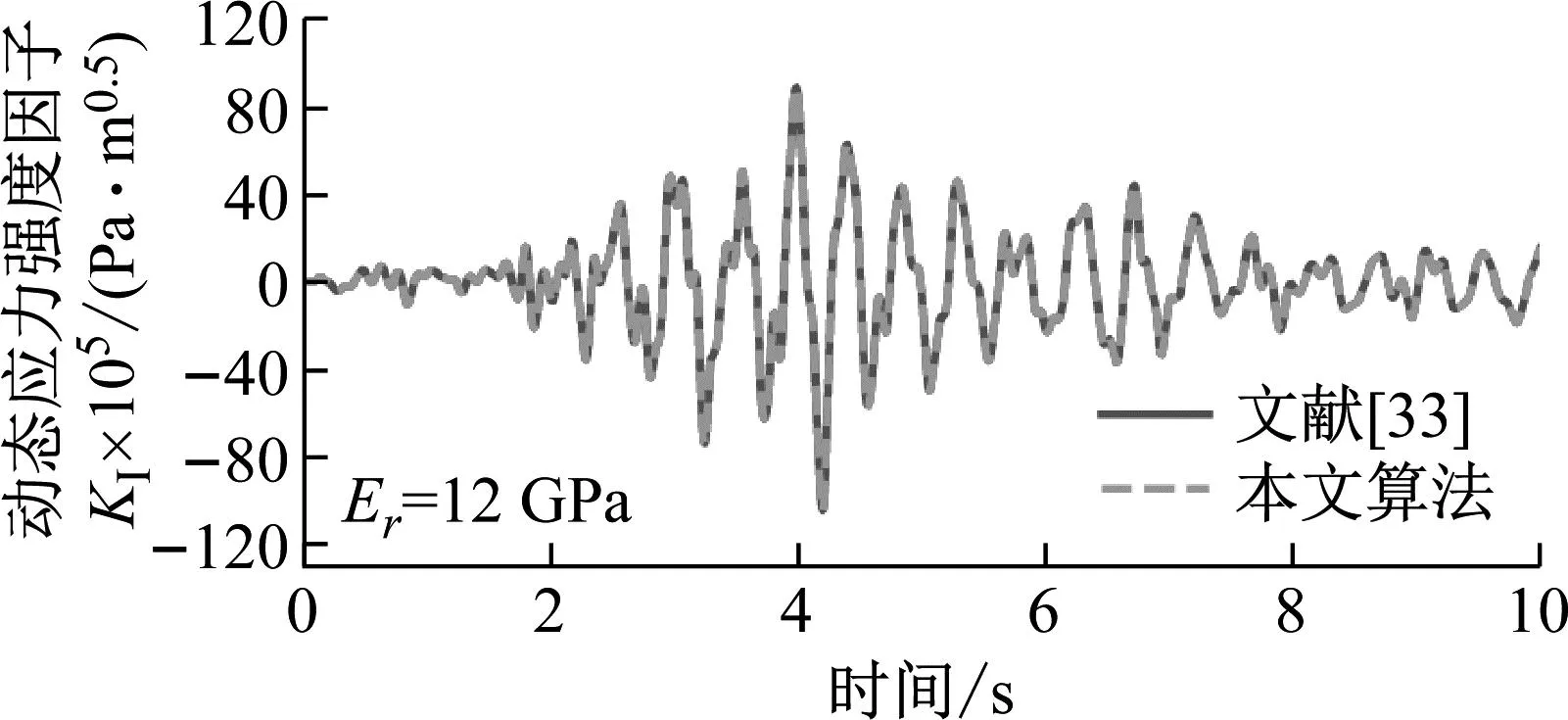
图16 Er=12 GPa时本文算法解与参考解的结果对比

4 结 论

本文构建了一种新的使用比例边界有限元法计算应力强度因子的蒙特卡罗模拟框架,并得到如下结论:

(1) 采用多边形比例边界有限元法分析断裂问题时,将比例中心设置在裂纹尖端,使裂纹尖端不需要网格细化,可直接提取应力强度因子,为不确定量化提供了高精度的计算模型。

(2) 采用蒙特卡罗模拟计算响应的统计特征,量化不确定参数对结构响应的影响,并使用模型降阶法对传统的蒙特卡罗模拟进行改进,直接降低物理问题的自由度,快速获得新的结构响应,并讨论了奇异值矩阵的合理截断。同时,考虑了不同变异系数对结构响应的影响,对大的变异系数(0.4)的结果也有较高的精度。

(3) 数值算例表明,对于不同的变量和不同的物理模型,使用SVD-RBF加速MCS具有良好的精度。

并且能显著降低计算成本,提升了传统蒙特卡罗模拟的适用性。