大型汽轮发电机定子端部绕组物理参数识别及数学模型建立方法研究

赵 洋,刘晋珲,肖 洋,邓聪颖,马 莹

(1.重庆邮电大学 先进制造工程学院,重庆 400065; 2.重庆邮电大学 高等科学研究院,重庆 400065;3.西安交通大学 机械结构强度与振动国家重点实验室,西安 710049)

近年来,随着电能需求的急剧增加,大型汽轮发电机的最大容量已提升至上千兆瓦,导致其定子端部绕组的振动问题日益严重。对于二极汽轮发电机,当端部绕组固有频率接近100 Hz时,可能会发生共振现象。此外,随着发电机组的运行,定子端部的连接紧固件可能出现连接松动,这将导致端部整体结构的质量和刚度发生改变,端部的固有频率会随之变化。以上情况都对大型汽轮发电机的安全运行造成威胁,因此深入掌握定子端部绕组的动力学性能至关重要。

国内外大量学者针对发电机定子端部绕组振动问题开展了大量的理论与试验研究,取得了显著成果。推导出端部绕组在不同工况下的磁场分布和电磁力的表达式[1-2],并建立了端部绕组的简化振动分析模型,得到了电磁力作用下的振动响应[3-5]。王益轩等[6-9]则通过对线棒、压板等主要构件进行近似建模,建立简化的端部绕组有限元模型研究其动力特性,并考虑了不同结构参数变化对端部绕组固有频率的影响规律;Iga等[10]建立了一种将线棒等效处理为复合材料的端部绕组精细化模型,并将该模型用于分析定子端部绕组的固有频率。赵洋等[11-12]在前期工作中建立了600 MW汽轮发电机端部绕组的精细有限元模型,并研究了端部结构在电磁力作用下的变形和应力响应,最后通过参数化研究提出了端部绕组的优化方案。陈力飞等[13]通过灵敏度计算分析了1 200 MW汽轮发电机定子绕组端部各结构的材料参数和几何参数对端部固有频率的影响。杨昔科等[14-15]沿用有限元方法建立数字化模型研究不同型号电机端部绕组的动力特性,其仿真计算结果与试验结果一致。Hu等[16]根据有限元等效模型和模态试验得到的模态参数推导出线棒的等效正交各向异性的材料参数。Lange等[17-18]对线棒的铜芯和绝缘层采用单独的材料模型,从而建立端部绕组的有限元模型,并基于此模型研究了温度对定子端部振动的影响。近期,Zhao等[19]采用近似模型方法研究端部绕组的典型固有频率值预测方法。

综上,学者们针对定子端部绕组的动力特性主要研究思路包括:①建立端部绕组的有限元模型,采用计算模态方法评估动力特性;②针对样机进行离线试验模态分析,得到端部绕组的模态参数。暂未查阅到对端部绕组的物理参数展开深入研究的相关内容。

结构的物理参数不仅是评估损伤和可靠性的直接应用参数,也是构建数学模型的必要元素。因此本文基于结构的频响函数,提出一种利用最小二乘复频域法识别模态参数,再由模态参数修正集中质量法获取的物理参数,从而建立结构数学模型的方法。该方法不仅能够准确地反映端部绕组的动力学特性,同时可指导后续端部绕组进行结构优化和损伤鉴别。本文研究方法流程图如图1所示。

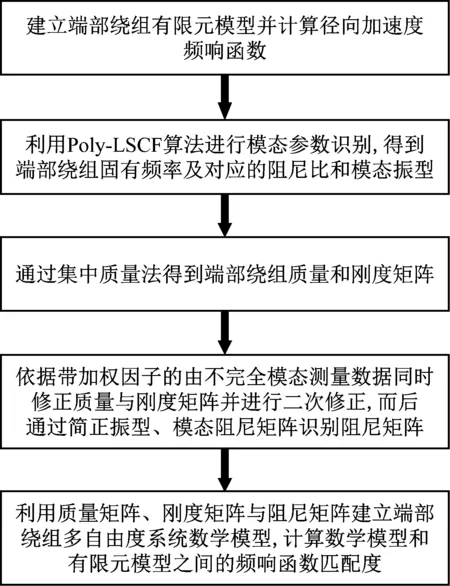
图1 研究方法思路流程图

1 最小二乘复频域法识别模态参数

1.1 极点和留数估计

对于一个多输入多输出系统(multi-input multi-output,MIMO),输入量为Ni,输出量为No。频响函数的第o行(o=1,2,…,No)可以表示为

Ho(ω)=Bo(ω)A-1(ω)

(1)

式中:Ho(ω)为频响函数的一行;A(ω)为分母矩阵;Bo(ω)为分子矩阵;Bor、Ar分别为待估计参数;n为系统拟合计算阶次;Ωr(ω)为基函数。其表达式如下

Ωr(ω)=e-ωΔt×rj,ω=2π(f-fmin),

(2)

式中:Δt为识别频段的频率分辨率;f为离散频率。

利用最小二乘法求解拟合的频响函数与测量的频响函数之间误差最小时,可得到如下方程

(3)

式中:J为雅可比矩阵;JH是J的共轭转置矩阵;θ、βo、α、Ro、So、To均为参数变量,有如下定义

Yo=

(4)

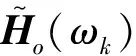
将式(3)中前No行得到的βo代入式(3)中最后一行得到缩减的正则方程M[20]

(5)

同时将分母系数最高项An限制为单位矩阵,得到分母系数α的解为

α=

(6)

当分母系数求解完成之后,对伴随矩阵AC进行特征解可得

(7)

极点λi=e-pi·Δt在Λ的对角线上,便可得到相应的固有频率与阻尼比;模态参与因子γ对应于V的最后Ni行。振型则可通过以下公式估计

(8)

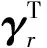
(9)

式中:s为拉普拉斯变量;Ar为频响函数的留数。

1.2 模态振型求解

在试验模态分析中,依据留数可得到系统的模态振型。留数在第r阶模态展开时

(10)

留数大小可以通过拟合测得的频响函数得到,当有驱动点的数据时

(11)

式中:aiir为留数矩阵元素;uir、ujr为振型元素。

以模态质量归一化法为例,其中mr=1可以得到以下关系

(12)

从式(12)可以得出:对于实模态,留数为纯虚数,并且驱动点的留数虚部是非正数。

(13)

为保证此解满足留数的基本特性,对等式设置两个约束条件:第一个约束条件是留数为纯虚数;第二个约束条件是驱动点的留数虚部是非正数。

将上述两个约束条件代入频响函数进行求解,具体的求解过程如下

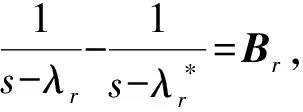
(14)

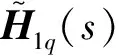
(15)

接下来再根据差值进行高低阶残余项的求解

(16)

2 物理参数识别及数学模型建立

2.1 集中质量法离散结构

实际的工程结构大多数为连续系统,通常可用集中质量法近似为多自由度系统。如图2(a)所示,对于固支梁结构可分成8段,将其离散为7自由度系统。根据质量影响系数和柔度影响系数便可得到离散后系统的质量和刚度矩阵。同理,对于端部绕组结构,可将其近似简化为圆锥壳结构[21],可沿径向方向平分成n等份梯形块,再将每一块的质量均分到4个节点上,若小径端被固定且仅考虑大径端的径向振动,那么圆锥壳便可离散成n自由度系统,其离散及力学模型简图如图2(b)所示。

(a) 固支梁

2.2 根据模态参数修正物理参数及数学模型建立

采用集中质量法计算得到结构质量和刚度矩阵可能会产生较大的误差。本文利用文献[22-23]中提出的一种带加权因子的由不完全模态测量数据同时修正质量矩阵与刚度矩阵的方法。

该修正方法中将集中质量法获取的质量矩阵Ma、刚度矩阵Ka以及模态参数识别的固有频率平方矩阵Ω2、模态振型Φ作为输入数据,对Φ进行QR(正交三角)分解,得到:

(17)

式中:Q=[Q1Q2];R为非奇异矩阵。

接着计算Ma11、Ma12、Ka11、Ka12和矩阵Z,即:

Z=R-TΩ2RT

(18)

考虑到质量矩阵的数量级远小于刚度矩阵的数量级,选取一个较小的加权因子μ后计算ΔM12得到

ΔM12=(IS+μZTZ)-1(Ma12+μZTKa12)-Ma12

(19)

通过计算ΔMOPT和ΔKOPT得到第一次修正后的M=Ma+ΔMOPT、K=Ka+ΔKOPT,其中ΔMOPT和ΔKOPT的计算公式如下

ΔKOPT=

(20)

上述计算流程已经获取了修正后的质量和刚度矩阵,而阻尼矩阵则由模态阻尼矩阵与振型之间的关系计算得到。对矩阵M-1×K进行特征值分解后可以得到修正后的简正振型ΦN,模态阻尼矩阵Cq和阻尼矩阵C分别为

Cq=diag(2ω1ξ1,2ω2ξ2,…,2ωnξn)

(21)

利用得到的质量矩阵、刚度矩阵和阻尼矩阵建立多自由度系统的数学模型。通过求解该数学模型获取发电机定子端部绕组的频响函数,将发电机定子端部绕组所受外力作为该数学模型的输入,可预测待测结构的响应,该数学模型表示为

(Ms2+Cs+K)X(s)=F(s)

(22)

由于仅考虑结构振动的实模态,因此将C设为对角阵。此时,各个矩阵满足正交条件

ΦTMΦ=diag(mi)

ΦTKΦ=diag(ki)

ΦTCΦ=diag(ci)

(23)

式中,mi、ki、ci分别为模态质量、模态刚度和模态阻尼系数。

为了验证识别的物理参数和数学模型的准确性,将数学模型求解得出的频响函数与测试的频响函数进行对比验证,采用如下的匹配度进行评判

(24)

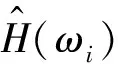
3 方法的可行性分析

建立与图3(a)中所示的固支梁对应的有限元模型,其中梁的参数:杨氏模量E=2.1×1011Pa,密度ρ=7 850 kg/m3,长度l=0.75 m,截面为矩形,宽度a=0.04 m,厚度t=0.004 m。采用有限元软件ABAQUS对其进行模态分析并与图3(b)中的锤击试验进行对比验证模型的准确性。进一步对固支梁进行谐响应分析,设置全局阻尼为0.02。对测点3施加单位正弦力F进行y方向激励,扫频范围为20～250 Hz,得到各测点y方向的加速度响应,如图4所示。

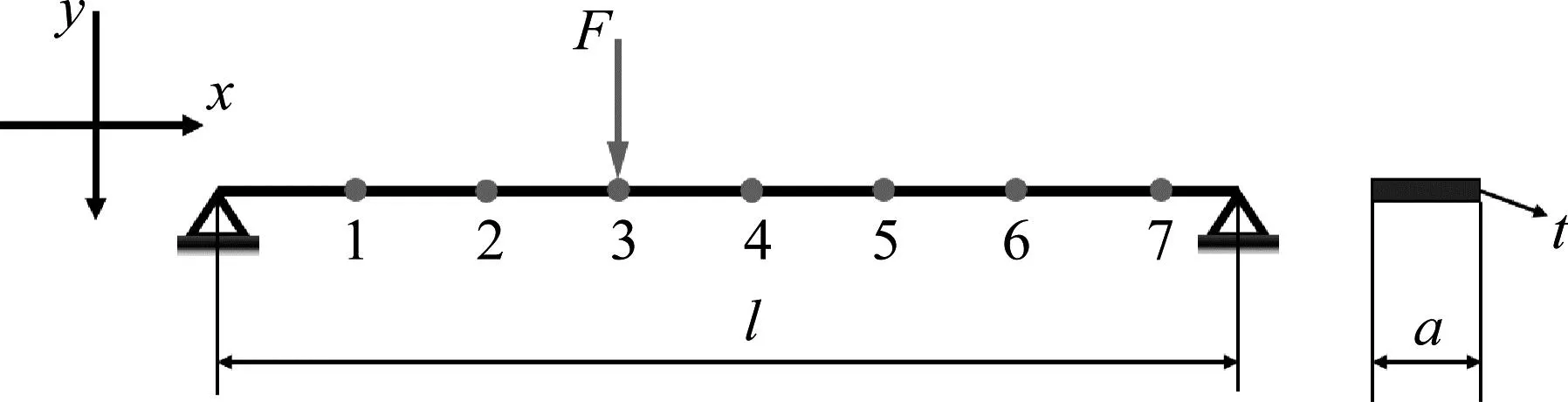
(a) 仿真试验示意图

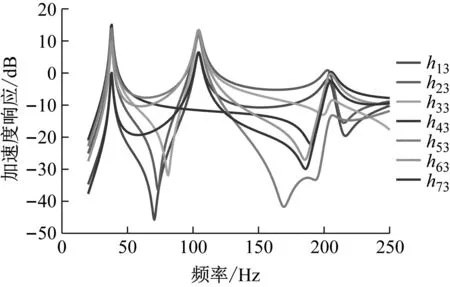
图4 固支梁测点1～7加速度频响函数

采用“单点激励多点响应”方法(SIMO),利用最小二乘复频域法对固支梁hi3的加速度频响函数识别的稳态图结果如图5所示,其中标示点‘s’表示该极点为稳定极点。将识别出的固有频率和阻尼比与有限元结果进行对比,如表1所示。可见,固支梁的固有频率和阻尼比的识别结果与有限元计算结果十分接近,仅固有频率存在误差,最大误差为0.03%。

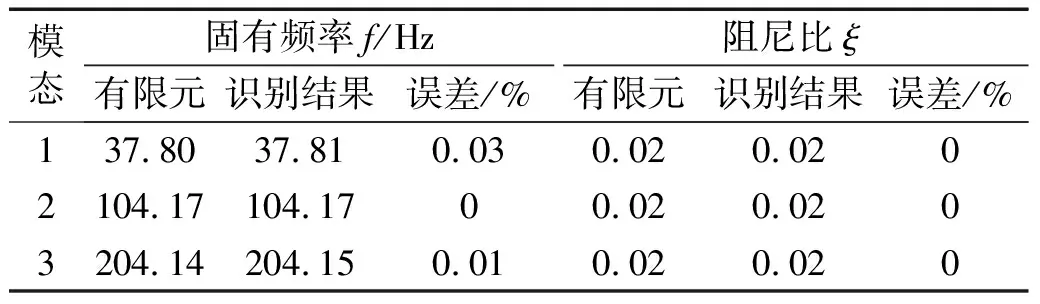
表1 固支梁识别的固有频率和阻尼比与有限元结果对比

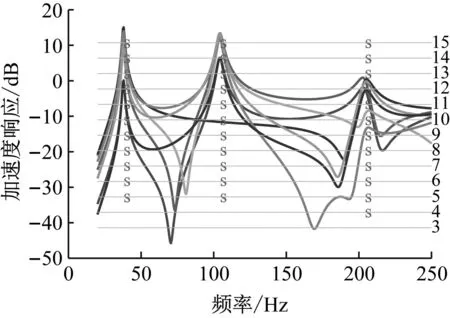
图5 固支梁hi3加速度频响函数识别情况

进一步将识别的振型与有限元计算的振型进行对比,如图6所示。结果显示,识别出的模态振型与有限元振型一致。

(a) 第1阶模态(f=37.80 Hz)

采用集中质量法将固支梁离散成7自由度系统。利用质量影响系数,得到质量矩阵如下

同样地,利用柔度影响系数,得到刚度矩阵为

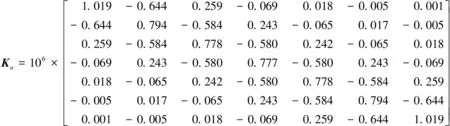
利用集中质量法计算得到固支梁的固有频率与有限元计算的固有频率对比如表2所示。可以看出,固有频率的阶数愈高计算误差愈大。整体来看,由于固支梁结构简单,利用集中质量法能够获取较高精度的模态参数,但仍可通过修正进一步提高精度,该方法应用于复杂结构时效果更加明显。

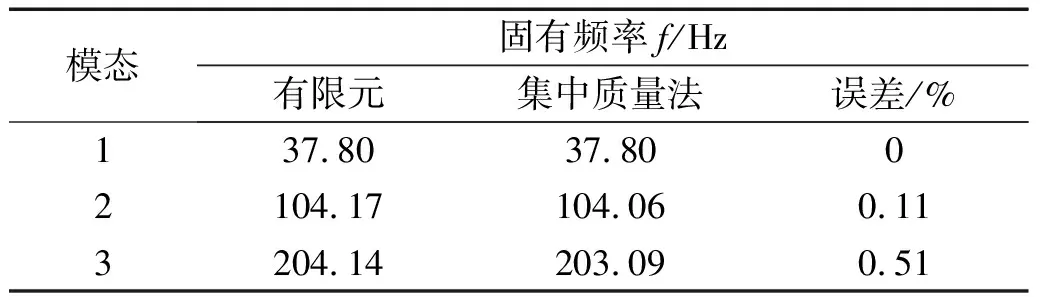
表2 固支梁集中质量法计算的固有频率和有限元结果对比

基于固支梁模态参数,选用加权因子μ=1×10-6,通过修正后可得质量、刚度和阻尼矩阵分别为

修正后,质量矩阵非对角线上的元素不全为0,这说明原模型存在惯性耦合。根据修正后的矩阵建立固支梁的数学模型,重新计算固支梁的固有频率,与有限元结果对比如表3所示。图7是修正物理参数后的数学模型所得到测点1～7的位移频响函数与原位移频响函数的对比结果,匹配度均达到了99%。

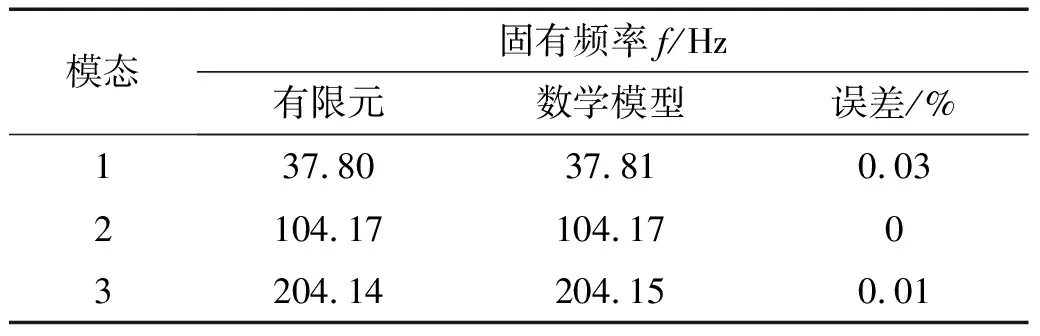
表3 固支梁数学模型计算的固有频率和有限元结果对比

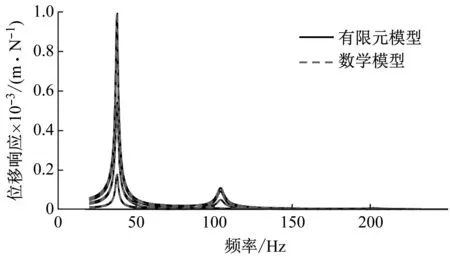
图7 固支梁数学模型计算的位移频响函数和有限元结果对比图

通过表3和图7可见,数学模型计算得到的固有频率和频响函数均与有限元模型结果高度一致。可知修正后的物理参数合理可靠,且数学模型能准确反映固支梁在20～250 Hz频率段中的动力学性能,证明了本文提出方法的可行性。

4 定子端部绕组物理参数识别及数学模型建立

笔者前期已经建立600 MW汽轮发电机定子端部绕组有限元模型,其边界条件及单元划分如图8所示。通过ABAQUS进行模态分析,同时为了验证模型的准确性也在相同机型出厂时进行了锤击试验。试验采用PCB公司锤击力锤和加速度传感器,多点激励单点响应并用南京安正模态分析软件进行分析,现场如图9所示。将求解的端部绕组各阶模态与实测结果进行对比,如图10所示。

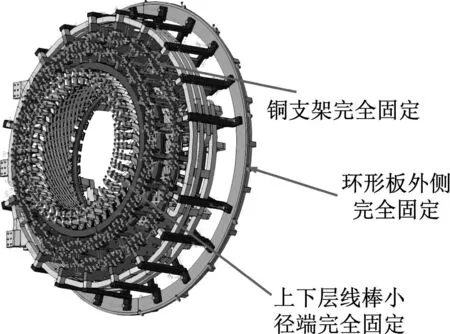
(a) 边界条件

图9 样机模态试验实测现场

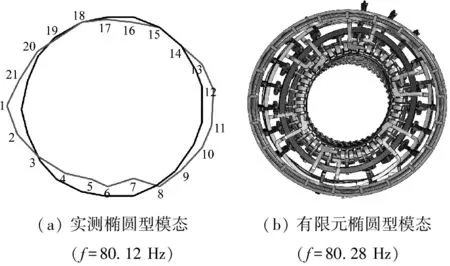
图10 定子端部绕组有限元模态振型与实测振型对比图

由图10可见,ABAQUS计算的端部绕组的固有频率与实测的固有频率十分接近;由于实测传感器数量及噪声问题,两者得到的振型存在细微差别,能够证明有限元模型的合理性、可靠性。

在提取结构的频响函数时,由于端部绕组具有对称性,且本研究主要关注其径向振动,所以在端部绕组半圆周的鼻端处布置11个测点,如图11所示。

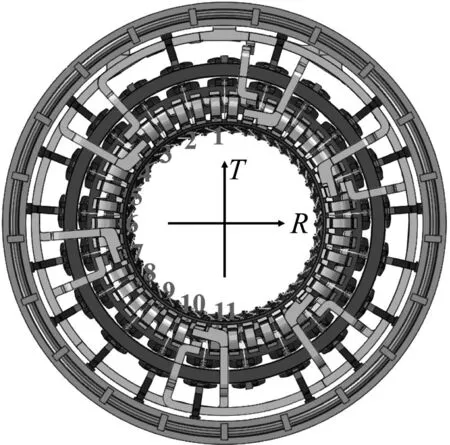
图11 整体绕组的测点布置

在测点1施加沿径向的正弦单位力进行激励,输出测点1～11的径向加速度响应,扫频范围为75～115 Hz,得到各测点的频响函数hi1(i=1,2,…,11)如图12所示,各频响函数用于后续模态参数识别。

图12 定子端部绕组测点1～11加速度频响函数

对端部整体绕组的hi1径向加速度频响函数进行识别,识别结果如图13所示。

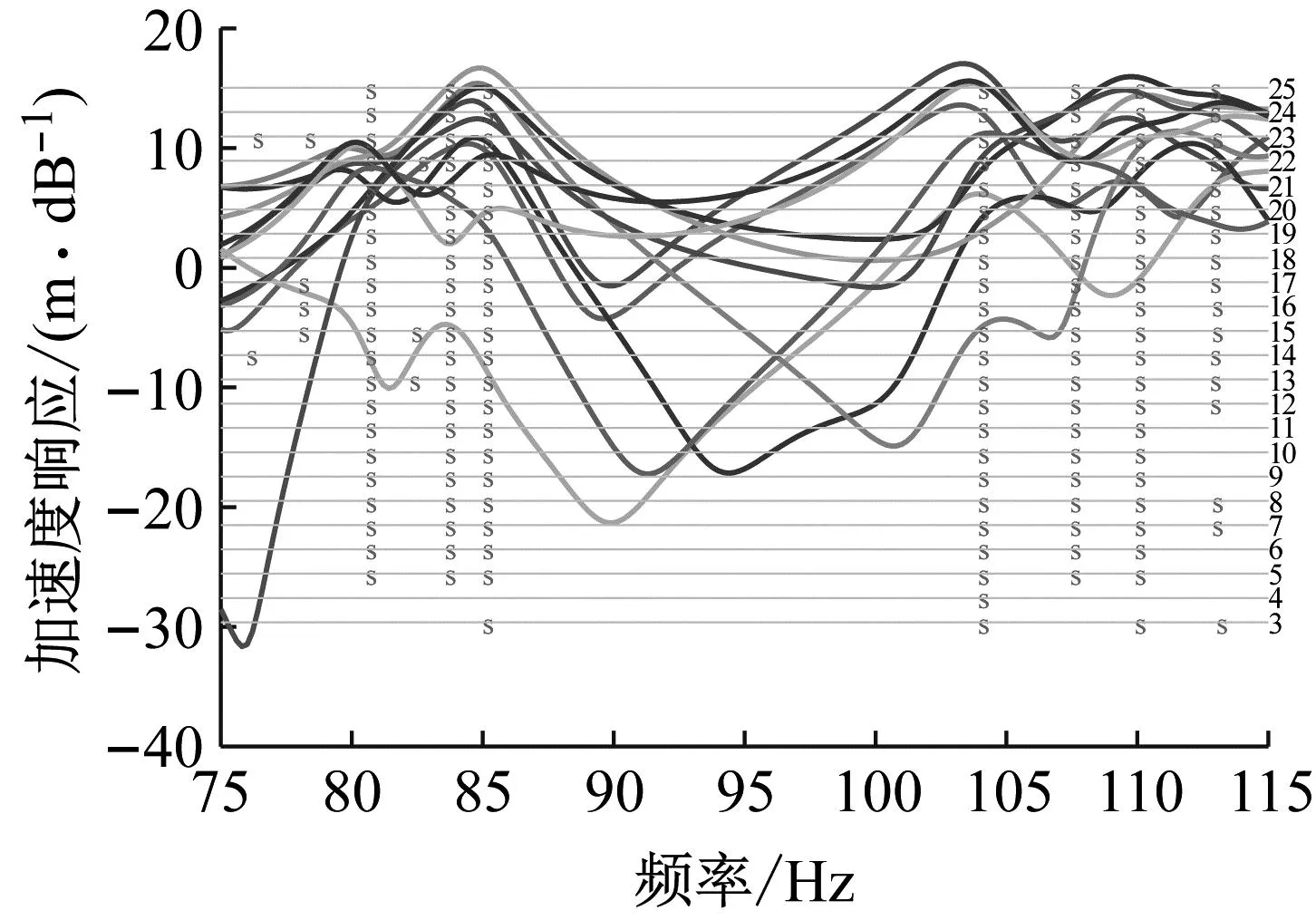
图13 整体绕组hi1的径向加速度响应识别情况

识别出的各阶模态的相应的振型对比如图14所示。固有频率和阻尼比与有限元结果的对比结果示如表4所示。由图14和表4可知,识别出的固有频率、阻尼比以及模态振型与有限元计算结果均一致,其中固有频率和阻尼比的最大误差出现第1阶模态中,分别为0.27%和0.50%,再次证明模态参数识别方法的准确性。

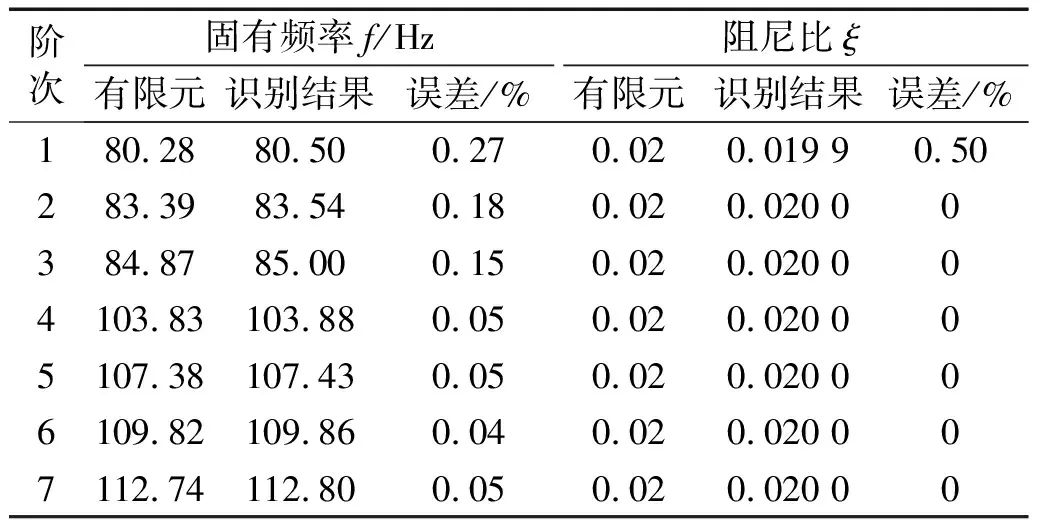
表4 端部绕组识别的固有频率和阻尼比与有限元结果对比

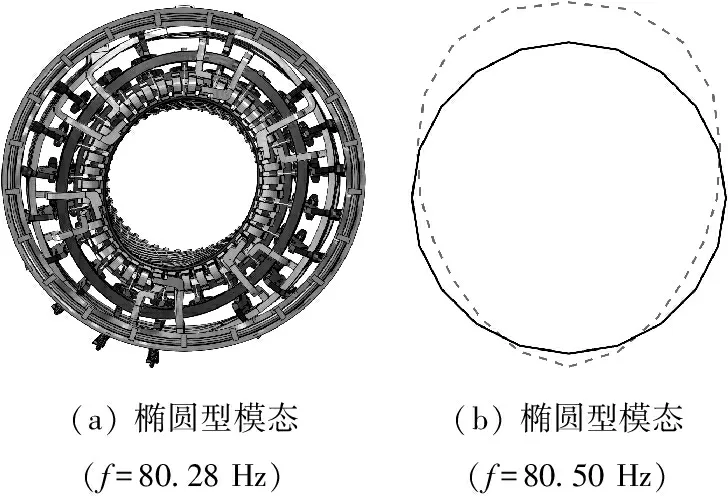
图14 端部绕组有限元振型与模态识别振型对比图

为了进行更深入的研究,根据集中质量法将端部绕组离散成11个测量自由度的多自由度系统,其离散过程与2.1节中圆锥壳的离散过程一致。利用质量影响系数法获得质量矩阵,结合图11中的有限元模型获取柔度矩阵。在模型中的1号节点上施加单位力,提取其余各个节点上的位移值就得到了相应的柔度系数fi1,重复上述操作可得到全部柔度系数,根据刚度矩阵与柔度矩阵的互逆性,便可得到系统简化的初始刚度矩阵。端部绕组系统的质量矩阵和刚度矩阵分别如下

将集中质量法计算得到的定子端部绕组三个典型模态的固有频率及其对应的振型与有限元结果进行对比,如表5所示。结果显示,只有椭圆型模态对应的固有频率误差相对较小,为4.45%;而对于三瓣型模态,集中质量法计算的结果均小于有限元结果,且误差已接近20%;同时模态振型也存在较大差异。这是由于质量的集中方式和刚度等效代换的随意性导致的。

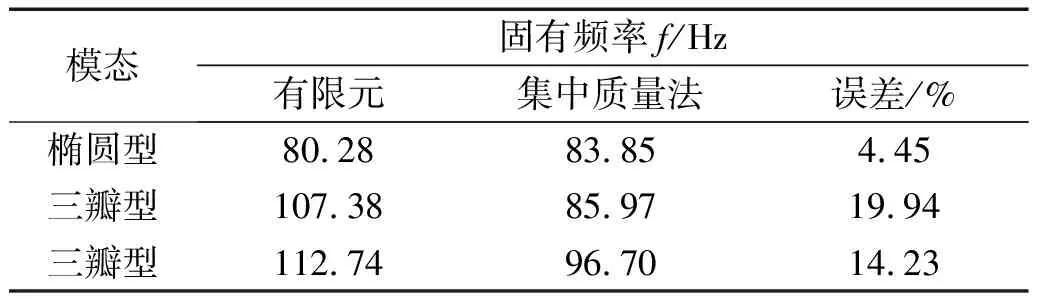
表5 端部绕组集中质量法计算的固有频率与有限元结果对比

接下来,基于2.2节中的方法,利用75～115 Hz频率段中识别出的模态参数对质量集中法的质量和刚度矩阵进行修正。

得到修正后的质量矩阵、刚度矩阵以及阻尼矩阵分别如下

最后利用修正后的物理参数建立端部绕组的数学模型,将数学模型计算得到的三个典型模态的固有频率及其对应的振型与有限元结果进行对比,如表6和图15所示。此外,使用数学模型计算出端部绕组的径向位移频响函数,测点1作为激励输入点,激励为单位正弦力,输出测点1、4、6、8、11的位移响应,与有限元计算的频响函数对比如图16所示,受结构模态振型影响各频响函数峰值并不一致,相应的频响函数匹配度如表7所示。

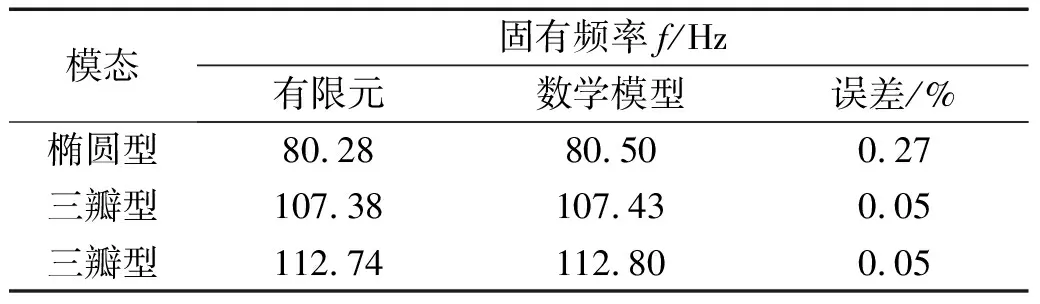
表6 端部绕组数学模型计算的固有频率与有限元结果对比

表7 端部绕组数学模型计算的位移频响函数和有限元结果匹配度

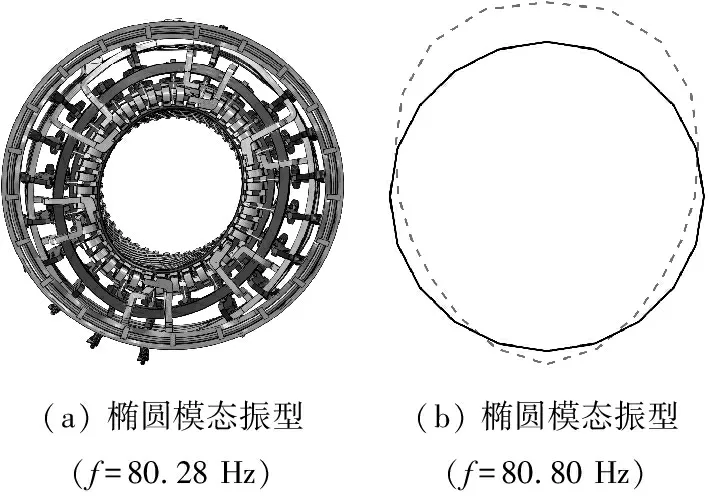
图15 整体绕组数学模型计算的模态振型与有限元结果对比图

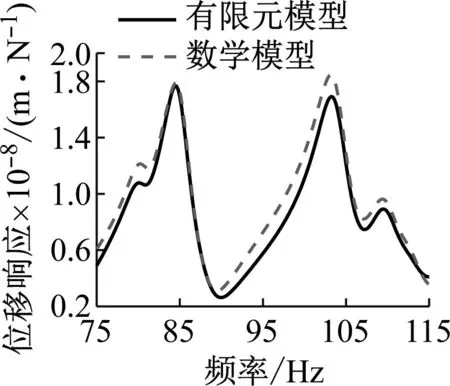
(a) h11径向位移响应

由图16和表7可知:修正后建立的数学模型和有限元模型计算的固有频率最大误差仅为0.27%,两者振型一致;两者计算的频响函数在高阶截断处误差稍大,固有频率附近的频响函数误差较小,其中测点4的匹配度最小为76%,测点8具有最高匹配度为95%,多数测点的匹配度达到85%以上,能满足实际工程需求。上述内容可证明本文识别出的端部绕组物理参数准确性以及建立的数学模型能够准确反映定子端部绕组在75～115 Hz频率段中的动力特性。

5 结 论

本文基于结构的频响函数,提出利用最小二乘复频域法识别模态参数,进一步用模态参数修正由集中质量法获取的物理参数,最后根据物理参数建立符合结构响应的数学模型的方法。

(1) 在简支梁模型上验证了该方法的可行性,结果显示修正后的数学模型能够准确描述结构的动力学特性。

(2) 对600 MW汽轮发电机端部绕组精细数字化模型进行频响函数提取,从中识别出的模态参数与有限元结果十分接近,固有频率和阻尼比的最大误差均在第1阶模态,分别为0.27%和0.50%。

(3) 完成端部绕组的物理参数识别并建立其数学模型,将数学模型得到的频响函数与有限元结果进行对比,多数测点的匹配度达到85%,最大可达95%。

本文提出的识别物理参数和建立数学模型的方法可为端部绕组动力学问题研究提供准确的建模与参数评估依据,为其安全运行和优化设计奠定理论基础。