基于多尺度形态滤波和递归求差的冲击特征自适应分离方法
和 丹,权 伟,汤明军,刘 晖
(1.西安工程大学 机电工程学院,西安 710048; 2.西安市现代智能纺织装备重点实验室,西安 710600;3.西安交通大学 机械工程学院,西安 710049)
周期性冲击特征提取和辨识是旋转机械故障诊断中的关键环节。但在实际工业现场,由于振动传输路径和多振动源耦合等因素影响,测得的振动信号中不仅包含与故障相关的弱周期性冲击,还包含信号传递中强背景噪声[1]。因此,从复杂振动信号中准确提取和分离出周期性冲击特征对机械设备故障诊断具有极其重要的意义。
针对周期性冲击特征提取和分离,国内外研究者开展了大量研究工作,可分为三类:第一类是利用周期和冲击特性,结合数字滤波理论构造相应滤波器。如:最大相关峭度解卷积(maximum correlation kurtosis deconvolution,MCKD)[2]、多点最优最小熵解卷积(multipoint optimal minimum entropy deconvolution,MOMEDA)[3]、最大二阶循环平稳盲解卷积(maximum second order cyclostationary blind deconvolution,CYCBD)[4]和谱峭度[5]等。这类方法通常能够最大程度强化冲击特征,但容易受随机冲击干扰影响,且在复合故障诊断时需要设计多个滤波器进行,适合使用场景为无随机冲击干扰影响,共振带和故障频率未知的故障冲击识别[6]。第二类是利用周期性冲击波形特征和内积理论设计相应滤波器,如:匹配追踪[7],拉布拉斯小波[8]等。这类方法通常需要设计与故障匹配的原子库,且计算量大,优点是能最大限度还原故障信号,适合故障特征已经情况下的故障信号提取[9]。第三类是利用通用型分解方法开展冲击特征提取研究。如:经验模态分解(empirical mode decomposition,EMD)[10]、局域均值分解(local mean decomposition,LMD)[11]、变分模态分解(variational modal decomposition,VMD)[12]等。该类方法可将冲击特征分解到多个模式分量,通常需要结合其他指标进一步筛选故障特征,优点是不限于冲击特征分离,适合故障未知及多种故障类型的故障信号分离[13]。上述方法虽然在故障冲击特征提取中取得一定效果,但适用范围不尽相同。
形态滤波是一种非线性滤波方法,因其具有较强的非线性信号处理和信号形态细节特征保持能力成为故障诊断中研究热点。该方法利用结构元素对信号进行滤波,在保留特征信息的同时消除噪声成分,其效果主要依赖结构元素类型,结构元素尺度和形态学算子等。近些年研究主要关注如何自适应选择最优结构元素以及如何设计与结构元素匹配的形态学算子两方面。Li等[14]针对结构元素尺度对形态滤波结果不确定性问题,依据冲击信号特征,构造自适应结构元素,试验结果表明自适应结构元素较直线型,三角形元素在特征提取和计算效率方面效果更优。Chen等[15]为了提高形态滤波算法计算性能,将具有消除噪声的对角切片谱(diagonal slice spectrum,DSS)算法与形态滤波器结合,有效提升了特征提取能力。Duan等[16]针对随机冲击干扰下的弱冲击特征提取问题,将形态学滤波融入最小熵解卷积方法(minimum entropy deconvolution,MED)方法,成功消除路径中随机冲击干扰,准确提取出微弱故障特征。Wang等[17]为了提高形态滤波算法性能,利用多尺度思想构造多尺度增强最优梯度积滤波(enhanced optimal gradient product filter,EOGPF)器,并结合特征频率强度系数(characteristic frequency intensity coefficient,CFIC)指标实现了最优功率谱的选取。Guo等[18]为了提高形态滤波算法计算性能,利用迭代思想设计一种迭代形态差分积小波流程,有效提高了故障诊断精度。上述研究虽然在微弱冲击特征提取和抗随机冲击干扰方面取得一定成果,然而多故障耦合中周期性冲击特征的准确提取和分离并未完全解决。
考虑到形态学滤波具有较好的泛化能力,本文将开展基于多尺度形态学滤波的冲击特征自适应提取和分离技术研究,旨在实现弱故障提取和复合故障分离。首先,筛选适合冲击特征分离的形态学滤波算子,并分析其滤波特性;然后,利用形态学算子、加权谐噪比、SOSO(strengthen operate subtract operate)特征增强理论和迭代求差思想构造一种多尺度故障特征提取和分离方法;最后,利用仿真和试验信号验证该方法有效性。对比CYCBD和谱峭度方法,本文所提出的方法无需预设参数,且不受随机冲击影响,不仅对单一弱冲击提取有效,而且可以实现复合冲击有效分离。
1 基本原理
1.1 形态学滤波
形态学滤波由于其计算效率高并能处理非线性信号,被广泛应用于旋转机械的故障诊断上。基本的形态学算子是由腐蚀、膨胀、开、闭算子组成。假设原始信号f(n)是一维离散信号定义为F=(0,1,…,N-1),g(m)也是一维离散信号定义为G=(0,1,…,M-1),且(N≥M),g(m)是结构元素,则数学形态学的四种基本运算定义如下:
膨胀算子 (f⊕g)(n)=max{f(n-m)+g(m)}
{1≤n≤N;1≤m≤M}
(1)
腐蚀算子 (fΘg)(n)=min{f(n+m)-g(m)}
{1≤n≤N;1≤m≤M}
(2)
开运算 (f∘g)(n)=(fΘg⊕g)(n)
(3)
闭运算 (f·g)(n)=(f⊕gΘg)(n)
(4)
式中,⊕Θ∘·分别表示膨胀、腐蚀、开、闭运算。
通过四种基本的形态学算子的级联组合可以构造出复杂的组合形态学算子,如下:
开闭算子FOC=(f∘g·g)(n)
(5)
闭开算子FCO=(f·g∘g)(n)
(6)
闭-膨胀算子FCD=(f·g⊕g)(n)
(7)
膨胀-闭算子FDC=(f⊕g·g)(n)
(8)
腐蚀-开算子FEO=(fΘg∘g)(n)
(9)
开-腐蚀算子FOE=(f∘gΘg)(n)
(10)
形态梯度算子(morphological gradient,MG)
MG=(f⊕g)(n)-(fΘg)(n)
(11)
形态差分算子(difference filter,DIF)
DIF=(f·g)(n)-(f∘g)(n)
(12)
闭-开平均算子(average operator,AVG)
AVG=((f·g)(n)+(f∘g)(n))/2
(13)
平均组合差分算子(average combination difference,ACDIF)
ACDIF=(FCD(f(n))+FDC(f(n)))/2-
FEO(f(n))
(14)
组合形态滤波-帽变换算子(combination morphological filter-hat transform,CMFH)
CMFH=f(n)-(FCO(f(n))+FOC(f(n)))/2
(15)
1.2 CMFH特征分析
在四种基本形态学算子中,膨胀算子和闭运算能够保留信号的正脉冲,抑制负脉冲,相反,腐蚀算子和开运算保留负脉冲,移除正脉冲[19]。AVG为实现正负脉冲特征同步提取,将其进行级联组合得到FOC、FCO、FCD、FDC、FEO、FOE算子,但该类算子会导致信号产生偏移。为了解决偏移问题,前人又提出改进算子MG、DIF、AVG、ACDIF和CMFH[20]。
为筛选出最优冲击特征提取算子,利用本文仿真信号2、西储大学轴承外圈故障信号(#311,采样频率为12 kHz,损伤尺寸为0.014英寸,负载为2马力,转速为1 750 r/min)和渥太华轴承内圈故障信号[21](#I-A-1,采样频率为20 kHz,采样时长10 s,运行转速从12.5 Hz增加到27.8 Hz)分析形态学算子(AVG、ACDIF、DIF、MG、CMFH)冲击特征提取和分离特性。引入能量幅值(energy amplitude,EA)作为冲击特征提取能力评价标准,EA值越大,冲击特征提取能力越强。公式如下:
(16)
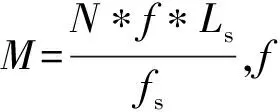
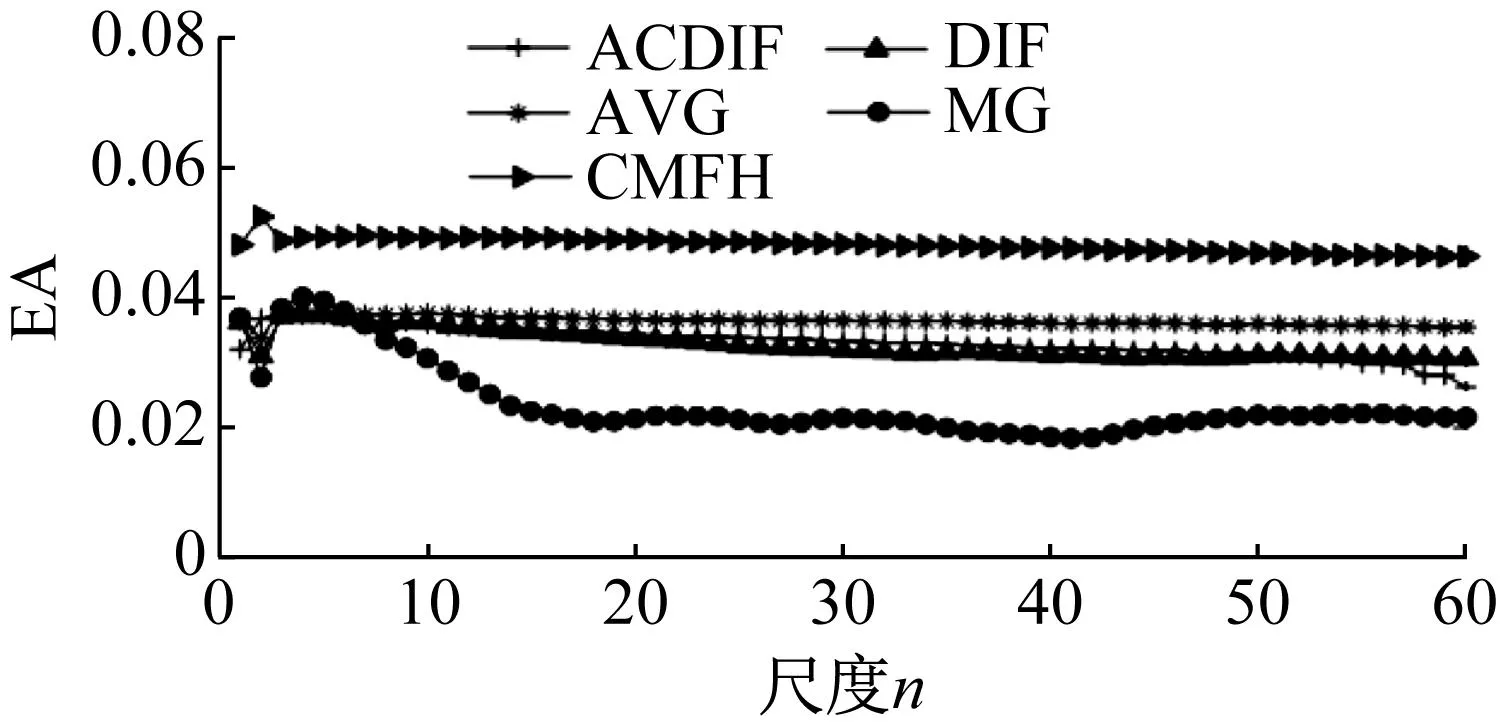
图1分别展示了三组不同信号下形态学算子(AVG、ACDIF、DIF、MG、CMFH)在尺度为1~60时EA值的变化情况,图1(a)、图1(b)和图1(c)中CMFH算子的EA值在各个尺度下都远大于其他算子,表明CMFH算子对冲击特征提取能力更佳。为掌握CMFH算子滤波特性,对其进行幅频响应分析,如图2所示。
(a)
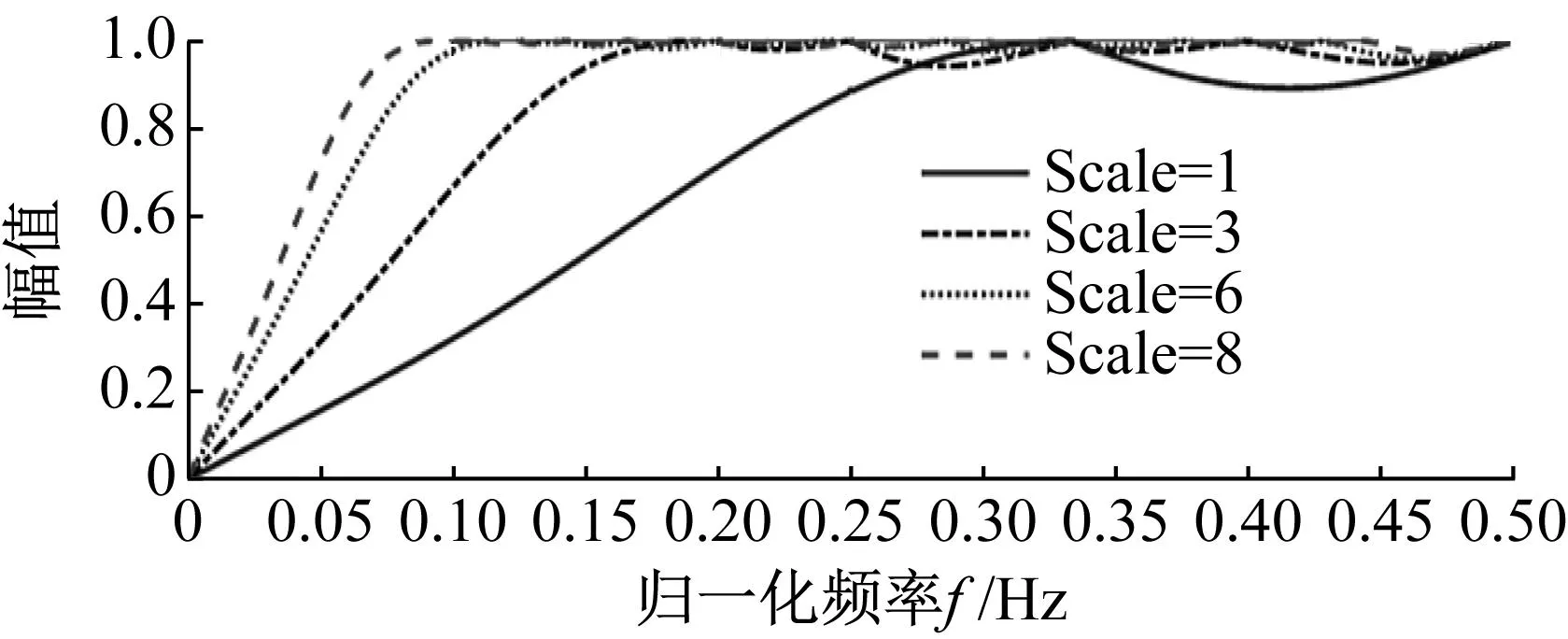
图2 CMFH幅频响应
从图2可以看出,随着尺度的减小,截止频率逐渐增大,即保留了更多的高频分量。这表明CMFH滤波器可以实现将故障特征按照尺度变化规律进行逐级分离。
1.3 SOSO增强技术
为了更大限度地提高故障信号中冲击特征强度,利用SOSO[22]增强技术提高整体算法去噪性能。具体流程,如图3所示。
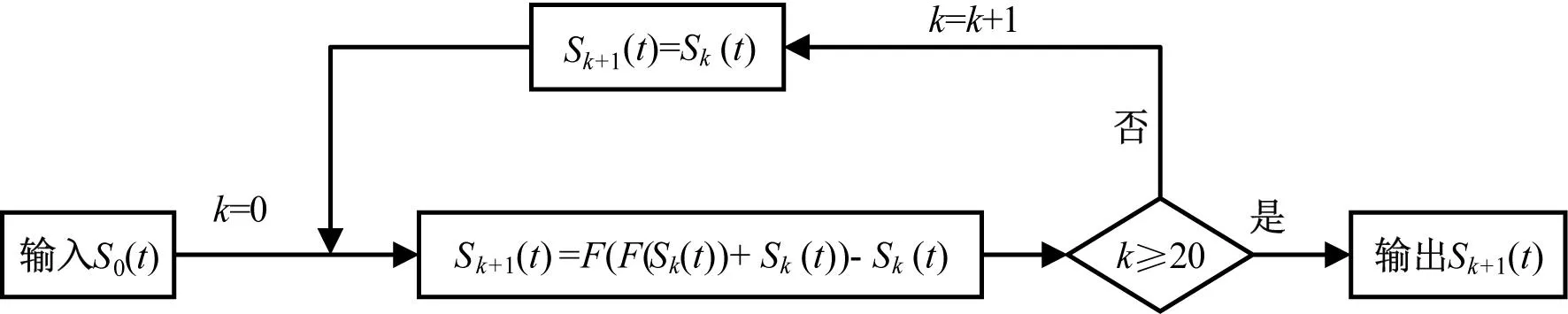
图3 SOSO强化信号特征流程图
图3中:Sk(t)为第k次滤波信号;S0(t)为测试信号,F(·)为滤波算法;k为循环滤波次数。上述增强算法可表示为SOSO(Sk(t))。在本文中,滤波算法采用多尺度形态滤波,k取20。具体见本文第2章流程图步骤1~3。
2 冲击特征自适应分离方法
本文结合多尺度形态滤波器、SOSO强化理论以及迭代求差思想提出了冲击信号分离法,可实现故障信号中冲击特征自适应分离和提取。流程如图4所示。
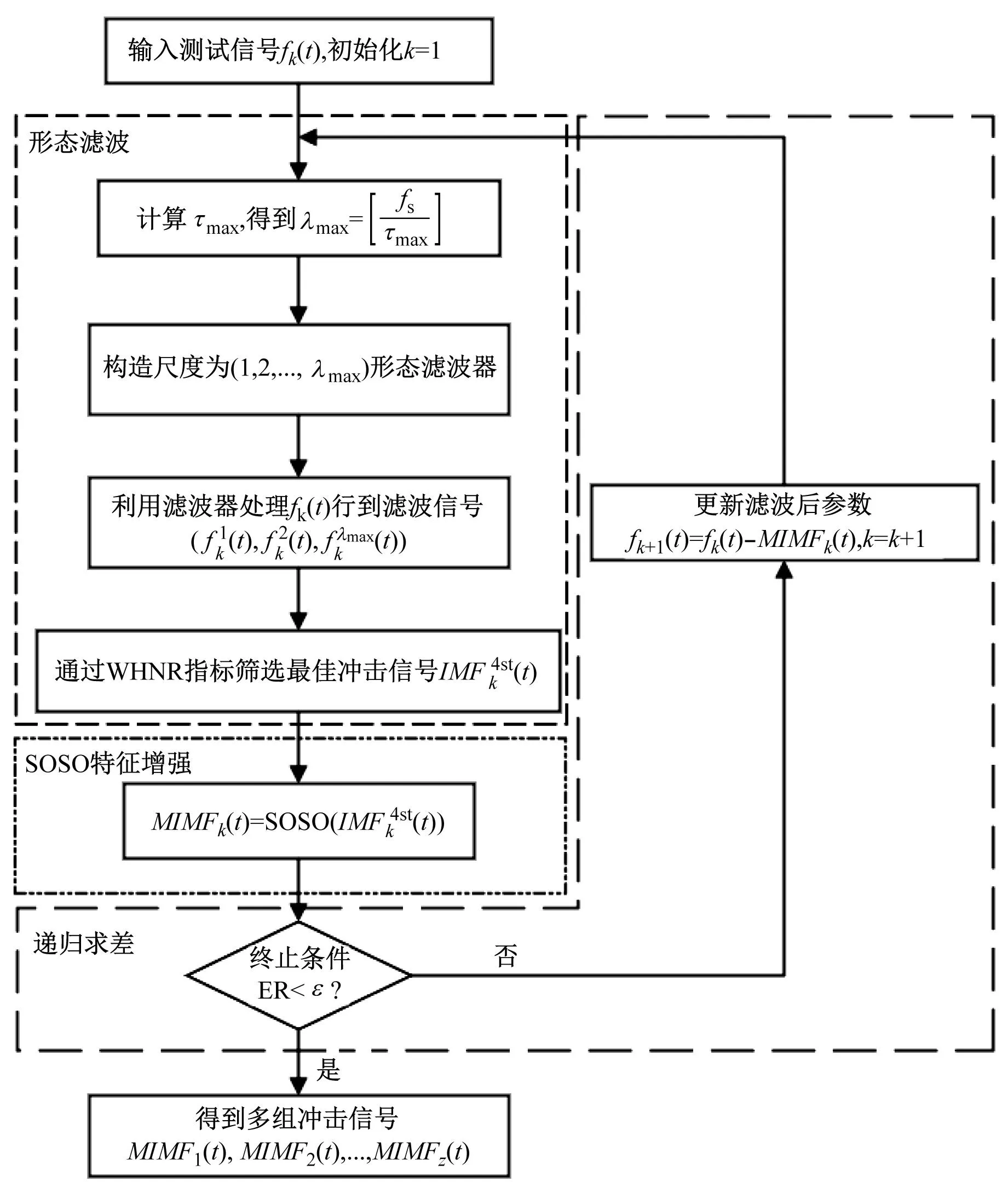
图4 本文方法分析流程图
具体实现过程如下:
步骤1输入测试信号fk(t),同时初始化参数k=1;
步骤2利用结构元素(structuring elements,SE)、CMFH算子和λmax构造多尺度形态滤波器。直线型结构元素可以避免信号幅值修改和减少运算量,故选用直线型结构元素[23]。依据式(17)确定滤波器尺度λ范围为1~λmax
(17)
式中:τmax为测试信号fk(t)自相关函数中除零位置外的最大极值位置;fs为测试信号fk(t)的采样频率。
步骤3利用多尺度形态滤波器对测试信号fk(t)进行处理得到多组滤波信号f(k,1)(t)、f(k,2)(t)、…、f(k,λmax)(t),并结合峭度指标(kurtosis,KR)和包络谐噪比[24](envelope harmonic to noise ratio,EHNR)构造加权谐噪比(weighted harmonic to noise ratio,WHNR)指标,该指标能够有效指示冲击特征和冲击特征周期性。利用WHNR指标作为滤波信号择优筛选标准,得到最佳冲击信号分量IMF(k,est)(t),WHNR指标计算公式如下
(18)
式中:μ为滤波信号f(k,λ)(t)的平均值;σ为滤波信号f(k,λ)(t)的标准差;E(f(k,λ)(t))是对滤波信号f(k,λ)(t)包络处理的时间序列;rf为E(f(k,λ)(t))的自相关函数;τmax是rf的最大位置;rf(τmax)为最大位置对应的幅值;rf(0)为包络总能量。
步骤4利用SOSO增强技术结合多尺度形态滤波算法对得到的冲击信号IMF(k,est)(t)进行特征增强,进而得到冲击信号MIMFk(t);
步骤5判断冲击信号MIMFk(t)中ER(energy ratio)是否小于能量比阈值ε,如果是,则得到z组冲击信号分量,其中z≤k,完成分离。如果否,则利用递归求差实现测试信号分离,递归求差公式为fk+1(t)=fk(t)-MIMFk(t),fk(t)为测试信号第k次循环后信号。循环终止条件为ER<ε,ER见式(19)。经过大量试验信号验证,阈值ε取0.001。
(19)
式中:EMIMFk(t)为MIMFk(t)信号幅值平方和;Efk(t)为测试信号幅值平方和。
3 仿真信号分析
3.1 滚动轴承内外圈复合故障仿真分析
为了验证本文所提方法在提取和分离冲击信号方面的优越性,模拟滚动轴承内外圈复合故障仿真信号,并添加谐波干扰、随机冲击以及强背景噪声进行分析。具体仿真信号描述为
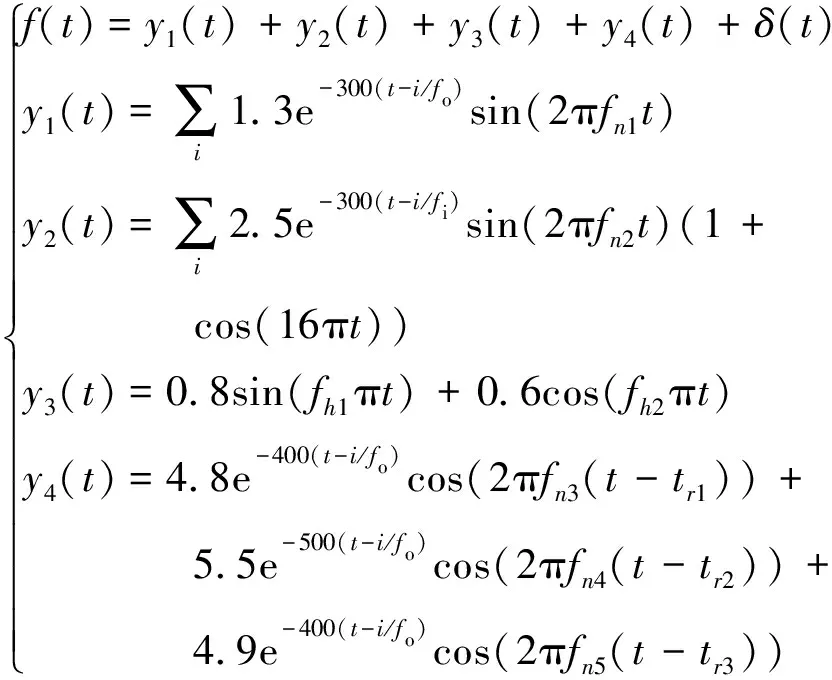
(20)
式中:f(t)为故障仿真信号1;y1(t)为轴承外圈发生故障的模拟信号,其中fo为轴承外圈故障频率;y2(t)为轴承内圈发生故障的模拟信号,其中fi为轴承内圈故障频率,fn为系统固有频率;y3(t)为谐波干扰信号,两个谐波频率fh1、fh2分别为30 Hz、50 Hz;y4(t)为随机冲击干扰信号,其中随机冲击的发生时刻分别为tr1=0.1 s,tr2=0.2 s,tr3=0.4 s,δ(t)为信噪比为-4 dB高斯白噪声。仿真信号采样频率fs=10 240 Hz,仿真时长为1 s,其参数具体数值如表1所示。

表1 仿真信号参数
滚动轴承内外圈复合故障仿真分析选用仿真信号1。仿真信号成分如图5所示。图5(a)、图5(b)分别为轴承外圈冲击和轴承内圈冲击信号,图5(c)为谐波干扰信号,图5(d)为随机冲击干扰信号。图6(a)、图6(b)分别为复合故障仿真信号1时域图和包络谱。在时域波形中可以看出故障冲击信号已经被噪声完全掩盖,在包络谱中发现谐波耦合频率(fh2-fh1=20 Hz)和内圈故障特征频率基频fi,但轴承外圈故障特征频率fo在干扰信号下无法识别,表明包络谱分析方法失效。
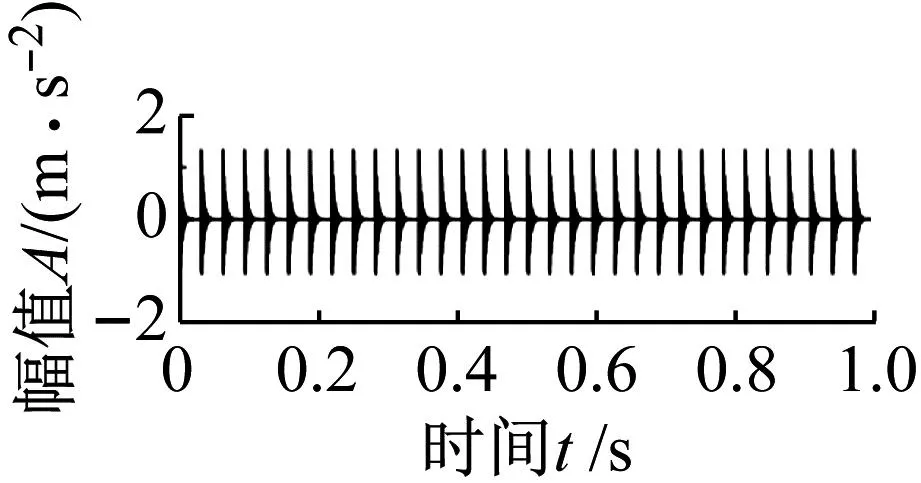
(a) 外圈冲击特征
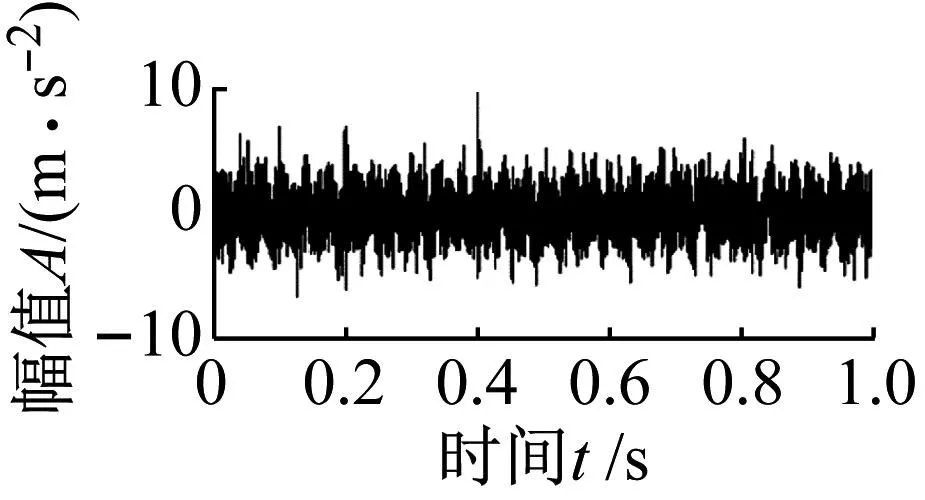
(a) 时域图
利用不添加SOSO增强的文中方法对仿真信号1进行分析,结果如图7所示。得到两组信号模式分量。其中MIMF1中包络谱发现了外圈故障基频fo、内圈故障fi和2fi,MIMF2分量中可以找到内圈故障基频fi、内圈故障fo和2fo,可以看出该方法未能有效分离出内外圈故障信号。利用本文方法对仿真信号1进行分析,结果如图8所示。得到3组故障信号模式分量,从MIMF1时域图中可以看到清晰的冲击特征,包络谱上可以清晰地找到轴承内圈故障特征频率基频及其倍频,且谱线突出;同样,从MIMF2信号包络谱中可以找到外圈故障特征频率基频及其倍频;MIMF3信号的时域图出现了三组明显的高幅值随机冲击信号,包络谱中没有发现明显的故障信息。对比图7和图8可知,包含SOSO增强算法的本文方法可以有效增强内外圈故障的局部特征,并去除随机冲击、谐波以及高斯白噪声干扰,成功分离出轴承复合故障。这验证了本文方法在复合故障分离中优势。
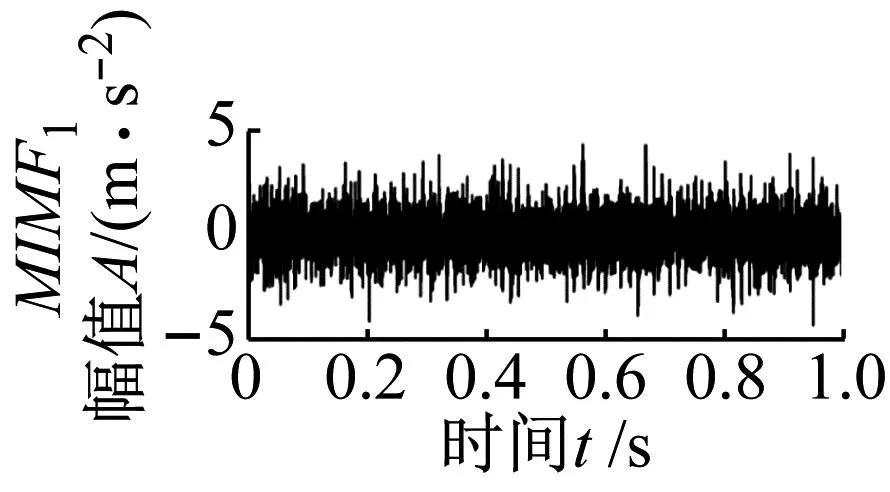
(a)
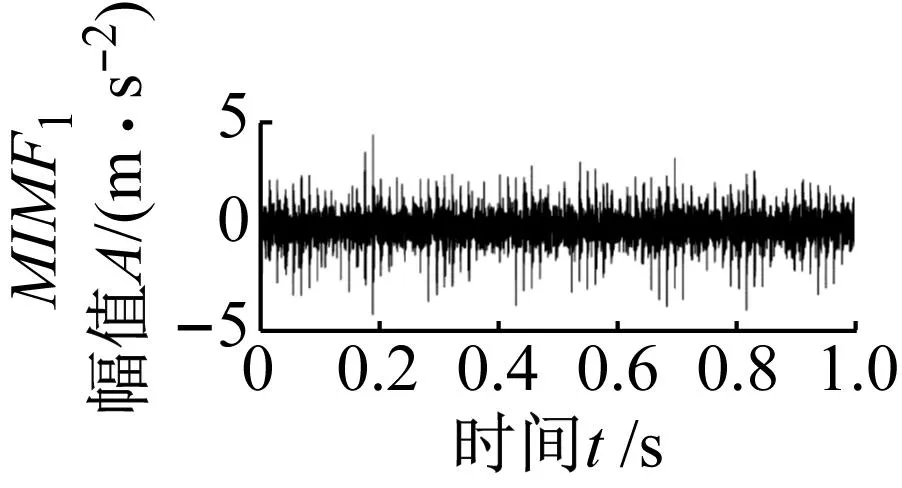
(a)
3.2 滚动轴承单一故障仿真分析
为了进一步验证本文方法在提取单一冲击故障特征方面的有效性,选用仿真信号1中的y1(t)、y2(t)、y3(t)和δ(t)分量构造仿真信号2,如图9所示。在图9时域波形中可以看出,故障冲击信号已被噪声完全掩盖,包络谱中无法有效识别出轴承外圈故障特征频率fo及其倍频。
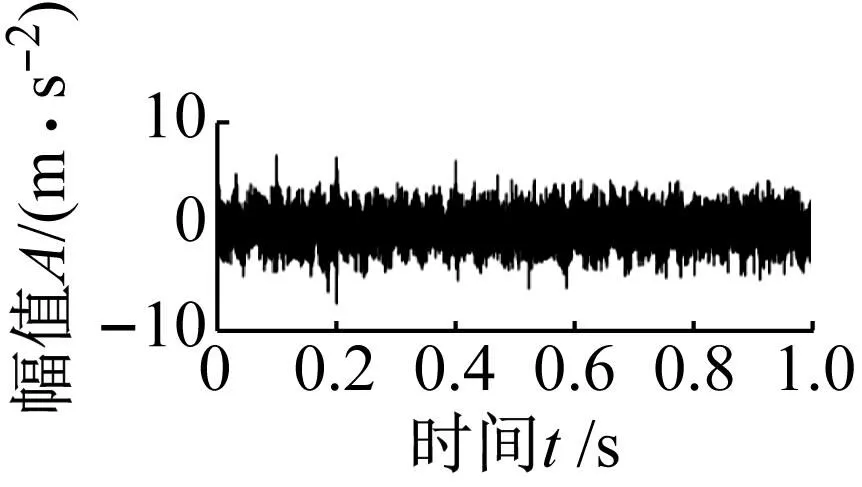
(a) 时域图
利用不添加SOSO增强的文中方法对仿真信号2进行分析,结果如图10所示。从图10中MIMF1分量包络谱可以发现轴承外圈故障频率fo以及2~4倍频;MIMF2分量中也可以找到外圈故障基频fo,可以看出该方法可以实现轴承外圈故障信号提取。利用本文方法对仿真信号2进行分析,结果如图11所示。MIMF1分量时域图中呈现明显的冲击成分,包络谱中可以看出轴承外圈故障特征频率基频及其2~8倍频,可以判断轴承发生了外圈故障。MIMF2和MIMF3信号时域图和包络谱没有发现明显的故障特征信息。这表明本文方法可以有效提取单一冲击故障特征。对比图10和图11可知,SOSO增强方法有效去除了噪声对外圈故障特征提取的干扰,增强了轴承外圈冲击故障特征的局部特征,使得故障特征频率在谱线上更加明显。
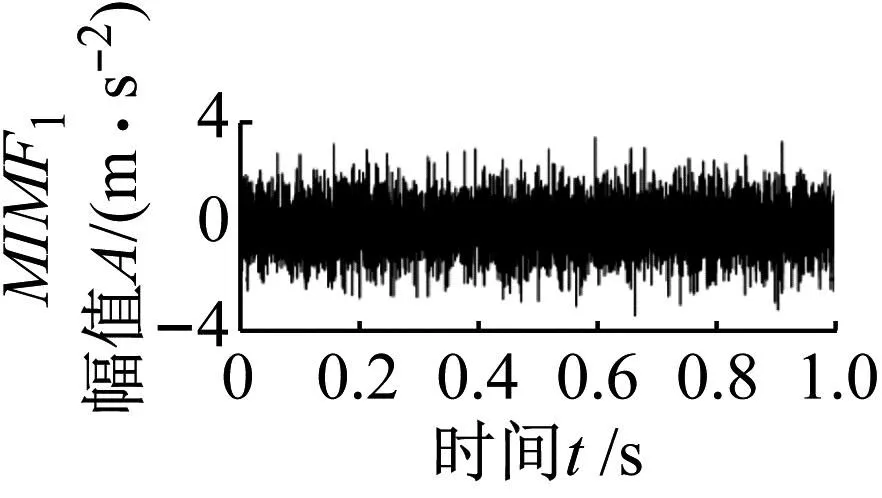
(a)
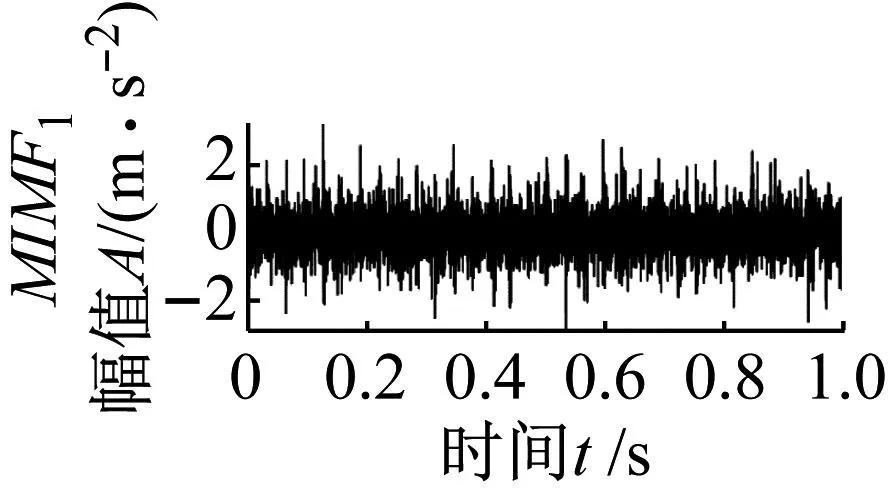
(a)
4 试验数据验证
以YQ-365型异步牵引电机中圆柱滚子轴承为研究对象,振动数据由图12中的传感器b获得。圆柱滚子轴承安装在电机内部的主轴上。电机结构简图如图13所示。

图12 YQ-365异步牵引电机
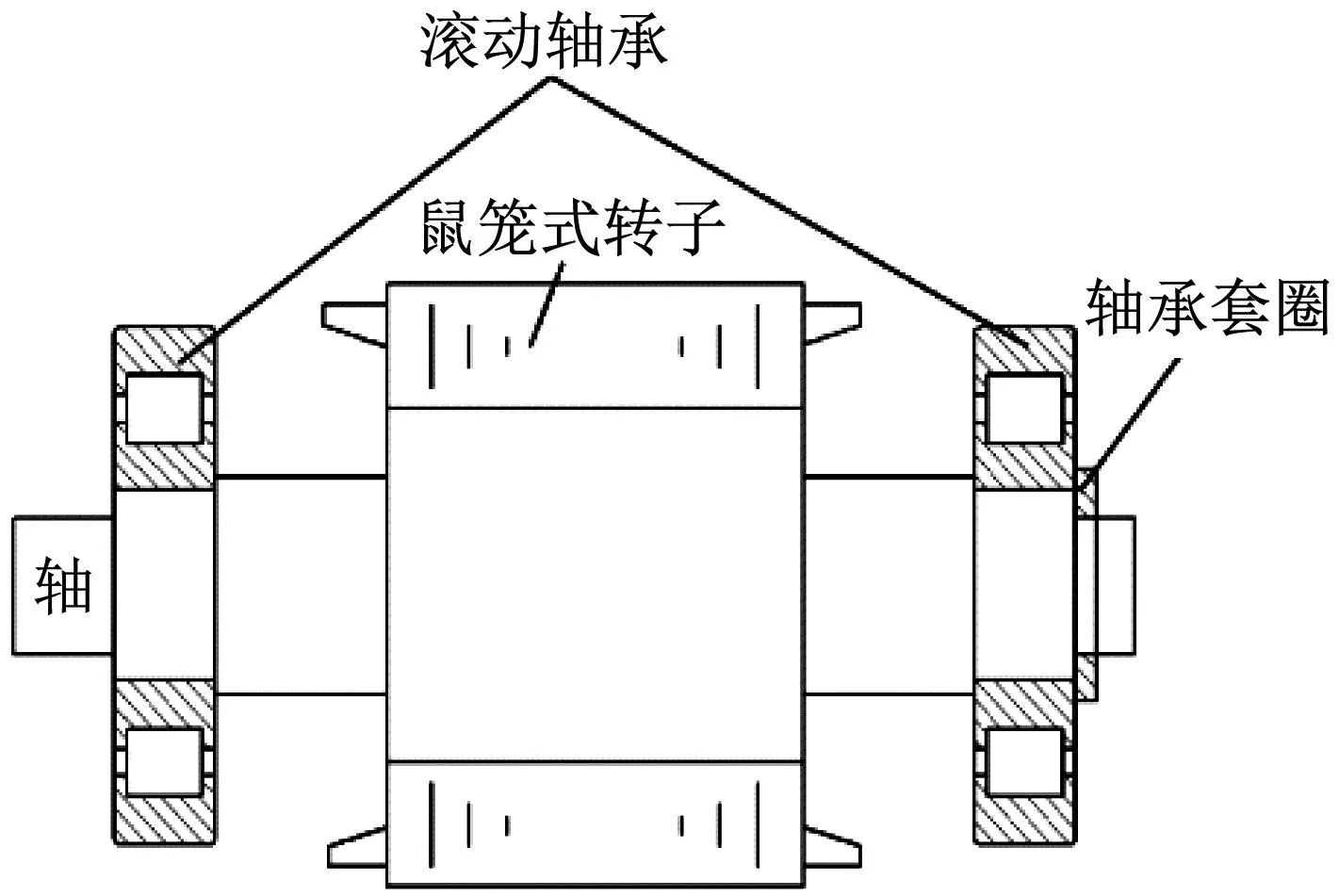
图13 电机内部结构
4.1 圆柱滚子轴承内圈故障
在进行异步牵引电机的滚子承内圈故障试验中,采用线切割方式在输出轴轴承(型号:NU214 C4)上加工内圈故障尺寸为4×20 mm的细槽,用于模拟内圈微小故障。以12.8 kHz采样频率采集振动信号。图14为轴承内圈故障的实物图。电机转速为600 r/min,根据轴承型号轴承故障频率计算公式得到轴承内圈故障特征频率fi为80.56 Hz。图15(a)为传感器所采集到的振动波形,直接对该信号进行包络谱分析如图15(b)所示,从包络谱可以找到转动频率fr及其二倍频,但无法判别是否存在轴承故障。

图14 轴承内圈损坏
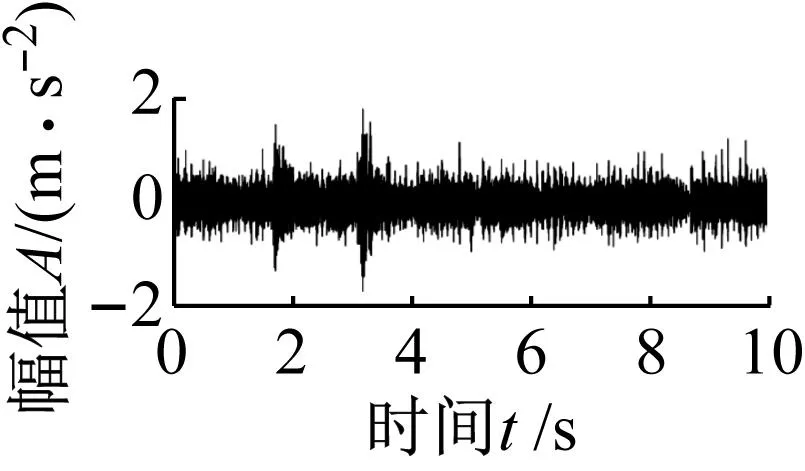
(a) 时域图
采用本文所提方法对实测信号1进行分析,结果如图16所示,从图中可以看出,MIMF1信号时域图中随机冲击成分被成功剔除,强化了冲击性特征,包络谱中找出轴承内圈故障特征频率fi和转频fr,以及转频fr的2~6倍频。MIMF2信号包络谱中只找到转动频率的基频fr。可以判定该轴承内圈发生故障。
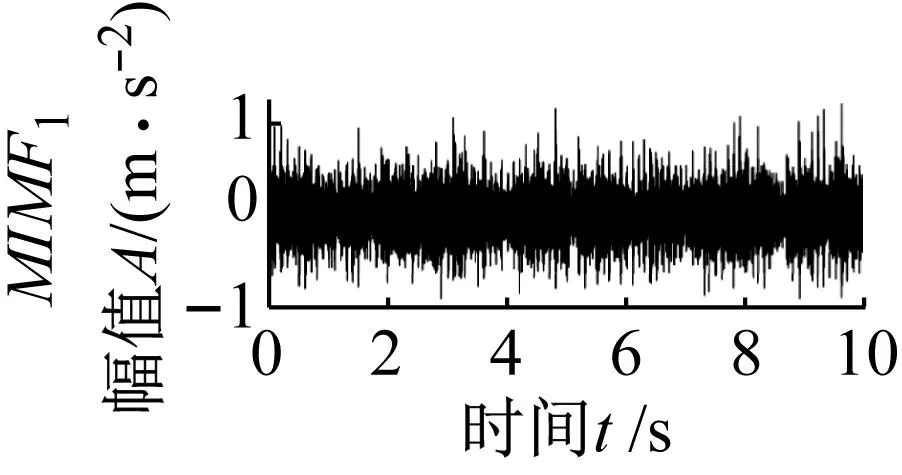
(a)
利用CYCBD[25]、匹配追踪[26]、自适应噪声完全集合经验模态分解[27](complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN)三类不同冲击特征提取方法对实测信号1进行处理,并与本文方法处理结果对比分析。三个对比方法关键参数设置如下:
(1) 利用粒子群优化算法预先确定CYCBD算法参数,最终将CYCBD滤波器的长度和特征频率值分别设置为312和80 Hz。
(2) 分析实测信号1,利用Gabor解析字典,设置字典参数范围分别为:波形尺度参数Sf为[0.1∶0.005∶5],时移参数Uf为[0.1∶0.01∶10],频率参数βf为[1∶1∶6 400]。
(3) 利用CEEMDAN算法对实测信号1分解产生14个IMF分量,通过各模式能量含量和白噪声特性确定最佳的滤波信号。
三个对比方法分析结果如图17~图19所示。图17展示CYCBD方法分析结果,在时域图中可以看到两个十分明显的随机冲击特征,但包络谱中未能找到有关内圈故障的特征成分;图18展示匹配追踪分析结果,时域图中既包含随机冲击信号也包含周期性的冲击特征,包络谱出现转频fr及其2倍频,如果想去除随机冲击,需要进一步优化原子库和匹配规则;图19展示CEEMDAN算法对实测信号1处理结果,从时域图中可以找到明显的冲击特征,随机冲击干扰得到有效去除,但包络谱只能发现转频fr及其2倍频,无法判别轴承是否出现故障;通过对三种方法结果分析得出,CYCBD和匹配追踪方法受随机冲击干扰较大,CEEMDAN分解方法消除随机冲击干扰影响,但受背景噪声干扰较大,无法有效提取出轴承故障特征,相比之下,本文方法提取故障特征效果更佳。
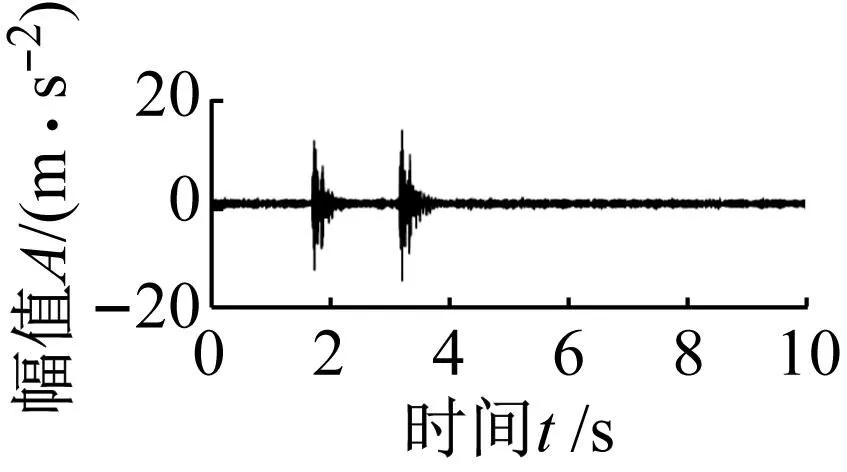
(a) 时域图

(a) 时域图
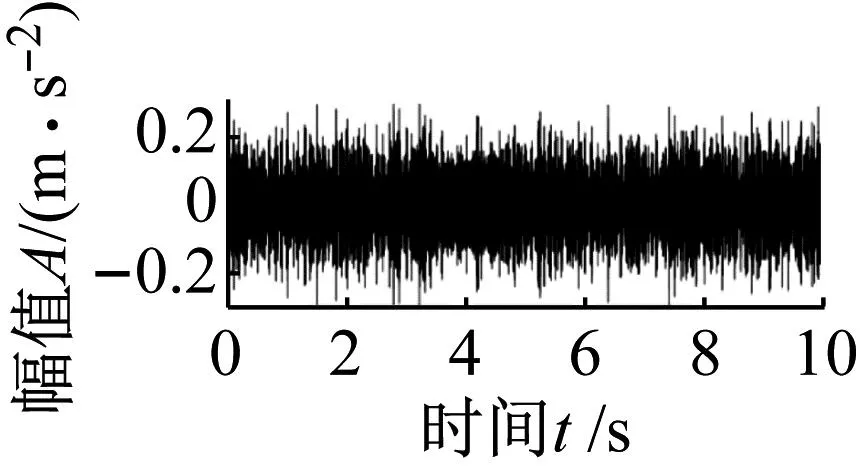
(a) 时域图
4.2 圆柱滚子轴承内圈和滚动体故障
同样在YQ-365异步牵引电机上进行圆柱滚子轴承内圈和滚动体复合故障试验,采用线切割方式在输出轴承(型号:NU214 C4)上加工滚动体故障尺寸为20×0.25 mm,内圈故障尺寸为8×0.25 mm的细槽,用于模拟内圈和滚动体故障。实物如图20所示。采样频率为12.8 kHz,数据长度为102 400个点,电机转速为600 r/min。轴承故障特征频率如表2所示。

表2 轴承特征参数

(a) 内圈损坏
本次试验采集得到实测信号2,其时域波形和包络谱如图21所示。由于受到背景噪声干扰,时域图中无法找到较明显的故障冲击,包络谱中只发现保持架的故障频率fc及其二倍频,但未发现滚子轴承内圈和滚动体故障特征。表明包络谱分析方法失效。
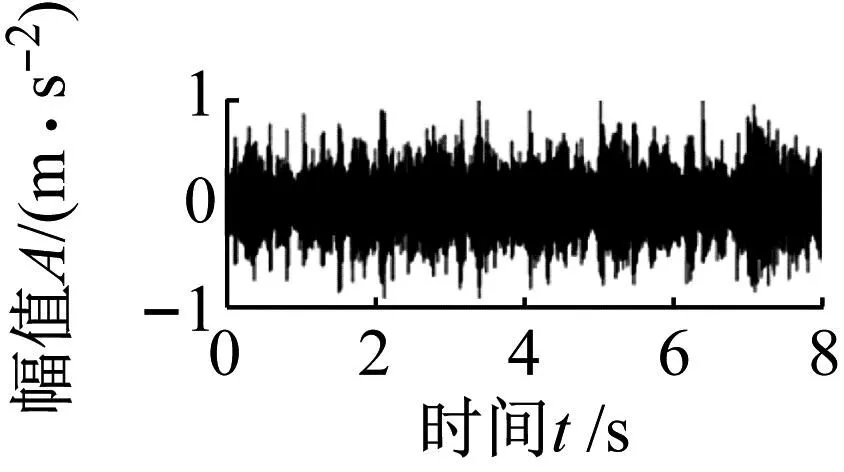
(a) 时域图
应用本文所提方法对实测信号2进行分析得到图22所示结果。在MIMF1时域信号中冲击特征明显,噪声成分有所降低,包络谱中可以找到轴承内圈故障特征频率fi和调制频率fr,以及频率fr的2~4倍频。MIMF2信号中背景噪声得到有效去除,包络谱中发现滚动体故障特征频率fb及其2倍频,以及调制频率fc及其2、3倍频。在MIMF3信号包络谱只找到保持架基频fc及其2倍频。根据分析结果可判断出轴承滚动体和内圈同时发生故障,诊断结果与实际情况完全相符。
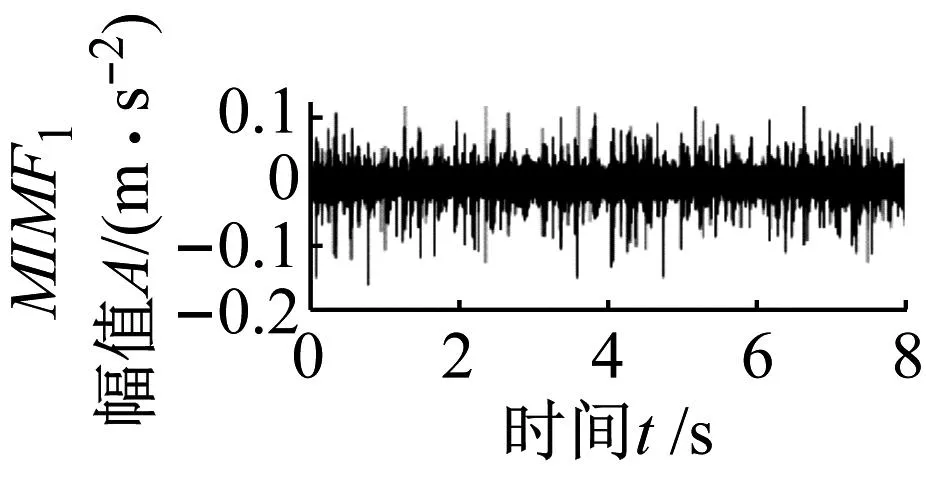
(a)
为验证本文方法优越性,利用快速谱峭度[28]、匹配追踪[29]和双约束非负矩阵分解[30]三类不同冲击特征提取方法对实测信号2进行分析,图23为快速谱峭度分析结果。取图23中2个较明显的共振频带(白色实线框),共振频带中心频率分别取1 860 Hz和5 980 Hz,对应带宽分别为332 Hz、286 Hz。利用共振解调分别得到2个共振带进行包络谱分析,结果如图24所示。从谱图中可以看出该方法可以提取出转动频率,但并未找到轴承的故障特征频率。与图22结果比较,快速谱峭度方法仅仅增强了轴承转频fr,不能识别出轴承故障特征。利用匹配追踪方法对实测信号2进行分离处理,得到两组分离信号如图25所示。其中分离信号1时域图中出现明显的冲击特征,包络谱中可以识别出滚动体故障特征频率fb、调制频率fc及其2、3倍频,分离信号2包络谱中仅找到调制频率fc及其3倍频。与图22结果比较分析得知,匹配追踪方法在分析实测信号2中的复合故障时效果不佳,可以提取出滚动体故障特征,但不能识别出轴承内圈故障特征。利用双约束非负矩阵分解方法对实测信号2进行处理,结果如图26所示。分离信号1包络谱中可以找到调制频率fc的二倍频,分离信号2包络谱中也同样只找到调制频率fc的二倍频,分析可知双约束非负矩阵分解方法在分析实测信号2中的复合故障时效果不佳。经过上述分析可知,本文方法在处理复合故障特征分离问题上有自身优势。
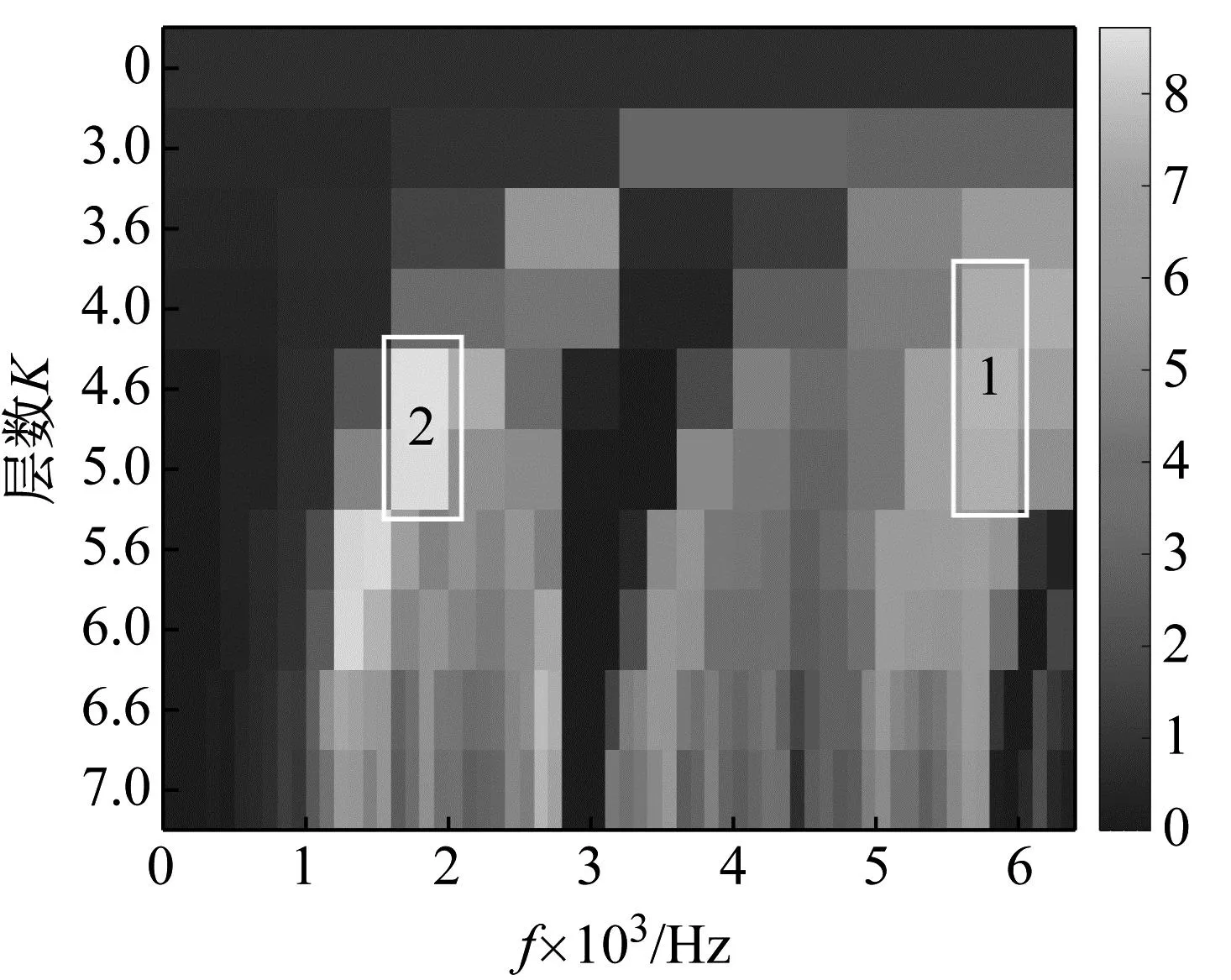
图23 实测信号2快速谱峭度图

(a) 共振带1
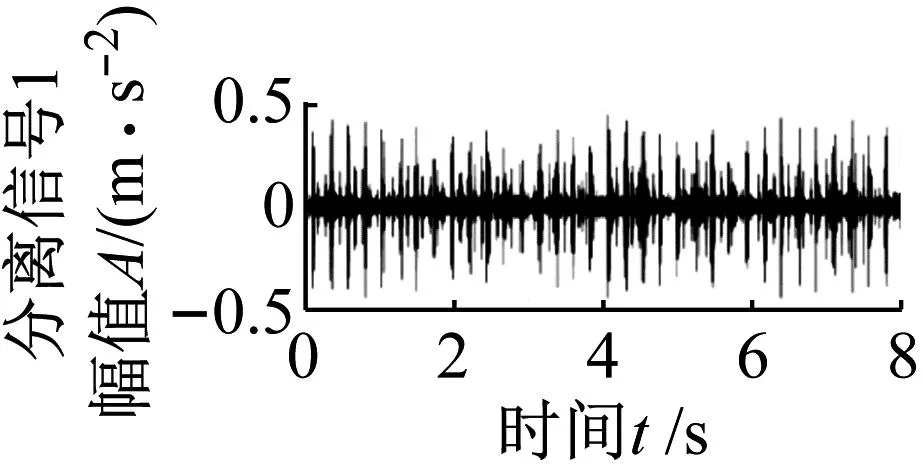
(a)
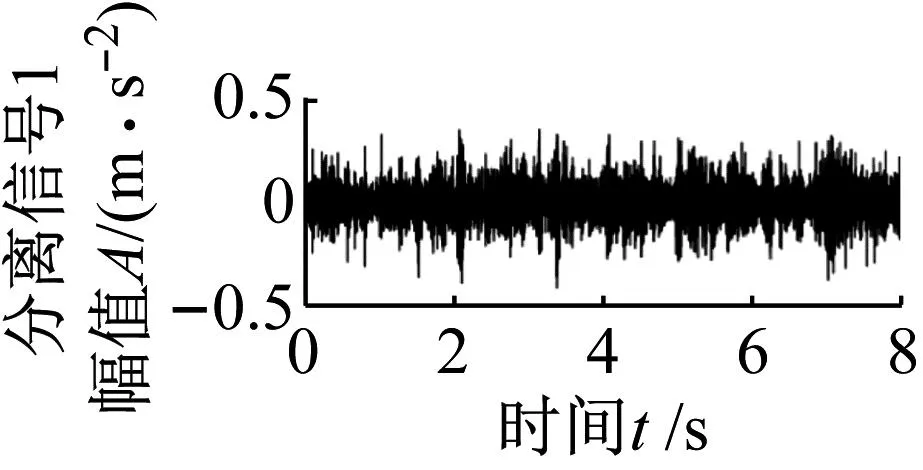
(a)
5 结 论
(1) 利用EA指标和频响特性分析,从典型组合算子中(AVG、ACDIF、DIF、MG、CMFH)筛选出适合冲击特征分离的CMFH形态学算子。
(2) 将多尺度形态滤波、加权谐噪比、SOSO增强技术以及迭代求差思想结合,提出一种冲击特征提取和逐级分离方法。该方法可以实现复合冲击有效分离,且无需预设参数,不易受随机冲击和谐波影响。
(3) 利用轴承单一故障和复合故障试验数据验证了所提方法的鲁棒性和优越性。与CYCBD、匹配追踪、CEEMDAN方法、快速谱峭度和双约束非负矩阵分解方法比较,所提方法在随机冲击、强背景噪声干扰下的单一弱冲击特征提取,以及复合冲击特征分离中具有一定的应用价值。

