基于响应复合能量因子的波浪激励下高桩码头桩基损伤识别
李成明,王启明,3,朱瑞虎,胡 艳,王泊淳
(1.河海大学 数学学院,南京 211100;2.河海大学 港口海岸与近海工程学院,南京 210098;3.河海大学 海岸灾害及防护教育部重点实验室,南京 210098)
高桩码头是我国港口中重要的码头形式之一。在其服役期间,常因船舶撞击、海水腐蚀等原因导致桩基损伤,致使承载能力下降,严重情况下会危及码头安全。因此,对桩基进行损伤识别和健康监测具有重要的意义和价值[1-2]。目前,工程中常用的桩基损伤识别方法为静载法、低应变法和高应变法[3-5]。三者均需要在桩身切出传感器安放平台和激振平台,过程费时费力且会对桩基安全性和耐久性造成不利影响,无法实现真正的无损检测[6]。
随着监测技术及光纤传感设备的不断发展,基于动力指纹(主要是频率、模态及衍生指标)的桩基无损诊断的研究成为研究热点。孙熙平等[7]提出了一种环境激励下高桩码头NExT-ERA模态参数识别方法,通过该方法能够较准确地识别基桩损伤部位。李肖等[8]提出一种基于曲率模态的桩基损伤识别方法,该方法通过损伤后的真实曲率模态相对于拟合曲率模态的突变来判别损伤位置。王启明等[9]研究了1阶频率对应的模态柔度在高桩码头桩基损伤识别中的适用性,通过试验与数值模拟表明该方法能准确定位桩基损伤位置,且具有较好的鲁棒性。朱瑞虎等[10]通过建立高桩码头模型,采用有限元数值模拟和模型试验验证了模态应变能在高桩码头桩基损伤识别中的适用性。Wang等[11]提出了一种基于曲率模态差的桩基损伤识别方法,并通过数值和物理模型试验验证了该方法的有效性。Zhu等[12]提出一种基于多维动力指纹的损伤识别方法,该方法利用马氏距离定义受损单元与未损伤单元之差,通过有限元模型和试验结果表明该方法具有较强的应用潜力。但是,模态参数识别依赖于外部激励形式以及数值算法,由于高阶模态易受外部噪声影响,现有结构健康监测都是基于结构的低阶模态诊断损伤[13];同时,由于模态参数识别的误差,模态特征对局部损伤检测的敏感性不足,且对于较小的损伤,模态分析的损伤定位能力不显著[14-15]。
在实际应用中,获取码头动力指纹通常需要船舶撞击等手段进行激励,成本高且影响码头安全。波浪是影响桩基健康的一种重要且长期的外部激励[16],研究波浪激励下动力响应对桩基的健康诊断具有重要意义。然而,由于波浪激励是一个窄带随机过程,这与模态参数识别的白噪声激励和脉冲激励条件相悖[17],根据波浪激励下动力响应获得的动力指纹误差较大,易对损伤产生误判和错判。因此,基于信号分解与统计推断的损伤识别方法逐渐受到学者们的关注[18-20],该技术通过获取结构在各种情况下的振动特征,进而构造统计指标反映结构损伤情况[21]。Hilbert-Huang变换(Hilbert-Huang transform,HHT)由Huang等[22]提出,其包含经验模态分解(empirical mode decomposition,EMD)和Hilbert变换两个过程。一般先利用EMD将信号分解为本征模态函数(intrinsic mode functions,IMFs),再利用Hilbert变换求得一系列特征。这种信号处理方法是完全自适应的、不受Heisenberg测不准原理制约,且适用于非线性、非平稳信号的分析[23]。但EMD存在一个固有缺陷,即模态混叠[24]。鉴于此,Torres等[25]提出了自适应噪声的完备集成经验模态分解(complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN),该分解方法得到的结果中噪声被大大减少,并且显著改善了模态混叠现象。
众多学者基于上述算法处理复杂结构动力响应信号,并将其应用于结构损伤识别领域。Zhu等[26]结合EMD、主成分分析和独立主成分分析构建了一种温度诱导响应提取方法,并通过桁架桥试验验证了通过移动主成分分析能提高发现损伤的概率。Xiao等[27]提出一种移动车辆条件下桥梁特征提取方法,该方法对加速度信号使用CEEMDAN和Hilbert变换提取Hilbert谱,结合有限元分析证明了该方法对谱特征的提取更具优势。Mousavi等[28]基于CEEMDAN对原始信号进行分解,利用多信号分类算法求得IMFs的空间频谱,以此反映损伤前后频率变化,通过桁架桥模型试验证明了该方法优于传统频域分析技术。基于EMD及其衍生算法在海洋领域的应用也陆续展开,Hu等[29]基于EMD和谱特征分析,构造了一种提取波浪激励下动力响应特征的新方法,结果显示提取的信号具有稳定性,有效提高了损伤识别的可靠性。Yang等[30]为提高复杂海洋环境下船舶辐射噪声特征的提取水平,结合CEEMDAN和能量构造分配比率作为特征向量的估计,利用自组织映射实现特征提取。Li等[31]基于CEEMDAN提出一种海洋环境下水声去噪技术,该方法先将信号分解为IMFs,进而构造互信息、排列熵等特征进行噪声剔除,通过模拟数据与试验仿真验证了该方法的有效性。现有成果表明CEEMDAN在精确度、复杂度、可用度等方面较其他方法存在优越性[32]。而同时,高桩码头作为一种超静定结构,其在波浪激励下基于CEEMDAN的动力响应分解、特征信号提取及损伤识别指标构建缺乏系统研究。
本文针对波浪激励下桩基动力响应非线性、非平稳、多类型信号混叠的特性,结合CEEMDAN与K-means++构建自动信号分解与重构方法,从中提取损伤特征子信号。针对单一特征在损伤识别效果方面的不足,本文基于能量与相位提出一种新型复合能量损伤识别因子。进一步,设计波浪激励下高桩码头桩基损伤试验,以研究新策略在高桩码头桩基损伤识别中的有效性与敏感性。结果表明,复合能量因子能有效改善损伤识别效果,成功识别出损伤存在、损伤位置与损伤程度。
1 桩基动力响应重构与损伤指标构造
波浪激励下桩基动力响应由多类型信号混叠而成,通过CEEMDAN能够将其分解为多个分量,进而构造IMFs分类函数重构获得不同类型的响应,最后针对损伤敏感信号提取特征并构造损伤指标用于损伤识别。
1.1 动力响应信号分解方法
EMD方法首先是对原始信号求取局部最大值和局部最小值,然后拟合上下包络线,并计算两者的均值。如果该均值同时满足以下两个条件,则称其为一个IMF分量:① 在整个时间范围内,局部极值点与零点个数相等或至多相差一个;② 在任意时刻,上下包络线的均值必须为0。若不满足条件,则用原始信号减去该均值得到一个新的残差序列,对该序列重复上述过程,直到满足以上两个条件。
CEEMDAN方法中IMF1的计算首先对原始信号多次添加白噪声形成若干新信号,再利用EMD对这些信号分别进行分解,对多组分解结果中IMF1进行平均得到最终结果,计算IMF2时需要对残差项多次添加白噪声经EMD分解后的IMF1形成若干新信号,再对这些新信号进行EMD得到IMFs,最后对多组IMFs中IMF1进行平均得到IMF2,后续IMF分量的计算重复该过程。
利用CEEMDAN最终得到n个IMF及1个残差项r(t),即:
(1)
式中,x(t)为时间样本数为T的原始信号。
功率谱密度(power spectral density,PSD)的计算将原始信号x(t)看作能量有限的序列,假设N=2M,M取当N≥T时的最小正整数,对原始信号进行快速傅里叶变换得到FFT[x(t)]。从而得到功率谱密度的估计值
(2)
式中,fs表示采样频率。PSD第k个值对应的频率为
(3)
CEEMDAN得到的结果中包含多个类型的信号及存在模态混叠现象,并且为了获得损伤特征子信号,需要对IMFs进行重构。为了辅助分类,首先对每个IMF的PSD进行积分,得到频率fk处的累积谱分布(cumulative spectral distribution,CSD),以获取其频谱特征[33]
(4)
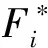
上述方法缺点在于分类时需要人为设定阈值点,不利于构建结构健康监测体系。聚类分析作为数据挖掘的技术之一,通过将数据自动分为不同的簇,从中发现相似的对象或信息[34]。K-means++是对K-means聚类算法的改进,其主要优势在于改进了初始中心点的选择方式,通过引入随机概率的方式选择中心点,避免了传统K-means算法中随机初始化中心点可能带来的局部最优解问题,从而可以提高聚类的准确性和鲁棒性[35]。本文将CSDs视为数据对象,采用K-means++对具有共同数据特征的对象进行聚类[36],从而实现IMFs的自动重构。为了得到更好的聚类效果,选择欧式距离作为同步度量,并在聚类前对CSDs进行标准化,公式为
(5)
此外,本文选择轮廓系数为最佳聚类数提供参考[37],假设样本i被归为簇A,样本对应的轮廓系数及该次聚类的轮廓系数定义为
(6)
(7)
式中:a(i)为样本i与同簇其他样本的平均距离;b(i)为样本i到其他簇中样本平均距离的最小值。轮廓系数取值范围为[-1,1],其值越大说明选择该值对应的聚类数得到的聚类结果越合理、有效,通过轮廓系数曲线可以对分类数选择进行判定。
1.2 损伤指标的构造
结构性的损伤会导致振动信号某些特征发生改变,根据这一特点,本节对提取的损伤特征子信号进行Hilbert变换,从中提取瞬时振幅、相位等特征,以此构造相应的损伤指标用于对高桩码头桩基的损伤识别。
Hilbert变换是得到多个特征的基础,该变换的公式为
(8)
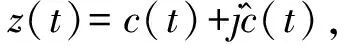
(9)
(10)
当系统本身的结构发生变化或系统的状态变成异常状态时,系统自身的能量也会随之变化,所以能量通常能较好地反映结构损伤[38-39]。瞬时能量及某个信号能量的计算公式为
(11)
(12)
在得到能量和相位特征后,分别基于两者构造相应的损伤指标[40]
(13)
(14)
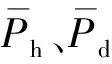
根据Cheraghi等[41-42]的研究,振动信号和结构刚度的任何变化都会引起能量和相位的变化。因此,当结构损伤出现时,DI(E)和DI(P)的值也会改变,从而反映结构响应的突变。Mousavi 等通过钢桁架桥模型敲击试验验证了DI(E)和DI(P)都包含结构损伤位置、损伤程度信息,且DI(E)的识别效果优于DI(P)。由于波浪激励下桩基动力响应非平稳、信噪比低、多类型混叠等原因,本文综合考虑将两者融合,基于能量和相位构建一个更敏感的组合损伤指标,以此提高对桩基损伤识别的敏感性和鲁棒性,达到准确识别桩基损伤存在、损伤位置与损伤程度的效果。基于DI(E)和DI(P)构建复合能量因子
(15)
图1为本文流程图,展示了由试验到损伤识别的过程。
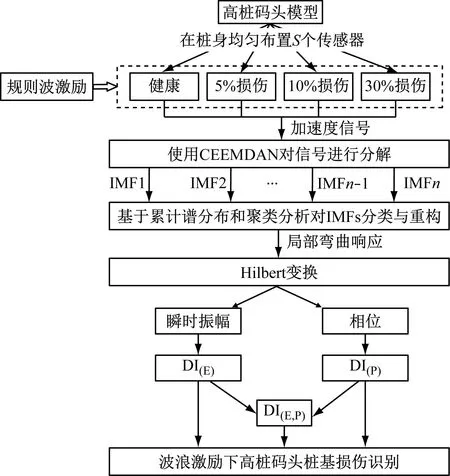
图1 波浪激励下桩基损伤识别流程图
2 基于模型试验的验证
为了更好揭示波浪激励下桩基动力响应的规律性,本文在实验室条件下建立了高桩码头桩基模型,用于研究桩基损伤识别理论与方法。在此基础上,对试验信号进行分解并提取目标信号,进而构造损伤指标实现对波浪激励下高桩码头桩基的损伤识别。
2.1 试验介绍
本试验在河海大学港口航道工程与海岸海洋科学实验中心完成。模型长0.9 m、宽0.75 m、高1.65 m,共1跨,排架间距为0.65 m,码头前沿和中间为单直桩,后方为一对叉桩,桩身采用直径0.06 m、壁厚2 mm的Q235钢管桩,码头上部横梁、纵梁、面板采用钢筋混凝土浇筑,桩顶设置桩帽,钢管桩顶部伸入桩帽,使得桩身与上部结构之间的连接为固定连接。在模型设计时根据研究内容对边界条件进行了部分简化,本文重点研究桩基泥面以上的动力损伤识别,考虑实际工程中桩基固结深度以下实际位移为零,所以将模型底部设计为固结,模型如图2所示。
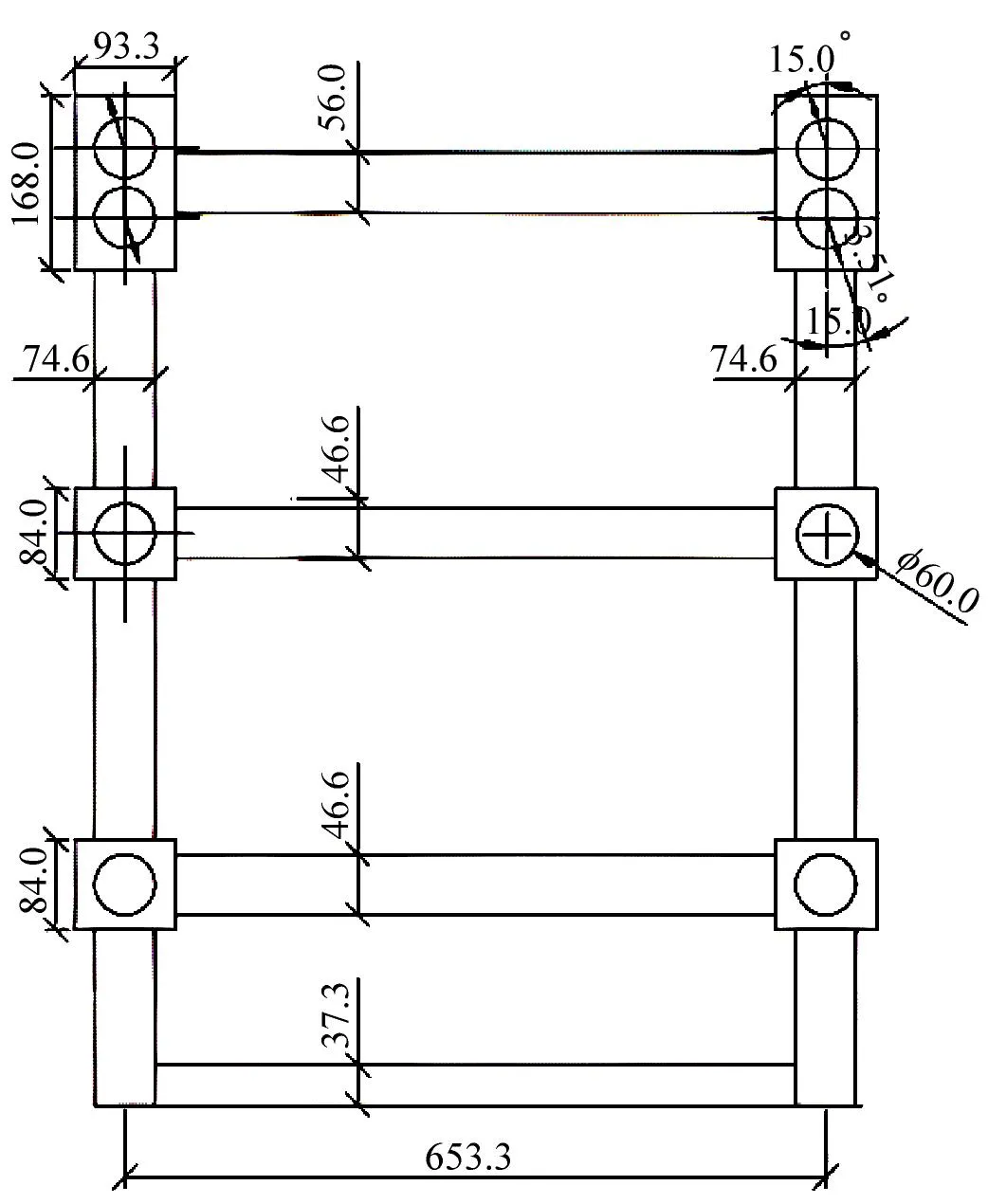
(a) 模型俯视图
试验所用风、浪、流水槽长85.0 m、宽1.0 m、高1.5 m,如图3所示。配备带有二次反射波全吸收装置的伺服电机型水槽,具有不规则波浪造波机、循环水流系统、加风系统等设备,能模拟波高0~0.3 m、波周期0.5~5 s的规则波与不规则波,具备研究海洋建筑物在二维规则与不规则波作用下的各种动力响应机制的能力。

图3 试验水槽
码头直桩基长为1.3 m,其被平均分成13段,每段长0.1 m。拾振器采用YD-186型压电式加速度传感器,传感器布置在桩身的节点位置,模型节点编号和传感器布置如图4所示。为了模拟实际工程中浪溅区损伤桩基的情况,损伤设置在图4(a)中节点5~6之间。损伤工况为刚度EI(E为弹性模量,I为截面惯性矩)分别下降5%、10%、30%得到。试验中采用改变结构几何尺寸减小截面惯性矩实现刚度下降。高桩码头模型桩身为圆环截面,圆环截面轴惯性矩计算公式如下
(16)

(a) 区段分布图
式中:D为圆环外圆直径;d为圆环内圆直径。计算得到截面缝宽如表1所示。损伤位置及传感器位置与波浪方向的关系如图5(a)所示。
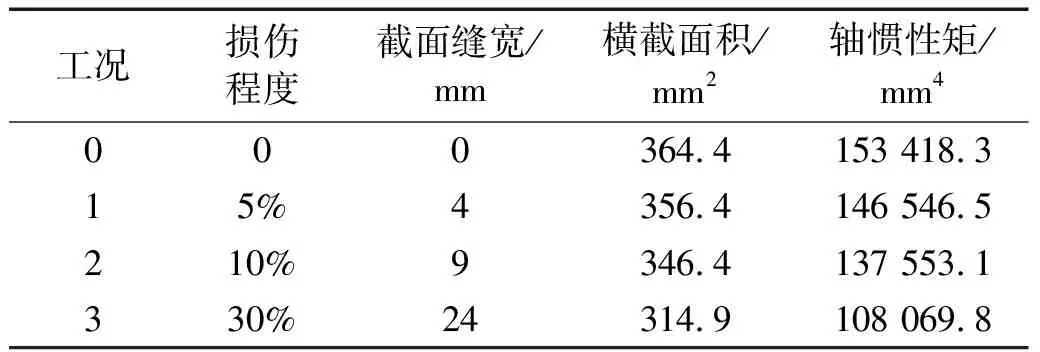
表1 试验损伤工况设置
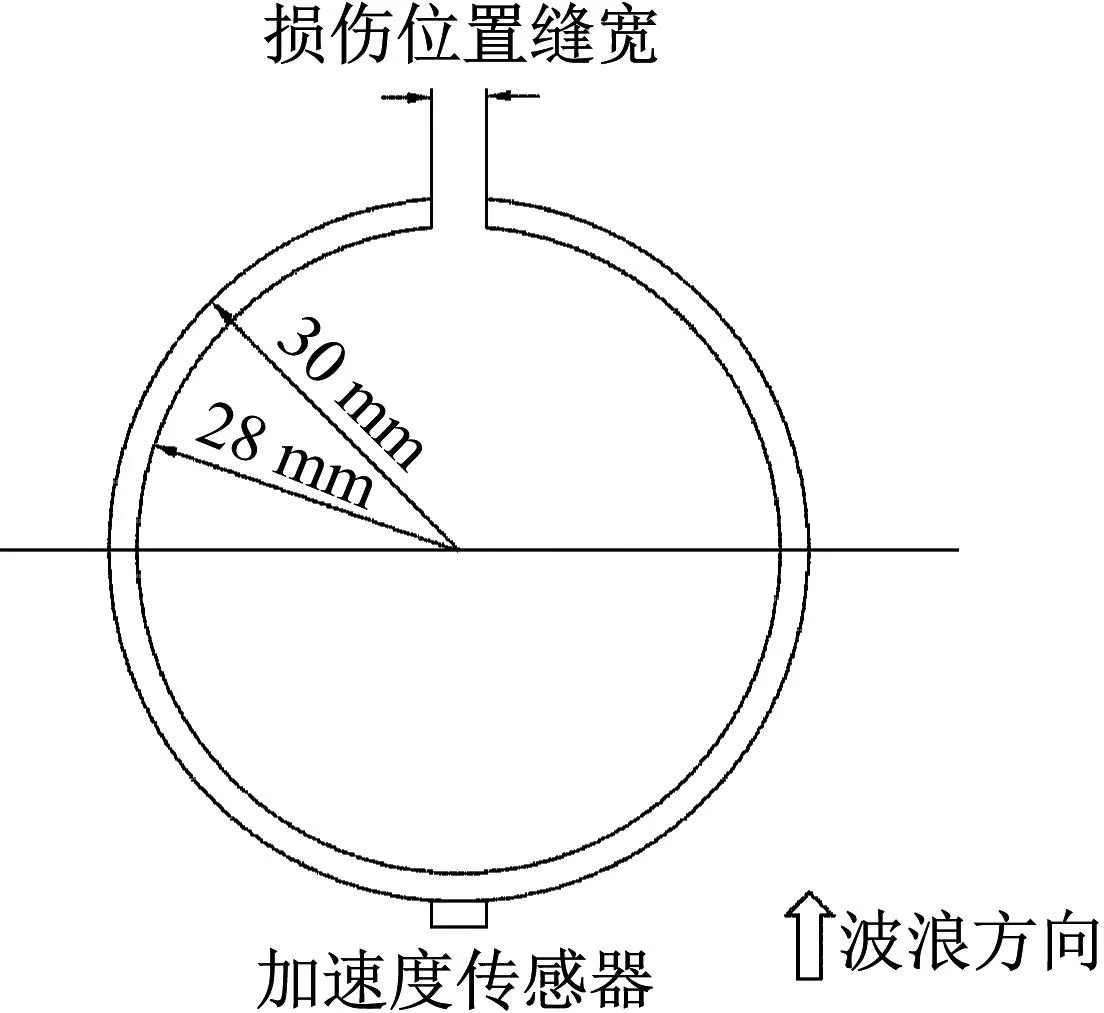
(a) 损伤桩的横截面
本试验采用水深1.0 m,周期1 s,波高为0.1 m的规则波作为外部激励。采集设备采用DH5920动态信号采集分析系统,该系统可实现多通道并行同步采集,单通道采样频率为1 000 Hz,测试方向为来波方向,以此获取波浪激励下桩基模型在不同损伤程度下13个节点的加速度信号。
2.2 动力响应信号分解与损伤特征子信号的提取
损伤5%工况下获取的节点5处加速度信号如图6所示。可以看出,该加速度信号由表示不同物理过程的信号(包含漂移项、周期信号、冲击信号等)共同组成。分解结果及对应的PSD如图7~9所示,图中IMFs由高频向低频排列。可以看出,虽然CEEMDAN是EMD算法的改进,但在复杂波浪激励环境下得到分解结果仍存在部分模态混叠现象,如IMF1~IMF2的频率在300 Hz附近,IMF3~IMF4的频率均在100 Hz,即相同频率或尺度的信号分布在不同的IMF分量中,所以需要对其进行分类与重构。
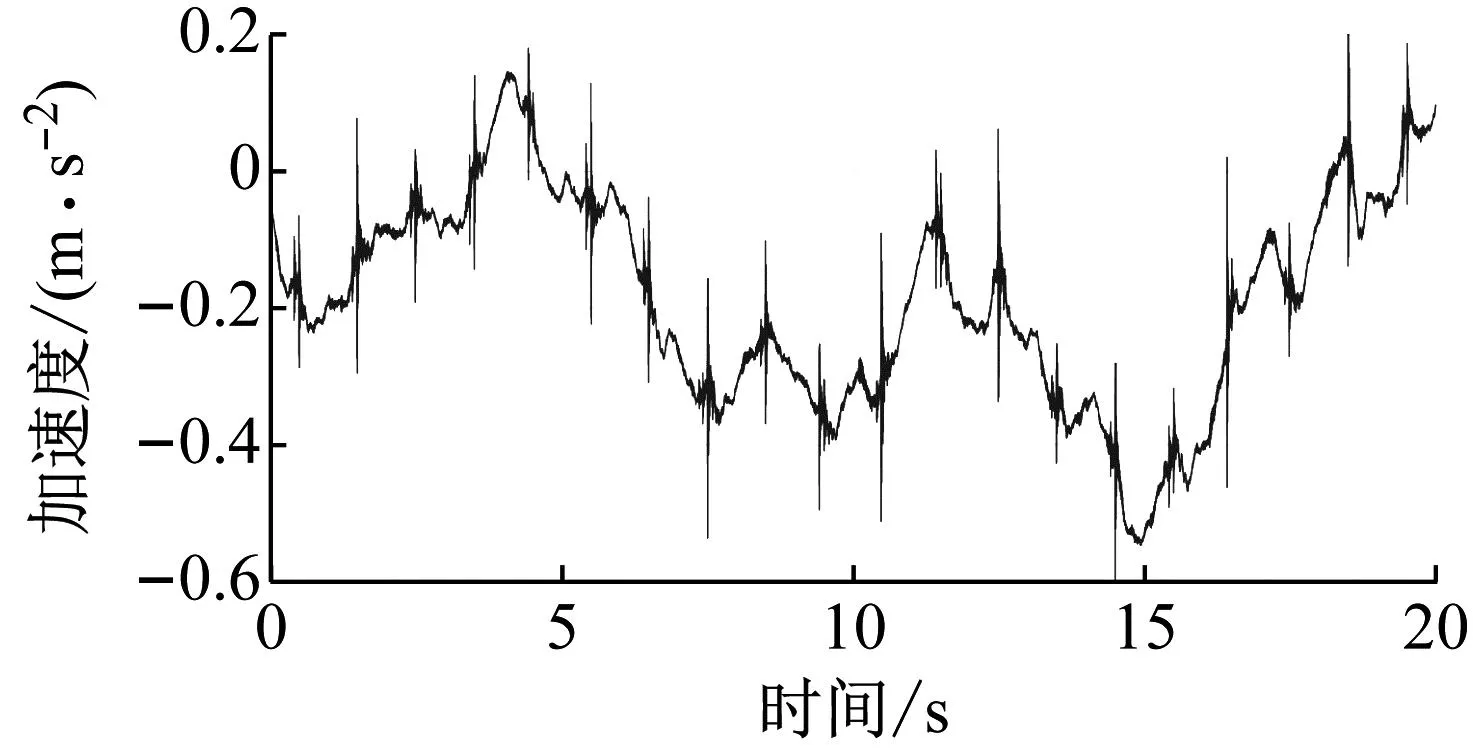
图6 在5%损伤情况下节点5处20 s的加速度信号
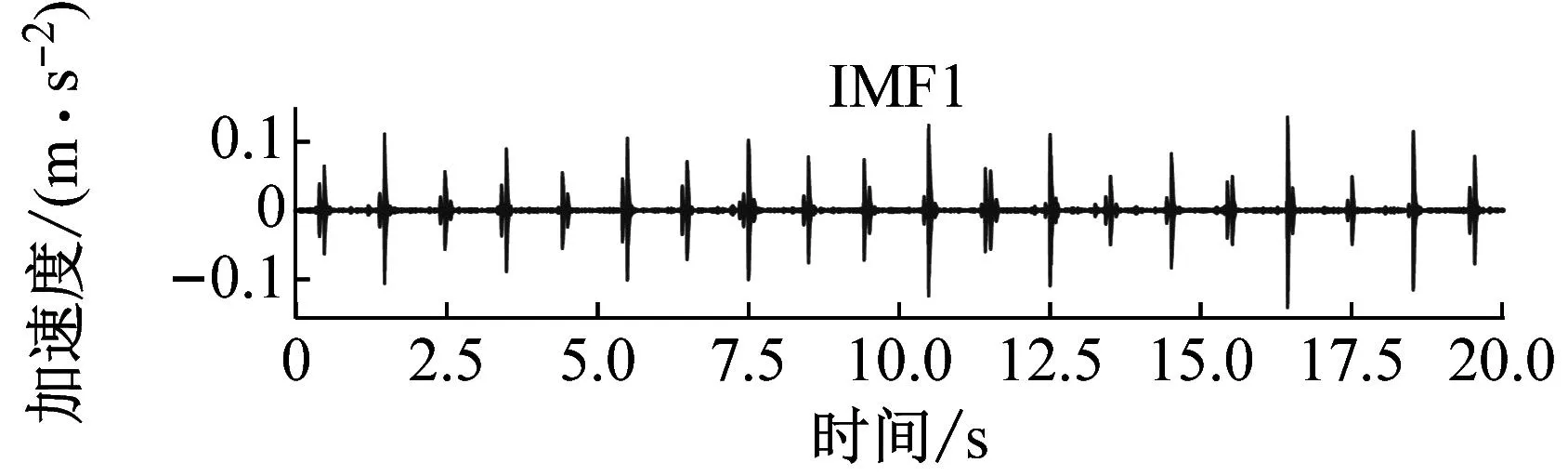
图7 IMF1~IMF4与对应的PSDs
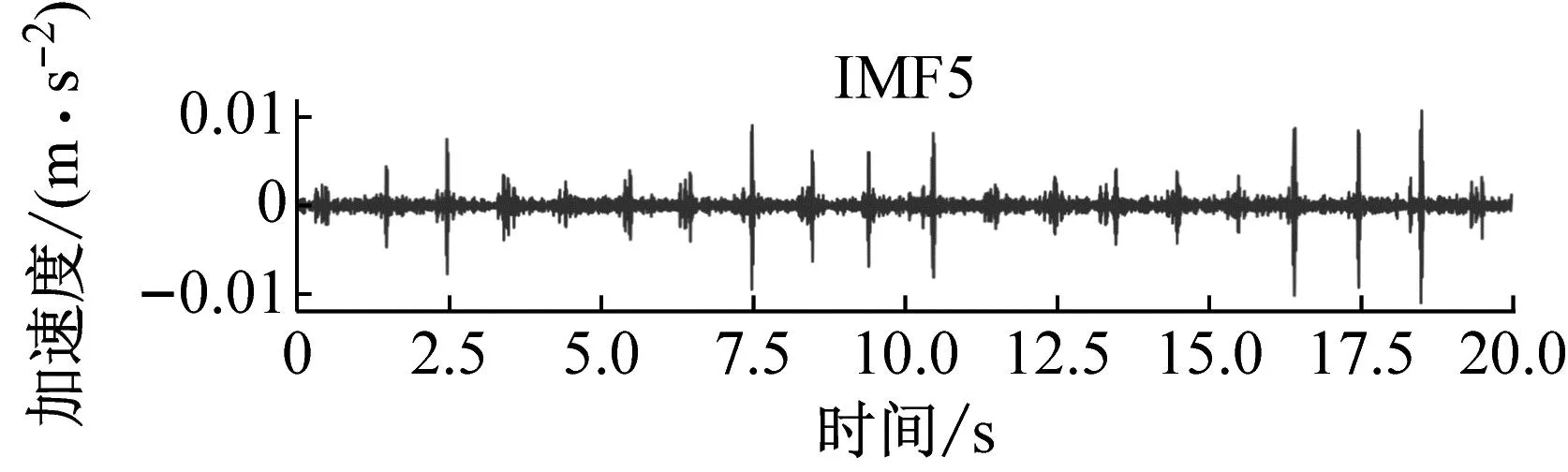
图8 IMF5~IMF8与对应的PSDs
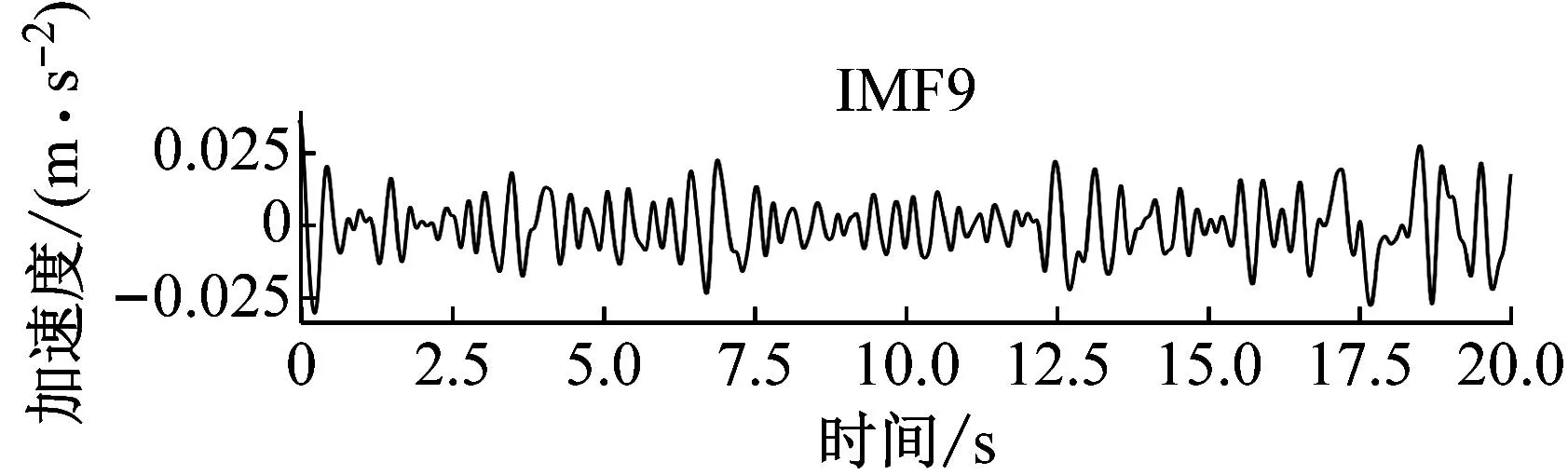
图9 IMF9~IMF12与对应的PSDs
根据图10轮廓系数结果将聚类数设为5,利用K-means++对CSD进行聚类,结果如图11所示。由图11可知,IMF1~IMF2、IMF3~IMF5、IMF6~IMF7、IMF8~IMF9、IMF10~IMF12各被分为一类。其中IMF1~IMF2为局部弯曲响应,IMF3~IMF4表示全局弯曲响应,IMF6~IMF7表示刚体动态响应,IMF8~IMF9表示准静态响应,IMF10~IMF12为显著低频信号,属于信号漂移项[43]。值得注意的是由于在中国使用的交流电频率为50 Hz,利用加速度传感器收集信号时不可避免地会受到影响,IMF5对应交流电信号。该分量由于频谱特征清晰,在研究过程中容易被误认为是有效信号加以利用,需要研究者们在信号分析时予以剔除。
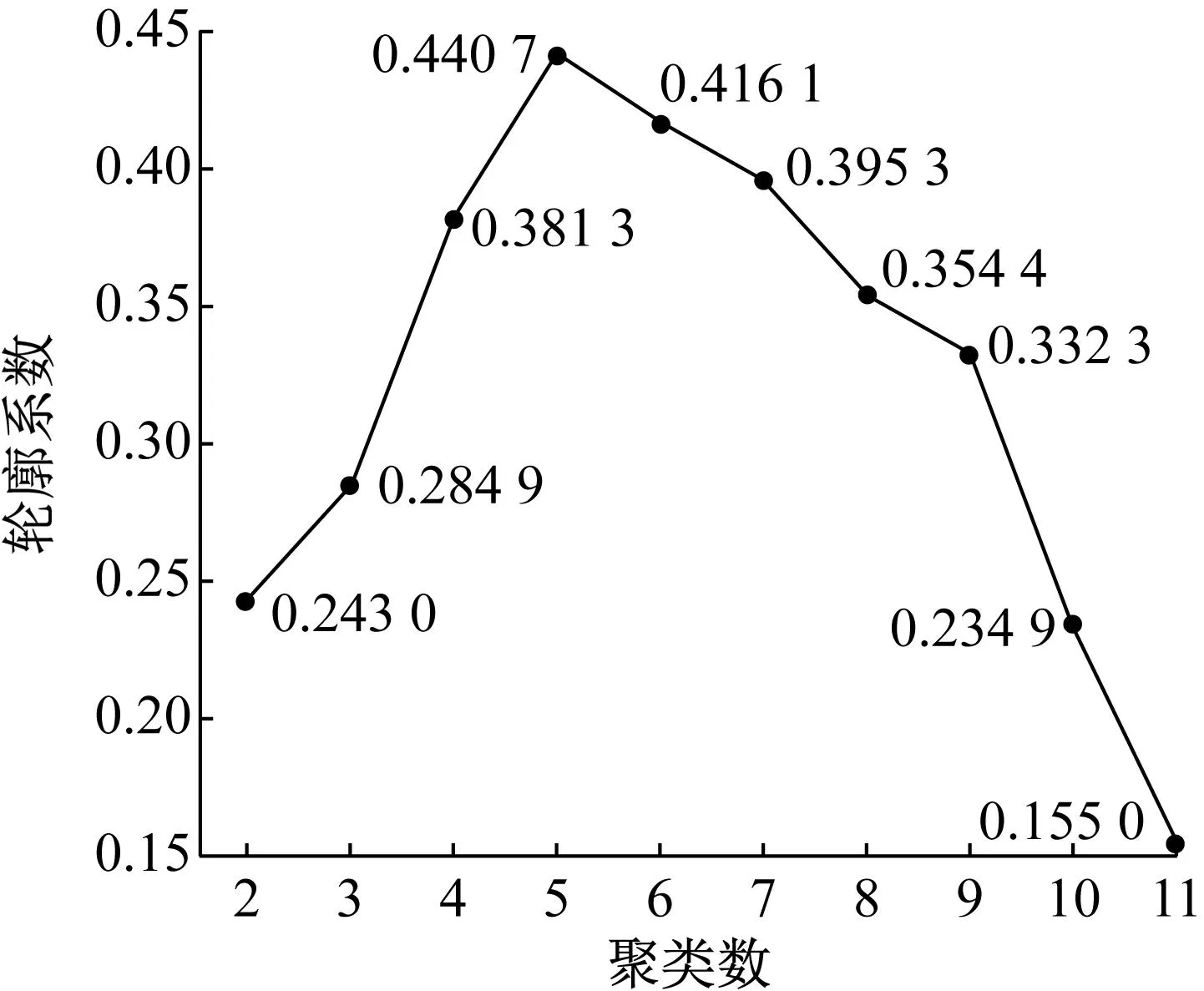
图10 不同聚类数时利用K-means++得到的轮廓系数
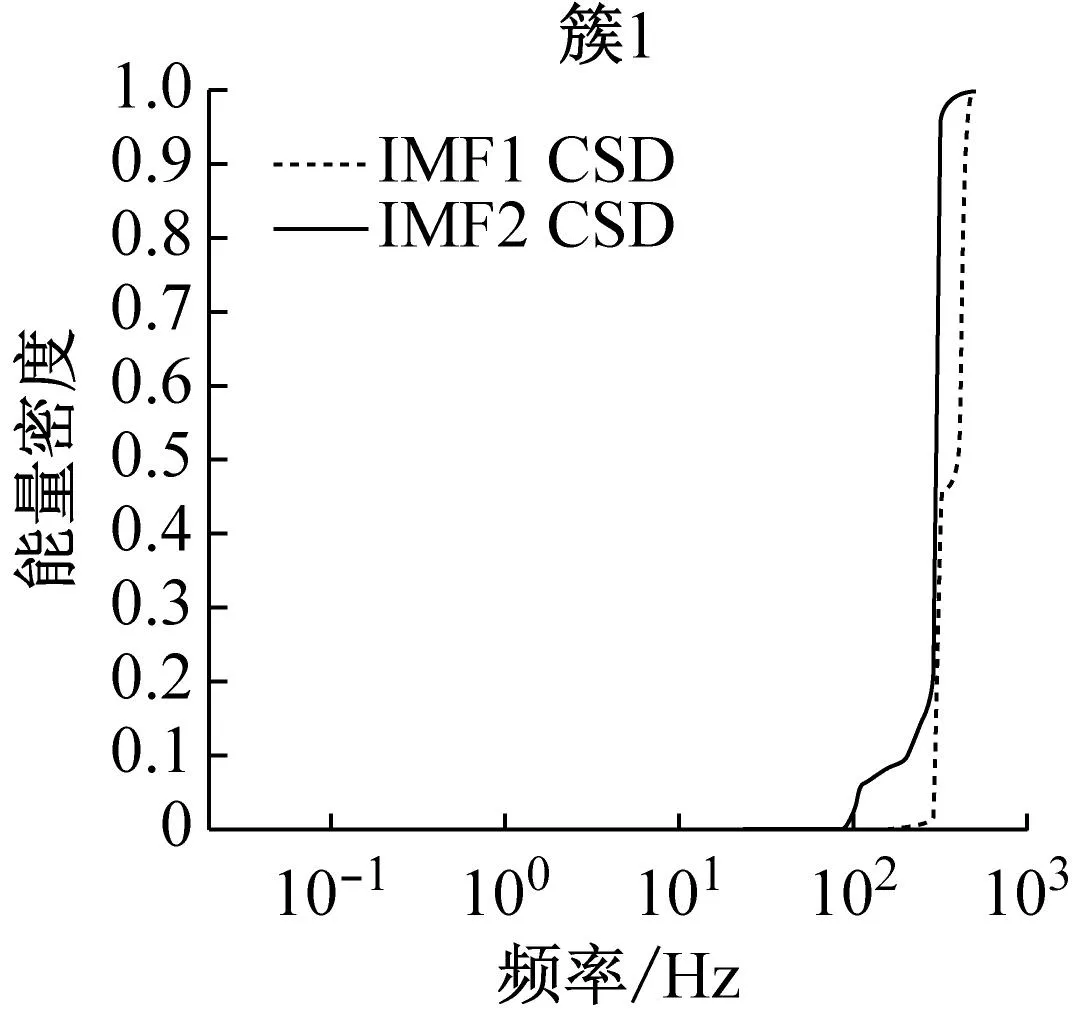
图11 利用K-means++对IMFs对应的CSDs聚类得到的结果
对IMF1~IMF2、IMF3~IMF4、IMF6~IMF7、IMF8~IMF9、IMF10~IMF12进行重构,结果如图12所示。其中图12(a)为局部弯曲响应,只在波浪到达时变化较大,包含结构局部损伤信息,是研究需要的损伤特征子信号;图12(b)表示全局弯曲响应,与局部弯曲响应有一定的相似性,其在冲击随后的较短时间内呈现出逐渐衰减的趋势,可用于识别波浪冲击;图12(c)表示刚体动态响应,图12(d)表示准静态响应,两者都没有明显冲击造成的特征;图12(e)表示基线漂移项。
(a) 局部弯曲响应
2.3 波浪激励下高桩码头桩基损伤识别
在引言部分说明了频率是目前常用的一种损伤识别方法。采用随机子空间法对健康和5%损伤情况下的动态响应数据进行处理,得到前三个频率如表2所示。
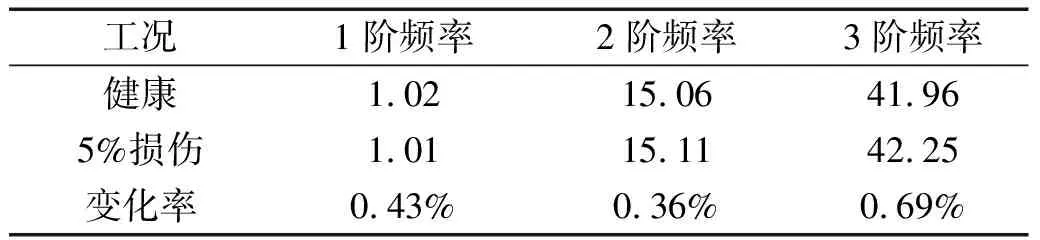
表2 损伤前后频率对比
由表2可知,一阶频率和波浪频率一致,与结构损伤无关。损伤前后的二阶和三阶频率变化不明显。这说明传统的频率法无法基于波浪激励下动力响应实现桩基损伤识别。
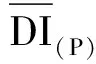
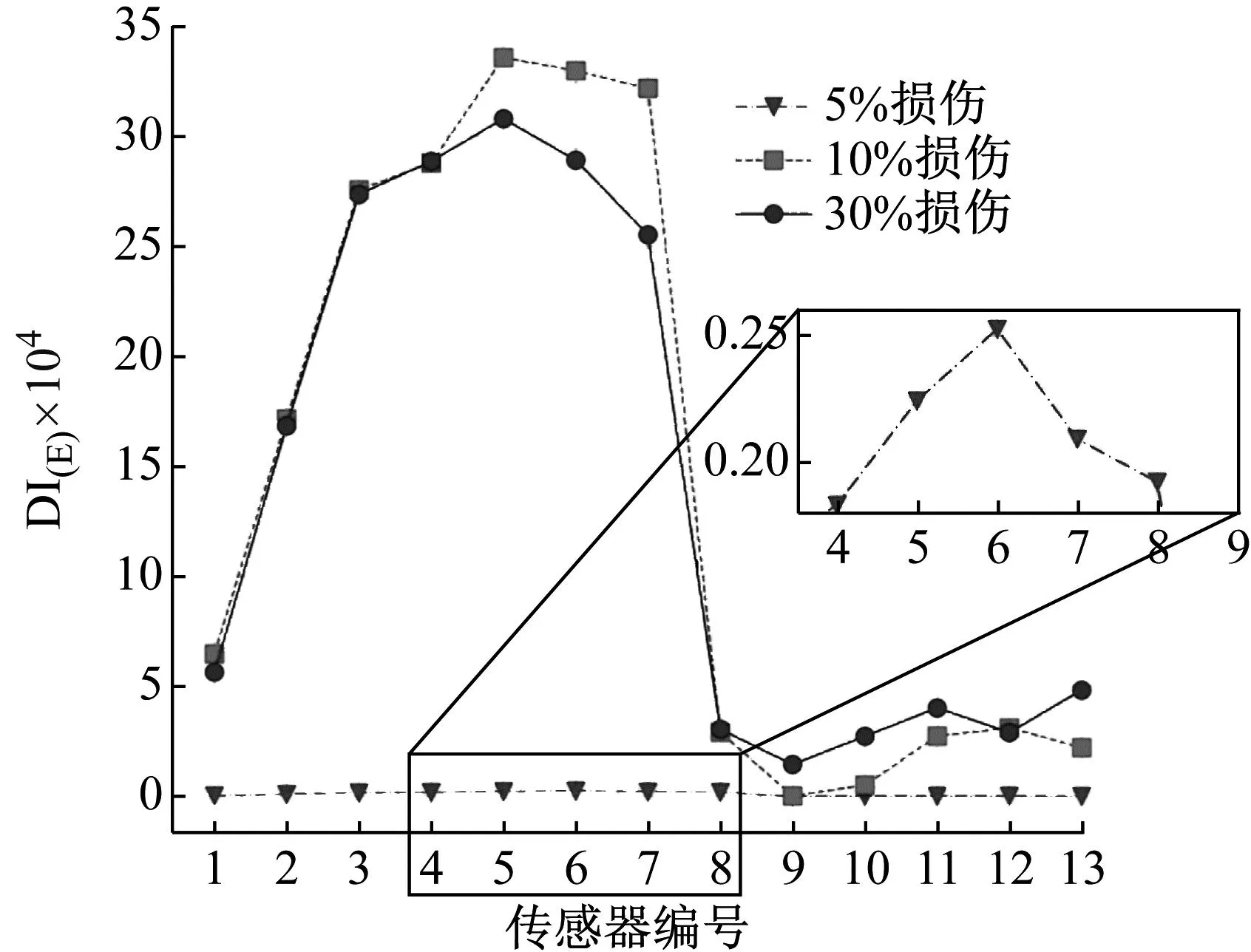
图13 在不同损伤程度下不同节点处的DI(E)
图14 在不同损伤程度下不同节点处的DI(P)
鉴于此,根据式(15)构造复合能量损伤因子DI(E,P)用于提升损伤识别效果,计算结果如图15所示。可以看出三条曲线存在显著的大小关系,即30%>10%>5%,且整体先上升后下降的趋势,其中10%损伤、30%损伤的曲线均在5号节点达到最大,5%损伤的曲线在节点6处达到最大,表明通过该指标成功识别出桩基损伤存在、损伤位置和损伤程度。
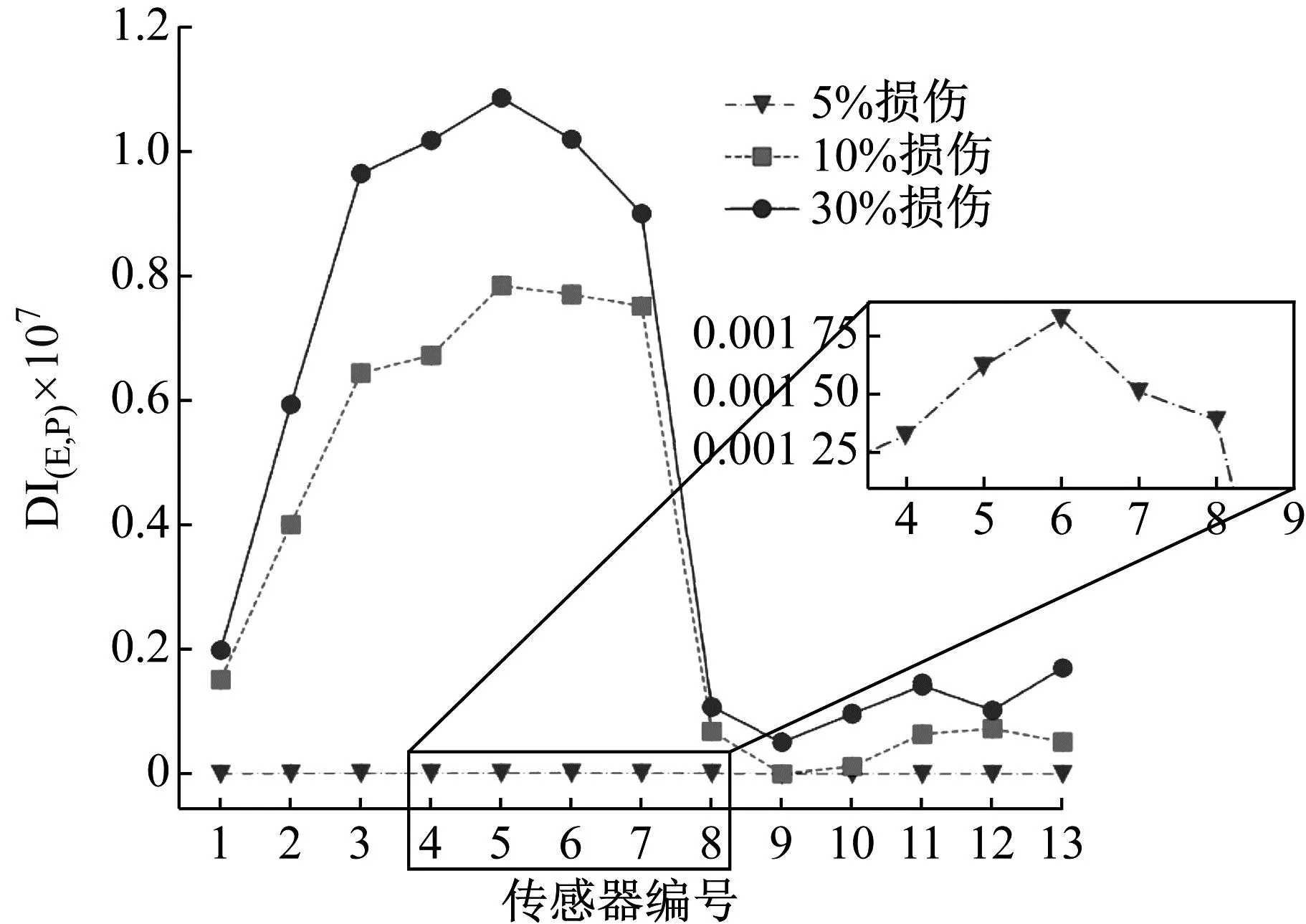
图15 在不同损伤程度下不同节点处的DI(E,P)
总结来说,根据DI(E)能够在波浪激励下准确识别桩基损伤存在与损伤位置,但对损伤程度的识别不敏感,而DI(P)能反映桩基损伤存在与损伤程度,但对损伤位置的识别不敏感;复合能量因子DI(E,P)保持了DI(E)和DI(P)的优点,能准确识别出损伤存在、损伤位置和损伤程度。不同特征、指标的损伤识别效果汇总如表3所示。
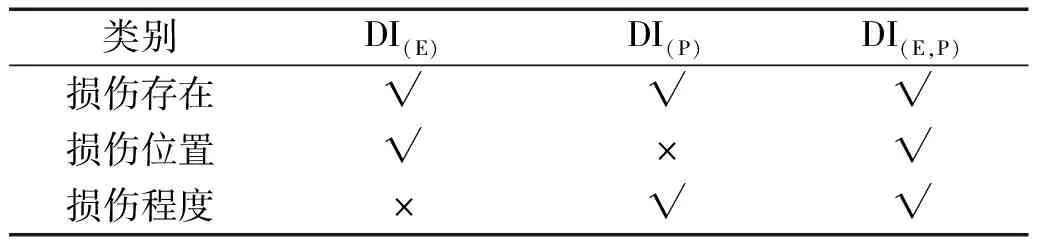
表3 不同指标的损伤识别效果
3 结 论
波浪是高桩码头桩基持续、重要外部激励来源,探索波浪激励下桩基损伤识别对于构建结构健康监测体系具有重要意义。本文提出了一套有效识别波浪激励下桩基动力响应在损伤前后特征变化的新方法。该方法针对波浪激励下桩基响应非线性、非平稳、多信号混杂等特性,结合CEEMDAN与K-means++构建自动信号分解与重构方法,从中提取损伤特征子信号。进一步针对单一特征在损伤识别效果方面的局限性,基于能量与相位提出一种新型复合能量损伤因子,以此提高对桩基损伤识别的性能。根据波浪激励下高桩码头桩基模型损伤试验,得到以下结论:
(1) 通过CEEMDAN能够克服波浪激励下桩基动力响应多类型信号混叠的问题,将其分解为若干分量,并减弱模态混叠现象;基于CSD、K-means++能够实现IMFs的自动分类与准确重构,提取代表不同信息的响应。新方法综合考虑信号的频谱离散性和集中性,能有效对复杂信号进行重构和特征提取,广泛适用于多种实际工程的动力信号分析。
(2) 基于损伤特征子信号构造的指标中,能量损伤指标DI(E)能识别出损伤位置,但对损伤程度的识别敏感程度不足;相位损伤指标DI(P)能反映桩基损伤存在和损伤程度,但对损伤位置的敏感程度不足。
(3) 传统的频率法无法基于波浪激励下动力响应实现桩基损伤识别,而复合能量因子DI(E,P)兼顾了DI(E)和DI(P)的优点,能准确识别出桩基损伤存在、损伤程度和损伤位置。
本文根据波浪激励下桩基动力响应信号提出一套由信号重构到损伤识别的新方法,为其他近海结构桩基(海上风电、跨海大桥等)动力响应分析及特征提取提供新的手段和思路。

