高速磁浮列车-轨道梁耦合系统轨道不平顺敏感波长研究
韩 艳,卜秀孟,王力东,,罗 颖,李 凯
(1.长沙理工大学 土木工程学院,长沙 410114;2.长沙理工大学 桥梁工程安全控制教育部重点实验室,长沙 410114;3.中国建筑第五工程局有限公司,长沙 410004)
高速磁浮可填补高速铁路和航空运输之间的速度空白,是下一代交通运输系统中最具发展前景的交通工具之一[1-3]。作为引起磁浮列车-轨道梁系统耦合振动的主要激励源,轨道不平顺对车辆动力学性能的影响一直是研究的重点[4]。实际的轨道不平顺是随里程变化的随机过程,可以看成由不同波长、不同幅值、不同相位的谐波叠加而成。在一定的运行速度下,不同的不平顺波长对车辆的激扰频率不同,某些波长会激发车辆的显著振动[5]。因此,明确高速磁浮列车-轨道梁系统不平顺敏感波长,可为磁浮线路不平顺管理与控制提供必要的基础数据和重要的理论依据[6]。
目前,已有学者针对轨道不平顺引起的磁浮列车(-轨道梁)系统振动响应开展研究。Long等[7]将悬浮车辆简化为单铁悬浮系统,分析了正弦型、三角型、方波型等多种长波和短波不平顺模型对系统悬浮状态的影响,发现不平顺对悬浮间隙和电流有直接影响。Zhou等以一个悬浮模块为研究对象,通过建立悬浮模块-控制系统模型,研究了轨道不平顺激励下系统的动力响应,发现某些不平顺波长和车速组合下可观察到悬浮模块的共振。余佩倡等[8]则建立了带周期性不平顺的悬浮模块-车体模型,从干扰输入和系统输出的角度探究了不平顺对悬浮系统的影响,给出了敏感波长区域并提出了抑制周期性不平顺的控制器设计方法。然而,由于这类研究重点关注悬浮系统,并未建立完整的磁浮列车-轨道梁耦合振动模型。Zhao等[9-10]较早建立了高速磁浮列车-轨道梁竖向耦合振动模型,初步探讨了轨道随机不平顺对系统动力响应的影响。Shi等[10]建立了高速磁浮-轨道梁空间耦合振动模型,分析了线路局部不平顺和随机不平顺对系统动力指标的影响,发现长波不平顺对车体竖向动力性能影响很大,但并未给出具体波长范围。Yau[11]从共振频率角度出发,对轨道和车速的关系进行了研究,指出当车速和不平顺波长激起的频率接近车轨共振频率时,将影响车辆的运行稳定性。Wang等[12]研究了高温超导磁悬浮列车-桥耦合振动响应,结果表明,轨道不平顺对车辆振动影响显著,但对桥梁影响较小。陈志贤等[13]研究了车辆悬挂系统参数及轨道不平顺对时速600 km高速磁浮列车动力学性能的影响,并基于车辆平稳性和乘坐舒适度指标给出了高、低不平顺和轨向不平顺幅值分别不超过2.8 mm和4.2 mm的建议。
上述研究以轨道不平顺幅值影响为研究重点,即使涉及波长也仅对波长范围进行了简单划分,并未给出具体的敏感波长范围。事实上,波长是评估线路平顺性的重要指标[14]。铁路线路研究经验也表明,在严格实行轨道不平顺峰值管理与均值管理基础上,还必须考虑波长对高速行车动力性能的影响[15]。蒋海波等[16]研究了线路周期性不平顺激励频率对低速磁浮列车振动响应的影响,然而该研究仅分析了两个波长激励频率。魏高恒等[17]以正弦波和轨道随机不平顺作为输入,建立了多力元模拟悬浮力的磁浮车辆竖向动力学模型,研究了不同波长的轨道竖向激励对磁浮车辆系统动力学指标的影响规律。王波等[18]建立了中低速磁悬浮列车车体振动响应与轨道不平顺的相干函数,讨论了引起车体横向和竖向振动的敏感波长,并发现磁浮列车前、后端车体振动加速度敏感波长存在差异。以上两项研究均以中低速磁浮为研究对象,且并未考虑下部轨道梁结构振动对车辆振动响应的影响。随着高速磁浮列车建设日益提上日程,明确列车-轨道梁系统敏感波长对高速磁浮系统研发与建设具有重要意义。
本文以上海高速磁浮为研究背景,建立了高速磁浮列车-轨道梁耦合系统空间精细化模型,其中磁浮列车被模拟为具有537个自由度的多体动力学模型,轨道梁被模拟为空间有限元模型,两者之间通过基于比例-微分(proportional-differentiation,PD)控制理论的磁轨关系耦合。考虑轨道竖向和横向不平顺输入为正弦波,探讨不平顺波长和幅值对系统振动响应的影响,确定设计时速下车-桥系统敏感波长范围,并从不平顺波长管理角度给出控制高速磁浮列车-桥耦合振动的相关建议。
1 磁浮列车-轨道梁空间耦合振动模型
1.1 列车子系统模型
本文采用多体动力学方法建立磁浮列车子系统模型,如图1所示。列车由n节车辆组成,每节车辆包含1个车体、4个转向架、16个摇杆、14个悬浮磁铁和14个导向磁铁,以及相邻两节车厢首、尾转向架之间的2个悬浮电磁铁和2个导向电磁铁。每个转向架由两个C形框架组成,两个C形框架通过纵向轴连接,因此两个框架可以相对旋转,但没有相对平移。每个悬浮电磁铁上安装有12个磁极,每个导向电磁铁上安装有3个导向磁极。车辆刚体之间通过线性弹簧元件或线性弹簧-阻尼器元件连接,各刚体之间的连接方式见图1(a),列车子系统参数主要参考Wang等[19]的模型。
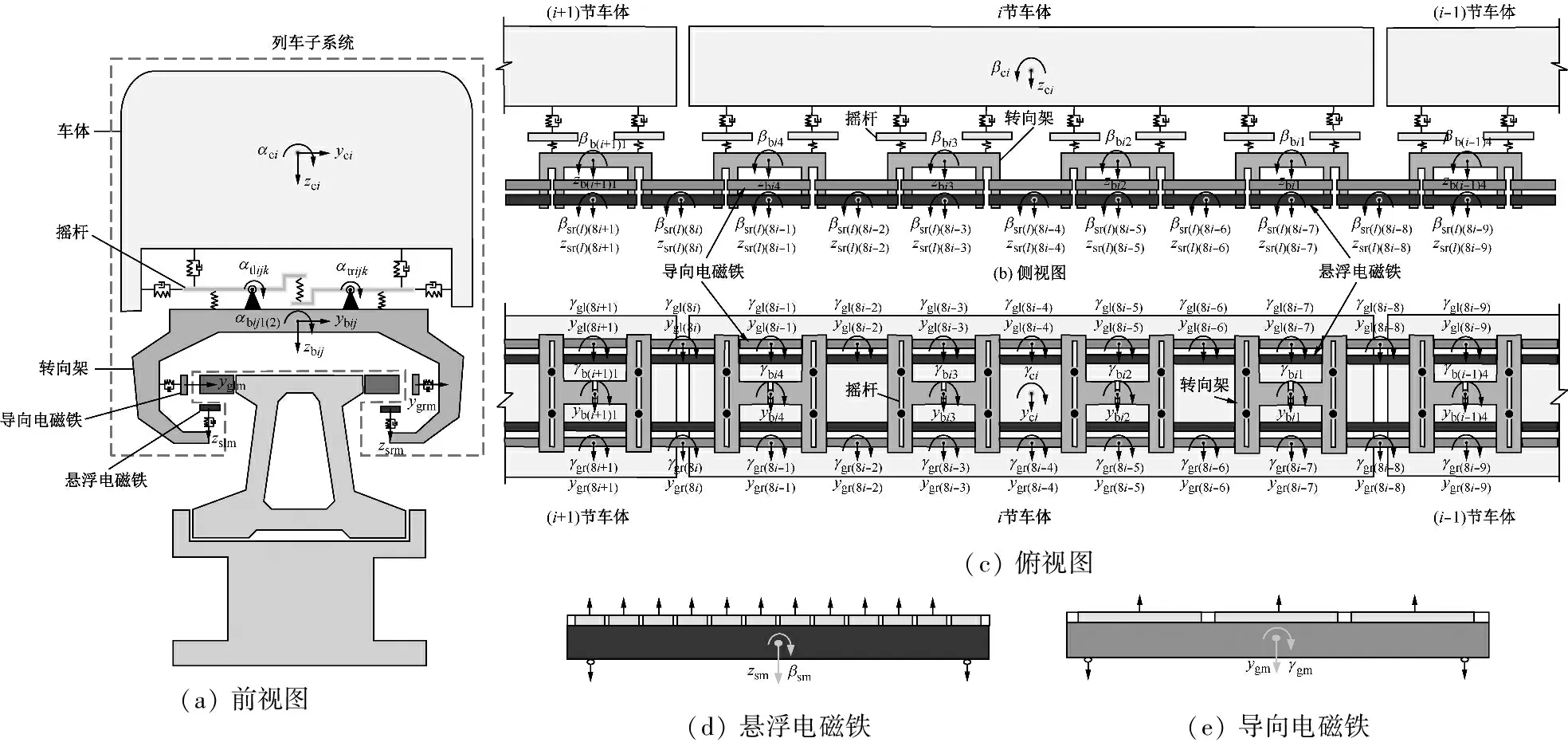
图1 列车子系统模型
在列车子系统中,车体考虑横移、沉浮、侧滚、点头和摇头5个自由度,转向架考虑自身的横移、沉浮、点头和摇头以及两个C型框架的相对转动6个自由度,摇杆只考虑侧滚1个自由度,悬浮磁铁考虑沉浮和点头2个自由度,导向磁铁考虑横移和摇头2个自由度。因此,磁浮列车子系统的总自由度数为109n-8个。
基于图1建立的列车子系统模型,根据达朗贝尔原理可建立其相应的动力方程如下
(1)
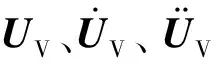

表1 列车子系统前5阶自振频率
1.2 轨道梁子系统模型
考虑磁浮列车在单线简支梁桥上运行,单跨简支梁长24.768 m。桥梁由混凝土主梁、钢制导轨和混凝土桥墩组成,钢轨位于主梁上翼缘两侧,通过多对铸铁连接件与主梁连接,桥墩与主梁之间安装支座。主梁和钢轨为箱型截面,桥墩墩底为1.8 m×1.8 m实心截面,墩顶为3.0 m×1.8 m实心截面。采用有限元方法建立桥梁模型,其中主梁、钢轨和桥墩均采用铁木辛柯梁单元模拟,钢轨与主梁之间采用刚臂连接,主梁与桥墩之间的支座采用线性弹簧阻尼单元进行模拟。同时,忽略混凝土桩基与土体之间的相互作用,将桥墩底部设置为固定约束。基于上述建模方案建立的桥梁有限元模型如图2所示,相关参数如表2所示。

表2 轨道梁子系统主要部件参数
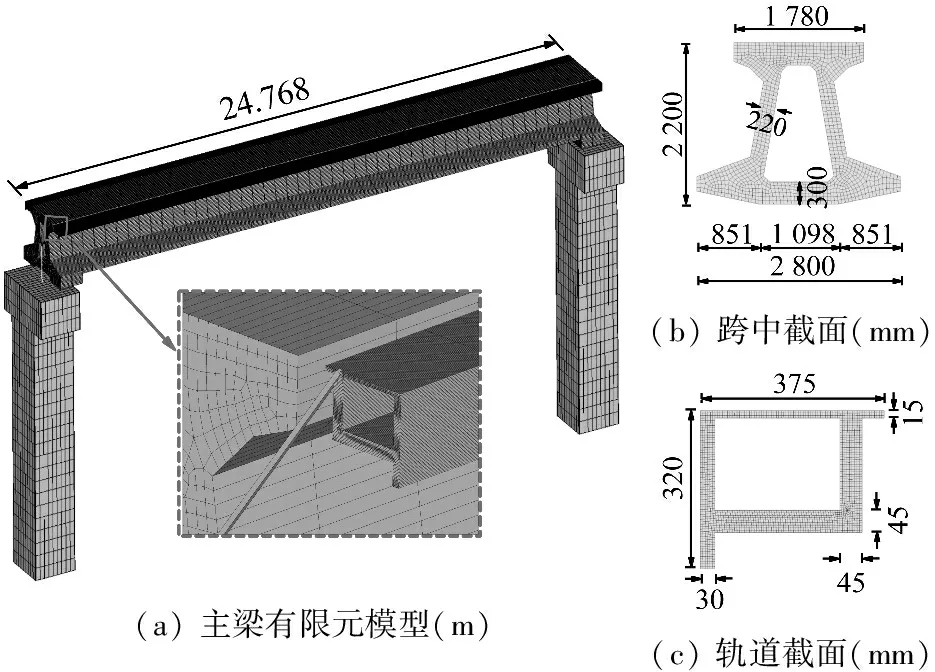
图2 桥梁有限元模型
采用直接刚度法建立轨道梁动力方程如下
(2)
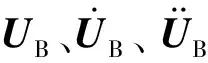
1.3 悬浮控制器模型
由于磁悬浮系统是一个先天开环不稳定的系统,故需引入控制器来维持车辆和轨道梁之间的磁浮间隙[20]。磁浮列车是一个多电磁铁悬浮系统,通过解耦,磁浮列车的悬浮控制可以分解为单个电磁铁的悬浮控制问题[21-22]。单磁铁悬浮系统的结构图,如图3所示。电磁力模型参数如表3所示。

表3 电磁力模型参数表
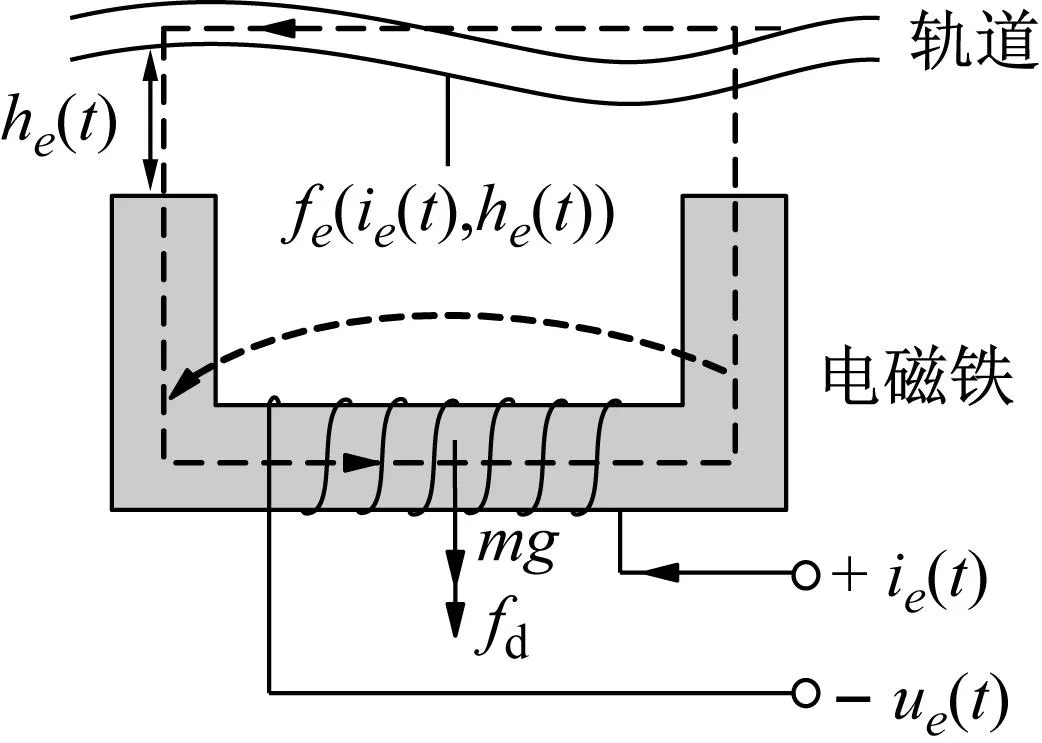
图3 单电磁铁模型
电磁力的计算主要取决于回路电流和电磁铁与轨道之间的间隙,计算公式如下
(3)
式中:fe为电磁力;ie为所计算磁极位置处线圈电流值;he为所计算磁极处的磁浮间隙;e为磁极编号;t为磁浮列车运行时间。ie,he与磁极编号e和时间t有关。
电磁铁在垂直方向上的动力方程为
(4)
式中:fd为施加在电磁铁上的外力;g为重力加速度。将式(4)在平衡点(i0,h0)附近进行泰勒级数展开(令fd=0)并忽略高阶项得到
(5)
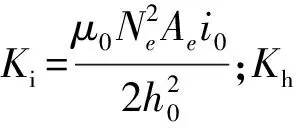
本文采用工业上常用的PD控制器通过直接调节电流达到控制电磁力的目的,即:
(6)
式中,KP和KD为比例增益系数和微分增益系数,其取值方法主要参考文献[23]。该控制算法简单,可以避免电流环带来的延迟影响,提高了系统的动态性能。
1.4 轨道不平顺模型
受轨道表面粗糙度、施工误差、桥墩沉降、自然环境变化等因素影响,磁浮轨道会产生竖向和横向不平顺[24]。轨道不平顺是随里程变化的随机过程,其幅值和波长的统计特征一般通过功率谱密度函数(power spectral density,PSD)来描述,具体计算时亦可通过PSD生成不平顺样本[25]。本文为直接建立不平顺波长与动力响应之间的关系,假设横向和竖向不平顺为正弦函数,即:
(7)
式中:A0为谐波不平顺幅值;x为距离轨道起始点的距离;v为列车行驶速度;λ为不平顺波长。
2 磁浮列车-轨道梁耦合振动方程及求解
当磁浮列车在轨道梁上运行时,列车子系统和轨道梁之间会发生动力相互作用,因此可建立磁浮列车-轨道梁耦合振动方程如下
(8)
式中:下标为“VB”或“BV”的矩阵代表由动力相互作用引起的项;FV和FB为由轨道不平顺引起的列车子系统和轨道梁子系统外荷载向量。
式(8)为耦合时变方程,本文采用分离迭代法求解。电磁力中的磁间隙由列车和轨道梁之间的运动状态和初始磁间隙决定,电磁力求解中的电流由PD控制器控制调节,从而调节电磁力。采用Newmark-β法计算桥梁和车辆的动力响应,并迭代至要求精度。整个磁浮列车-轨道梁耦合作用的计算流程,如图4所示。
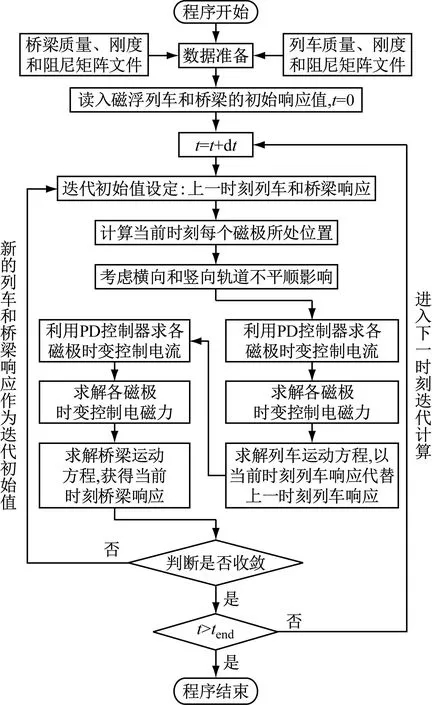
图4 动力分析流程图
3 模型验证
以上海高速磁浮线为背景,通过与实测结果对比验证本文计算模型的正确性。验证所用磁浮列车采用5节车编组,桥梁跨数考虑20跨。轨道竖向和横向不平顺样本如图5所示,它们是根据文献[26]拟合的七参数PSD函数采用三角级数叠加法模拟而成的。其中,竖向和横向不平顺幅值分别为2.09 mm和3.28 mm。采用第2章所述方法计算耦合系统动力响应,时间步长取1×10-4s。
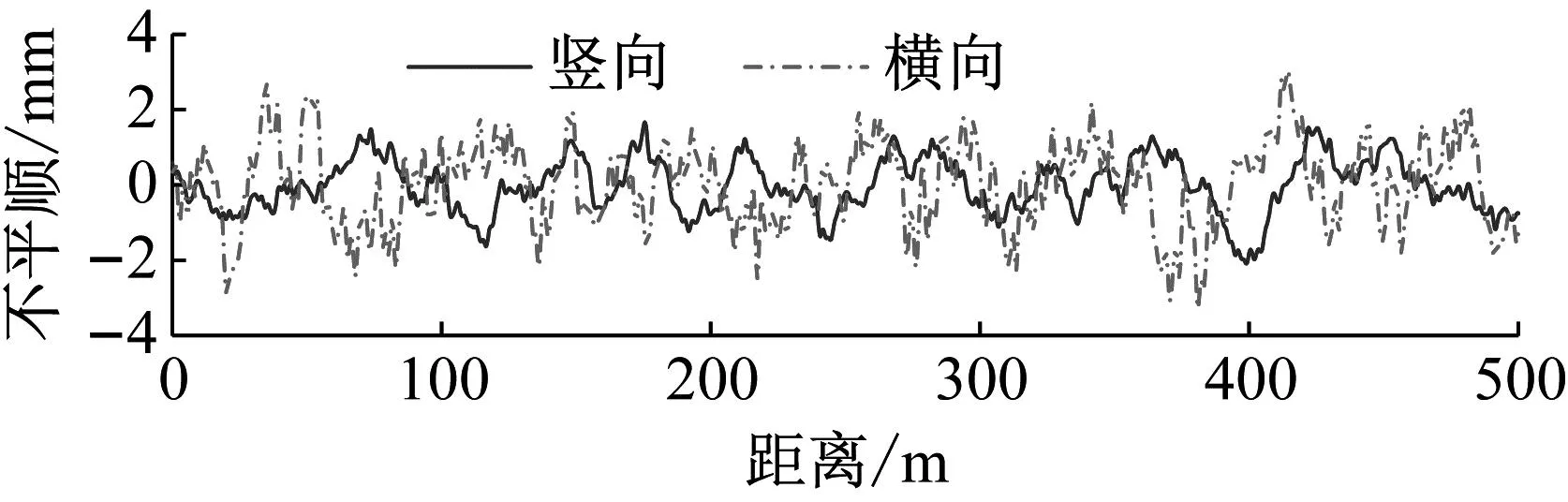
图5 轨道不平顺样本
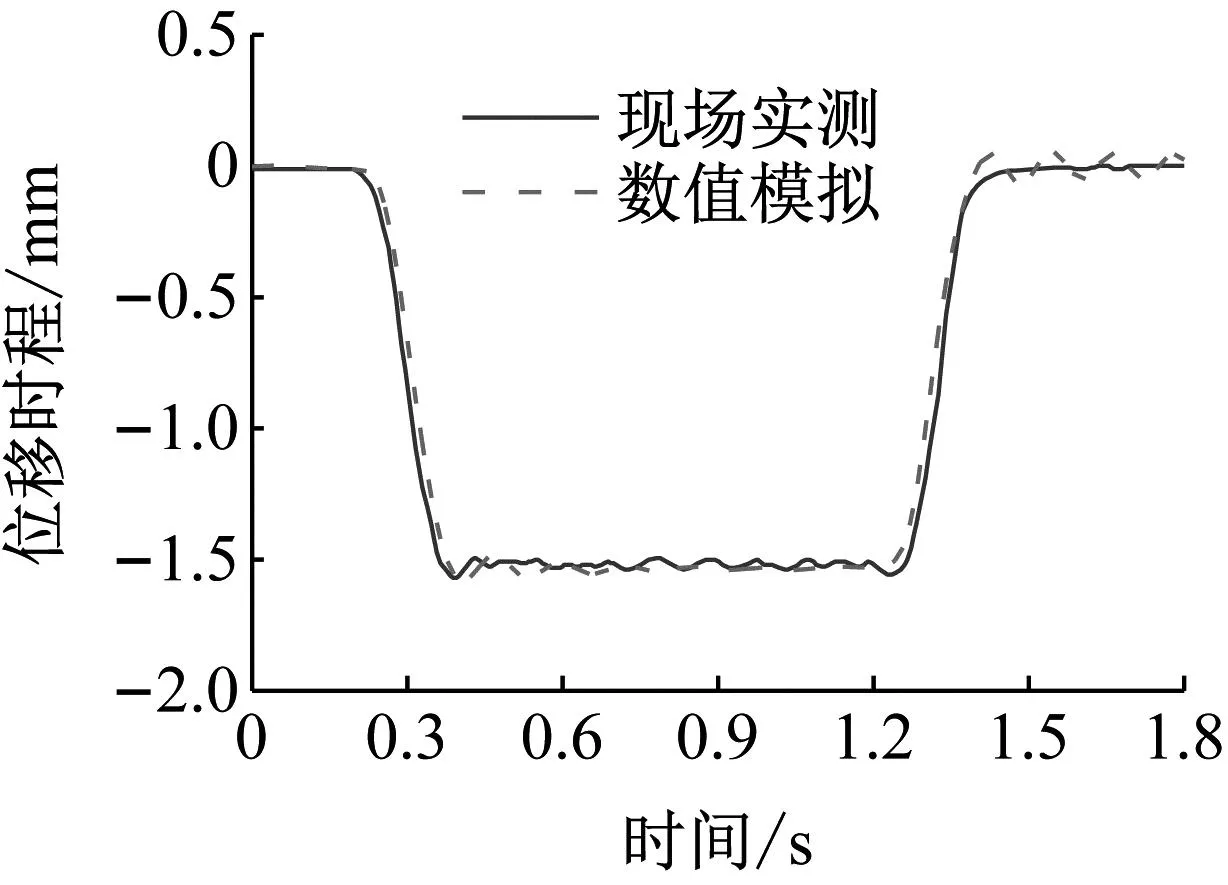
(a) 跨中竖向位移(v=430 km/h)
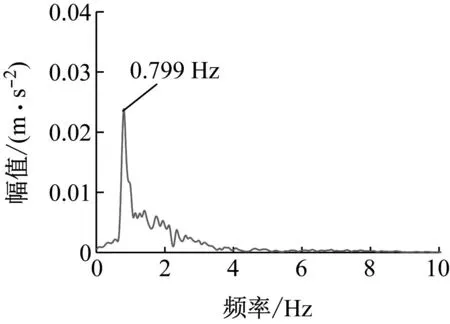
图7 列车竖向加速度谱分析
4 车-桥系统动力响应轨道不平顺敏感波长分析
本章以5节车编组磁浮列车通过20跨简支梁桥为计算背景,分析不同波长和幅值轨道不平顺对磁浮列车-轨道梁系统动力响应的影响。其中,不平顺波长范围取5~200 m,以5 m为间隔;幅值范围取1~5 mm,以1 mm为间隔。另外,值得说明的是,以下分析中车体特指第1节车车体,桥梁跨中特指第10跨主梁跨中。
4.1 车辆动力响应分析
4.1.1 不同方向轨道不平顺组合
不同方向轨道不平顺组合分为仅考虑横向轨道不平顺(以下称“横向”)、仅考虑竖向轨道不平顺(以下称“竖向”)和同时考虑横向和竖向轨道不平顺(以下称“横向+竖向”)三种情况。考虑车速为430 km/h,轨道不平顺幅值为1 mm,图8给出了不同方向轨道不平顺激励下车体加速度最大值随不平顺波长变化规律。由图8可知,车体横向、侧滚和摇头加速度主要受横向不平顺影响,竖向不平顺对其影响较小。车体竖向和点头加速度主要受竖向不平顺影响,横向不平顺对其影响较小。由此可知,磁浮列车横向振动和竖向振动的耦合性较弱。
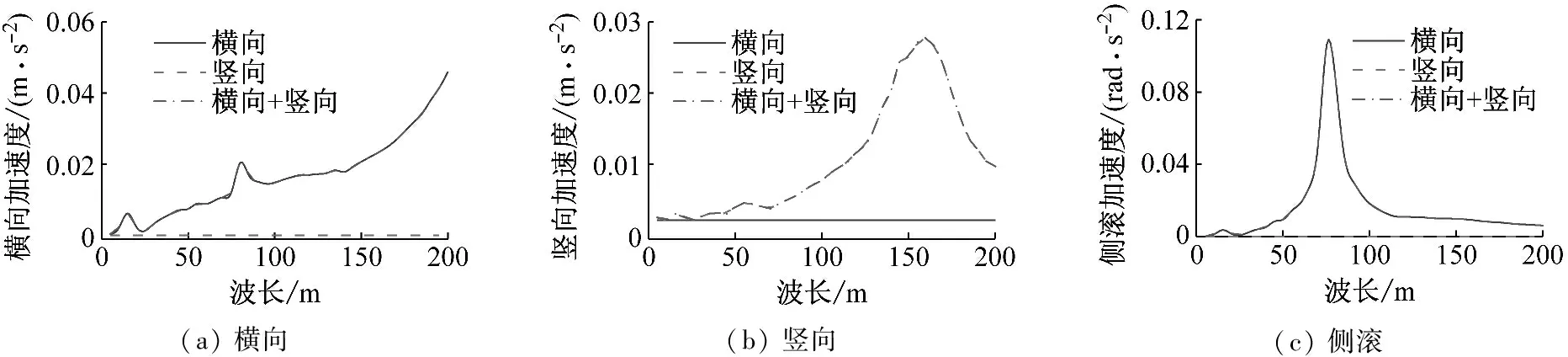
图8 不同方向轨道不平顺组合下车体加速度最大值随不平顺波长变化规律
由图8(a)和图8(e)可知,在5~200 m不平顺波长范围内,车体横向和摇头加速度变化曲线并没有出现峰值。为找出车速430 km/h时影响车体横向和摇头加速度的不平顺最不利波长,可以根据激励频率与车速和波长的关系f=v/λ,先分析低车速情况下影响车体加速度的最不利波长,再反推高车速情况下的加速度最不利波长。图9给出了车速200 km/h时车体横向和摇头加速度最大值随波长变化规律。由图9可知,当车体横向加速度峰值对应的波长为115 m时,摇头加速度峰值点对应的波长为105 m。图10分别给出了波长115 m和105 m时车体横向加速度和摇头加速度的时程曲线及幅值谱曲线。由图10(c)和图10(d)可知,横向和摇头加速度主频分别是0.47 Hz和0.52 Hz,该频率与轨道不平顺激励频率(0.48 Hz和0.53 Hz)相接近。由式(5)和(6)可知,控制参数KP的引入会改变单电磁铁模型的系统刚度,进而对整个车辆系统的刚度也会产生影响。本文中,导向控制参数KP改变了车体的横向和摇头刚度,使得车体横向和摇头自振频率发生了改变,此时车体的横向和摇头自振频率分别为0.47 Hz和0.52 Hz。因此,由图10(a)和图10(b)可知,当波长为115 m和105 m时,会分别引发车体横向和摇头方向的共振,从而使车体摇头和横向加速度的幅值迅速增大。根据车速200 km/h下车体横向和摇头加速度的最不利波长,可以反推出车速430 km/h时车体相应加速度的最不利波长分别为254 m和229 m。
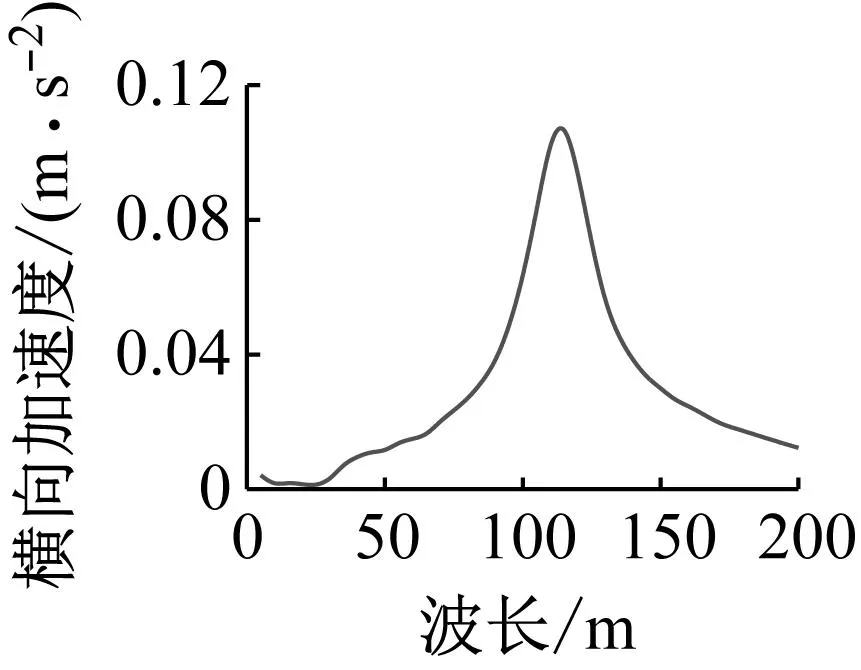
(a) 横向
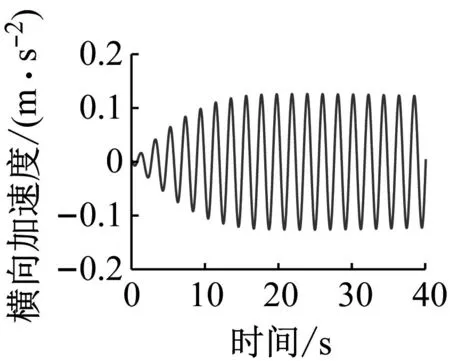
(a) 横向加速度时程
此外,从图8(a)亦可发现,在波长80 m位置横向加速度存在一个较小峰值,同时图8(c)中波长80 m附近侧滚加速度也存在峰值。为便于分析,图11给出了80 m波长下的车体横向和侧滚加速度时程及其幅值谱曲线。由图11可知,两种振动加速度对应的主频均为1.50 Hz。由于该频率与车体侧滚自振频率(1.31 Hz)接近,可以得出,波长为80 m时会引发车体侧滚方向的共振,从而导致了车体横向和侧滚振动加剧。
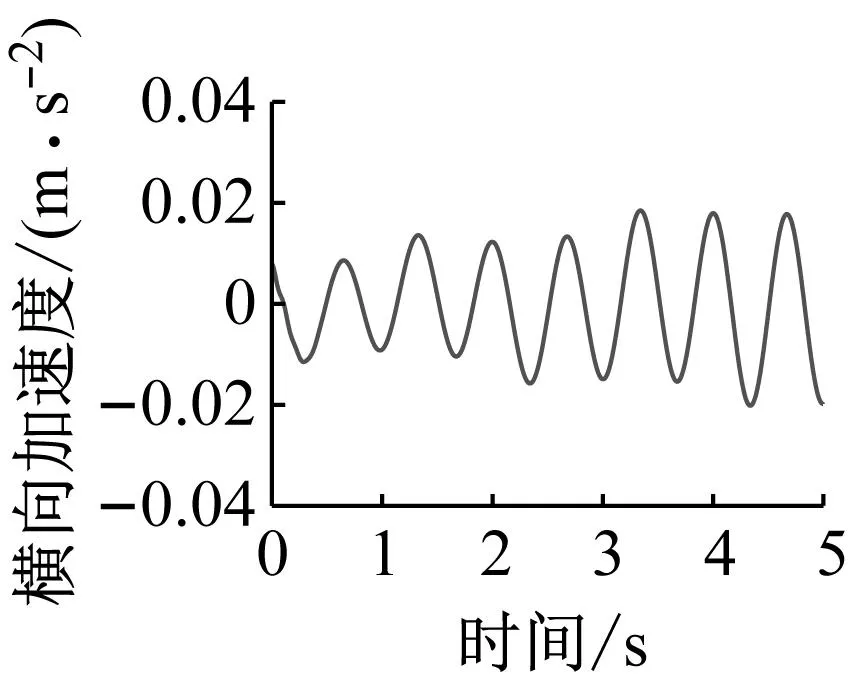
(a) 横向加速度时程
在本文中,取峰值点波长前后20 m为车体加速度敏感波长范围。因此,可以得出,当车速为430 km/h时,横向和摇头加速度敏感波长均大于200 m,车体侧滚加速度敏感波长为60~100 m。
(1)算法针对的是多站多外辐射源场景,对于单站多外辐射源场景和多站单外辐射源场景同样适用,具有较高的通用性.
由图8(b)可以看出,车体竖向加速度峰值对应的波长为160 m,点头加速度峰值对应的波长为140 m。
波长160 m时的车体竖向加速度幅值谱曲线和波长140 m时车体点头加速度幅值谱曲线,如图12所示。由图12可知,车体竖向和点头振动的主频分别为0.75 Hz和0.87 Hz。这是因为,当不平顺波长为160 m和140 m时,对应的不平顺激励频率分别为0.75 Hz和0.85 Hz。同时,这两个激励频率分别与车体竖向自振频率(0.78 Hz)和点头自振频率(0.83 Hz)十分接近。因此,可以得出,当波长为160 m和140 m时,分别引发了车体竖向和点头方向的共振,从而导致了车体竖向和点头加速度幅值的迅速增大。同样,取峰值点波长前后20 m为车体加速度敏感波长范围。可以得出竖向加速度敏感波长为140~180 m,点头加速度敏感波长为120~160 m。
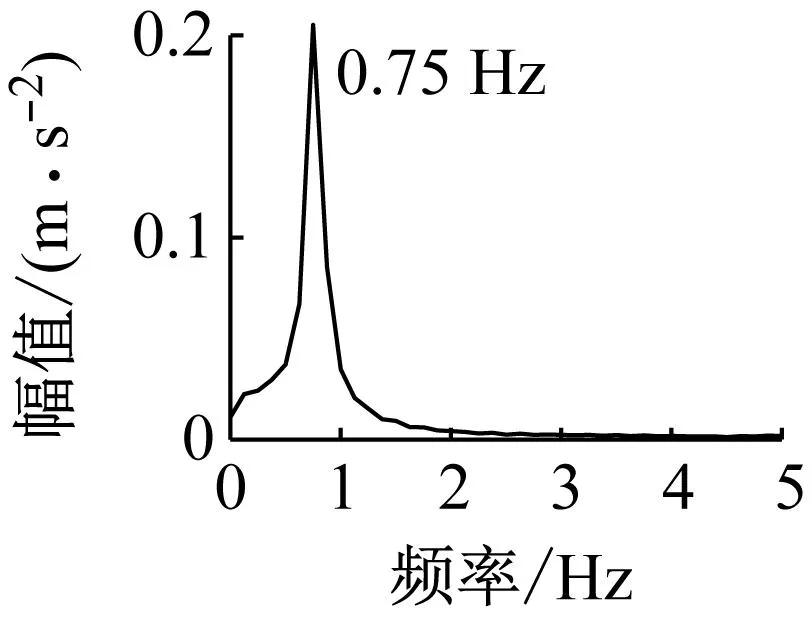
(a) 竖向
4.1.2 不同轨道不平顺幅值
车体加速度随轨道不平顺幅值和波长的变化规律,如图13所示。由图13可知,车体加速度幅值随着轨道不平顺幅值的增加而增加。同一波长下,车体加速度最大值与轨道不平顺幅值之间基本呈线性变化规律,车体加速度敏感波长随幅值的增加基本没变化。
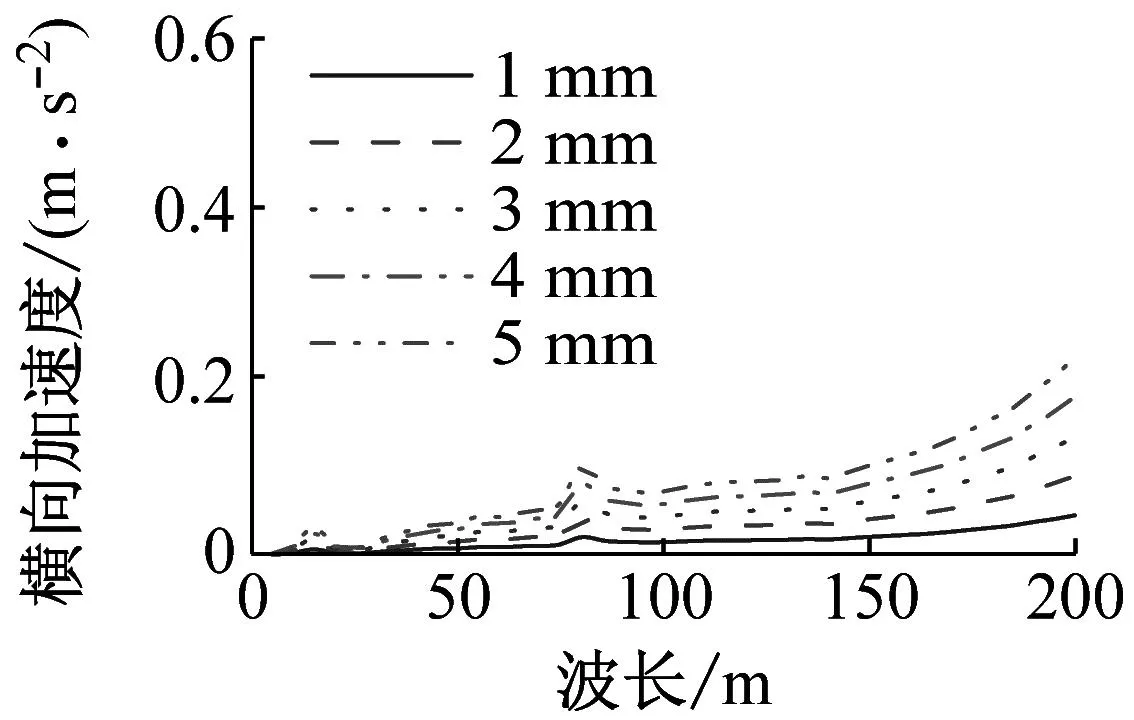
(a) 横向
4.1.3 不同车速
考虑列车以200、250、300、350、390和430 km/h等六种车速通过桥梁,轨道不平顺幅值为1 mm,探讨不同车速下车辆振动轨道不平顺敏感波长。车体加速度最大值随车速和波长的变化规律,如图14所示。由图14可知,在计算车速工况下,侧滚加速度变化曲线的峰值随车速变化不大,竖向、侧滚、点头和摇头加速度变化曲线的峰值随着车速的增大而减小。
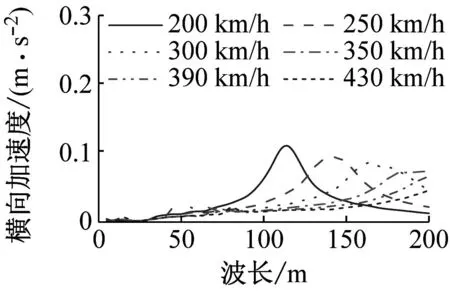
(a) 横向
不同方向的轨道不平顺组合、不同轨道不平顺幅值和不同车速情况下车体加速度的敏感波长范围,如表4~6所示。

表4 不同轨道不平顺组合下车体加速度敏感波长

表5 不同轨道不平顺幅值下车体加速度敏感波长
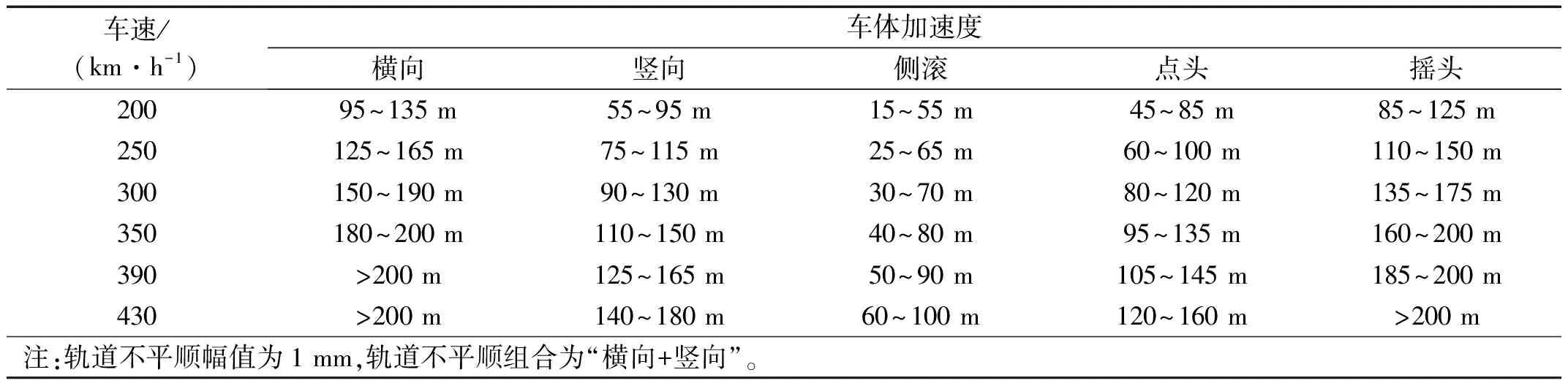
表6 不同车速下车体加速度敏感波长
4.2 桥梁动力响应分析
4.2.1 不同轨道不平顺组合
图15和图16给出了三种轨道不平顺组合下桥梁跨中横向和竖向位移及加速度最大值随不平顺波长变化规律。由图15和16可知,与车辆振动相同的结论,即桥梁横向振动和竖向振动的耦合性不强。从图15可以看出,虽然不同波长轨道不平顺激励下桥梁跨中横向振动幅值有所差异,但总体而言桥梁横向振动响应较小。从图16可以看出,不同波长轨道不平顺激励下,桥梁跨中竖向位移变化较小,但竖向加速度变化较大,两者在波长15 m的位置存在峰值。为便于分析,图17给出了15 m和100 m两种波长下桥梁跨中的竖向位移和加速度时程曲线。从图17可以看出,当车-桥系统受15 m波长轨道不平顺激励时,车辆驶入桥梁时具有更显著的振动响应。这是因为,该波长对应的激励频率(7.96 Hz)与桥梁一阶竖向自振频率(7.85 Hz)接近。但值得注意的是,由于磁浮列车-桥系统阻尼较大,该振动响应很快得到了衰减。
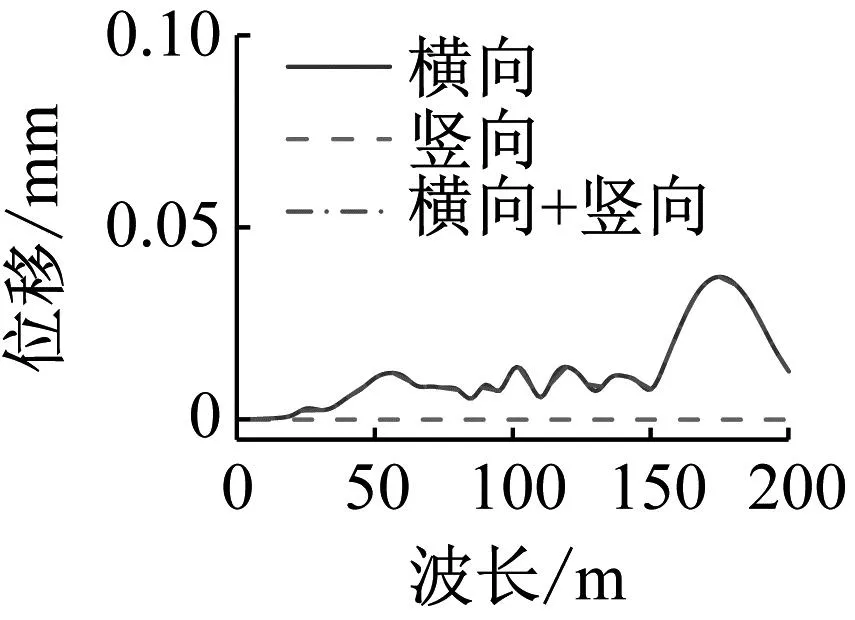
(a) 位移
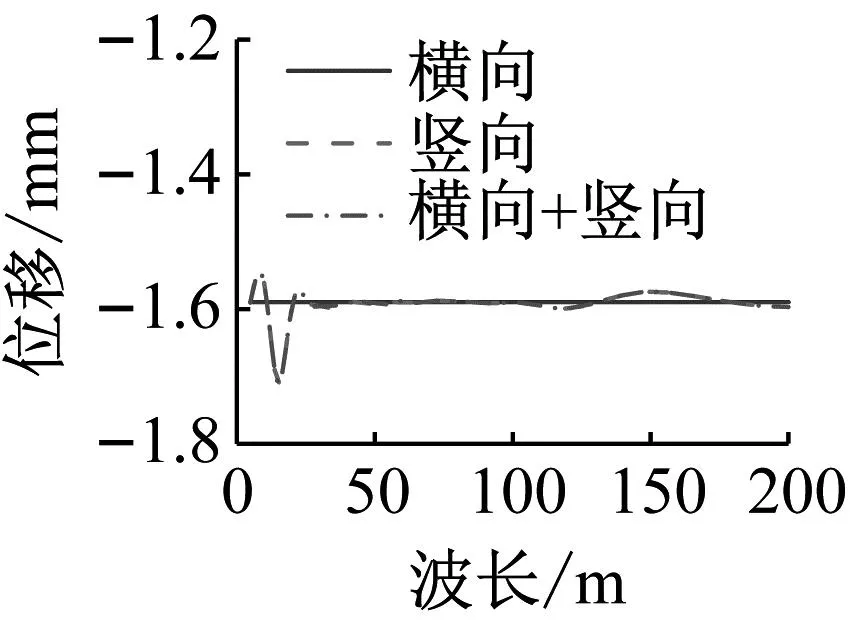
(a) 位移
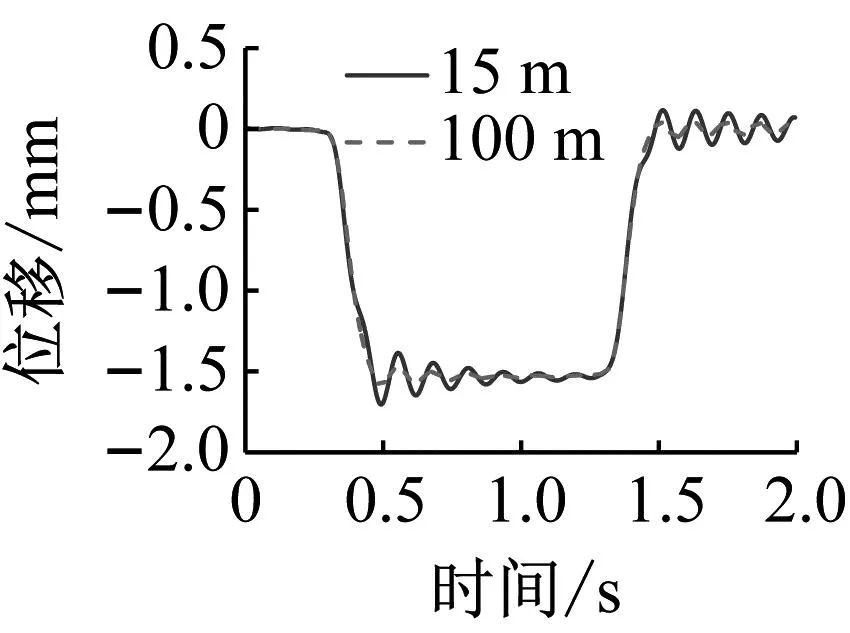
(a) 位移
4.2.2 不同轨道不平顺幅值
图18和图19给出了桥梁跨中横向和竖向位移及加速度最大值随轨道不平顺幅值和波长的变化规律。由图18和19可知,增大轨道不平顺幅值并不会影响桥梁动力响应敏感波长,但桥梁动力响应幅值随不平顺幅值的增大而增大。相同波长不平顺激励下,桥梁位移、加速度幅值最大值与轨道不平顺幅值之间基本呈线性关系。
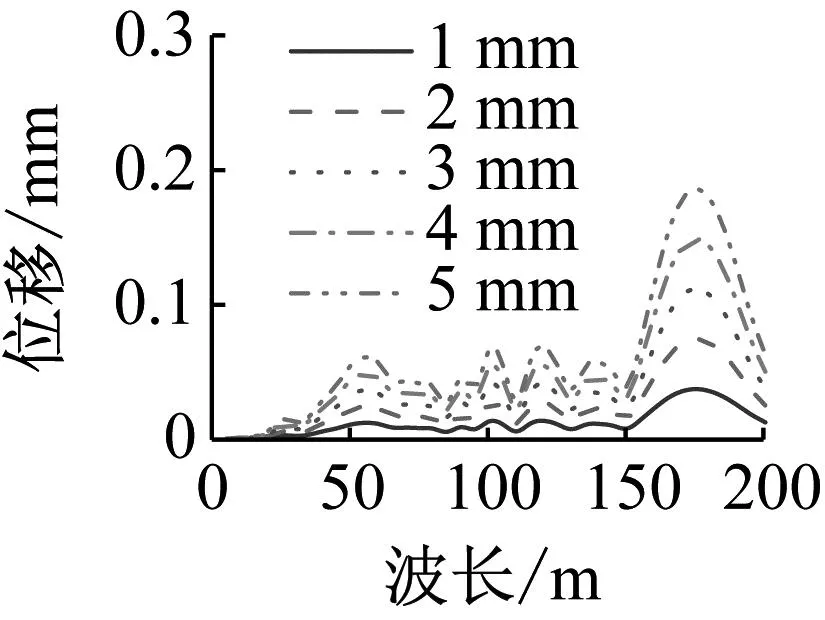
(a) 位移
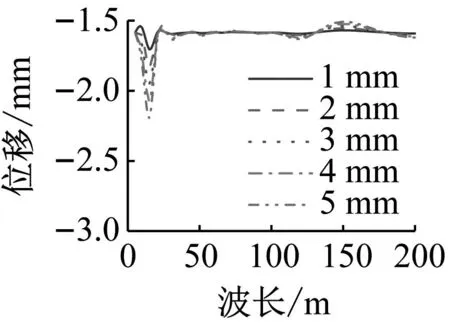
(a) 位移
4.2.3 不同车速
图20和图21给出了不同车速下桥梁跨中横向和竖向位移及加速度最大值随波长变化规律,车速范围设定与4.1节一致。由图20可知,计算波长范围内,桥梁横向位移和加速度峰值随车速变化较小,且相同波长轨道不平顺激励下,振动幅值并非随车速增大而增大。由图21可知,同一波长轨道不平顺激励下,桥梁竖向振动幅值基本呈随车速增大而增大,且竖向加速度幅值随速度增大而呈线性增大。
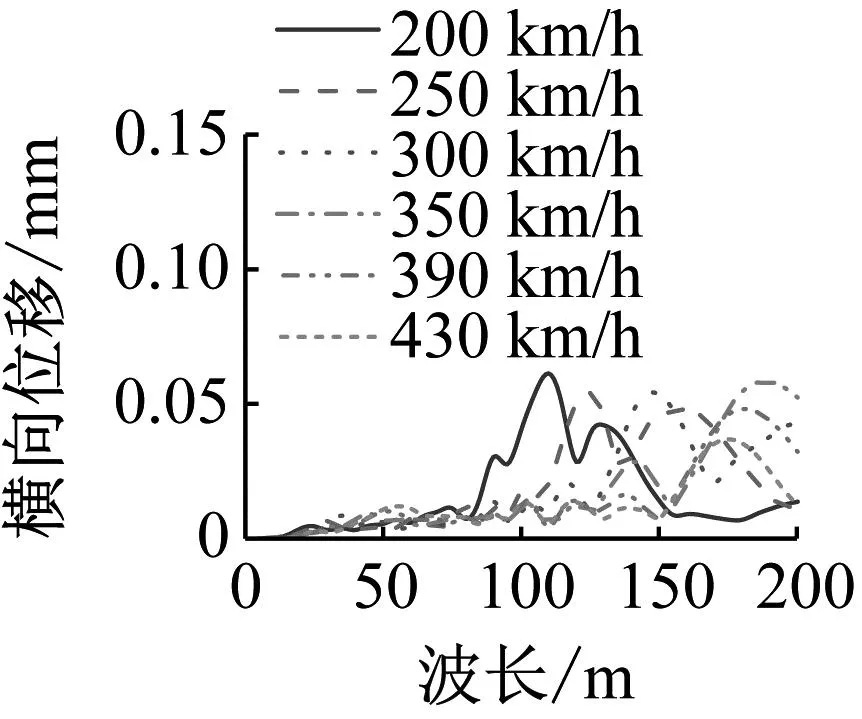
(a) 位移
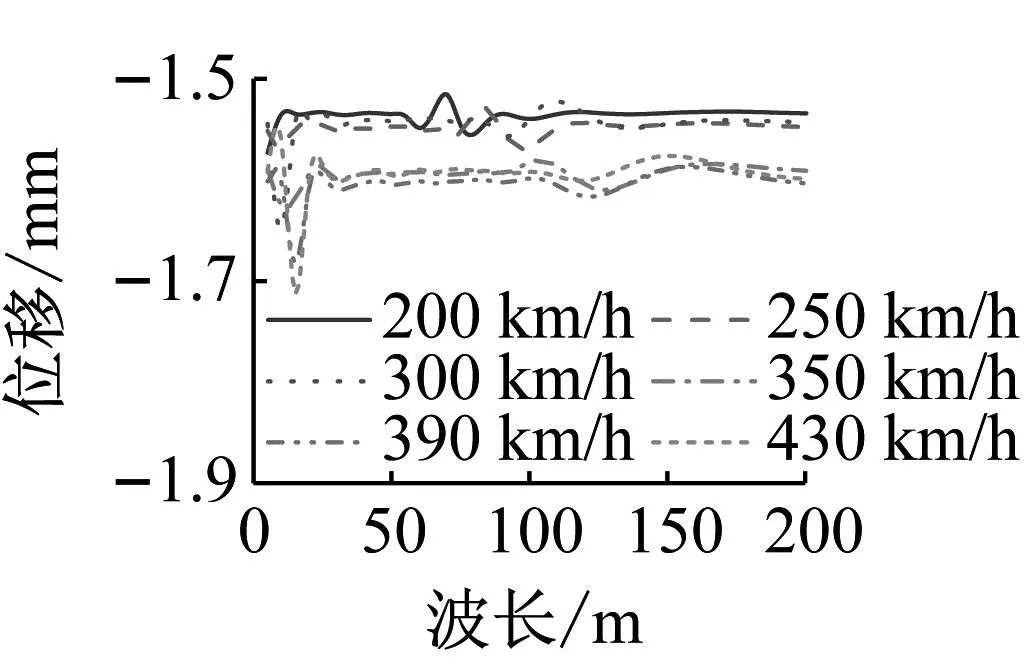
(a) 位移
4.3 列车运行平稳性分析
车辆运行平稳性是评价车辆走行性能的重要指标。由于目前没有制定磁浮列车走行性能的统一评价标准,本文参考铁道车辆动力性能评价规范。车辆运行平稳性主要与振动的幅值和大小有关,我国2019年发布了新国家标准GB/T 5599—2019《机车车辆动力学性能评定及试验鉴定规范》,采用Sperling平稳性指标对铁道车辆运行品质进行定量评估。Sperling 指标分为横向平稳性指标和竖向平稳性指标,当Sperling指标小于2.5时,平稳性等级为“优”,Sperling指标计算公式为
(9)
式中:A为振动加速度,m/s2;fv为振动频率,Hz;F(fv)为频率修正系数,具体取值见规范。
图22~图24给出了不同方向的轨道不平顺组合、不同轨道不平顺幅值和不同车速情况下车体的横向和竖向Sperling指标。由图22~图24可知,车体横向和竖向Sperling指标都小于2.5,平稳性等级为“优”,表明磁浮列车的运行平稳性良好。横向Sperling指标主要受横向不平顺的影响,竖向Sperling指标主要受竖向不平顺的影响。横向和竖向Sperling指标随轨道不平顺幅值增加而增加,与幅值基本呈线性关系。横向和竖向Sperling指标与车速没有明显关系。表7给出了不同工况下车体横竖向Sperling指标及平稳性等级。
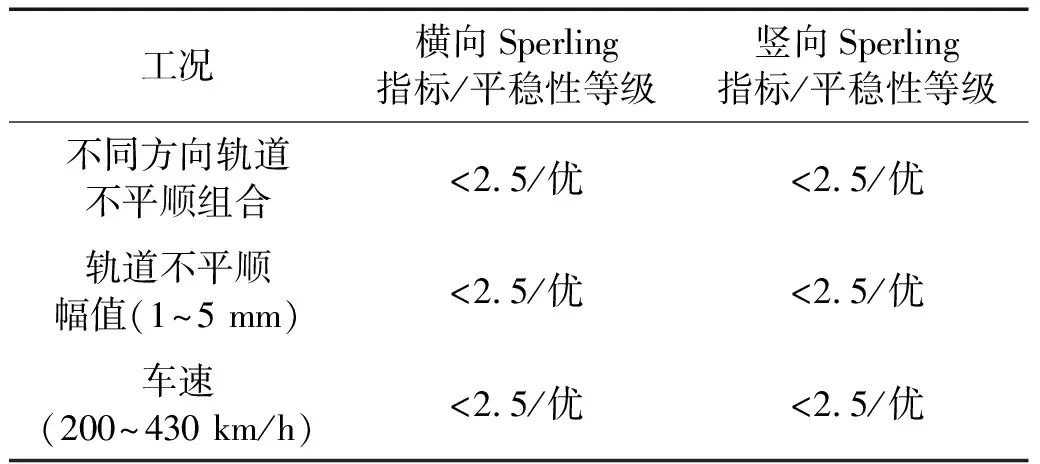
表7 不同工况下车体横竖向Sperling指标及平稳性等级
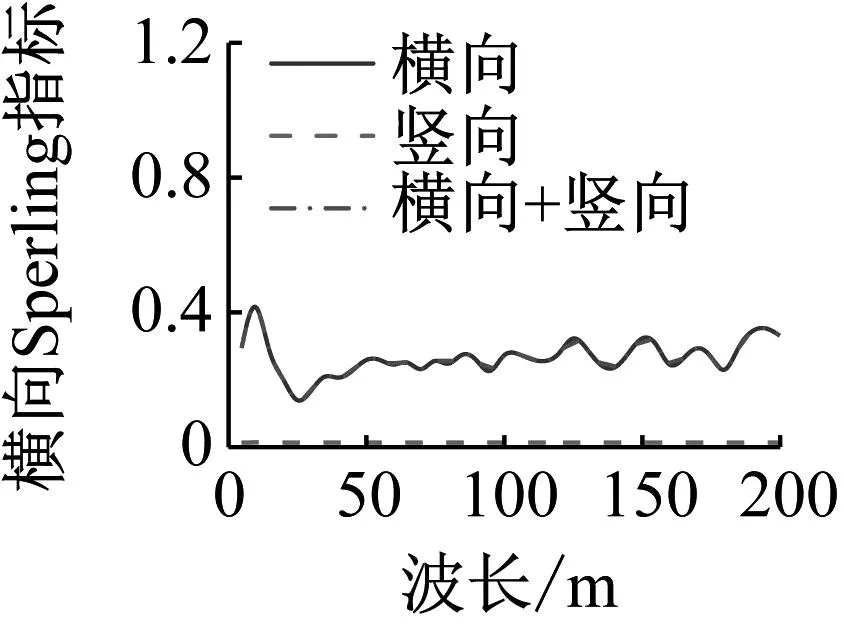
(a) 横向
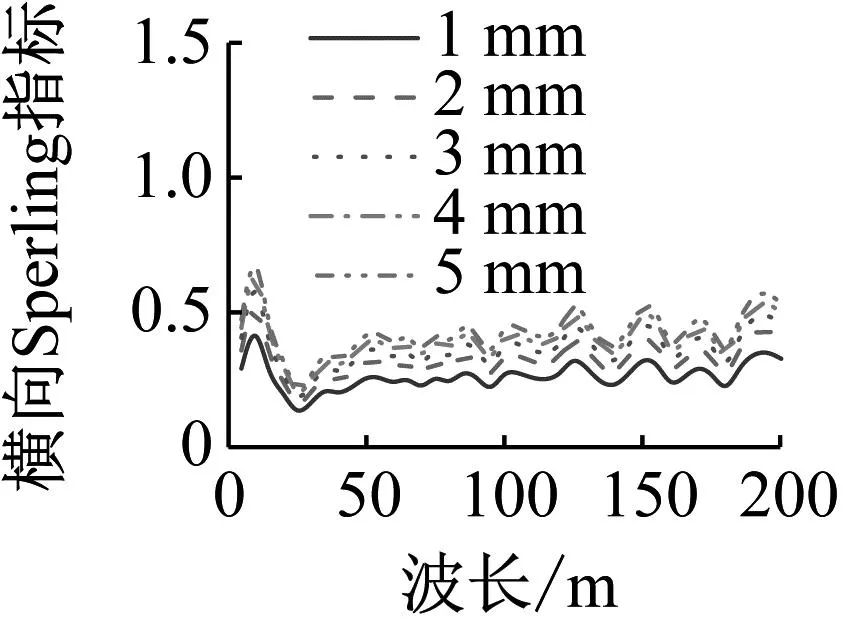
(a) 横向
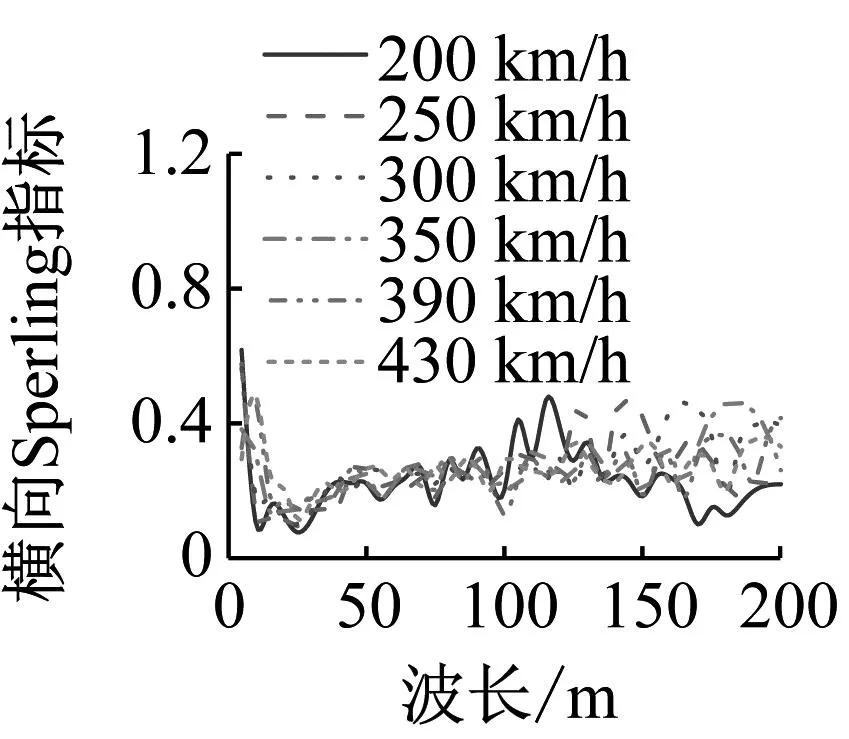
(a) 横向
5 结 论
本文通过建立高速磁浮列车-轨道梁耦合振动模型,施加正弦函数形式的轨道不平顺,分析了不同方向的轨道不平顺组合、不同轨道不平顺幅值和不同车速对车辆和桥梁动力响应敏感波长和列车运行平稳性的影响,得出以下结论:
(1) 车体横向、侧滚和摇头加速度主要受横向不平顺影响,竖向不平顺对其影响较小;车体竖向和点头向加速度主要受竖向不平顺影响,横向不平顺对其影响较小;磁浮列车-轨道梁系统的横向振动和竖向振动耦合性很弱。
(2) 在设计车速430 km/h下,波长为80 m、105 m、115 m、140 m和160 m时会分别引发车体侧滚、摇头、横向、点头和竖向方向的共振。
(3) 车体和主梁的动力响应幅值与轨道不平顺幅值基本呈线性关系。当轨道不平顺幅值为1 mm时,在计算车速200、250、300、350、390和430 km/h工况下,车体侧滚加速度幅值随车速变化不大,其他4个自由度方向的加速度幅值随着车速的增大而减小。主梁竖向加速度幅值随车速的增大呈线性增大。
(4) 从车体的横向和竖向Sperling指标可以看出,车体的Sperling指标均小于2.5,平稳性等级为“优”,磁浮列车的平稳性良好。

