TiAl 合金在高电位流动电解液中的庞加莱截面分析

刘伦峰，李 凌，王 鑫，李文元，廖翠姣

（湖南工业大学机械工程学院，湖南株洲 412007）

TiAl 合金因具有高比强度、抗高温、抗氧化、抗蠕变等性能， 已成为航空发动机低压涡轮叶盘的优选材料，在航空航天领域具有较大的应用前景[1-2]；然而，TiAl 合金的室温脆性、 低延展性及强化学亲和性导致采用传统机械加工表面完整性较差、 刀具磨损剧烈[3-4]。 电解加工因具有加工金属材料无残余应力、加工效率高、无刀具磨损等优点，逐渐成为加工TiAl 合金的优选方法[5-7]，但TiAl 合金本身具有不同电溶解行为的复杂微观组织与电解加工系统多因素耦合引起加工过程的非线性高维混沌特性，使TiAl 合金高稳定、高品质电解加工成为难题[8-9]。 因此，研究TiAl 合金在流动电解液中的溶解电化学系统的非线性动力学行为对探索TiAl 合金高品质稳定电解加工具有重要理论指导意义。

混沌系统有非线性、非周期性和不可预测性[10]，常用的研究方法有相空间重构吸引子轨迹[11]、Lyapunov 指数[12]、功率谱[13]等，但针对复杂高维混沌系统采用上述方法难以深入研究系统的具体形态特征，而庞加莱截面和差分庞加莱截面可通过降低系统维度研究系统结构特征以及其动态演化过程，是高维混沌系统的重要分析方法，在各领域得到广泛应用。 ARGOUL 等[14]采用庞加莱截面研究电解制锌的薄膜生长机理，发现该电解系统具有周期和非周期特征信号，系统的电压振荡经历了从周期加倍到混沌的动态演变过程。 CAO 等[15]采用庞加莱截面研究了分数阶阻尼摩擦冲击转子系统的非线性动力学行为，利用转子轨迹图、分岔图和庞加莱截面图反映了转速比、阻尼导数阶数和质量偏心度对系统非线性动力学行为的影响，发现周期加倍分岔、突然转变和从周期运动到混沌的三种混沌演变路径。MUKOUYAMA 等[16]通过庞加莱截面分析铂电极上H2O2和S2O82-的还原过程， 发现正反馈机制和两种不同时间尺度的负反馈机制的结合可以分别引起混沌振荡和混合振荡。 目前，庞加莱截面研究主要以定性分析为主，但一些高维复杂非线性系统仅定性分析无法达到深入研究目的，已有学者通过差分庞加莱截面结合其他量化手段来定量分析系统的特征规律。 霍铖宇[17]通过差分庞加莱截面的多尺度象限分布熵，定量描述了截面散点在不同区域和时间尺度上的分布状态特征，采用该法可分析不同生理病理状态下的心脏系统调控节律以及健康与典型病例状态下的心律差异。 目前，少见将庞加莱截面、差分庞加莱截面以及分布熵用于研究金属材料高电位溶解电化学系统非线性动力学特征的报道。

本文针对TiAl 合金电解加工系统的高维混沌特性，采用庞加莱截面、差分庞加莱截面及分布熵研究TiAl 合金在流动电解液中高电位电流密度时间序列的非线性动力学特征，揭示电解液压力对TiAl合金高电位溶解行为中非线性动力学稳定行为的影响规律。

1 实验方法与数据分析

1.1 实验方法

采用电化学工作站和数控电解加工机床进行实验，紫铜和5 mm×5 mm×10 mm 的Ti48Al2Cr2Nb 合金分别作为对电极和工件阳极。 采用恒电位法测试TiAl 合金高电位溶解行为，施加电压为16 V，工件电极进给速度为1.6 mm/min，测试时间为60 s，采样频率为10 000 Hz，采样数据量为600 000，电解液压力为0.2～0.5 MPa。对每个工件电极截面用游标卡尺测量3 次面积，用于电流修正得电流密度j。 为提高数据的可靠性，相同条件的实验至少重复三次。

1.2 去噪与相空间重构

本文采用去趋势变分模态分解法（VMD-DFA）对电流密度时间序列去噪[18-19]，具体思路是用变分模态法将原始时间序列分解为若干子序列， 求各个子序列对应的去噪因子αi， 当αi大于等于0.3 时保留该序列[20]，将保留的序列叠加得到去噪信号。该降噪方法具有较小的端点效应和良好的去噪鲁棒性，能够提升强非线性和高复杂时间序列的平稳性。

去噪后电流密度时间序列进行相空间重构[21]，电流密度时间序列为{j（t），t=1，2，3，…，n}，重构得到的空间序列为：

式中：Ji为第i个相点，i=1，2，3…，N；τ 为延迟时间参数；m为嵌入维数；N为相点数，N=n-（m-1）τ。

分别采用互信息法[22]和假近邻算法[23]确定式中的τ 和m， 从相空间重构的三维空间选择合适的平面绘制庞加莱截面， 截面的散点图反映电流密度时间序列在相空间的线性或非线性变化趋势以及分布态势[24]。

1.3 庞加莱截面及量化表征

庞加莱截面即庞加莱散点图， 通过降低非线性系统的维度简化系统， 揭示了非线性系统的演变规律[27]。当系统的庞加莱截面仅存在一个孤立点时，表示该系统呈现周期特征；当截面上分布N个孤立点时，表示该系统呈现周期N特征；当截面呈现一个闭合曲线，则说明该系统具有拟周期特征；当截面呈现出分散堆积的大量散点或者复杂的云状图形时，说明该系统为混沌系统[28]。

目前绘制庞加莱截面的常用方法是调整系统方程，通过计算方程的轨线和线面交点，将交点绘制成庞加莱截面。 电化学溶解实验采集到的电流密度时间序列是一维数据， 故本文提出针对电流密度时间序列的空间向量法并绘制其庞加莱截面。 通过定义一个合适的平面， 使相空间重构吸引子的轨迹线最大程度穿过该平面， 计算其顺时针或者逆时针穿过平面的交点， 由于TiAl 合金电解加工数据庞大，其重构后的数据点在空间中紧密相关且有序排列，所以空间两点之间的连接可用直线代替曲线拟合，即只需要记算出空间相邻两点所形成的直线与平面的所有交点。

对图1 的几何模型分析， 假设P1（x1，y1，z1）、P2（x2，y2，z2）为溶解电流密度时间序列中的两相邻点，给定平面α 为ax+by+cz+d=0 （平面方程为x=y），n==（a，b，c）为该平面的法向量，连接P1、P2所形成的直线与平面α 的交点设为点P，点P和点P2在法向量上的投影分别设为点D和点D2，可得下式：

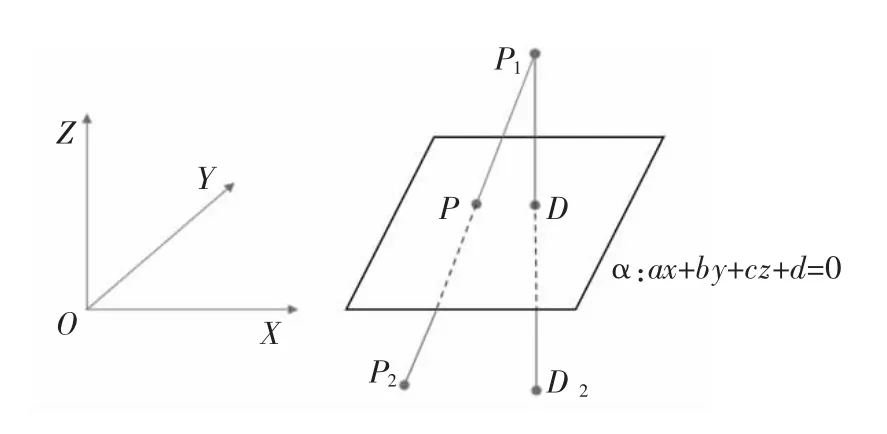
图1 直线与平面空间几何模型

其中，P1到平面的距离为：

P2到平面的距离即其在法向量上的投影为：

P1到D2距离为：

通过计算可得式（1）中n和向量OP：

通过向量OP的坐标P（x，y，z）类推，计算所有相邻两点形成的直线与平面的交点，得到一个与原始数据排列顺序一致的交点集。 当交点在原始数据相邻两点之间，且平面穿过两点形成的线段，则记录此点，最后将记录的交点绘制成散点图，即为所求的庞加莱截面。

为证明本文所提方法的正确性，用频闪法和本文方法分别绘制出经典杜芬方程（式8）的庞加莱截面（图2），默认ω=1、γ=1，调整参数δ=1.15，系统做拟周期运动。 由图中可看出，两种方法绘制的截面图完全相同，证明了本文所提出的空间向量法的可行性。

图2 杜芬方程庞加莱截面

1.4 差分庞加莱截面及量化表征

传统庞加莱截面能够定性分析电流密度时间序列的演变形态， 但无法更直观地反映电流密度的局部波动程度。 差分庞加莱截面通过去除时间序列的整体变化趋势而突出局部变化率[27]，即通过去趋势化作用直观表达出时间序列的局部波动程度。 设电流密度时间序列为j（t），其一阶差分序列为△j（t），以（△ji，△ji+1）为坐标绘制差分庞加莱截面。

本文采用分布熵量化表征差分庞加莱截面，可以分析不同象限、 不同半径区域内的差分庞加莱截面散点的分布聚集程度， 其值越大说明散点分布越均匀，反之说明散点趋近于集中在某些子区域[17]。分布熵计算以原点为中心作N个同心圆，rmax为最大同心圆的半径，第k个圆的半径为rk：

计算任意环形子区域或不同象限的扇形子区域的散点占总区域散点数的比例pi， 根据信息熵的定义计算差分庞加莱散点图的分布熵ED：

2 结果与分析

2.1 电流密度曲线

图3 是在不同电解液压力下TiAl 合金的电流密度时间序列曲线。在溶解初期，各条件电流密度的整体波动比较大，随着时间延长波动逐渐平稳，最终电流密度依次为0.4、0.2、0.5、0.3 MPa。 随着电解液压力增加， 电流密度曲线的局部波动逐渐变小，在0.4 MPa 和0.5 MPa 下局部波动基本相同。从电流密度曲线的整体与局部波动可知，TiAl 合金溶解经历了非均匀溶解逐渐转变到均匀溶解的过程， 随着电解压力增加溶解越来越平稳。

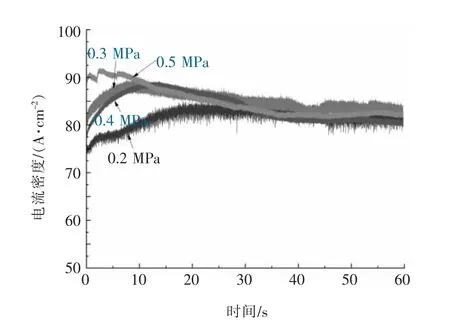
图3 不同电解液压力TiAl 合金的电流密度时间序列

2.2 相空间重构分析

图4 是选取电解液压力为0.4 MPa，在40～41 s时间范围的原始时间序列与用VMD-DFA 方法去噪后的时间序列。 对比去噪前、后信号可知，去噪信号基本保留了原始信号的波动形态，仅删除了大量随机信号，证明了本文去噪方法的可行性。

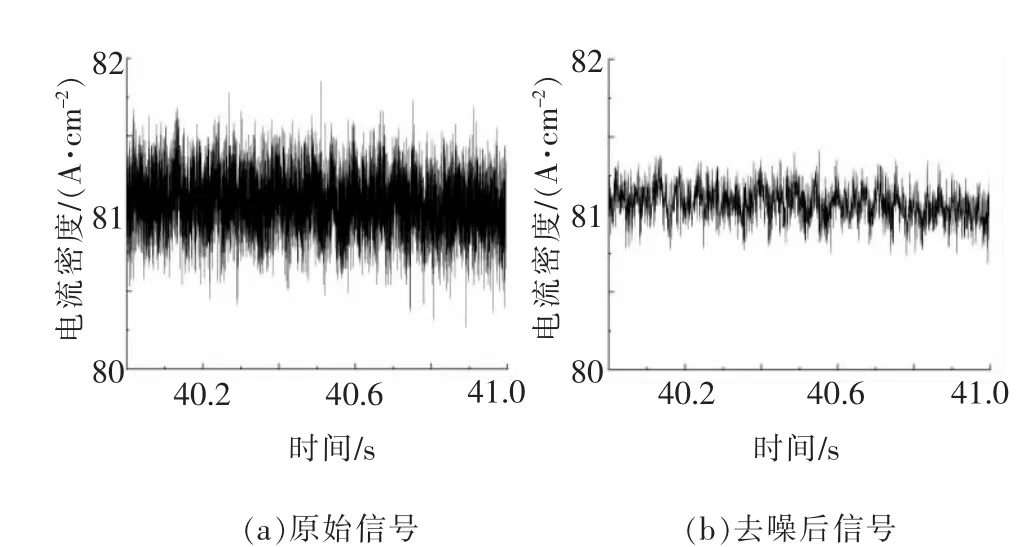
图4 0.4 MPa 在40～41 s 区间的原始信号与去噪信号

以{j（t），t=1，2，3，…，n}表示电流密度时间序列，重构序列则为Ji={j（i），j（i+τ），j（i+2τ），…，j[i+（m-2）τ]，j[i+（m-1）τ]}，通过计算时延和嵌入维数计算0.2～0.5 MPa 时延τ=10/5/5/5， 嵌入维数m=10/8/8/7。 以{j[i+（m-2）τ]，j[i+（m-1）τ]}为坐标绘制二维相空间重构图，不同电解液压力下的相空间重构图如图5 所示，箭头表示轨迹线运动方向。 由图可见，四种条件下的吸引子轨迹均对称分布在45°对角线上且具有复杂的拉伸、折叠和伸缩结构，在对角线方向的长度和具体结构均受电解压力的影响。 当电解压力为0.2 MPa 时，吸引子轨迹呈棒球状，且随着溶解时间延长垂直对角线方向的宽度逐渐变大；当电解压力为0.3 MPa 时，吸引子轨迹呈粗杆状，垂直对角线的方向变粗而对角线方向的长度在四个电解压力下最短；当电解压力为0.4 MPa 时，吸引子轨迹呈细杆状，对角线方向的长度变长而垂直对角线的方向变细；当电解压力为0.5 MPa 时，吸引子轨迹在对角线方向的长度继续变长而垂直对角线的方向未见明显变化，但有少数竹节结构。

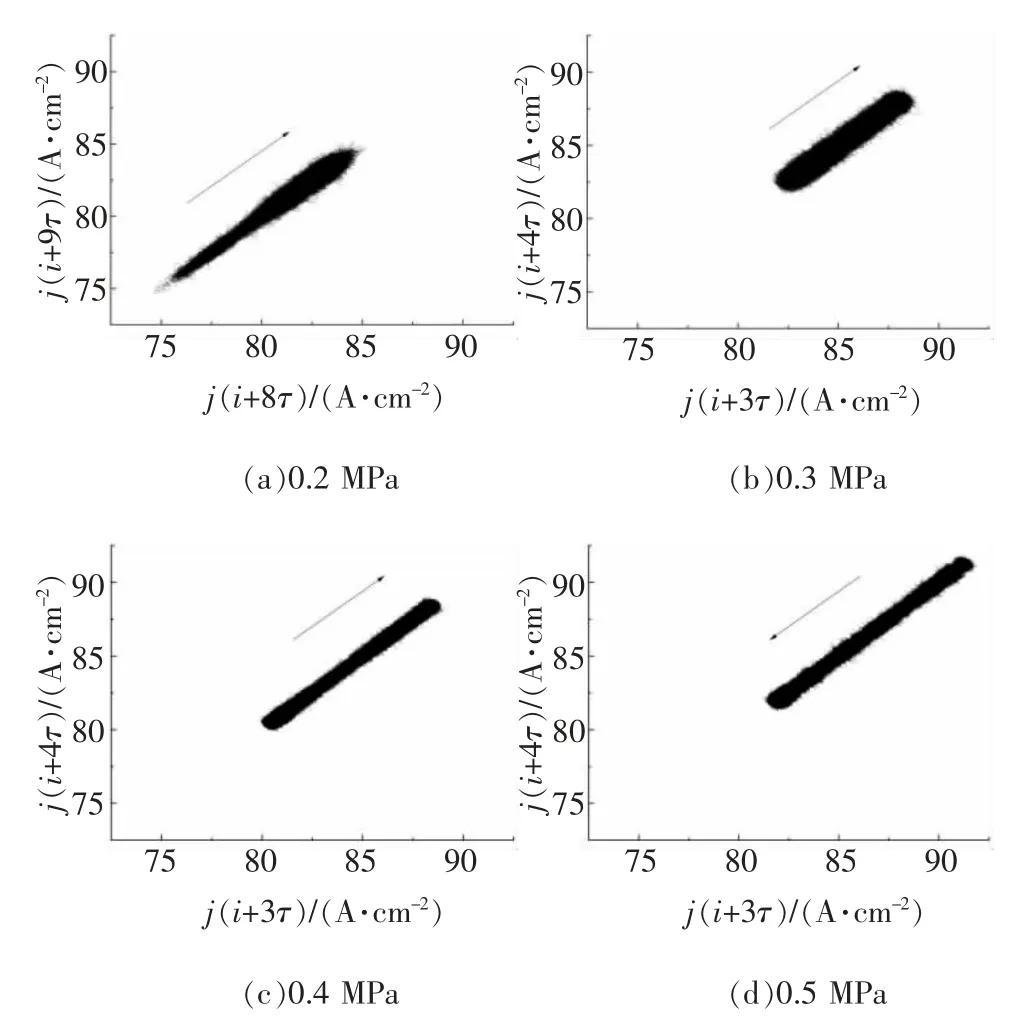
图5 不同电解液压力下相空间重构图

2.3 庞加莱截面分析

2.3.1 局部典型特征分析

此处用空间平面x=y切割三个具有典型特征的10 s 电流密度时间序列的三维相空间重构图， 包括上升小局部波动阶段、上升大局部波动阶段、平稳小局部波动阶段， 分别绘制庞加莱截面和差分庞加莱截面[28]如图6 所示。以截面坐标轴过原点的45°对角线为参照， 平行对角线的散点分布范围定义为庞加莱截面的长度， 垂直对角线的散点分布范围定义为庞加莱截面的宽度。 如图6a、图6d 所示，上升小局部波动和上升大局部波动的电流密度整体波动基本相同，但图6d 的电流密度局部波动更大，其对应的庞加莱截面（图6e）的散点分布更分散，对应的差分庞加莱截面的散点（图6f）主要分布在第二和第四象限；如图6a、图6g 所示，上升小局部波动和平稳小局部波动的电流密度局部波动程度相似，但图6a的电流密度整体变化程度更大， 其对应的庞加莱截面更长（图6b），两者的差分庞加莱截面散点（图6c和图6i）均主要分布在第二象限。

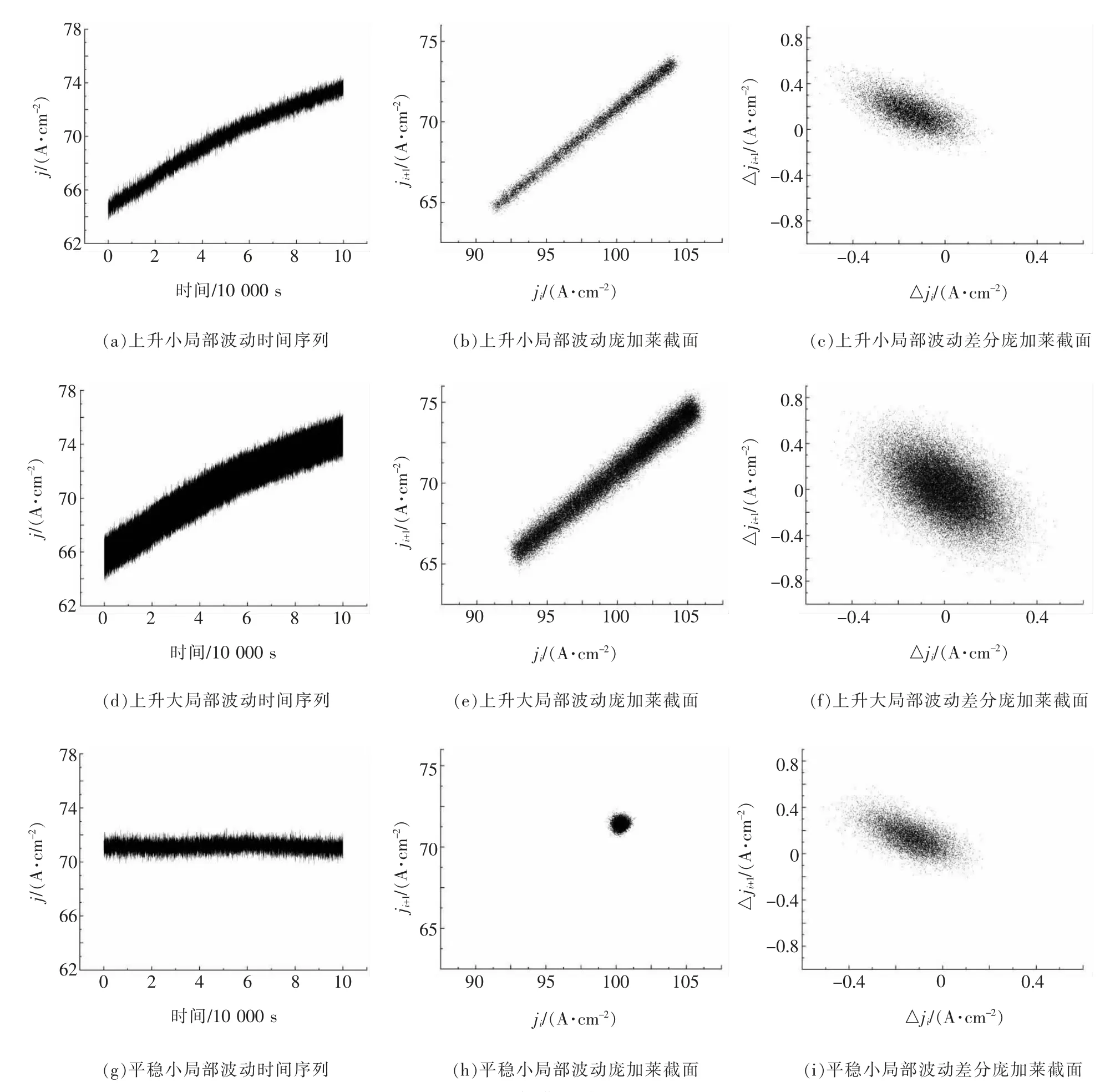
图6 局部典型特征分析图

总结可知，当电流密度整体波动较大时，庞加莱截面长度较长， 合金从非均匀溶解过渡到均匀溶解过程较长；当电流密度整体和局部波动均较小，庞加莱截面短且窄， 合金快速进入均匀且稳定的溶解过程，系统较平稳；当连续时间内相邻电流密度差值较大时，即局部波动大，庞加莱截面宽度较宽，合金局部溶解剧烈，系统平稳性较差。 而差分庞加莱截面主要反映了电流密度局部波动大小，散点分布集中且趋近于第二象限时，表明电流密度局部波动小，合金均匀溶解，系统更稳定。

2.3.2 整体特征分析

由不同阶段电流密度时间序列的庞加莱截面和差分庞加莱截面的特征和规律延伸至对全时段电流密度时间序列分析，如图7 所示。 由图可见，不同电解液压力下电流密度时间序列的庞加莱截面均呈现大量分散堆积的散点，证明了TiAl 合金流动溶解系统是一个典型的非线性非平稳的混沌系统[29]，且庞加莱截面的散点分布和相空间重构图的吸引子轨迹形状相似，但截面散点能够更清晰地反映出系统的形态特征和部分演变规律[30]。当电解压力为0.2 MPa时，庞加莱截面散点分布经历了从稀疏到集中过程，说明合金在溶解初期局部波动较小， 随着溶解时间延长局部波动变大后又逐渐变小再变大， 也说明该条件的电化学系统经历了发散到逐渐收敛的过程，也反映出合金在溶解过程中经历了由非均匀溶解缓慢过渡到均匀溶解的过程； 当电解压力为0.3 MPa时，庞加莱截面的长度变小而宽度变大，说明电流密度的整体波动变小、局部波动变大，合金快速进入均匀但不稳定的溶解过程；当电解压力为0.4 MPa 时，庞加莱截面的长度变大而宽度变小， 说明电流密度的整体波动又变大而局部波动变小， 合金快速进入均匀且稳定的溶解过程；当电解压力为0.5 MPa 时，庞加莱截面的长度继续变大而宽度未见明显变化，但有少数明显的散点凹陷现象，说明电流密度的整体波动进一步变大而局部波动基本不变，合金快速进入整体均匀而少数局部不稳定的溶解过程。

图7 不同电解液压力下的庞加莱截面

由于庞加莱截面宽度变化幅度并不明显，故采用差分庞加莱截面判断不同电解液压力下的电流密度变化速率。 图8 是在不同电解液压力下的差分庞加莱截面，在截面中的散点均主要分布在第二象限，随着电解液压力变大， 截面在0.3 MPa 时散点分布最均匀且分布区域最大， 在0.4 MPa 时散点分布最集中且分布区域最小。

图8 不同电解液压力下的差分庞加莱截面

表1 是通过计算截面整体及第二象限散点的分布熵对系统做定量分析， 可见电解压力为0.3 MPa时，全局和第二象限的散点分布熵均最大，说明此时差分庞加莱截面的散点分布最为均匀， 即电流密度变化速度最快、局部波动最大，系统稳定性差；而电解压力为0.4 MPa 时， 全局和第二象限的散点分布熵均最小，散点分布最集中，即电流密度变化速度最慢，合金溶解程度更为平缓，系统稳定性更好。 对不同压强下电流密度时间序列的定性和定量分析表明，虽然在0.3 MPa 电解压力下，电流密度整体变化程度不大， 但其较大的分布熵表示在局部溶解上反应过于剧烈，而在0.4 MPa 电解压力下，样品的整体变化程度和电流密度幅值波动起伏较小， 合金整体和局部的溶解平缓且均匀， 表明0.4 MPa 的电解压力更适合流动溶解实验，此时实验系统相对稳定。

表1 不同电解液压力下差分庞加莱截面的分布熵

3 结论

本文提出了空间向量法绘制庞加莱截面， 结合差分庞加莱截面和分布熵分析电解液压力对Ti-48Al-2Cr-2Nb 合金高电位电化学溶解系统的稳定性及影响规律，得出以下结论：

（1）TiAl 合金高电位溶解的电流密度时间序列的庞加莱散点分布在45°对角线上， 其长度和宽度分别与电流密度的整体波动和局部波动密切相关。

（2） 电流密度时间序列的庞加莱截面能够一定程度反映出合金溶解过程的动力学行为规律， 截面的形状大小随着电解液压力的增加而发生改变，截面的长宽与电流密度整体和局部波动变化成正比。

（3） 电流密度时间序列的差分庞加莱截面能够更直观反映合金局部溶解的剧烈程度， 该截面的分布熵与电流密度局部变化成反比。