带筋壁板筋条双侧激光喷丸成形研究
李宝旺,唐鑫森,王印博,江剑成,胡永祥
(1. 中车唐山机车车辆有限公司,河北唐山 064000;2. 上海交通大学机械与动力工程学院,机械系统与振动国家重点实验室,上海 200240)
为实现航空航天装备的轻量化, 同时满足装备的结构效率与性能, 带筋壁板越来越多地使用在航空航天装备设计中,例如机翼、机身、舱门等。 整体带筋壁板在外形上表现为筋条纵横分布, 具备结构效率高、气动外形优良等优点,是实现航空航天装备结构减重和整体性能提升的关键核心构件。 然而,复杂的筋条对整体壁板的弯曲存在强抑制作用,使得带筋壁板制造成本高、加工周期长、精度难保证,如何精准成形带筋壁板一直是成形制造中的难点问题[1]。 带筋壁板弯曲成形工艺主要包括滚弯成形、蠕变时效成形和喷丸成形,其中,滚弯成形易造成薄壁与筋条连接区域变形严重不均, 同时存在严重的变形回弹使得成形形状难以精确控制[2];蠕变时效成形需要专用大型热压罐,模具制造时间长、成本高、柔性差,并且只适用于具有时效硬化特性材料[3];机械喷丸通过喷射机械弹丸在薄壁结构表面引入塑性层,使带筋壁板产生整体弯曲变形,但弹丸撞击产生的塑性变形层深度一般小于200 μm,有限的塑性层深度使得其在面对高筋壁板时成形能力不足[4]。 目前,带筋整体壁板仍缺少有效的制造手段。
激光喷丸成形的原理是利用激光器发出高功率密度、短脉冲激光束冲击工件表面,覆盖在工件表面的吸收层数纳秒时间内吸收大量能量,吸收层蒸发并产生等离子体爆炸波。 由于约束层对等离子体的约束作用,等离子体爆炸产生的冲击波主要作用于工件表面,在工件表层引入梯度分布的塑性应变,造成工件的弯曲变形[5]。 相较于传统机械喷丸,激光喷丸的成形能力更强,引入的塑性层更深,还具备定位精确可控、工艺灵活等优点,能有效克服机械喷丸因弹丸落点随机而难以保证形状精度的缺点,是实现带筋整体壁板成形的有效途径[6]。 由于激光喷丸无模柔性成形的特点,传统方法难以保证成形精度,需要建立高效准确的数值模拟方法,实现带筋整体壁板高效的变形预测,为工艺参数设计提供途径。 固有应变方法[7]与固有矩方法[8],可用于模拟不包含筋条、凸台等结构特征的平板激光喷丸成形,受到领域内学者的广泛认可。 惠丁丁等[9]提出基于动态诱导应力进行激光喷丸成形模拟,但由于诱导应力对几何形状敏感,基于诱导应力的数值模型适用范围有限。针对带筋壁板,杨荣雪等[10]以固有应变方法为基础,实现带筋壁板的激光喷丸成形建模,但仅能模拟蒙皮喷丸下的带筋壁板变形,无法体现筋条双侧喷丸的效果。 考虑筋条双侧喷丸可拓展工艺参数作用范围,充分发挥激光喷丸的高柔性优势,提升工艺的形状调控能力,因此,有效模拟出筋条双侧喷丸的变形结果将为整体壁板的成形工艺设计提供支撑。
本研究考虑筋条双侧喷丸的带筋壁板激光喷丸成形的变形特征,并基于激光喷丸固有应变理论,推导了筋条双侧喷丸产生的等效弯矩解析计算公式,进而建立了筋条双侧喷丸的变形预测数值模型,并对模型的有效性进行了验证。
1 带筋壁板激光喷丸成形变形特性分析
首先基于实验分析带筋壁板在不同位置下激光喷丸的弯曲变形差异,掌握带筋壁板激光喷丸弯曲变形特征。 图1 是用于激光喷丸成形实验的带筋壁板试样的结构示意,试样材料为2024-T351 高强度铝板,采用的激光能量为8 J,光斑直径为4 mm,脉冲频率为5 Hz,光斑X、Y方向的搭接率为20%。
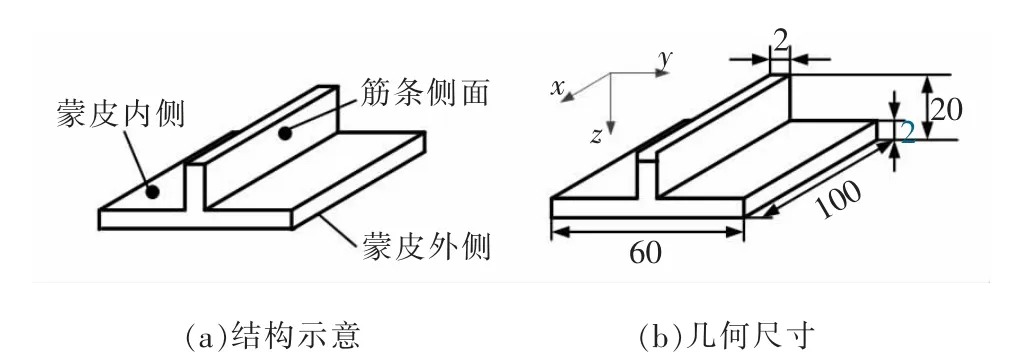
图1 带筋壁板结构示意图及试样几何尺寸
图2 是带筋壁板不同位置激光喷丸区域与喷丸路径, 蒙皮外侧和内侧的喷丸面积范围为86 mm×46 mm 和86 mm×40 mm。 对筋条侧面喷丸时,若采用单侧喷丸,会使带筋壁板产生侧弯,因此必须采用双侧喷丸,筋条双侧的喷丸面积为86 mm×8 mm。

图2 带筋壁板不同位置激光喷丸区域与喷丸路径示意图
图3 是带筋板试样在不同位置激光喷丸后的效果,使用三维形貌仪测量喷丸后试样的外形轮廓,对比带筋壁板不同位置激光喷丸弯曲变形差异, 结果如图4 所示,可见带筋壁板筋条双侧喷丸、蒙皮外侧喷丸、 蒙皮内侧喷丸后呈现出完全不同的弯曲变形特征。蒙皮外侧喷丸后,在X、Y两个方向上,带筋壁板均朝着远离激光入射方向弯曲,呈现凸曲面特征;蒙皮内侧喷丸后,在X方向上带筋壁板朝着靠近激光入射方向弯曲,而在Y方向朝着远离激光入射方向弯曲,呈现双曲特征;筋条双侧喷丸后,在X方向带筋壁板朝着Z轴正向弯曲;在Y方向带筋壁板朝着Z轴负向弯曲。 在X、Y方向上,带筋壁板筋条双侧喷丸与蒙皮内侧喷丸产生弯曲变形方向相反。X方向上, 带筋壁板筋条双侧喷丸弯曲变形显著大于蒙皮内侧喷丸弯曲变形,而Y方向弯曲变形较小。

图3 带筋壁板不同位置喷丸后试样

图4 带筋壁板喷丸后弯曲变形轮廓
图5 是带筋壁板筋条双侧激光喷丸弯曲变形机理。 激光喷丸产生的弯曲变形是厚度方向上不均匀分布残余压应力释放的结果,筋条单侧激光喷丸时,沿厚度方向不均匀分布的残余应力释放会使板件朝着远离激光入射的方向产生变形;双侧激光喷丸时,两次喷丸引入的不均匀分布残余压应力在厚度方向上对称,由残余压应力释放而产生的等效弯曲载荷相互抵消。 但是如图6 的变形示意,筋条双侧喷丸区域沿筋条长度方向会发生延展变形,由延展产生的弯矩使得带筋壁板产生的弯曲变形。 在X方向上,由于筋条延展,带筋壁板朝Z轴负向弯曲;在Y方向上,由于变形协调,带筋壁板朝Z轴正向弯曲。

图5 单侧喷丸与双侧喷丸激光喷丸变形行为
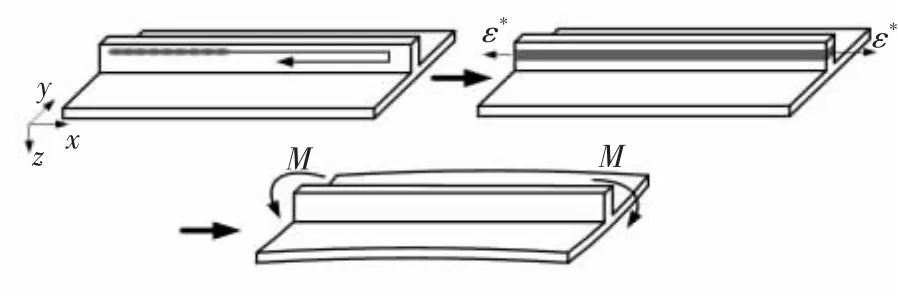
图6 带筋壁板筋条双侧喷丸弯曲变形示意图
综上所述, 带筋壁板筋条双侧激光喷丸与蒙皮激光喷丸产生的弯曲变形特征存在显著差异。 在激光喷丸成形工艺中, 考虑对带筋壁板筋条双侧区域进行喷丸,可拓宽工艺设计范围,有利于精确调控带筋壁板几何形状, 充分发挥激光喷丸成形的高柔性优势。
2 带筋壁板筋条双侧喷丸等效弯矩方法
2.1 等效弯矩理论推导
充分认识带筋壁板激光喷丸成形变形特性并掌握工艺规律, 进而建立带筋壁板的高效变形预测数值模型, 可为带筋壁板成形的工艺设计提供高效途径。本节提出一种筋条双侧喷丸的弯矩等效方法,建立带筋壁板筋条双侧激光喷丸模型, 从而实现带筋壁板筋条双侧激光喷丸成形的数值模拟。
固有应变是被领域内学者广泛认可的激光喷丸高效数值建模方法[11-12],平板单面激光喷丸形成的固有应变可被假定为高斯分布, 双侧激光喷丸作用下的固有应变分布与单侧喷丸存在差异, 需要重新推导分布。双侧喷丸条件下,其中一侧的固有应变与深度关系仍采用高斯函数描述,如下式所示:
式中:a1、b1、c1为高斯函数待定系数, 由激光喷丸工艺参数决定,可通过固有应变标定实验获得;z为深度。确定基准坐标系后,找出式(1)关于z=t/2 的对称函数, 即为另一侧面喷丸所产生的固有应变与深度关系函数,如下式所示:
式中:a2、b2、c2为高斯函数待定系数;t为板厚。 不考虑变形几何效应, 双侧激光喷丸所产生的固有应变分布可由两次单侧激光喷丸产生的固有应变叠加获得,即:
当双面激光喷丸所使用的激光喷丸参数一致时,有a1=b1、a2=b2、c1=c2。 单侧喷丸与双侧喷丸对应的固有应变关系如图7 所示, 可见两者之间有很大的差异。

图7 固有应变与深度关系
进一步,为确定带筋壁板在筋条长度方向上由激光喷丸产生的等效弯矩,首先计算带筋壁板的形心位置,通过形心位置反映带筋壁板的几何尺寸,如图8 所示。 图中,c为形心位置,zs、ze分别是激光喷丸开始位置与结束位置。

图8 带筋壁板形心轴及几何参数示意图
根据截面形心计算公式[13],可得带筋壁板形心坐标的表达如下式所示:
式中:B为壁板宽度;t为筋条宽度;h为壁板厚度;H为壁板总高度。 进而计算得到带筋壁板截面惯性矩如下式所示:
式中:z2为带筋壁板形心坐标余量, 可通过H与z1相减而得。
将X向和Z向的固有应变分别记为εx*、εz*,基于带筋壁板筋条双侧喷丸弯曲变形分析结果可知,εz*会使构件整体产生沿Z轴方向的微小位移,但几乎不会影响构件的弯曲变形, 因此在计算筋条双侧喷丸产生的等效弯矩时忽略εz*的影响,将带筋壁板筋条喷丸弯曲变形看作一维问题。 在基于连续介质假设的静力学分析范畴内, 由固有应变引起的应力问题可由弹性力学基本方程解决,可求得应力σx与固有应变εdx*之间的关系如下式所示:
式中:E为弹性模量。由于应力分布在带筋壁板截面上并非关于中性轴对称, 则可计算出由应力产生的弯矩, 此弯矩即为带筋壁板筋条双侧激光喷丸所产生的等效弯矩,如下式所示:
等效弯矩反映带筋壁板筋条双侧激光喷丸中的构件几何尺寸以及工艺参数, 可用来预测筋条双侧喷丸条件下的带筋壁板弯曲变形。
2.2 等效弯矩数值验证
固有应变模型是广受认可的喷丸成形数值模拟方法, 本节通过对比固有应变模型与等效弯矩模型的仿真结果, 验证等效弯矩模型的正确性。 在ABAQUS 软件中建立带筋壁板筋条喷丸固有应变模型, 将等效弯矩模型仿真结果与固有应变模型仿真结果进行对比,验证筋条喷丸等效弯矩的正确性。
基于ABAQUS 建立带筋壁板筋条双侧激光喷丸等效弯矩模型, 用以预测带筋壁板筋条双侧喷丸弯曲变形。建模首先是模型的网格划分,建立带筋壁板实体模型后对其进行网格划分, 选用单元类型为八节点减缩积分单元C3D8R; 其次是边界条件设置,为避免刚体位移,仅在带筋壁板蒙皮外侧中心处施加固定约束,如图9a 所示;最后是施加载荷,由于不能直接在实体单元上施加弯矩, 在带筋壁板截面施加等效弯矩前,需要在该截面上创建一个如图9b所示的参考点,将参考点与带筋壁板截面进行耦合,并将弯矩施加在参考点上。 根据激光喷丸工艺参数确定固有应变分布函数,将固有应变、带筋壁板几何尺寸及激光喷丸区域带入式(7),求得施加的等效弯矩, 最后通过一次弹性计算求得到带筋壁板筋条双侧喷丸弯曲变形。

图9 带筋壁板建模设置
验证模型几何尺寸与带筋壁板试样保持一致,弹性模量为68 GPa,泊松比为0.33。 对于等效弯矩模型,采用等效弯矩作为输入;对于固有应变模型,采用固有应变作为输入, 其余模型参数保持一致。单侧激光喷丸引入的固有应变如下式所示:
式中:ax=0.005 3、bx=0.238 2、cx=0.872 3、az=0.001 8、bz=0.238 2、cz=0.872 3,将式(8)带入式(3)中可以得到双侧激光喷丸固有应变,在固有应变模型中施加的固有应变如下式所示:
式中:t为筋条宽度。 将式(9)中(y)带入式(7)中可计算得筋条喷丸等效弯矩为40 425 N·mm。图10是基于固有应变模型的等效弯矩模型, 其中图10a为激光喷丸区域,图10b 为施加等效弯矩的筋条双侧喷丸模型, 图10c 为施加固有应变的筋条喷丸双侧喷丸模型。

图10 基于固有应变模型的等效弯矩模型验证
图11 是等效弯矩模型与固有应变模型仿真结果。 提取蒙皮外侧中线位置单元节点的位移绘制带筋壁板的弯曲变形轮廓,获得等效弯矩模型与固有应变模型的弯曲变形轮廓对比如图12 所示。 由图12 可见,等效弯矩模型与固有应变模型仿真所得带筋壁板弯曲变形轮廓变形趋势一致,最大误差出现在带筋壁板端面处。 在X方向上,等效弯矩模型仿真结果的弧高为0.223 8 mm,固有应变模型仿真结果的弧高为0.212 3 mm,两者相对误差小于5.5%。
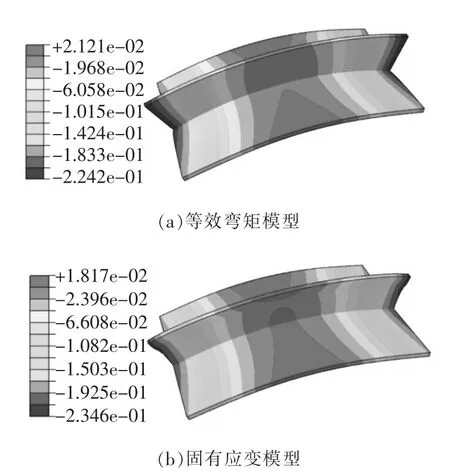
图11 带筋壁板筋条喷丸仿真结果
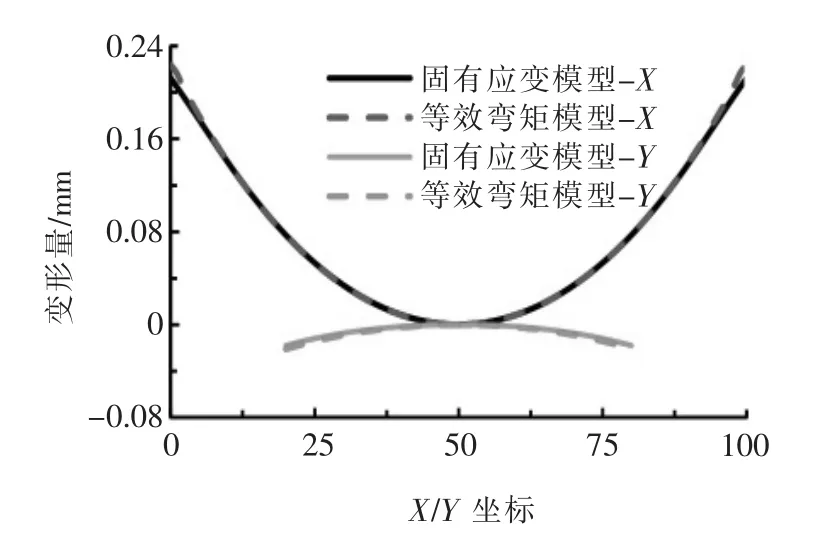
图12 等效弯矩模型与固有应变模型弯曲变形轮廓
在数值仿真划分网格时,单元尺寸对于仿真结果的准确性具有重要影响, 有必要分析网格尺寸对于等效弯矩模型收敛性的影响。图13 是建立不同网格尺寸的带筋壁板筋条双侧喷丸等效弯矩仿真模型,仿真模型单元尺寸分别为0.5、1、1.5、3 mm,可见不同网格尺寸带筋壁板仿真位移云图基本一致,节点位移量存在微小差别。

图13 不同网格尺寸带筋壁板筋条双侧喷丸仿真结果
为进一步比较不同网格尺寸下仿真结果的差异,提取各模型弧高,得到表1 的弧高对比,可见网格尺寸从0.5 mm 增加到3 mm,弧高变化小于1%,对于带筋壁板弯曲变形影响较小,因而等效弯矩模型具有良好的网格收敛性。
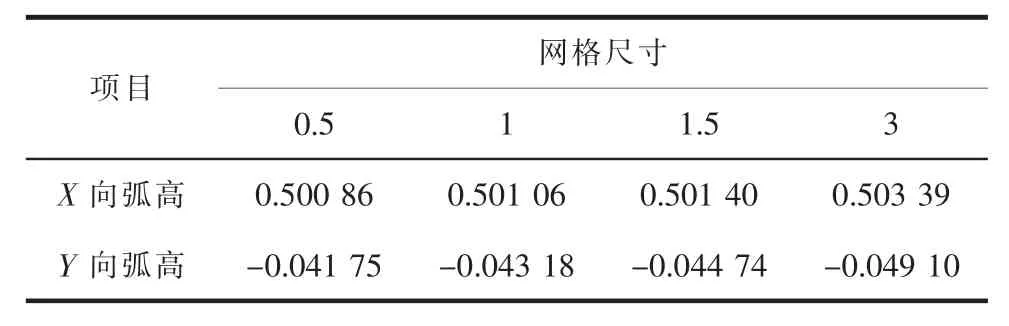
表1 不同网格尺寸带筋壁板仿真模型弧高单位:mm
3 结论
本研究针对带筋壁板激光喷丸成形,分析了带筋壁板的激光喷丸成形变形特性,并对不同区域进行喷丸所产生的变形结果进行论证。 考虑到目前缺少面向带筋壁板筋条双侧激光喷丸的变形预测数值模型,基于固有应变理论,推导得到筋条双侧喷丸所产生的等效弯矩解析计算公式,并建立了筋条双侧喷丸等效弯矩数值模型。 为验证所提出的数值建模方法的有效性,比较分析了实验与数值模拟下的变形结果,结果表明,建立的数值模型能有效预测带筋壁板筋条双侧激光喷丸的变形结果,有望带筋壁板激光喷丸成形的工艺预测与规划提供有效途径。

