双有源全桥变换器无模型预测控制策略
操建生,于新红,许立斌,汪凤翔
(1.福建农林大学 机电工程学院,福州 350100;2.中国科学院海西研究院泉州装备制造研究中心,泉州 362216)
0 引 言
双有源全桥(dual active bridge,DAB)变换器以良好的电气隔离、双向功率流、高功率密度、易于零电压开通等特点,近年来备受新能源汽车、储能等领域的青睐[1-3]。
DAB变换器传统控制方式主要采用比例积分(proportional integral,PI)控制。然而,在面对非线性外部干扰时,PI控制难以满足时变工况下系统的稳定性需求,同时PI存在积分饱和问题进而导致系统动态响应变慢[4-5]。模型预测控制(model predictive control,MPC)算法不仅具备良好的动态特性,且能适应系统的非线性和时变性,由于过度依赖模型参数,应用于DAB变换器时控制性能受到模型精度、温度和磁场干扰等影响[6-7]。文献[8]提出了DAB的MPC控制方法,虽有效提升了变换器的动态响应,但由于MPC算法的参数依赖性问题,参数失配时系统的鲁棒性和稳态性较差。
基于超局部的无模型预测控制不依赖系统物理参数,能够适用多样系统,近年来被国内外学者广泛研究[9-10]。文献[11]提出一种无模型预测功率控制,有效提高了系统的鲁棒性,相较于传统功率预测控制,该方法具有更高的功率稳态纹波,主要是超局部中动态部分估计存在较大误差。文献[12]提出DAB变换器的超局部控制,并采用滑模观测器对超局部中动态部分进行估计并补偿,提升了变换器稳定性及鲁棒性。然而,所设计的超局部控制器本质上仍采用了PI控制,难以满足非线性时变工况下变换器的控制需求。
为了进一步提升DAB变换器的控制性能,本文提出一种基于线性扩张状态观测器的无模型预测控制(model-free predictive control based on linear extended state observer,LESO-MFPC)策略,基于DAB系统控制输入、输出变量关系构建超局部模型,结合线性扩张状态观测器(linear extended state observer,LESO)良好的观测特性,对超局部模型中的动态部分进行估计以及补偿,并通过李雅普诺夫稳定性理论证明了LESO的稳定性。最后搭建实验平台,验证了本文所提LESO-MFPC策略的有效性和优越性。
1 双有源全桥变换器
DAB变换器主电路拓扑如图1所示。其中,S1~S4、S5~S8分别为变压器原、副边全桥功率开关器件;Uin和Uo分别为变换器原、副边直流端电压;Uh1和Uh2分别为变压器两侧全桥的输出交流方波电压;Cin为变换器的输入侧稳压电容;Co为输出侧滤波电容;Ld为原边电感;Rs为输出侧负载;iLd为原边电感电流;变压器变比为n∶1。
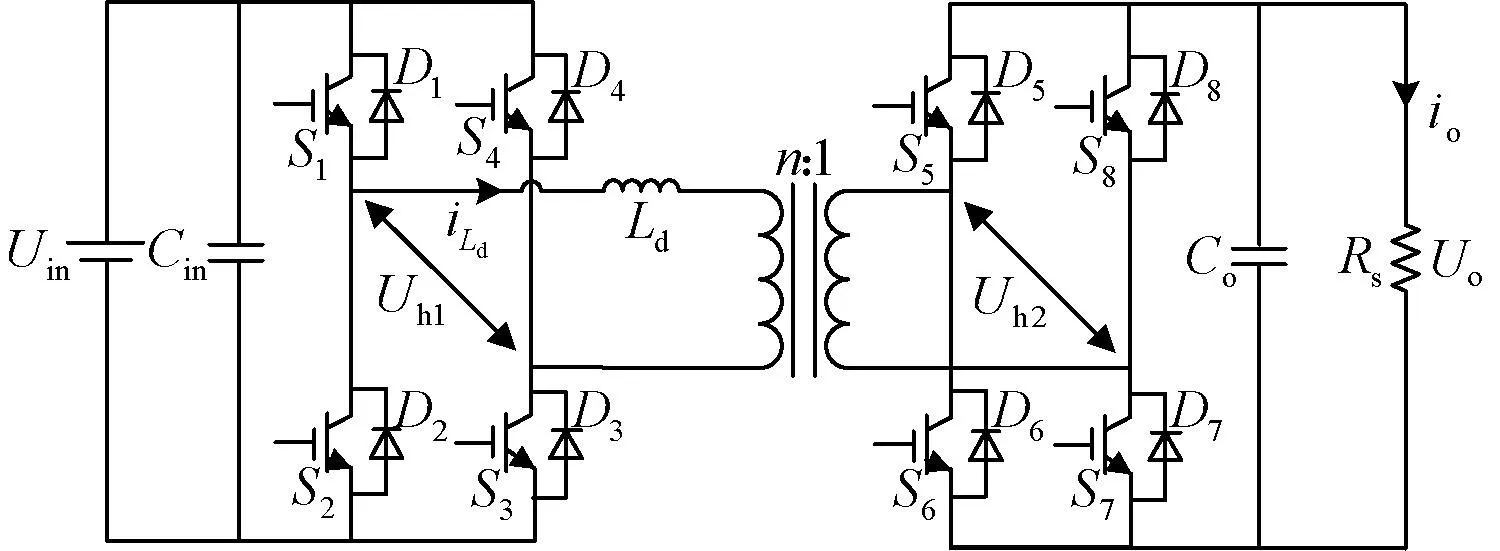
图1 双有源全桥DC/DC变换器拓扑结构
1.1 移相调制工作原理
采用经典的移相调制方法进行控制,其稳态时的工作波形如图2所示。定义每个全桥的上、下开关管互补导通180°,对角开关管均保持同相位,所有开关管均保持50%固定占空比,其中,D为开关管S1S3和S5S7控制信号之间产生的移相比;Ts为一个开关周期;Ths为半个开关周期。
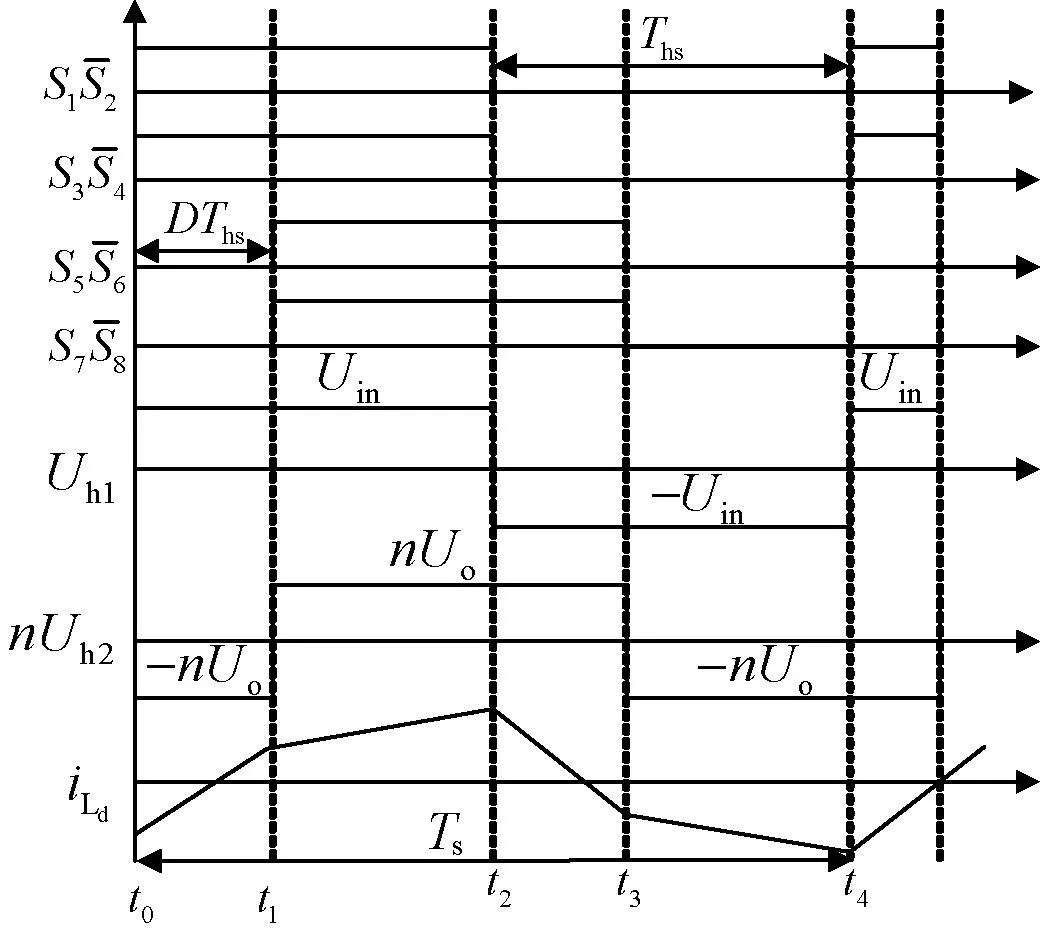
图2 移相调制下工作波形
1.2 变换器特性分析
由图2可知,DAB移相调制下的工作波形呈半波对称,因此一个周期内的传输功率可以表示:
(1)
根据电磁感应定律以及电感元件的韦安特性,可以得到移相调制下电感电流iLd各节点关系式:
(2)
根据伏秒平衡原理,电感电流波形在半个周期内呈正负对称,因此可得:
(3)
从而可以得到DAB变换器传递的有功功率:
(4)
2 DAB变换器模型预测控制
2.1 状态平均模型
由于DAB变换器的强非线性特性,其建模与控制颇具挑战,在此通过状态空间平均建模法,建立DAB的降阶大信号模型。DAB变换器的平均值等效电路如图3所示。其中,i2、io、iCo分别表示输出侧电流,负载电流及流过输出侧电容的电流。

图3 平均值等效电路
根据功率守恒定律,负载功率即为变换器输出功率,因此得到变压器副边全桥直流输出侧电流i2:
(5)
根据基尔霍夫电流定律以及电容元件电压电流关系,得到输出侧电压方程:
(6)
输出电压微分项在某种程度上反映了输出电压的变化趋势。对式(6)进行离散化,得到DAB变换器的预测模型:

(7)
式中:Uin(k),Uo(k)和D(k)为k时刻采样实际输入电压、输出电压和移相比;Uo(k+1)为k+1时刻输出电压预测值。
2.2 最优移相比计算与分析
为了实现DAB变换器直流侧输出电压的稳定性。根据式(1)输出电压的预测模型,构建如下成本函数:
(8)
由此得到,成本函数的旨在实现k+1时刻的预测电压值精准跟随参考电压值,g越小,跟随效果越好。因此,将式(7)带入成本函数中并求导,可得:
(9)
式中:ζ=Co/Ns为期望周期系数。
当输出电压实际值与参考值相差较大时,如果输出电压的实际值在一个控制周期跟踪上参考电压值,会导致输入功率急剧增大,系统的稳态性能变差。令电压的实际值在Ns个控制周期跟踪上参考值,通过对Ns的合理选取满足实际工程中不同的动态性能要求[13]。
式(9)中,Dm(k)=D(k)[1-D(k)]为移相比函数关系式。通过移相比的函数关系,可求得最优控制移相比:
(10)
由上述分析可知,MPC主要通过模型参数及当前时刻采样值进行预测,以获得下一时刻的最优控制移相比,进而实现预测值精准跟随参考值。DAB变换器降阶大信号模型精度较差,因此MPC算法下控制性能较差。超局部模型能够降低控制系统对模型的依赖性,且随着系统运行条件的变化其适应性更强,然而,传统超局部模型应用在实际工况中存在采样频率低、动态响应慢、对传感器精度要求较高等问题,引入观测器可以提高对超局部模型中动态部分的估计精度,实现更好的控制。
3 DAB变换器无模型预测控制
3.1 超局部模型
由DAB变换器平均值等效电路可知,其大信号降阶模型显然为一阶系统,因此结合式(6),得到系统的超局部模型:
(11)
对式(11)进行离散化处理,可以得到DAB变换器的离散超局部模型:
Uo(k+1)=Uo(k)+Ts[α(k)Dm(k)+flu(k)]
(12)
所构造成本函数与传统MPC方法相同,将式(12)代入式(8)并求导,计算得到k时刻所需的最优控制移相比函数关系式:
(13)
3.2 LESO设计
为了有效地估计DAB变换器超局部模型控制系统中的动态部分,设计LESO对系统集总扰动进行估计,并实时补偿到控制器中,式(11)中系统状态方程:
(14)
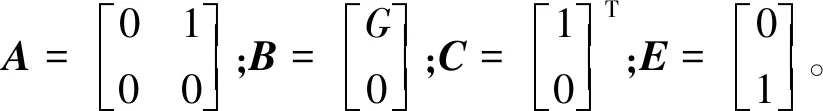
对式(14)进行状态重构,可设计二阶LESO:
(15)
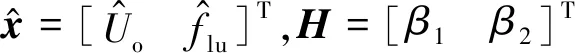
为了验证观测器的收敛性和稳定性,由计算可得观测器误差e所满足关系式如下:
(16)
根据李雅普诺夫稳定性判据,只需综合扰动有界,合理选取增益矩阵H的系数,使得Ae的特征值落于左半平面即可保证误差趋近于0。因此设计LESO的一对重合极点-ω0作为期望极点,则可进一步得到期望的特征方程:
λ1(s)=|sI-[A-HC]|=s2+γ1s+γ2=(s+ω0)2
(17)
式中:ω0是LESO的带宽。
特征方程的根都落在负半轴方可确保观测器稳定,因此增益系数设计:
(18)
通过整定ω0的大小,确定γ1、γ2的大小,简化整定过程,同时还需保证ω0>0,观测器即可保持稳定。
3.3 LESO-MFPC设计
为了有效地估计超局部模型中的增益和动态部分,设计LESO对系统集总扰动进行估计,并实时补偿到控制器中。式(12)中系统状态方程可以写为:
(19)
(20)
本文所提LESO-MFPC控制策略,具体控制结构框图设计如图4所示。
4 实验验证
为了验证LESO-MFPC算法的控制性能,本文以TMS320F28335为主控芯片,搭建DAB实验样机,实验平台如图5所示,开关频率为50 kHz。具体实验参数见表1。

表1 实验系统参数

图5 实验平台
选用基于传统PI补偿的MPC算法(PI-MPC)作为比较方法,并在多种实验工况下进行对比,以此体现LESO-MFPC算法的良好动态性、稳态性以及鲁棒性。
4.1 输出侧电压阶跃对比试验
为了验证LESO-MFPC算法动态性能,进行输出电压阶跃实验。输入电压为200 V,负载保持在5 Ω,两种算法的期望周期调整系数Ns均设置为30,实验结果如图6所示。
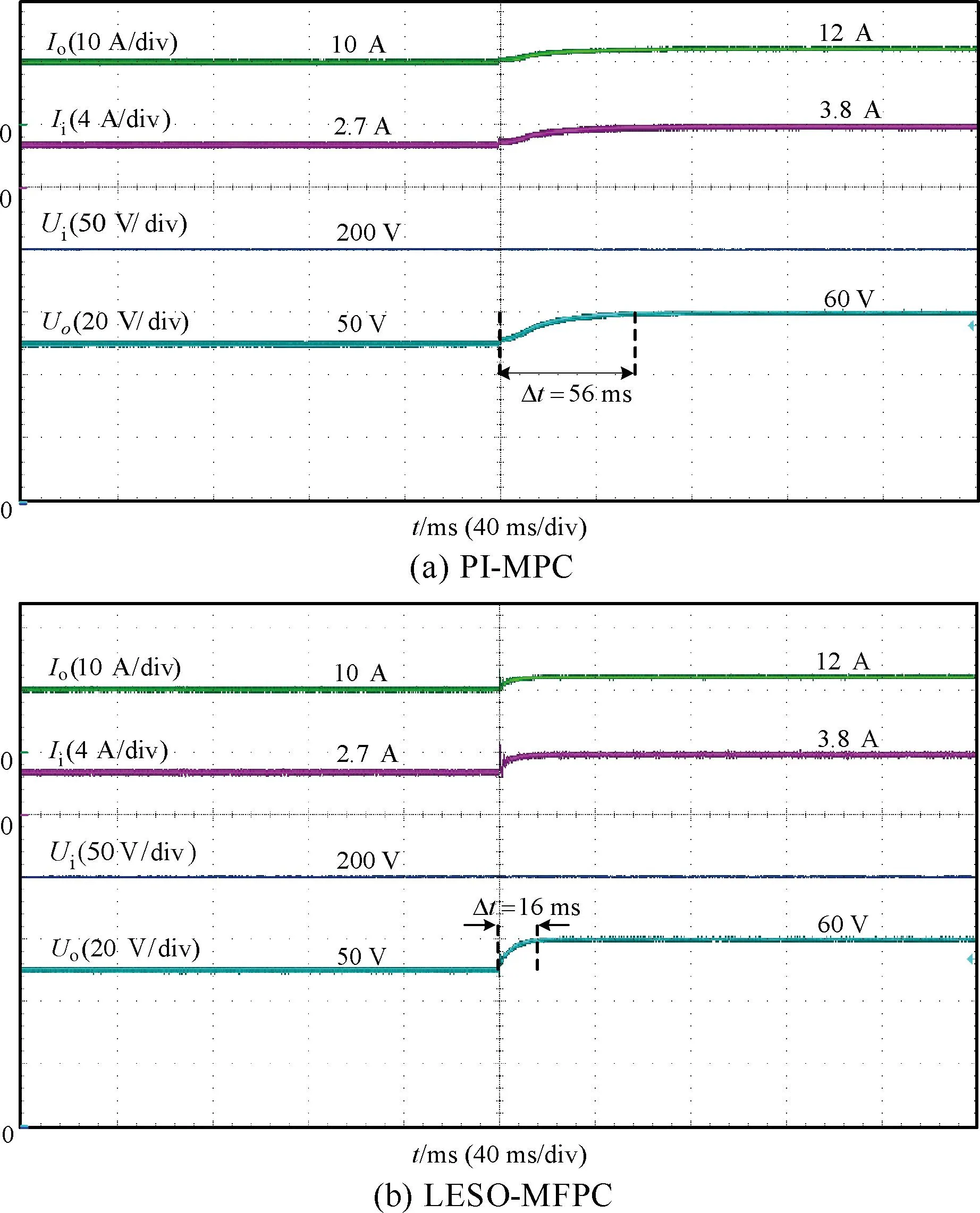
图6 电压阶跃变化实验结果
输出电压由50 V阶跃至60 V时,图6(a)中,PI-MPC算法输出电压恢复稳态所需时间约为56 ms;图6(b)中,LESO-MFPC算法输出电压恢复时间约为15 ms。实验结果表明,LESO-MFPC具有更快的动态响应速度。
4.2 负载突变对比实验
为了验证负载扰动下LESO-MFPC算法的控制性能,对变换器进行负载突变实验。输入电压为20 V,输出电压保持在50 V,实验结果如图7所示。当变换器的负载由10 Ω突减至5 Ω时,图7(a)所示,PI-MPC算法的输出电压降落了12 V,输出电压恢复至新稳态调节时间约为38 ms;图7(b)所示,LESO-MFPC算法的输出电压降落了2 V,输出电压恢复至新稳态调节时间约为5 ms。实验结果表明,LESO-MFPC算法具备更强的抗负载扰动能力。
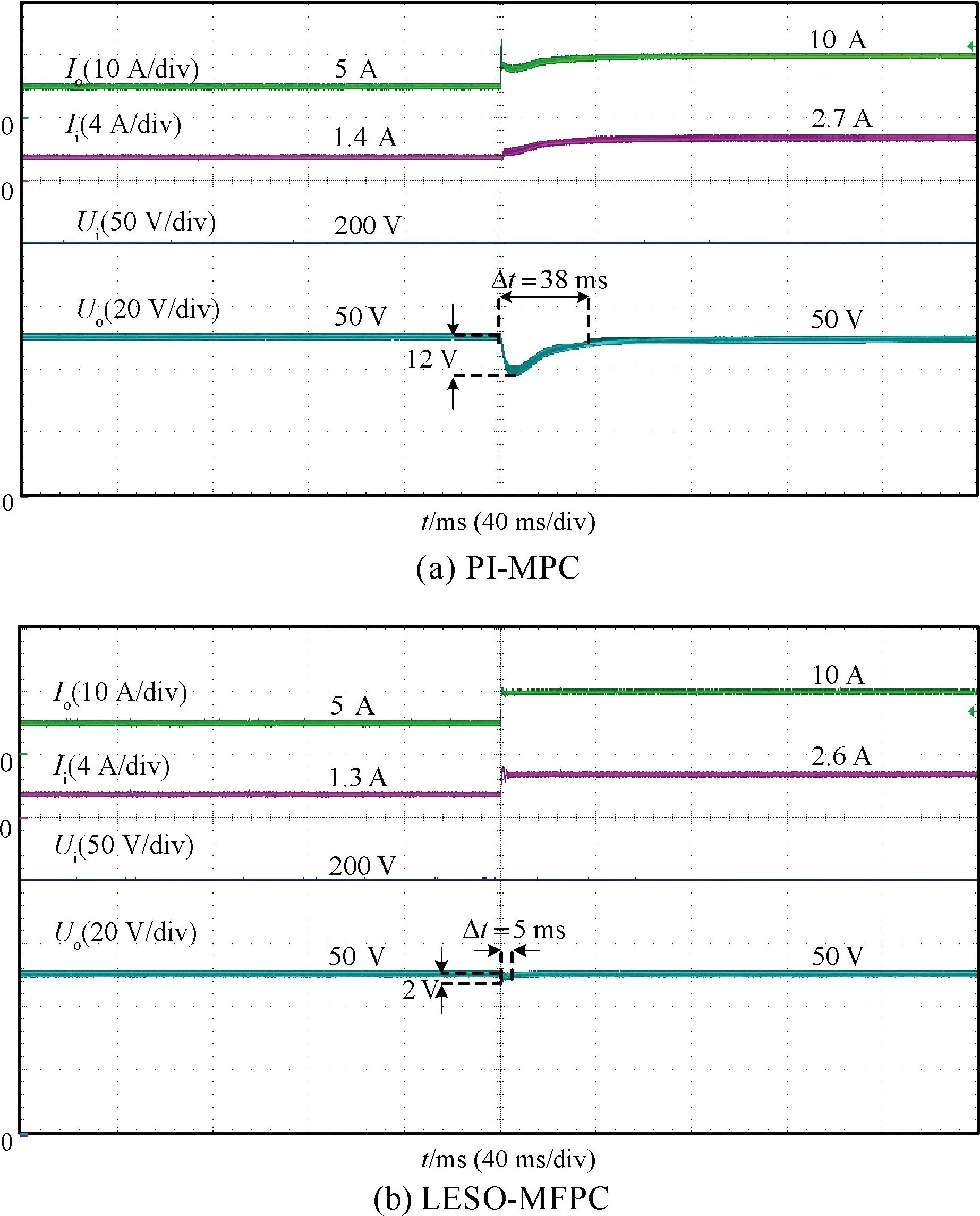
图7 负载突变实验结果
4.3 输入侧电压阶跃对比实验
为了进一步验证LESO-MFPC算法在输入电压波动时的动态特性,对变换器进行输入电压阶跃实验。输出电压为50V,负载保持在5 Ω,实验结果如图8所示。输入电压由150 V阶跃至200 V时,图8(a)所示,PI-MPC算法输出电压超调量为8.5 V,输出电压恢复至新稳态的调节时间为64 ms,输出电压超调量为8.5 V;图8(b)所示,LESO-MFPC算法输出电压几乎不发生波动,输出电压恢复至新稳态调节时间约为12 ms。实验结果表明,LESO-MFPC算法在输入电压阶跃时,具备更优的动态特性。

图8 输入侧电压阶跃实验结果
4.4 电感失配对比实验
为了验证LESO-MFPC算法对电感参数的敏感性,设置电感失配对比实验。电感参数从Ld突降至0.5Ld,实验结果如图9所示。PI-MPC算法输出电压降落了5V,调节时间约为11 ms,电感电流波动为1.8 A;LESO-MFPC算法输出电压降落了2 V,调节时间约为4 ms,电感电流几乎不发生波动。实验结果表明,电感突降时,LESO-MFPC算法鲁棒性更强,抗干扰能力更强。

图9 电感突减实验结果
电感参数从Ld倍突增至2Ld时,实验结果如图10所示。PI-MPC算法输出电压超调量为8 V,调节时间约为8 ms,电感电流波动为4 A;LESO-MFPC算法输出电压超调量为4 V,调节时间约为5 ms,电感电流波动为3 A。验结果表明,电感突增时,LESO-MFPC算法的控制效果更好,鲁棒性更强。
5 结 语
针对DAB变换器在传统PI控制下动态响应慢、鲁棒性差,以及传统MPC控制参数依赖性问题,本文提出LESO-MFPC控制策略。该方法将超局部模型与预测控制相结合,同时,设计LESO对超局部动态部分进行估计并补偿,较大降低了系统对模型参数的依赖性,无需精确建模便具备良好的控制性能。最后,设置PI-MPC算法作为实验对照,多种工况下实验结果均验证所提LESO-MFPC算法具备更好的动、稳态性以及更强的鲁棒性。

