浸入运动边界-格子Boltzmann方法4种固含率计算方法对比研究*

夏 明，邓柳泓，黄刚海，徐远臻

(1.湘潭大学 岩土力学与工程安全湖南省重点实验室，湖南 湘潭 411105；2. 中南大学 土木工程学院，湖南 长沙 410075；3. 西南交通大学 交通隧道工程教育部重点实验室，成都 610031)

0 引言

格子Boltzmann方法(LBM)[1-2]是一种基于流体微观模型和介观动理论的数值方法，它视流体为离散粒子集合体，通过离散粒子的碰撞和迁移来实现流体流动的.LBM具有粒子方法的背景，能方便地模拟流体和固体颗粒的相互作用，流固耦合[3-4]模拟比传统方法有优势.

关于LBM流固耦合边界的处理，过去30多年已形成几种方法.Ladd[5-6]在1994年提出修正的反弹格式法(LBB)用于模拟颗粒悬浮问题，当颗粒速度较大时，LBB会产生数值振荡.为克服该数值振荡，随后Chun等[7]提出了插值反弹边界方法(IBB)，但该方法在固体边界处有时不能满足无滑移边界条件.Feng等[8]引入浸入边界法[9](IBM)处理流固耦合边界，其基本思想是采用独立的两种网格，即欧拉网格和拉格朗日网格，分别模拟流场和固体边界；IBM用动量交换法计算流固作用力，这种显式求解流体力的做法无法完全满足无滑移边界条件.之后一些学者提出了流体力隐式计算方法[10]，但需要复杂矩阵运算和较高计算内存要求，且高雷诺数的流动模拟中易出现流体力计算振荡[11].Noble等[12]提出的浸入运动边界法(IMB)克服了其他耦合方式动量不连续的问题，在较低分辨率网格下能够提供具有足够代表性的网格非一致边界.IMB引入格子固含率和附加碰撞项修正LBM方程，保留碰撞算子的局部性和迁移操作的简单性，其计算流体力更加平顺，是一种非常适合流固耦合的数值方法，因而被运用到诸多现象的模拟[13-14].

在用IMB法实现LBM流固耦合时，需要引入一个新的物理量，即固含率.所谓固含率，是指被固体覆盖的格点单元比例.固含率是IMB法修正LBM方程的重要参数.在固体内部，固含率是1；在纯流体格点，固含率是0；在边界点，固含率为固体占据格点格子控制体的面积，因此固含率在0和1之间.在处理流固耦合格点时，需要精确地算出每一个被颗粒覆盖格点的固含率.固含率的计算方法通常有4种，即蒙特卡洛法(MCM)、单元分解法(UDM)、近似多边形法(APM)和闭合边界法(CBM).这些方法在理论上各有优劣，但它们的精度和耗时的衡量标准鲜有研究.本文针对常见固含率计算方法的精度和耗时做系统地测量，为优选固含率计算方法提供借鉴.

1 浸入运动边界-格子Boltzmann模型

二维问题常采用D2Q9模型[15]进行数值模拟，不考虑外力项的LBM方程为：

(1)

式中：fa(r，t)为格点的分布函数；r为格点坐标；ea为速度的离散方向；δt为时间步长；t为当前时间；τ为无量纲松弛时间；feq为速度空间的局部平衡态分布函数.

式(1)各变量的取值如下：

(2)

式中：c=δx/δt，其中δx和δt分别表示网格步长和时间步长，通常x和y方向的网格步长相同，为便于统一计算，一般取δx=δy=1.

(3)

IMB法处理流固耦合边界时，被颗粒覆盖的格点LBM方程变为：

(4)

(5)

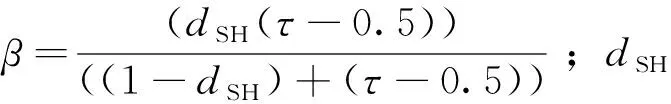
对比式(1)和式(4)可以看出，用IMB法修正受颗粒影响的格点LBM方程本质上是在方程右边加入固含率和附加碰撞项.

2 固含率计算方法

2.1 格点固含率

二维问题的固体颗粒常用圆盘表示，因而本文以圆盘颗粒展开固含率计算方法的论述.

如图1所示，流场被划分成格子，格子控制体为4个格子中心围成的区域，格点固含率为格子控制体中固体区域所占百分比.如图2所示，流场格点分为4种，正常格点(不在固体内部且任何方向不与固体格点连接)、固体内部格点(在固体内部且任何方向不与流体格点连接)、固体边界格点(在固体内部且某一方向与流体格点连接)和流体边界格点(不在固体内部且某一方向与固体格点连接).正常格点按式(1)进行碰撞迁移，无须计算固含率；固体内部格点按式(4)和式(5)进行碰撞迁移，但其固含率为1，无须额外计算；固体边界格点和流体边界格点也按式(4)和式(5)进行碰撞迁移，该两类格点固含率在0和1之间，需要专门计算.由于格子控制体的面积是1，因此就图2中的格子控制体(a)和(b)，它们的固含率实际上就等于阴影部分的面积.

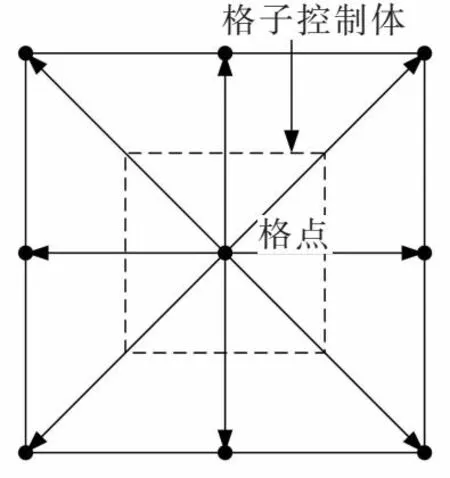
图1 格子控制体示意图Fig.1 Schematic diagram of lattice control body

图2 计算域中的四种格子控制体示意图Fig.2 Schematic diagram of four lattice control body in computational domain

2.2 固含率4种计算方法

假设边界格点坐标为(dx，dy)，下面阐述常用的4种边界格点固含率计算方法.

2.2.1 蒙特卡洛法

该法利用统计思想计算格点固含率.在格点的格子控制体内，用随机数生成一系列随机点，固体区域内部的随机点数与随机点总数的比值即为格点固含率.MCM计算固含率步骤如下：

1)利用线性同余法分别生成x、y两组随机数组合成随机点坐标.

先在区间[0，1]，生成均匀分布的随机数，线性同余法的递推公式为：

(6)

式中：M=2 147 483 648；p=314 159 269；q=453 806 245；X0取以系统时间为种子的随机正整数；mod(M)表示对M取余；Rn为产生的随机数.

为了得到很好的伪随机数，M取值是整数型的最大值；p和q必须足够大，且不相等.

利用下式的抽样公式，可生成区间[a，b]均匀分布的随机数.

t=a+(b-a)R，

(7)

式中：R为区间[0，1]生成的随机数；t为区间[a，b]生成的随机数.

x坐标对应的区间为[dx-0.5，dx+0.5]，y坐标对应的区间为[dy-0.5，dy+0.5].

2)判断生成的点与固体颗粒的位置关系.

假设生成的随机点坐标为(dxm，dym)，圆盘的圆心坐标为(dCx，dCy)，半径为r，则位置关系的判断式为：

(8)

3)采用式(9)计算格点固含率.

(9)

式中：iNum为位于圆盘颗粒内部的随机点数量；iTotal为随机点总数.

2.2.2 单元分解法

UDM与MCM类似，只是把随机点换成子单元进行统计，其具体步骤如下：

1)把格子控制体划分成边长为1/n的n2个正方形子单元，第i列j行的子单元中心坐标为：(dCx-0.5+(i+0.5)/n，dCy-0.5+(j+0.5)/n)；

2)判断子单元中心与固体颗粒的位置关系，判断公式同式(8)；

3)按式(9)计算固含率.

2.2.3 近似多边形法

如图3所示，边界格点有5种可能情况，情况①～情况⑤的格子控制体依次有1个、2个、3个、4个和0个顶点位于圆盘颗粒内部.APM将位于格子控制体内部的圆弧线视为线段，即认为格子控制体被分割为2个多边形.此时，图3中5种情况的固含率依次为：

(10)

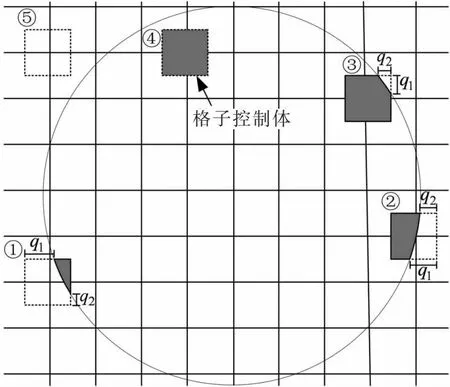
图3 APM示意图Fig.3 Schematic diagram of APM

式中：q1和q2的含义如图3所示，具体为被圆弧切割的格子控制体棱边位于圆盘外部的长度.

下面讲述q1的计算方法，q2的计算与q1相同.

先找到颗粒内部的顶点和与之相关的外部点.如图4所示，假设找到的内部点和外部点分别为B(x2，y2)和A(x1，y1)，圆盘圆心为O(dCx，dCy)，圆盘半径为r，点C为OA与圆弧的交点，点D为AB和圆盘边界的交点，则q1为图中AD的长度.由余弦定理得：

(11)

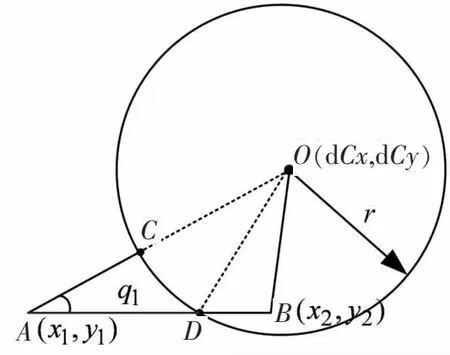
图4 q1计算示意图Fig.4 Schematic diagram of calculating q1

令OA=a，AB=b，OB=c，OD=r，则有

(12)

将式(12)代入式(11)，可求得两根为：

(13)

式中：φ=a2+b2-c2.

因点D位于A和B之间，且AB=1，所以式(13)的两个解只有满足0≤q1≤1才是正解.

2.2.4 闭合边界法

如图5所示，采用CBM时，位于格子控制体内的圆弧被视为真实圆弧，因而该法可求出准确的固含率.由此可以看出，CBM的固含率就是由APM算出的固含率加上图5中弓形的面积，即S1+S2.

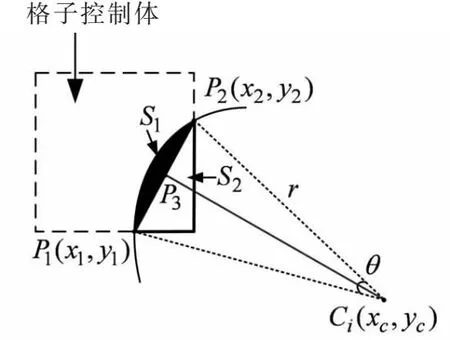
图5 CBM示意图Fig.5 Schematic diagram of CBM

下面讲述图5弓形面积S1的计算方法.

通过式(13)易算出圆弧与格子控制体的两个交点坐标p1(x1，y1)和p2(x2，y2)，假设圆盘半径为r，则三角形CiP1P2和扇形CiP1P2的面积计算式为：

(14)

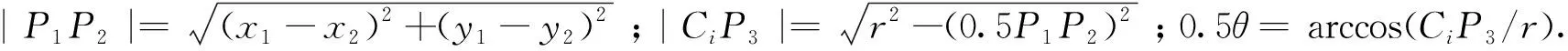
弓形面积S1=S扇CiP1P2-SΔCiP1P2.

3 精度和效率测试

3.1 精度测试

3.1.1 随机点数的确定

由固含率4种计算方法的计算步骤可看出，MCM和UDM的计算精度与随机点数和子单元数有关.因此，本文分别测试不同圆盘直径下随机点数和子单元数对计算精度的影响，达到优选随机点数和子单元数的目的.测试模型：流场格子数为2 000×2 000；测试圆盘圆心坐标为(1 000，1 000)，直径分别为10、20、100、200、400、600、800、1 000和1 200；相应测试的格子控制体中心坐标分别为(995，1 000)、(990，1 000)、(950，1 000)、(900，1 000)、(800，1 000)、(700，1 000)、(600，1 000)、(500，100)和(400，1 000).CBM算出的准确固含率分别为0.491 654、0.495 832、0.499 167、0.499 583、0.499 792、0.499 861、0.499 896、0.499 917和0.499 931.采用MCM和UDM分别计算上述格点固含率10次，所用随机点数和子单元数依次为100、400、900、1 600、2 500、3 600、4 900、6 400、8 100和10 000，经测试得：1)MCM的误差不受直径的变化影响，只与随机点个数有关，10组图的结果几乎完全一致；如图6所示，误差随随机点数的增加而降低，但随机点数为2 500时曲线会有转折，当随机点数大于400时，误差稳定在1%及以下，最终误差稳定在0.4%～0.5%；2)UDM的误差随直径的增大而降低，图7(a)和图7(b)给出了直径分别为10和20时的计算误差，其余模拟工况随直径的增大误差不再变化，均在0.1%以下.UDM计算精度高，子单元数大于100可使误差稳定在1%以下.

图6 MCM误差结果图Fig.6 The error of MCM

图7 UDM误差结果图：(a)直径为10；(b)直径为20Fig.7 The error of UDM：(a) r=10；(b) r=20

为了探究格子控制体被圆弧切得的形状对MCM和UDM计算精度的影响.测试了在圆盘直径为20时，每一个边界格点的固含率误差.发现随机点数大于1 000和子单元数大于100时，每个边界格点的固含率计算误差稳定在2%左右.因此，下面测试选取的随机点数为1 000，子单元数为100.

3.1.2 圆盘大小对精度的影响

为研究圆盘大小对4种计算方法计算固含率精度的影响，进行如下测试.测试工况与第3.1.1节一致.将各种模拟工况下各边界点固含率的误差值进行统计，采用平均值Er2表征，即：

(15)

式中：Xi(i=1，2，3，…，n)为第i个边界点的固含率绝对误差值(剔除绝对误差为0的边界点)；n为参与统计的边界点数.

各种测试工况的Er2值如图8(a)所示，从中可知：1)除APM外的3种方法，Er2值不受影响；原因在于，CBM误差总是0，MCM与UDM均采用统计方法求解固含率，其求解结果不受格子控制体形状影响；2)APM的误差随圆盘半径增大而减小；这是因为APM的误差为图5中弓形的面积S1，当圆盘颗粒增大时，S1逐渐减小.应该指出，即便圆盘直径仅为10倍格子长度，APM的计算误差也仅为0.44%，表明APM容易达到很高的计算精度.

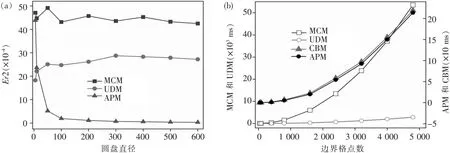
图8 (a)固含率计算误差；(b)固含率计算耗时Fig.8 (a)Solid ratio calculation error；(b)The time consumption of solid ratio calculation

3.2 精度测试

3.2.1 单个圆盘模型

记录“3.1小节”下“3.2.1小节”各种测试工况的耗时(测试计算机为Intel(R) Xeon(R) CPU E5-2640 v3×2 @2.60 GHz、64G内存、2T硬盘)，结果如图8(b)所示.为体现不同计算规模下4种计算方法的效率，将图8(b)的横坐标变成边界格点数.从图8(b)可以看出：1)APM和CBM效率比MCM高约2个数量级，比UDM高约1个数量级；原因在于，APM和CBM仅采用简单的运算来求解固含率，因而计算效率高；而MCM和UDM需耗费时间生成随机数和子单元，导致效率降低；2)APM计算效率较CBM高；这是因为CBM需多计算图5中弓形的面积S1；3)UDM的效率比MCM高约1个数量级；原因在于UDM用少量的子单元可以达到大量随机数的计算精度，子单元数小于随机点数，因而计算效率高.

3.2.2 多颗粒沉降流固耦合模拟

为研究固含率计算方法在LBM流固耦合计算中的作用，本节将LBM与圆盘颗粒非连续变形分析方法(DDDA)进行耦合，分别用4种方法计算每种模拟工况的固含率，统计固含率计算环节的耗时.DDDA的基本原理参见参考文献[16]和[17].如图9所示，流固耦合模型模拟的是密闭方腔的多颗粒自由沉降，方腔尺寸为0.02 m×0.02 m，每个流体格子的真实物理长度为0.000 396 5 m，对应格子区域为512×512；颗粒直径为0.000 5 m，LBM松弛因子为0.991 5，颗粒和流体密度分别为1.01 g/cm3和1.0 g/cm3，流体计算时步为0.000 25 s，DDDA计算时步为0.000 5 s，1步固体计算对应2步流体计算，分别用10、20、40、60、80和100个圆盘进行颗粒自由沉降模拟.圆盘颗粒生成可采用文献[18]提出的高效算法，该算法可在0.9 s内生成410万颗粒.

图9 流固耦合测试模型Fig.9 The test model of fluid-solid coupling

图10给出了各种流固耦合模拟工况下4种方法计算固含率的耗时.从图可以看出：1)APM和CBM的计算效率比MCM高约2个数量级，比UDM高约1个数量级；2)CBM效率略小于APM；3)UDM计算效率比MCM高约1个数量级.总体上看，4种计算方法的效率排序为：APM>CBM>UDM>MCM.

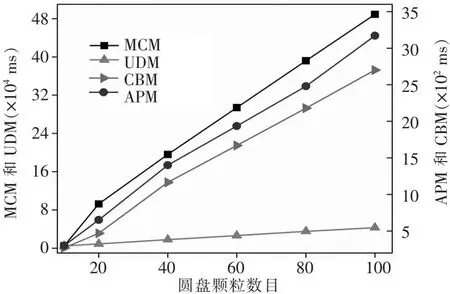
图10 流固耦合计算耗时Fig.10 The time consumption of fluid-solid coupling

4 结论

1)MCM和UDM取1 000和100左右的随机点和子单元时可保证固含率计算精度，此时误差小于1%.

2)APM容易达到较高计算精度；当圆盘直径大于10倍格子长度时，APM的计算误差小于0.44%.

3)APM和CBM的计算效率比MCM高约2个数量级，比UDM高约1个数量级；CBM效率略小于APM；UDM比MCM计算效率高约1个数量级.4种计算方法的效率排序为：APM>CBM>UDM>MCM.

4)用浸入运动边界法进行DDDA-LBM流固耦合时，格点固含率计算应采用APM，当计算精度要求很高时应采用CBM.