基于CNN-LSTM混合神经网络的高速铁路地震响应预测*

张学兵，谢啸楠，王 礼，吴 晗

(湘潭大学 土木工程学院，湖南 湘潭 411105)

0 引言

为满足行车安全性和舒适性，高速铁路桥梁梁体与桥墩往往具有较大刚度和较高基频，在地震发生时常受到较大的地震作用，甚至在罕遇地震作用下仍表现出较好的抗震性能.无砟轨道为高速铁路简支梁桥提供一定的纵向约束，提高了桥梁整体性，使相邻跨的简支梁成为存在一定耦合的连续结构[1].CRTS Ⅱ是中国无砟轨道的一种典型的结构形式，针对铁路桥梁比例高、长桥多的特点而设计并先后应用于京津、沪杭、京沪等铁路中[2-3].近些年来，中国高速铁路产业发展迅速，在山区的地震断层区、沿海地区的高地震烈度区以及西部地震多发区的建设有所增加[4].为保证行车安全，研究其在地震荷载作用下的桥梁反应具有重要的理论意义和工程实用价值[5-7].

为研究其抗震性能，Yan等[8]建立简支梁桥和CRTS Ⅱ轨道的三维非线性动力学模型，研究了其在不同地震激励强度下的受力和变形特征.结果表明，钢轨、轨道板和底板的峰值应力均发生在桥台或锚固件处.Montenegro等[9]研究出中等烈度地震可能不会对结构造成重大破坏，可以在弹性域分析.Guo等人[10-11]建立了CRTS Ⅱ轨道结构有限元模型以研究各构件的地震破坏机理，并提出了一种有效的简化桥梁轨道模型模拟轨道结构对桥梁纵向约束的影响.Li等[12]采用概率密度演化法对高速铁路轨桥耦合系统随机地震响应进行了研究，从随机角度评价轨道结构的抗震性能.

而振动台试验方法可以在实验室准确再现结构相应的地震震动，是抗震试验方法的重要组成部分[13]，Jiang等[14]通过对高铁连续梁桥进行试验，研究了不同地震烈度和加载方向对结构地震反应的影响，并分析其损伤状况.Yang等[15]在一个1/6比例的桥梁模型上进行了一系列振动台试验，以研究碰撞对桥梁模型横向地震响应的影响以及橡胶缓冲器的减震效果.本文也基于振动台试验研究桥梁地震响应.

近些年，在现有的基础设施上，使用光纤布拉格光栅(FBG)传感器进行结构健康监测的情况正在逐渐增加.Wang等人[16-18]将光纤传感技术应用在沥青路面全尺寸以及多层沥青路面结构性能现场监测中，验证了其良好性能并且基于应变传递分析提高了光纤传感器的耐久性.Zhang等[19]利用光纤光栅传感器对非对称钢筋混凝土剪力墙结构在渐进地震荷载作用下的损伤响应进行监测.在桥梁方面，Lu等[20]采用外贴光纤光栅应变传递器研究车辆荷载作用下大跨度刚构桥长标距应变计的动、静态应变分离方法，并从动态应变信号中提取有效的准静态应变分量.Zhao等[21]基于光纤温度传感器监测数据构建了列车-桥梁动力学模型，分析了主梁的温度变形对列车引起的梁挠度的影响.基于已有在工程上运用光纤光栅检测的实例，本文基于光纤光栅波分复用技术[22]在单根光纤上串联多个FBG传感器从而实现准分布式光纤光栅传感系统[23-24]，将串联好的光纤光栅贴在缩尺CRTS Ⅱ轨道模型上，从而实现长距离多点采集.

大数据、机器学习以及人工智能等新兴技术兴起，已运用至多领域中.例如，徐博文等[25]提出一种深度学习算法模型，用以对麦穗进行识别监测.王虎等[26]建立了一种神经网络预测模型，辅助人汽车驾驶.赵星宇等[27]提出一种混合神经网络模型，实现对文本情感的实时分析.机器深度学习为桥梁抗震减震理论与技术研究提供了新思路和新途径.近年来，人工神经网络(ANN)已被证明具有卓越的非线性函数建模能力[28]而被广泛用于预测结构地震反应[29-31]、损伤状态[32-33]、失效模式[34]等，并在预测结构地震反应方面评估结构抗震性能[35]、损伤状态[36]等.随着对神经网络的深入研究，有学者开发了一维卷积神经网络(1D-CNN)与长短期记忆(LSTM)网络来预测地面结构地震反应的时间序列[37-38].为了提高神经网络地震应变响应预测精度，本文提出了一种CNN-LSTM 网络混合模型.它结合了CNN和LSTM网络的各自特点，利用准分布式光纤光栅采集地震作用下简支梁桥的应变，将所测光栅位置、地震方向、峰值加速度按时间滑动窗口构造连续特征图作为输入，因所测光栅处于同一根光纤中，所在地震时程曲线相同的条件下，利用其余6个光栅点所测得应变响应进行深度学习从而预测跨中应变.该深度学习模型使用CNN提取特征图中连续和非连续数据之间的关系，形成特征向量.然后将特征向量构造成时序序列并输入到LSTM网络中进行响应预测.相较于仅使用LSTM网络模型，CNN-LSTM混合模型在提高预测准确率方面具有优势.因为该模型使用CNN模型提取时序数据的潜在特征，并将其作为LSTM网络的输入数据，从而提供大量的有效输入数据.

1 数据采集与处理

通过在振动台系统上搭建缩尺简支梁桥[5]，分别在缩尺桥梁跨中段的轨道板布设准分布式光纤光栅，用以监测同一直线不同方位的应变响应.

1.1 地震台实验装置

本文以CRTS II板式无砟轨道系统的多跨简支梁为研究对象，以1∶10的相似比建立桥梁的缩尺模型，构建基于4列震动台的桥上运行试验平台.

原型以中国高速铁路简支箱梁实桥为研究对象，跨度为32.5 m的混凝土简支箱梁桥，桥墩为圆柱形实心桥墩，高度范围为3 ～20 m.高度小于14 m的桥墩为等截面桥墩，高度大于14 m的桥墩为变截面桥墩，坡度为1∶45.防落梁装置的触发间距为20 cm.使用盆式橡胶支座，其最大垂直和水平承载力分别为500 0 kN和100 0 kN.聚四氟乙烯板具有低摩擦系数，可用于实现屋顶和底盆之间的相对运动.橡胶在三维应力作用下具有流动性，可用于实现主梁的转动.密封圈用于将橡胶与空气分离，以延缓老化.

该轨道为CRTS II板式无砟轨道系统.箱梁与底板之间铺设滑动层以释放轨道结构的温度应力，而底板与轨道板之间铺设CA砂浆层作为缓冲层.钢轨与轨道板采用紧固件连接；在固定支座上方的箱梁表面设置剪切槽，以限制底板的移动；在梁缝两端底板与轨道板之间设置抗剪钢筋，以减小梁角对轨道变形的影响；在底板和履带板两侧设置横向挡块，以限制其横向移动.紧固件和挡块的布置间距分别为0.65 m和6.5 m.

模型装置如图1所示.缩尺桥梁为钢结构桥梁，缩尺比例为1∶10，每跨长3.25 m，共11跨.表1列举了模型相似系数.试验选取两种正弦波地震激励，参数见表2所示.地震频率为10 Hz，峰值加速度分别为0.1g、0.2g.为了便于安装，全桥材料采用钢材；扣件使用钢板；钢轨、轨道板、底座板、梁和桥墩基于等效弯曲刚度制作；剪切钢筋、剪力齿槽、侧向挡块和支座根据等效力和位移原理，对不同尺寸的试件进行实验，根据实验结果选择最合适的尺寸；滑动层材料与原型相同；CA砂浆层用聚氨酯代替.振动台试验系统由1个4 m×4 m六自由度固定台和3个4 m×4 m六自由度移动台所组成，台阵间距可在 6～25 m之间调整.

表1 缩尺模型相似系数

表2 正弦波地震激励参数

图1 模型装置图Fig.1 Device model diagram

1.2 光纤光栅数据采集装置

本节主要详细介绍用以监测振动台下缩尺桥梁地震应变响应的光纤光栅数据采集装置.

在缩尺桥梁跨中段的轨道板、钢轨、底座板、钢轨上分别使用环氧树脂粘贴1根光纤，光纤刻有7个光栅点，光纤布置如图2所示.将刻有7个光栅点的光纤按第4个光栅点对应桥梁跨中中间位置粘贴在轨道板上，保证光栅点能均匀分布在所监测结构上.数据采集图和示意图分别如图2和图3所示.

图2 FBG布置图：(a) 光纤粘贴位置；(b) 光栅点；(c) 箱梁上的光纤；(d) 测试模型和解调系统Fig. 2 FBG arrangement diagram：(a) Fiber optic paste position；(b) Grating point；(c) Fiber optic of beam；(d) Test model and demodulation system

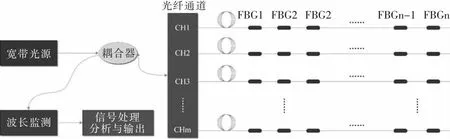
图3 数据采集示意图Fig.3 Schematic diagram of data acquisition

2 卷积神经网络和长短期记忆网络的响应预测模型

CNN-LSTM模型组合了CNN和LSTM网络两种模型，先采用CNN提取特征向量，将特征向量以时序序列方式构造并作为LSTM网络输入数据，再采用LSTM网络进行响应预测.将CNN模型提取出的深度特征时间序列使用LSTM网络模型进行训练.整个过程可以分为数据前处理和模型训练两个阶段.

2.1 卷积神经网络

CNN通过卷积运算和池化操作，减少网络参数数量的同时，保留了多维数据的深层特征，其架构由卷积层、池化层和完全连接的层组成.下面介绍有关这些不同层的相关信息.

1)卷积运算

卷积层和非线性激活函数通过卷积运算来计算输入和输出，计算过程展示如下：

yi=σ(ki×x+bi)，i=1，2，…，K.

(1)

式中：x为宽度W1、高度H1和深度D1卷积层的输入；ki为第i个卷积滤波器，其尺寸为F×F×D1；bi为卷积滤波器ki的第i个偏差；σ为非线性激活函数；yi为与第i个卷积滤波器对应的第i个输出矩阵.每层有K个卷积滤波器.卷积运算在图4卷积神经网络的卷积运算进行了演示，该卷积使卷积过程的步幅为S=1.对于第i个卷积过程yi的输出，宽度为W2，高度为H2，深度为卷积核的个数K.第i个输出矩阵中的每个元素都是由输入矩阵和第i个卷积滤波器ki点积计算得出的.

(2)

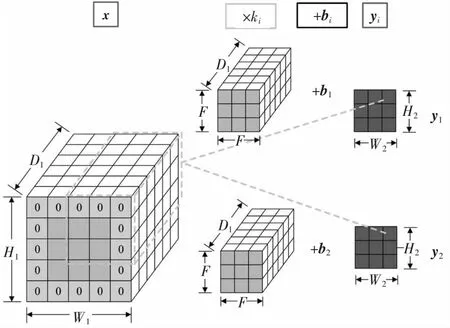
图4 卷积神经网络的卷积运算Fig.4 Convolutional operation of convolutional neural network

通过在输入矩阵周围填充0，可以调整输出矩阵的大小.通常，当跨度为S=1时，将每一侧的填充零数设置为P=(F-1)/2，可以确保输入量和输出量在空间上具有相同的大小.在图4卷积神经网络的卷积运算中，一层零插入到原始输入矩阵的每一边周围.因此，输出的宽度W2和高度H2可通过上式计算.

2)池化和全连接层

池化操作是一个下采样过程，它从相应采样窗口中提取某个属性(例如最大值，平均值和L2-范数)作为低维输出.以最大池化为例，池化层的下采样操作如图5卷积神经网络的池化运算所示.在池化窗口中取最大值的过程是在输入深度维度上的每个切片上独立进行的，因此输出矩阵的深度尺寸与输入矩阵相同.此外，输出矩阵的宽度和高度也可以通过与卷积层中相同的方法来计算，并且步幅通常与池化窗口的宽度或高度相同.

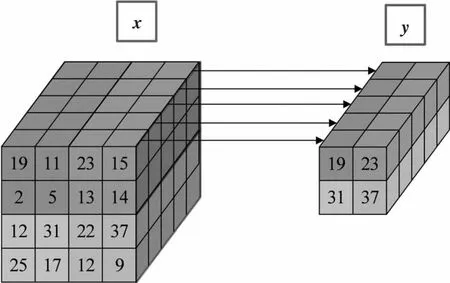
图5 卷积神经网络的池化运算 Fig.5 Pooling operation of convolutional neural network

2.2 长短期记忆网络

LSTM网络是一种改进的时间循环神经网络(RNN).它被提出后也进行了改良，增加了额外的遗忘门.其网络基本单元如图6所示.

图6 LSTM神经网络基本单元Fig. 6 Basic unit of LSTM neural network

LSTM网络的基本单元包括3个门控单元，分别为遗忘门、输入门和输出门.遗忘门中的输入xt与状态记忆单元St-1以及中间输入ht-1共同作用来决定哪些信息需要遗忘.输入门中的xt两个输入分别通过sigmoid函数和tanh函数进行变换，共同作用于状态记忆单元，以确定哪些信息需要被保留.中间输出ht是由更新后的状态记忆单元St与输出ot共同作用决定的.

2.3 CNN-LSTM网络混合模型

2.3.1 本文模型结构与参数配置

本文提出的CNN-LSTM网络混合模型结构如图7所示，由17个堆叠的功能层构成，CNN-LSTM网络混合模型主要由两部分组成，CNN网络主要负责特征提取，LSTM网络主要负责负荷预测.CNN具体模型参数如表3所示.模型使用Python中的scikit-learn机器学习库和PyTorch框架进行实现.该模型是以时间序列特征图作为网络的输入.光栅位置信息、地震波类型、监测时间等数据实际上都是相互独立的时间序列.为了耦合这些影响负荷的特征信息，本文参考自然语言处理中的词向量表示方法，将某一时刻的负荷值与其相关的特征串联成向量表示，进而形成一个全新的时间序列数据.每一时刻的历史负荷均与其相关的特征共同表示.然后再使用滑动窗口方式依次将输入的时间序列数据生成特征图，为了方便后续网络计算，滑动窗口宽设为30 000条记录，单位特征图的尺寸为30 000×6.模型设有5层卷积层，各卷积层尺寸及步长等信息如表3所示.

表3 CNN网络架构详细配置

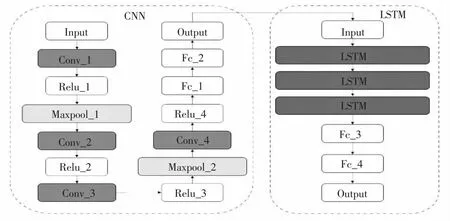
图7 CNN-LSTM模型Fig.7 CNN-LSTM model

输入的子序列首先放入Block1中处理.Block1有3个功能层，依次包括卷积、ReLU和池化.它们在图中分别表示为Conv_1、ReLU_1、Maxpooling_1.第一层Conv_1的输入大小为30 000×1×30，卷积层由32个卷积核组成，卷积核的大小为1 000×1×30，滑动窗口的步长为100.ReLU层对输出尺寸没有影响.池化层尺寸为2×1×32，步长为2.因此，Block1的输出尺寸为146×6×32.在该模型中，卷积层用于提取输入样本的区别特征.选择5个卷积层是基于LeNet-5在分类识别方面的成果[39-40].

2.3.2 实验评价指标

预测结果评估是为了验证CNN-LSTM模型的预测精度，分别使用根均平方误差(RRMSE)、平均绝对误差(RMAE)和决定系数(R2)来对模型预测结果进行统计.下面进行详细介绍.

(3)

(4)

(5)

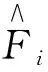
RRMSE和RMAE两个指标都是用来描述预测值与真实值的误差情况.它们之间的区别在于，RRMSE先对偏差做了一次平方，这样的话，如果误差较大，RMAE放大了误差.决定系数R2用于评价模型的平均预测精度，是总误差的平方和与总偏差的平方和之比.RRMSE和RMAE结果越接近0，R2的结果越接近1，模型的预测精度就越高.

3 实验结果分析

本次实验采用控制变量法逐步进行模型调整，旨在测试增加LSTM网络层数对模型预测效果的影响.在固定CNN层提取特征的情况下，通过不断增加LSTM网络的层数，测试了模型深度的影响.实验结果如表4所示，其中列出了7个评价指标的平均值.从实验结果可以发现，适当增加LSTM网络层数可以提高模型预测能力.然而，当LSTM网络层数增加到4层以上时，误差率升高，表明发生了过拟合.因此，本次试验选择了3层LSTM网络作为最终模型.

表4 LSTM网络层数对轨道板预测结果精度的影响

图8是中间光栅点算法模型预测值与实际值的比较，从图8(a)～图8(f)中可以看出，对于不同地震激励下的应变响应，在没有给出特定时间点的地震时程曲线谱的情况下，CNN-LSTM模型仍然可以通过同一时刻其他位置的光栅应变响应而得出另一位置的应变信息，尽管在峰值处的拟合数据相对差异较大，但总体符合地震动的变化趋势，与实际变化趋势基本一致.对于图8(g) 和图8(h) ，可以明显看出本文提出的深度学习模型在轨道板、钢轨、底座板的适用性比箱梁处好，从光栅预设位置猜测可能是箱梁离其余位置较远，该模型依托于轨道板应变数据而搭建的，钢轨、底座板与轨道板距离很近，所以效果比较好，而箱梁距离轨道较远并且是地震激励的主要承受位置，使得与其他地方的应变不同，从而导致箱梁的预测效果较差.CNN-LSTM模型优越性的原因可以从两个方面考虑.首先，它归因于自动编码器的“降维”.对于当前关于地震应变响应的预测问题，由于应变大小应在同一时刻相近位置之间逐渐变化而不是突然变化，因此高维输入特征之间存在多重共线性.然而，通过自动编码器，高维输入可以转换为低维的潜在表示.这种嵌入向量保留了原始输入的基本特征，同时减轻了特征之间的相关性.同时，它的降维有助于减少回归器中未训练参数的数量，这有利于训练过程的收敛，节省计算预算，提高运算效率.其次，CNN可以通过使用多个小型卷积滤波器从各个位置的应变图中逐步提取局部分布，从而充分利用区域信息.同时，池化层每次只保留主要特征，可以减少噪声传输.

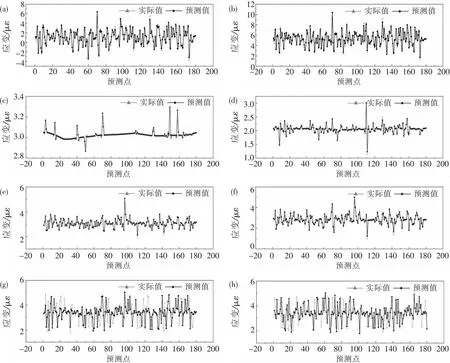
图8 模型预测值与真实值的比较：(a)PGA=0.1g，轨道板光栅应变预测结果；(b)PGA=0.2g，轨道板光栅应变预测结果；(c)PGA=0.1g，钢轨光栅应变预测结果；(d)PGA=0.2g，钢轨光栅应变预测结果；(e)PGA=0.1g，底座板光栅应变预测结果；(f)PGA=0.2g，底座板光栅应变预测结果；(g)PGA=0.1g，箱梁应变预测结果；(h)PGA=0.2g，箱梁应变预测结果Fig.8 Comparison of model predicted values and true values：(a)PGA=0.1g，track plate grating strain prediction results；(b)PGA=0.2g，track plate grating strain prediction results；(c)PGA=0.1g，rail grating strain prediction results；(d)PGA=0.2g，rail grating strain prediction results；(e)PGA=0.1g，base plate grating strain prediction results；(f)PGA=0.2g，base plate grating strain prediction results；(g)PGA=0.1g，box beam strain prediction results；(h)PGA=0.2g，box beam strain prediction results

4 结论

本文针对高速铁路简支梁桥振动台试验模型，在轨道板、底座板、钢轨、箱梁处布置准分布式光纤光栅监测应变，提出了一种基于CNN-LSTM模型的地震响应预测方法，该方法利用CNN处理数据，提取有效特征，再通过LSTM网络进行时序数据分析.该方法有以下优势：

1) 将多源数据按时间滑动窗口构造连续特征图作为输入，充分发挥CNN模型的特征提取优势，从而挖掘数据中蕴含的更多有效信息. 将特征向量以时序序列方式构造并作为LSTM网络模型输入数据，LSTM网络模型能较好地拟合响应数据的时序性和复杂的非线性关系；

2)本文提出的CNN-LSTM模型充分发挥了CNN模型和LSTM网络模型的优点.经过全面的分析研究和验证，本文证明了该模型的有效性.针对RRMSE、RMAE、R2等几个评估指标，本文发现，与单一模型相比，采用两种模型结合的融合模型在特征表达方面更加有效，预测精度更高；

3) CNN-LSTM模型可以很好地实现光纤光栅对桥梁地震响应的预测，所使用的网络模型适用于大部分点位；

4)光栅因自身材质问题不易存活或出现测量点应变突变等情况，通过本文的研究发现利用深度学习可以通过已测光栅点的应变信息预测其他点的应变.从一定程度上可以减少监测成本及避免因光栅不成活而造成的数据损失.