基于信道模型的短波时差测量克拉美罗界分析*
王君明,周 晨,李 琛,吕明杰,乔 玮,朱建桦
(武汉大学 电子信息学院,湖北 武汉 430072)
0 引言
时间延迟测量(估计)是现代信号处理中信号检测和参数提取问题的一个重要组成部分,广泛应用于雷达系统、通信系统等领域[1]高精度时差的提取,是短波时差定位的前提.时差测量可以分为两类[2]:第一类为直接法时差测量,它通过直接记录信号到达各空间分离观测站的时间来计算到达不同位置观测站的时间差,该类方法仅适合一些高频脉冲信号;第二类为间接法时差测量,它通过空间分离的观测站截获信号,通过特定的时延估计算法来计算不同观测站所截获信号间的时差关系,间接法时差测量使用时延估计算法来测量时差,时差测量精度较高.
电离层是受太阳高能辐射以及宇宙线的激励而电离的大气高层.电离层从离地面约0 km开始一直伸展到约1 000 km高度,地球高层大气空域中存在相当多的自由电子和离子,能使短波改变传播速度,发生折射、反射和散射,产生极化面的旋转并受到不同程度的吸收[3].由电离层运动产生的多普勒频移[4]、电离层的时空变化[5]、电离层的信道时延等因素将直接影响时差测量的误差.因此,不得不依赖电离层模型来模拟电离层的影响,电离层模型能够体现电子浓度在竖直高度上分布的规律.按模拟方法可将电离层模型分为理论模型、经验模型和半经验模型3种,国际参考电离层(IRI)模型[6]、NeQuick模型[7]等是电离层领域中常用的经验模型.
已经进行了大量的研究来估计时差测量的精度.Helstrom[8]、Woodward[9]和Wahlen[10]提出了有源系统的时间延迟误差的方差.Knapp等[11]根据相干函数显示了时间延迟估计的方差.但以上都为视距下信号传播的时差估计克拉美罗界(CRLB),短波信号经过电离层传播,必然受到电离层的调制作用,从而影响短波信号时差估计的CRLB.Bell等[12]提出经典的匹配滤波技术,克服了多径效应引起的传统时延估计算法性能下降的问题,但是仍存在算法分辨率不高的问题.Ge等[13]将多径环境下的时延估计转化到频域,利用多重信号分类方法(MUSIC)实现超分辨率多径时延估计,但方法局限于窄带信号.张阳等[14]在Watterson短波信道模型的基础上,提出了基于广义相关熵的时延估计算法,在较低信噪比下也能保持较高的时延估计性能,但基于模型的限制,同样只适用于窄带信号.Yang等[15]基于准抛物模型,采用解析性射线追踪建立了短波时差测量方程并讨论了对定位的影响,但在电离层变化较为复杂的情况下,量化参数(QP)模型的适用性还有待研究.基于上述不足,本文考虑了电离层水平相关性的影响,利用IRI模型构建了宽带短波信道.
本文第一节基于IRI模型,采用数值型三维射线追踪的方法构建了Vogler宽带短波信道模型,并给出了时延和多普勒频移等参数估计.第二节给出了在Vogler信道模型下的时差测量模型,并推导了时差测量估计的CRLB.第三节给出了Vogler短波信道的散射函数仿真结果与不同条件下时差测量CRLB的仿真结果.最后,在第四节进行总结,评估了影响时差测量CRLB的因素.
1 Vogler信道模型
短波经过电离层传播产生的多普勒效应和多径效应分别引起信道的频率色散和时间色散,所以短波信道可以表示为二维的频率-时间色散信道,即用散射函数S(τ,fD)来表示.Vogler信道模型是Vogler等[16]根据Wagner等[17]的实验数据推导出信道脉冲响应、传递函数和散射函数而构建的数学模型.
信道的输出信号函数可表示为式(1):
(1)

基于Vogler信道模型的Gaussian型信道散射函数数学模型可表示为:
(2)
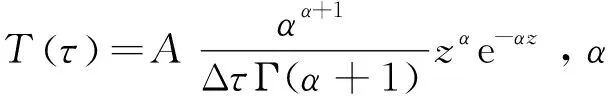
因此利用IRI模型获取电离层电子密度信息后,只需要计算中心频率处的平均时延τc、单边时延展宽τD(τc-τl)、中心频率处的平均多普勒频移fs、单边多普勒展宽σD(暂时无法获得,设为定值0.1 Hz)和接收信号的振幅峰值A后便可建立Vogler模型的短波信道散射函数.其余参数如Afl参考实际接收机参数,α设为1.具体的参数估计算法如下所示.
(1)中心频率处的平均时延τc
数值型三维射线追踪是通过求解微分方程组[18]的方式来求得射线的传播路径,在电离层信息已知的情况下,给定发射点与接收点经纬度、利用Runger-Kutta法求解微分方程组,便可得到射线路径上不同点的坐标矢量和波矢量,将所有点连接起来就可以得到完整的射线描迹,从而得到传播路径的主要参数,如群路径P、大圆距离D等.
那么中心频率处的平均时延τc可由式(3)表示:
(3)
式中:c为真空中的光速;μg为路径上射线的群折射率,为了简化运算,忽略碰撞和外磁场的影响,群折射率μg约为1+40.3Ne/f2,Ne为电离层电子密度,f为电波频率.
(2)单边时延展宽τD
由于信号具有一定的带宽,处于信号带宽内的两个不同频率的短波射线传播路径不同,从而产生了时延差,时延展宽可由式(4)表示:
τD=τc-τl,
(4)
式中,τl为信号带宽频率下限处的平均时延,计算方法参考τc即可.
(3)中心频率处的平均多普勒频移fs
电离层整体的抬高或下降会使接收站接收到的电波频率与发射的电波频率产生一定程度的频移.中心频率处的平均多普勒频移fs可由式(5)表示:
(5)
式中:λ为发射电波波长;P′为电波传播中的相路径.
(4)接收信号的振幅峰值A
对于每一条短波射线,接收点的场强中值由ITU报告中P.533-14中的天波场强计算公式给出:
A=136.6+Pt+Gt+20lgf-Lb,
(6)
式中:A为振幅峰值,单位dB(μv/m);Pt为发射机功率的数值,单位dB(kW);Gt为发射天线增益的数值,单位dB;f为发射频率的数值,单位MHz;Lb为射线路径的基本传输损耗的数值,单位dB,由式(7)给出:
Lb=32.5+20lgf+20lgP+Li+Lm+Lg+Lh+Lz,
(7)
式中:P为射线传播的群路径的数值,单位m;Li为吸收损耗的数值,单位dB;Lm是射线频率高于最高可用频率时的损耗的数值,单位dB;Lg为中间反射点的地面损耗总和,单位dB;Lh是极光和其他信号损耗的因子;Lz为其他损耗的数值,单位dB.
2 基于Vogler信道短波时差测量的克拉美罗界
不考虑多径效应的影响,信号从辐射源(T)经电离层传播后到达接收站(R),时差测量模型如图1所示,本文将短波信道下的时差测量模型描述如下:

图1 时差测量模型图Fig.1 Time difference measurement model
(8)
式中:s(t)表示短波实信号;H1(f,t)和H2(f,t)分别表示两条传播路径中的冲激响应函数;*代表卷积;n1(t)和n2(t)分别表示两条传播路径中的加性噪声,且均为实信号.假设信号s(t)与噪声n1(t),n2(t)不相关,时间延迟为D.x1(t)和x2(t)为经过不同信道调制后加上噪声得到的输出信号.
当多普勒扩展(仿真中设为定值0.1 Hz)不影响信号相关性时,把电离层对短波信号的调制作用简化为短波信号的幅度衰减[19].在这种条件下,经过电离层传播的时差测量模型可简化为式(9)的形式:
(9)
式中,h1和h2表示短波信号经过不同信道的幅度衰减系数,将xi(t)的傅里叶系数(指数形式)表示如下[20]:
(10)
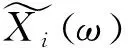
(11)
由平稳随机过程有[21]:
(12)
在平稳随机过程中,Gx1x2(f)代表信号x1和x2的互功率谱密度,且有:
(13)
令
X(k)=[X1(k),X2(k)]T,
(14)
式中:T代表转置,定义功率谱密度矩阵Q使得:
(15)
又因为:
Rx1x2(τ)=E[x1(t)x2(t-τ)]=E{[h1S(t)+n1(t)][h2S(t-(τ-D))+n2(t-τ)]},
(16)
由于信号S(t)与噪声n1(t),n2(t)不相关,经傅里叶变换可得:
Gx1x2(f)=h1h2Gss(f)e-j2πfD,
(17)
同理可得:
(18)
又当τ=D时,互相关运算取得最大值,即时差信息τ包含在功率谱密度函数Gx1x2(f)中,因为Gss(f)为实数,所以有:
(19)
Knapp等指出[11],根据功率谱密度矩阵Q得到克拉美罗界为:
(20)
式中,复相干系数γx1x2(f)定义如下:
(21)
联立式(17)、式(18)和式(21)可知,|γx1x2(f)|2可由式(22)表示:
(22)
式中:Gss(f)为信号的自功率谱密度;Gnn(f)为噪声的自功率谱密度;h1、h2为信号的幅度衰减系数,令Gss(f)=S,Gnn(f)=N,当信噪比(RSN)较小时,则有:
(23)
则,由式(20)可得短波时差测量估计的CRLB为:
(24)
式中:T为积分时间;f2-f1为工作带宽.由式(24)可知,时差估计的标准差为:
(25)
理想状态下,如果短波信号经过电离层没有衰减,即g1=g2=1,则时差估计的CRLB与视距下的CRLB相同.
3 仿真计算
仿真选取的3个观测站分别为:武汉(30.5°N,114.37°E)、道孚(31.0°N,101.12°E)、乐山(29.6°N,103.75°E),其中武汉—乐山地面距离为1 031 km,武汉—道孚地面1 273 km,工作方式为武汉发射,乐山、道孚同步接收,由此得到武汉—乐山和武汉—道孚两条斜测路径,仿真条件为白天发射电波频率10 MHz,夜间发射电波频率4 MHz,信号带宽40 KHz,利用IRI 2016模型模拟冬季白天、夜晚和夏季白天、夜晚不同电离层背景下的Vogler信道散射函数,忽略多径效应影响,只考虑短波信号经过单层传播.
仿真得到的武汉—乐山的高频信道散射函数图如图2所示.

图2 武汉—乐山的高频信道散射函数图:(a)冬季白天;(b)夏季白天;(c)冬季夜晚;(d)夏季夜晚Fig.2 HF channel scattering fuction from Wuhan to Leshan:(a) Winter daytime;(b)Summer daytime;(c)Winter night;(d)Summer night
仿真时间为2020年冬季的1月21日和夏季的7月21日,图2中(a)、(b)、(c)、(d)分别对应着冬季白天(12时)、夏季白天(12时)、冬季夜晚(0时)、夏季夜晚(0时)不同电离层背景下的武汉—乐山短波信道建模,横轴代表多普勒频移,纵轴代表信号的时延,可以看出传播模式均为单层传播.
仿真得到的武汉—道孚的高频信道散射函数图如图3所示:

图3 武汉—道孚的高频信道散射函数图:(a)冬季白天;(b)夏季白天;(c)冬季夜晚;(d)夏季夜晚Fig.3 HF channel scattering fuction from Wuhan to Leshan:(a) Winter daytime;(b) Summer daytime;(c) Winter night;(d) Summer night
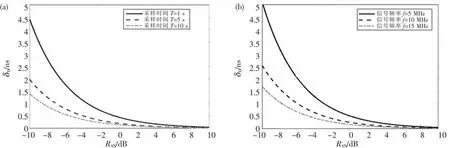
图4 时差测量估计CRLB:(a)不同采样时间;(b)不同信号频率Fig.4 CRLB of time difference measurements:(a) Different sampling time;(b) Different signal frequency
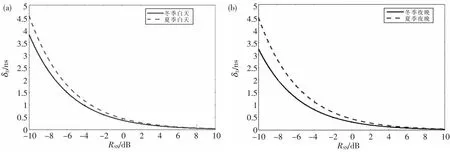
图5 时差测量估计CRLB:(a)冬夏白天;(b)冬夏夜晚Fig.5 CRLB of time difference measurements:(a) Winter and summer daytime;(b) Winter and summer night
图3中(a)、(b)、(c)、(d)分别对应着冬季白天(12时)、夏季白天(12时)、冬季夜晚(0时)、夏季夜晚(0时)不同电离层背景下的武汉—道孚短波信道建模,仿真时间与武汉—乐山短波信道相同,横轴代表多普勒频移,纵轴代表信号的时延,可以看出传播模式也均为单层传播.
根据式(6)可以计算出接收信号的幅度峰值,不同电离层背景下信号的衰减程度不同,导致接收信号的幅度峰值不同,将接收信号幅度峰值与无衰减情况下的理论接收幅度之比定义为幅度衰减系数,当固定电离层对短波信号的影响,将幅度衰减系数设为h1=h2=0.3时,由图(4)可知,短波信号时差估计的CRLB与信号采样时间T,信号频率f,输入信噪比RSN有关,信号采样时间越长、信号频率越大、输入信噪比越高,短波时差测量的CRLB越低,即所得时差精度的最优下界就越高.
将信号采样时间定为3 s,白天工作频率为10 MHz,夜间工作频率为4 MHz,信号带宽为40 KHz,计算冬季3个月(12月、1月、2月)和夏季3个月(6月、7月、8月)的幅度衰减系数均值,代入式(25)中进行仿真,由图(5)可知冬季的短波时差测量CRLB小于夏季,即在冬季所得时差精度的最优下界高于夏季,但随着输入信噪比的增大,季节对时差测量CRLB的影响并不明显.
4 结论
本文以IRI模型和数值型三维射线追踪为基础构建了Vogler短波信道模型,介绍了基于Vogler信道模型提取时延信息的方法并推导了在多普勒扩展不影响信号相关性时的短波时差测量CRLB.仿真了在不同采样时间、不同电波频率、不同输入信噪比、不同季节条件下的时差测量CRLB,结果表明采样时间越长,发射电波频率越大,输入信噪比越高,时差测量误差的标准差越小,所得时差精度越高,冬季的时差测量CRLB小于夏季.当多普勒展宽对短波信号有明显解相关作用时的时差测量CRLB有待进一步研究.

