事件触发机制下基于观测器的连续网络化Markov跳变系统的控制器设计
林凡钧,刘 月,陈惠英,王燕锋,潘 峰,陈林峰
(1.湖州师范学院 工学院, 浙江 湖州 313000; 2.鞍钢集团 本钢北营能源管控中心, 辽宁 本溪 117000; 3.宿迁学院 机电工程学院, 江苏 宿迁 223800; 4.湖州久鼎电子有限公司, 浙江 湖州 313000)
0 引 言
在工业系统中,计算机通信网络和控制越来越集成,将通信网络引入控制系统已成为趋势.由共享网络形成的闭环反馈控制系统称为网络控制系统(Networked Control Systems,简记 NCS).NCS具有系统布线少、成本低、维护与扩展方便等优势[1],目前已被广泛应用于工业自动化领域[2-6].
由于通信网络的引入,不可避免地会发生网络诱导时延、网络拥塞、数据包丢失和数据时序错乱等,这会降低系统的稳定性,甚至严重破坏系统.相对随机发生的网络问题,网络诱导时延是网络固有的问题.周红艳等将系统建模为具有范数有界不确定的离散时间系统,以减小网络诱导时延对其保守性的影响[7].还需考虑的另一个设计约束是NCS的网络带宽有限.控制任务是周期性执行的,但周期性时间触发的通信方案对有限网络资源的利用效率低.Heemels等从系统的分析和设计考虑,使用周期的采样方式[8-9].为进一步减少网络带宽资源的不必要浪费,Tiberi等提出事件触发机制.该方法能够有效克服传统周期采样控制方法的缺点[10].Wang等研究时滞的离散网络控制系统的动态事件触发故障检测问题,提出一种新的动态事件触发方法,并通过构造Lyapunov泛函,推导出闭环网络控制系统的充分稳定性条件[11].
现有关于NCS的研究,大多以线性定常系统为研究对象.而在实际系统中,由于环境、内部子系统连接方式等突然的变化,普通的线性系统已不能准确描述其动态特性,所以混杂系统应运而生.Markov跳变系统(Markov jump systems,简称MJS)作为一类特殊的混杂系统,因具有简单的数学描述形式和强大的建模能力而受到各界的青睐,现已被广泛应用于交通系统、制造系统和电力系统等领域[12-14].MJS是由一个或多个不同的子系统组成的,通过转移速率的变化随机从一个模态切换到另一个模态.熊威等研究一类具有时滞的MJS有限时间控制器设计问题,采用自由权重方法给出MJS有限时间有界性和有限时间H∞有界性的判定准则,从而求出状态观测器和状态反馈控制器的增益矩阵[15].Zhang等提出部分未知转移概率的概念不需要任何未知元素,并研究具有部分未知跃迁概率的连续时间和离散线性MJS的稳定性和镇定问题[16].Zhang等研究具有时变时滞的连续线性MJS的滤波器设计问题[17].彭春源等基于李雅普诺夫泛函方法,研究一类不确定时滞广义半MJS的随机稳定性[18].研究观测器的设计是十分重要的.王国良等研究广义MJS的部分模态依赖观测器及相应控制器的设计问题,对观测器的设计进行了考虑,并设计了一个基于观测器的控制器[19].
现有多数基于事件触发机制的网络化MJS的研究,未考虑通信网络时延的影响,或只考虑单侧时延情况,而以MJS为研究对象同时考虑传感器到控制器和控制器到执行器两段时延的相关研究较少.本文以连续MJS为研究对象,同时考虑双侧时延,提出基于事件触发机制的控制器与观测器协同设计方法.本文的创新点有:
(1)考虑传感器到控制器和控制器到执行器同时存在时延,在控制器端构造观测器,基于观测器的输出反馈控制,对信号传输时序进行分析,将闭环系统建模为具有两个时延的时滞系统.
(2)构造合适的李雅普诺夫泛函,根据李雅普诺夫稳定性理论,得到保证闭环系统随机稳定性的充分条件,并给出控制器与观测器的协同设计方法.
1 问题描述
考虑以下一类具有不确定性的MJS:
(1)
其中,x(t)∈Rn、u(t)∈Rm、y(t)∈Rq分别为系统状态向量、输入向量和输出向量,A(rt)、B(rt)、C(rt)为具有合适维数的实常数矩阵.{rt,t≥0}取值于有限集合≜{1,…,N}的连续的Markov过程,其具有以下模式转移速率:
其中,Δ>0,limΔ→0(o(Δ)/Δ)=0且Πij≥0(i,j∈,j≠i),当j≠i时,Πii=-∑j=1,j≠iΠij,且所有i∈.进一步,Markov过程转移速率矩阵Π定义为:
(2)
注1图1为事件触发机制下基于观测器的网络化MJS结构图.采样器以固定的周期h采集系统的输出信号.采样器采集的信号直接传送给与其相连的事件发生器,事件发生器通过事件触发条件判断接收到的信号是否发送给控制器.下面通过图1说明整个系统的工作原理.
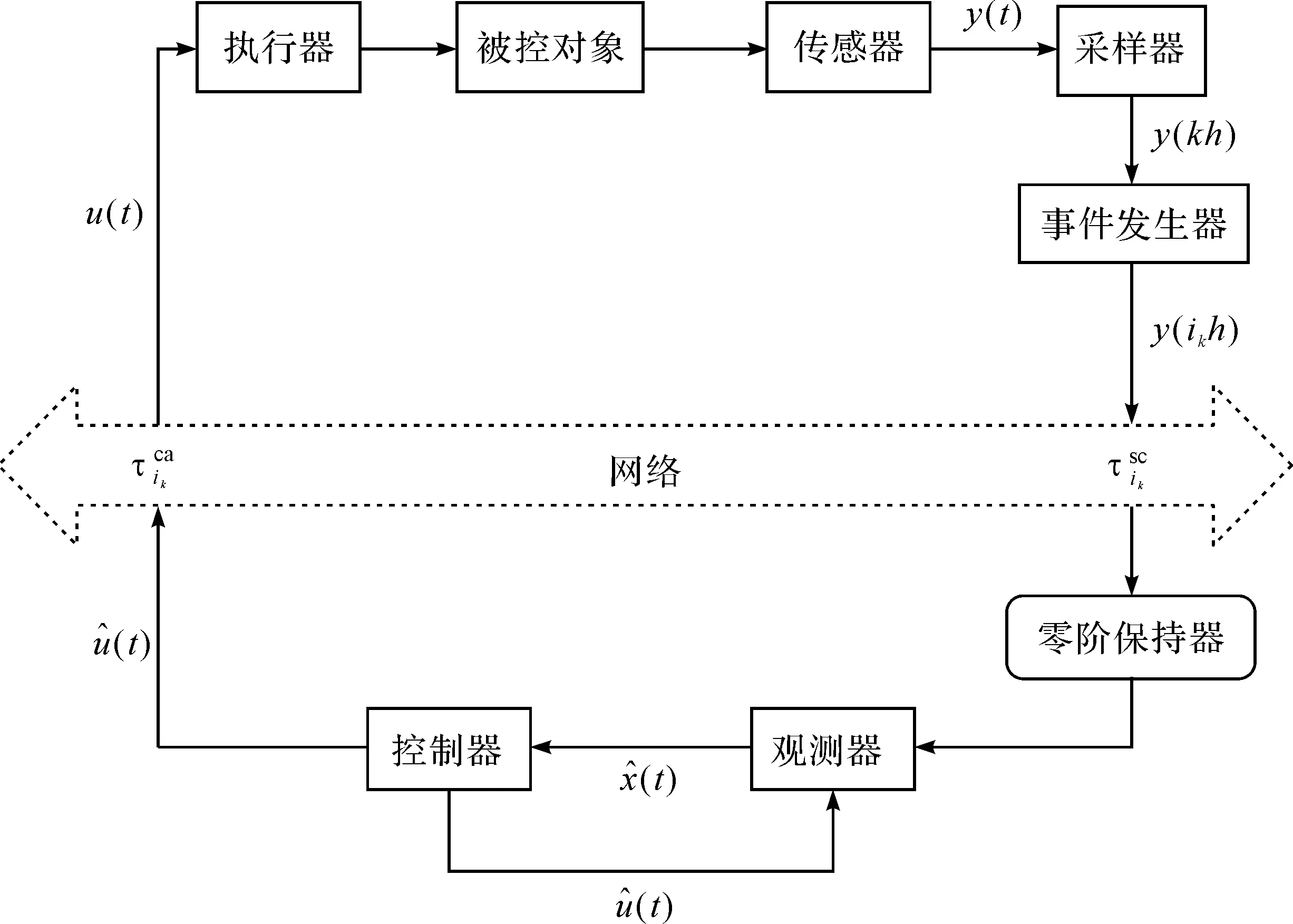
图1 事件触发机制下基于观测器的网络化MJS
首先,采样器以固定的周期h采集系统的输出信号;然后,采样器将采集到的信号直接传送给事件发生器.事件发生器是否将采样数据发送给控制器,需要根据以下条件判断:
[y(ik+mh)-y(ikh)]TV(rt)[y(ik+mh)-y(ikh)]>σyT(ik+mh)V(rt)y(ik+mh),
(3)
其中,y(ikh)为最近一次被传输的数据,y(ik+mh)为当前采样的数据(k=0,1,2,…,m=1,2,3,…),k∈Z+,m∈Z+,V(rt)为正定的事件触发权重矩阵,σ∈[0,1]为事件触发阈值.
注2参数σ、V(rt)、h为通信方案(3)的参数,采集的状态数据y(ik+mh)只有满足二次条件,才会被传送给控制器.显然,通信方案(3)能够降低网络中的通信负载.作为一种特殊情况,若方案(3)中的σ=0,则适用于所有的采样状态数据,方案(3)也将简化为时间触发通信机制.
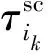
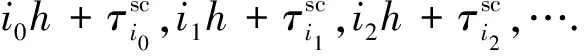
基于上述分析,考虑到通信网络的时延和事件触发通信方案(3)的影响,观测器端收到的系统输出为:
(4)
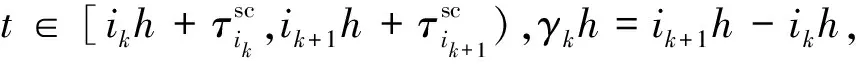
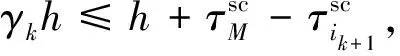
(5)
由式(5)可得:
(6)
定义误差向量为:
∂k(t)=0.
(7)
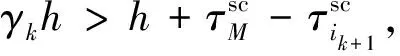
(8)
为便于表达,定义:
(9)
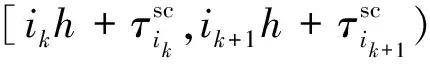
定义函数τ(t)为:
(10)
由式(10)可得:
(11)
定义误差向量为:
(12)

y(ikh)=∂k(t)+y[t-τ(t)],
(13)
(14)
在控制器端构造以下形式的观测器:
(15)
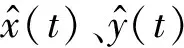
采用以下基于观测器的反馈控制律:
(16)
(17)
其中,K(rt)(∀rt=i∈)为控制器增益矩阵,为便于表达写为Ki.
将式(17)代入式(1),可得:
(18)
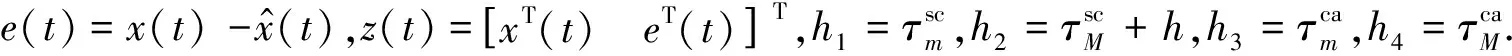
(19)
其中,
定义1[20]若每个初始条件x0∈Rn和r0∈,以下成立,
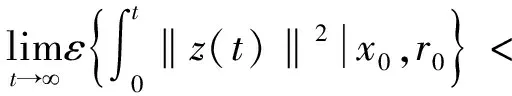
则系统(19)是随机稳定的.
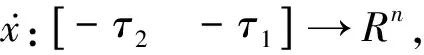
引理2[22]假设f1,f2,…,fN:Rm→R在开集D的子集中有正值,D∈Rm,则在集合D中fi的互反凸组合满足:
2 主要内容
下面给出闭环系统式(19)的随机稳定的充分条件,以及控制器和观测器协同的设计方法.
定理1对给定的标量h1,h2,h3,h4,σ,如果存在合适维数的正定矩阵Pi>0,Vi>0,Rj>0,Qj>0,j=1,2,3,4,以及矩阵Li,Ki,F,G满足下列不等式:
(20)
(21)
其中,
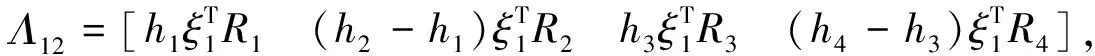
则闭环系统式(19)是随机稳定的.
证明构造以下Lyapunov-Krasovskii泛函:
V(t,z(t))=V1(t,z(t))+V2(t,z(t))+V3(t,z(t)),
(22)
其中,
主人公迎战大鱼时,给大鱼说的话,有蔑视,有“放马过来”的豪情;战胜大鱼后对大鱼说的话充满了胜利的喜悦,同时也有自己的决心和对自己的鼓励。
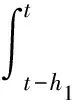
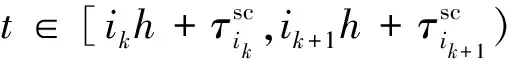
ϑV(t,z(t))=ϑV1(t,z(t))+ϑV2(t,z(t))+ϑV3(t,z(t)).
(23)
其中,
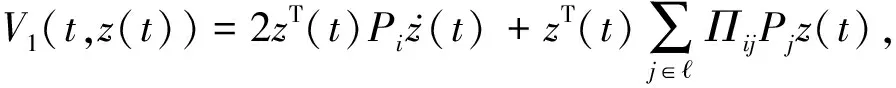
ϑV2(t,z(t))=zT(t)Q1z(t)-zT(t-h1)Q1z(t-h1)+zT(t)Q2z(t)-zT(t-h2)Q2z(t-h2)+zT(t)Q3z(t)-zT(t-h3)Q3z(t-h3)+zT(t)Q4z(t)-zT(t-h4)Q4z(t-h4),
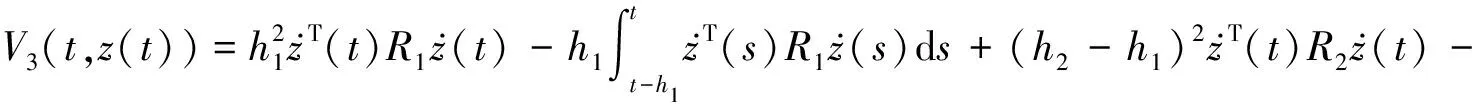
应用引理1和引理2处理式(23)含有的积分项,可得:
(24)
其中,
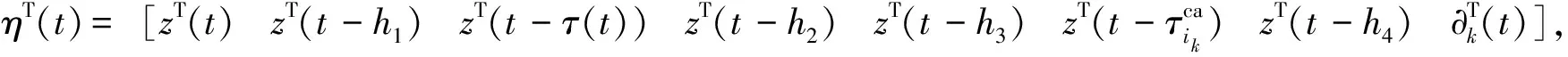
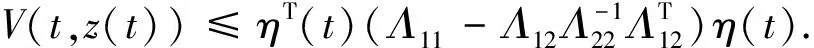
(25)
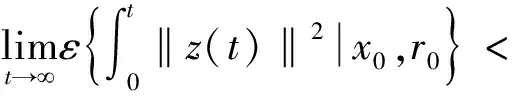
定理1给出了闭环系统式(19)随机稳定性的充要条件,定理2将在定理1的基础上,给出控制器、观测器的增益矩阵,以及事件触发权重矩阵的求解方法.
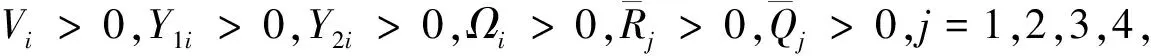
(26)
(27)
其中,
则闭环系统式(19)是随机稳定的,控制器增益矩阵Ki、观测器增益矩阵Li、事件触发权重矩阵Vi可由下式求得:
证明定义
在矩阵式(21)左右两边分别乘以JT和JT,设
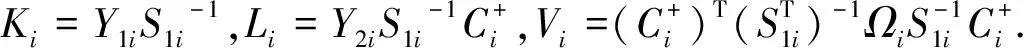
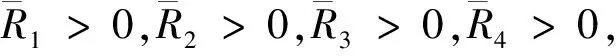
(28)
式(28)等价于
(29)
最后,式(26)通过Schur补引理可得式(20).定理2得证.
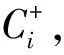
3 仿真算例
下面通过一个例子说明所提结果的有效性.
根据定理2,得到系统正常运行时的控制器增益矩阵Ki、观测器增益矩阵Li和触发矩阵Vi.其结果为:
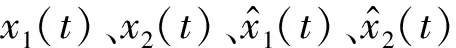
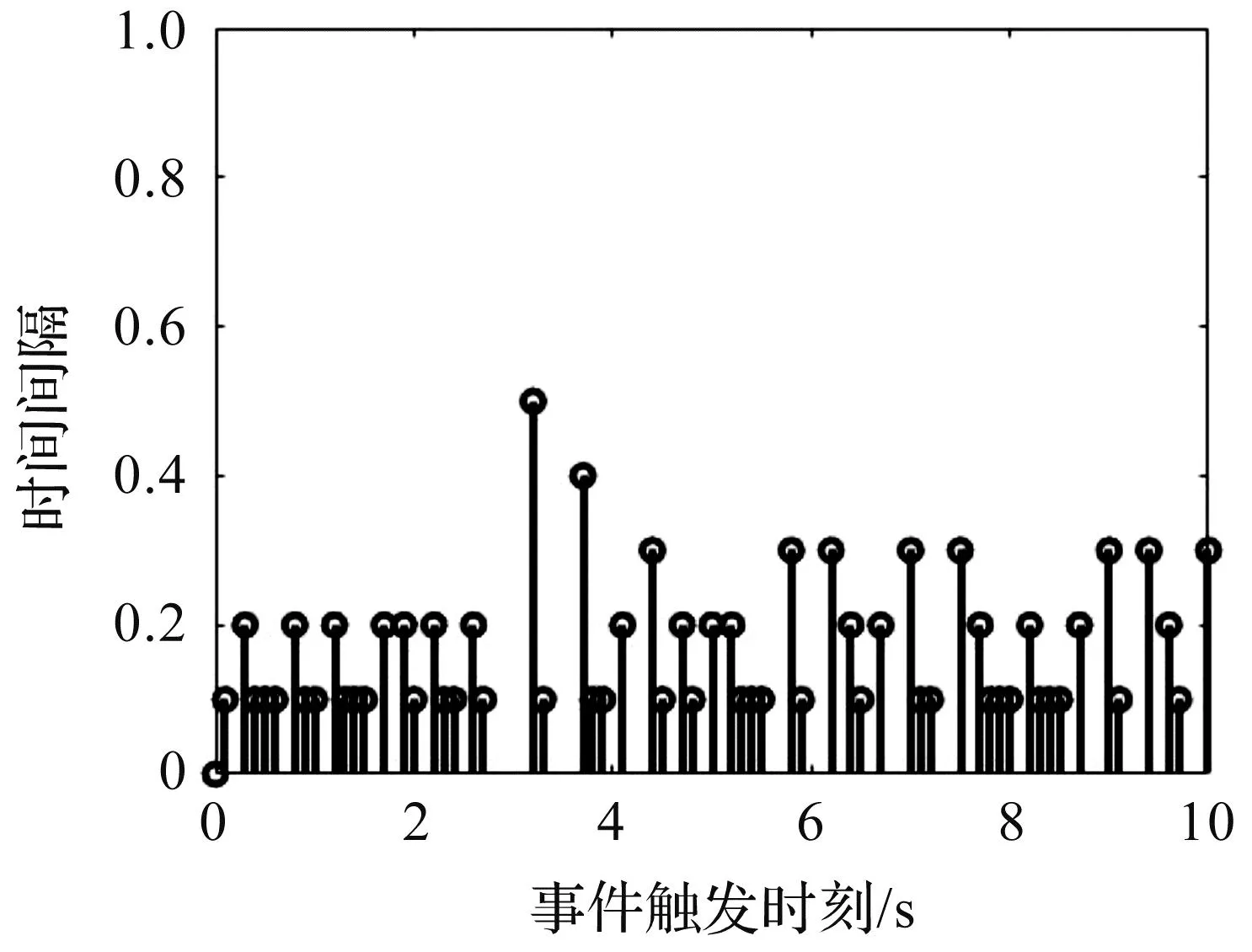
图2 事件触发NCS的传输时刻与时间间隔
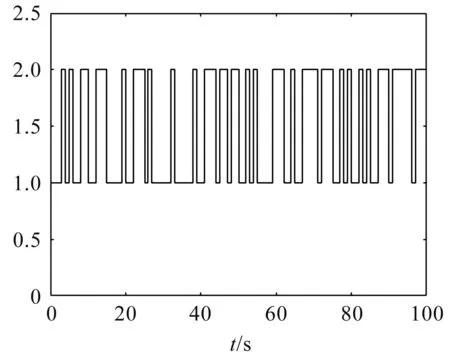
图3 闭环系统模态
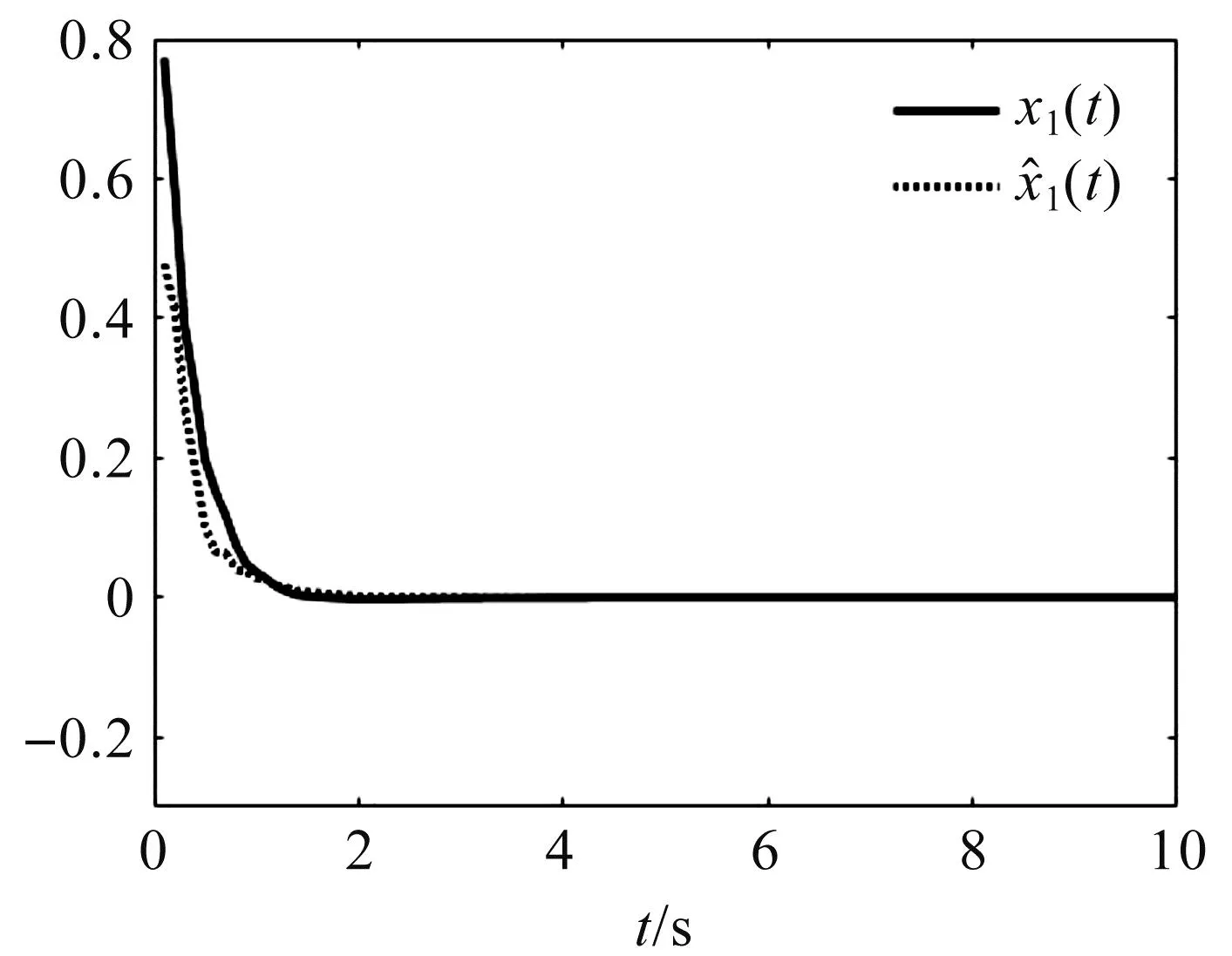
图4 x1(t)及其估计值时的系统状态
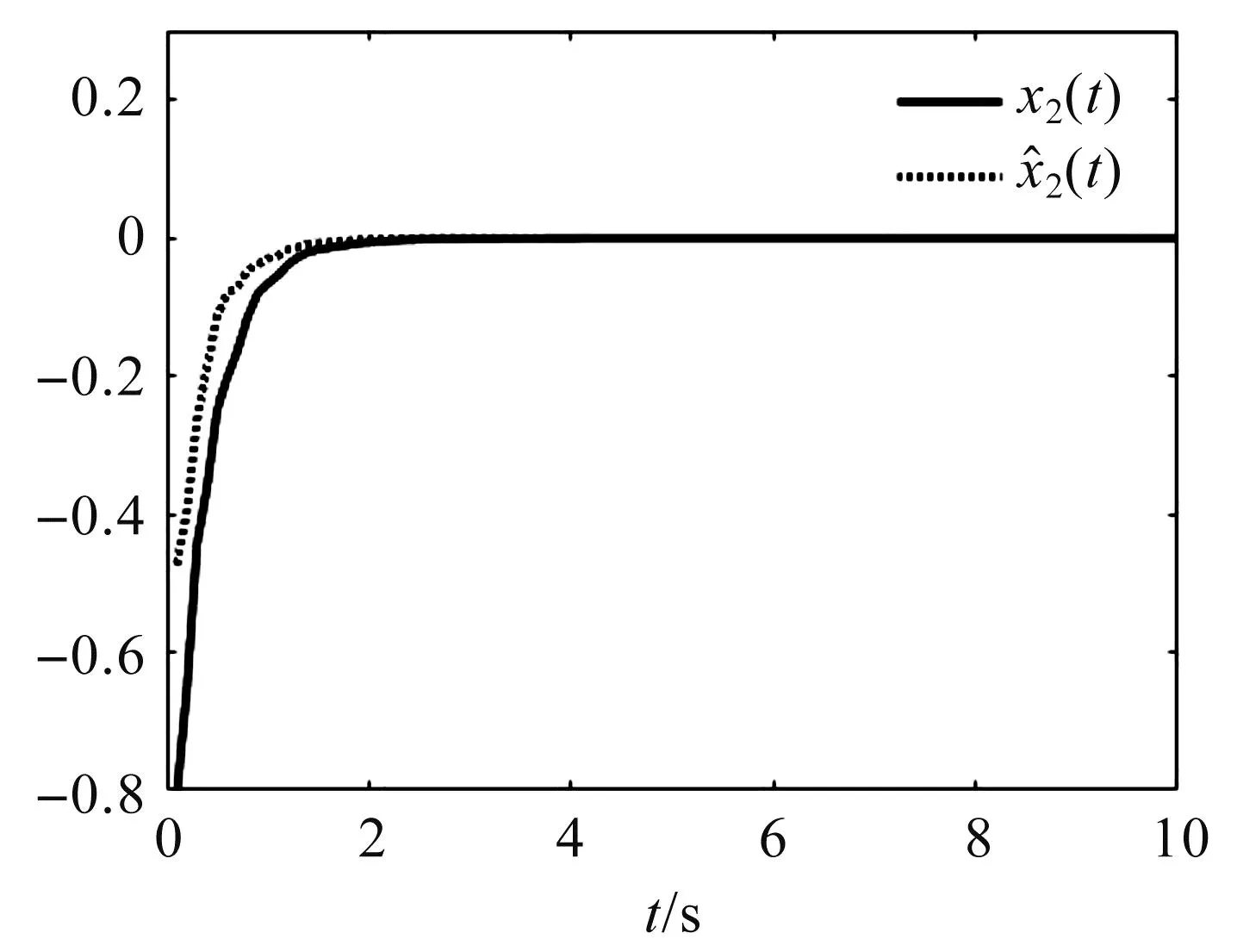
图5 x2(t)及其估计值时的系统状态
由图2可以看出,时间触发通信机制能够节约网络通信资源.由图3和图4可以看出,系统传输的数据在平衡点附近较暂态过程少得多,符合按控制需求传输数据的期望.
4 结 论
本文研究了事件触发机制下基于观测器的连续MJS的控制问题.首先,引入事件触发机制来减少通信负担,采用观测器来获取无法直接测量的被控系统的状态信息;其次,考虑传感器到控制器以及控制器到执行器之间的时延,利用李雅普诺夫稳定性理论和积分不等式,推导建立了保证系统稳定性的充分条件;最后,通过仿真结果验证了该方法的可行性.

