数学文化视角下函数主题的情境教学

⦿ 安徽省临泉第一中学 牛 明

数学承载着思想和文化,通盘渗透“数学文化”是人教版教材非常鲜明的特色.数学文化在人教版教材中主要体现在三个方面:数学史、数学应用、数学思想和方法.本文中基于人教版教材分析数学文化融入函数主题的情境设计.

1 衔接单元:一元二次函数、方程和不等式

文化素材:ag糖水中含有bg糖,若再添加mg糖,生活常识告诉我们糖水会更甜.根据这个生活常识,你能提炼出一个不等式吗?并给出证明.

2 函数

文化素材:(1)对函数概念的再认识(函数起始课);(2)函数概念的形成与发展(数学文化专题).

设计意图：介绍函数概念发展的历程.第一阶段,解析式表示的函数.函数萌芽于17世纪,伽利略对运动学的研究,促进了笛卡儿对动点轨迹的研究.函数是用运动、变化的观点研究客观世界中相互关联的量之间的依赖关系.第二阶段,18世纪伯努利和学生欧拉给出的函数概念.这个阶段的函数概念很接近初中的定义,突出函数是变量的依赖关系和对应关系.概念中有不严谨地方,如“变量x的每一个值”中变量在什么范围内取值?在什么范围内变化?第三阶段,20世纪初美国的维布伦将变量的取值范围看成集合.将函数看成两个集合之间的对应关系,得到高中函数的定义.第四阶段,现代函数的应用已渗透到数学、计算机科学、自然科学乃至人文科学的各个领域中,由于物理学的推动和数学理论发展的需要,函数概念也有了新发展,出现测度函数、广义函数等新的研究分支.

3 幂函数、指数函数、对数函数

3.1 幂函数

文化素材:(1)指数幂概念的推广;(2)幂函数在实际生活中的应用.

设计意图：(1)理解用有理数指数幂逼近无理数指数幂的数学思想方法;(2)教材结合物理知识探究“小水滴掉不下来形成雾的原因”,得到三种正整数次幂函数,又结合“点光源发出强度与距离x的平方成反比”引出负整数次幂函数,引导学生了解数学知识的应用价值.

3.2 指数函数

文化素材:教材例举了大量指数爆炸和指数衰减的现实素材,如C14的指数式衰减用于考古学检测生物体死亡时间,核铀变、GDP是指数式增长模型,等等.

设计意图：激发学习兴趣,让学生感受到数学来源于现实生活,同时又指明研究的对象.引导学生观察现象,发现问题、提出问题,经历分析问题的过程,直至解决问题,让数学成为刻画现实世界运动变化的工具.

3.3 对数函数

文化素材:钴60射线穿过铅板后强度指数式衰减,已知强度比,求铅板厚度;介绍对数发明者纳皮尔;用对数计算地震震级;数学文化专题——历史上的对数.

设计意图：创设问题情境,从实际应用中引出一种新的运算——对数运算;附加式融入数学史,介绍数学家;例题中渗透对数的实际应用;以数学文化专题的形式介绍对数发展史.

3.4 函数与方程

文化素材:方程的根与函数的零点;用二分法求方程的近似解.

设计意图：介绍函数、方程、不等式之间的联系与转化的数学思想;教材中以检修电路创设生活情境,从中抽象出二分法求解方程近似解的数学思想.注重知识的应用背景,让学生体会数学来源于生活,是对现实的高度抽象,体会逼近的数学思想.

3.5 函数模型及其应用

文化素材:(1)几种函数增长快慢的比较.例举大量生活案例(如城市的电话号码升级、合理编排辞典查单词的工作量、互联网搜索),使学生进一步体会“对数增长”“指数爆炸”,并对不同函数增长的差异形成鲜明的认知.(2)数学应用——形形色色的函数模型.(3)习题——函数增长快慢与图象的凹凸性.

设计意图：(1)人教版教材在编写时,在语言上适度口语化,尽量用贴近学生生活和情感的、通俗易懂的语言来讲明数学内容最精华的内核.这节课以函数运动会的形式来表现不同类型函数增长的快慢,这样的呈现新颖活泼、趣味盎然.具体分为四部分,即问题引入、同组比赛、不同组比赛、函数增长速度变化.利用信息技术将图象延伸,展示各函数的走势与整体,就能比较得出结论.借助图象可以比较直观地看出不同函数增长的快慢,但这还不够,还需要从定量的角度展开研究.利用定性与定量相结合的研究方式,感知并理解不同函数的增长差异.(2)数学建模是数学应用的重要形式,教师要鼓励学生从数学的视角发现问题、提出问题、分析问题,进而构建模型、确定参数、计算求解、验证结果、改进模型,最终解决实际问题.学生经历有声有色的数学建模过程,有助于发展问题意识和创新意识,并内化为数学核心素养.(3)习题设计:

向高为H的水瓶中注水,注满为止.如果注水量V和水深h的关系如图1所示,那么水瓶的形状是( ).

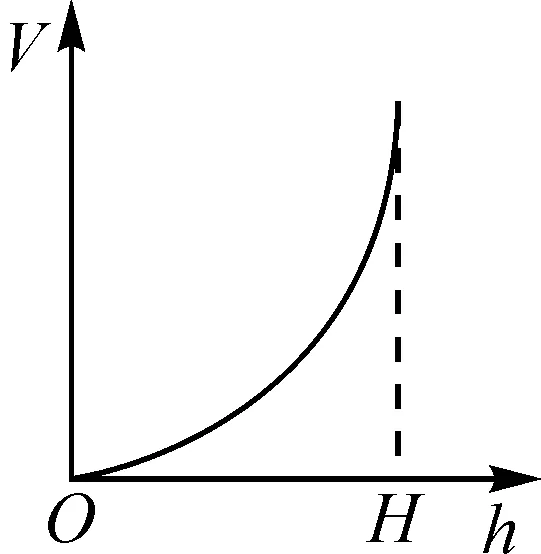
图1

在习题中渗透数学史:琴生(Jensen)不等式.函数“越跑越快”,满足不等式

函数“越跑越慢”满足不等式

4 三角函数

文化素材:(1)弧度制的引入;(2)弧度制和角度制互化;(3)习题——航海上最初规定地球子午圈的1分弧长为1海里,根据此规定计算1海里的长度;(4)正弦型函数y=Asin(ωx+φ)的应用模型,参数A,ω,φ的物理意义.

5 三角函数模型的简单应用

文化素材:(1)例1研究单摆小球离开平衡位置时的位移随时间呈周期性变化的问题;例2以摩天轮为现实背景,经历匀速圆周运动的数学建模过程.(2)数学文化专题——三角学的历史.

设计意图：(1)三角函数的应用问题大致分为三类.第一类是匀速圆周运动问题,如摩天轮、筒车的匀速圆周运动的问题;第二类是简谐振动(单摆、弹簧等)、声波、交变电流等物理学中的周期性现象的刻画;第三类是取材于现实生活的近似周期问题,如潮汐问题等.教材通过两个典型例题,让学生体会圆周运动与三角函数模型之间的内在联系,感受数学建模思想,增强应用意识.(2)渗透三角学数学史.三角学是研究三角函数和解三角形的数学分支.它的发展和天文学、几何学有着不可分割的关系.其发展分为三个时期——早期三角学隶属于天文学,起源于对三角形边角关系的定量考察;后来三角学脱离天文学而独立,成为数学的一个分支,这一时期里编制了大量的三角函数表;第三时期欧拉首先提出三角函数的概念,使三角学从静止地研究解三角形问题,发展到用三角函数去反应运动和变化的过程.三角学进一步演变为研究三角函数的三角学,并成为分析学的一个分支.

每个数学知识发现的过程,一定是数学家醉心发现、探究的过程,源于数学之美对人类的召唤.一线教师要研读教材中数学文化内容,多阅读数学史和数学名著以及数学哲学方面的书籍,提升自身数学文化素养,并将其适当地渗透到教学中.