求导换元破三角,必要探路亦可为
——2023全国甲卷理科第21题解法探究和变式拓展
⦿ 四川省双流中学 李小波 曹军才 洛 嘎
1 试题呈现
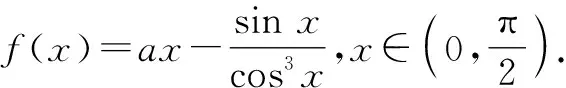
(1)当a=8时,讨论函数f(x)的单调性;
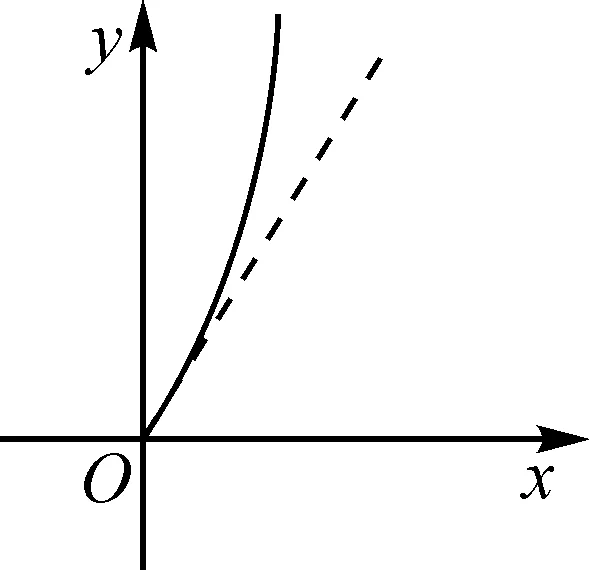
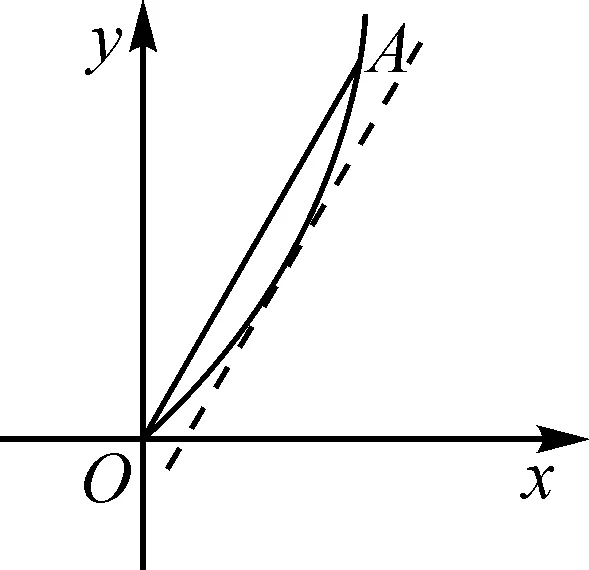
(2)若f(x) 2023年全国高考数学甲卷导数题目,以三角函数为背景,巧妙结合导数和三角函数,通过对导函数的分析,解决函数的单调性、不等式恒成立等问题,深入考查分类讨论、化归与转化思想,考查学生思维的条理性、严谨性.同时,突出素养和能力的考查,考查学生的数学运算、逻辑推理、数学抽象等核心素养,助力创新人才的选拔.下面从三个视角、七种思路对本试题进行解析. 视角一:直接分类讨论. 思路1:分类讨论. 再令h(x)=4x3+2x-6,x∈[0,1],则h(x)在[0,1]上单调递增,于是h(t) 讨论如下: 综上所述,实数a的取值范围是(-∞,3]. 评注:对函数g(x)求导后,为便于分析导函数的正负,通过适当的换元化归为函数S(t),再研究函数S(t)的单调性及取值范围,根据S(t)的取值范围,确定分类讨论的标准,分类讨论即可.此种解法中分类讨论标准的确定自然合理,学生易于理解操作. 视角二:先探必要性. 思路2:必要性探路一——端点效应. 评注:此种方法是观察到g(0)=0,g(x)在原点右侧附近要恒成立,利用端点效应,则函数g(x)在x=0处的瞬时变化率即g′(0)要大于或等于零,得到问题成立的一个必要条件,这样可将实数a的取值范围限定在a≤3,再对充分性进行验证即可. 思路3:必要性探路二——不等式放缩. (ⅰ)当a≤0时,显然成立. 思路4:必要性探路三——重要极限. 视角三:参变分离. 思路5:曲直分离——单调性结合凹凸性分析. 图1 思路6:参变分离之完全分离. 图2 图3 为了充分发挥高考真题在教考衔接中的导向作用,将真题的教学价值最大化,在教学过程中不应只停留在题目的解析上,而更应该对题目进行适当的变式.下面基于此题的结构特点,作一些变式探究与拓展. 近年来,为了有助于创新人才的选拔,高考试题越来越注重对学生核心素养的考查,试题在反套路、反机械刷题上下足了功夫,因此想通过题海战术取得高分的时代已经一去不复返了,这提醒教师在平时的教学中需做好教考衔接.一方面,要关注高考真题,通过真题把握教学方向,充分发挥高考试题的教学价值.另一方面,要努力追求高效课堂,课堂上除了传授知识外,更要以学生为中心,以提高学生的核心素养为目的,培养学生深度思考、自主探究能力,为学生的可持续发展和终身学习奠定基础.2 解法探究
2.1 第(1)问的解法探究
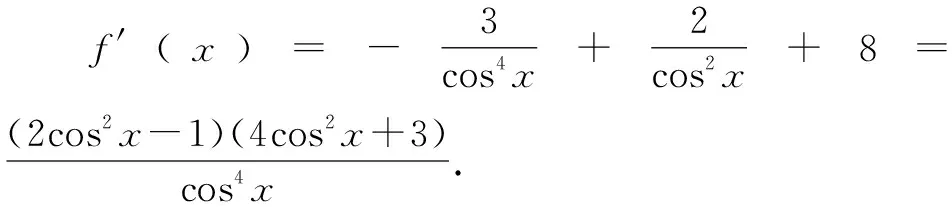
2.2 第(2)问的解法探究
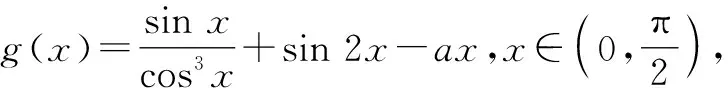



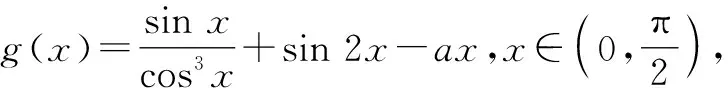






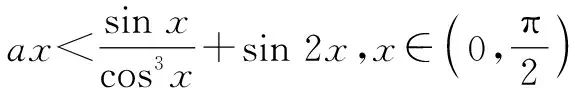

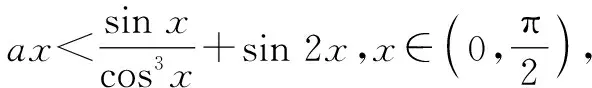


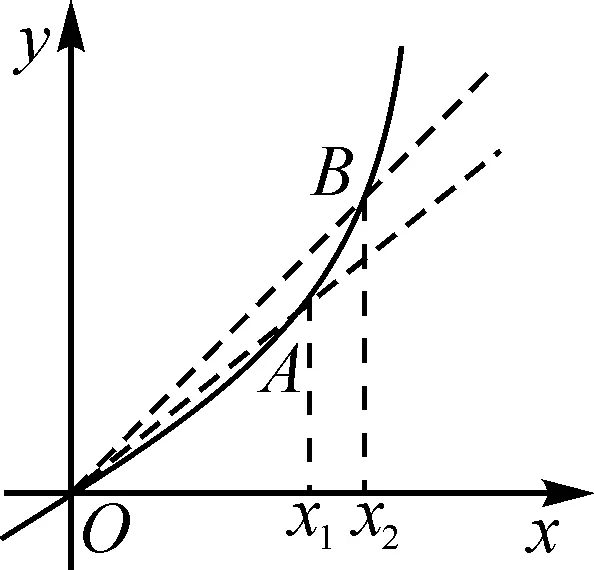

3 变式拓展


4 结语

