基于流固热多场耦合的高速旋转唇形密封性能研究

赵华楠，吕晓仁，吕宝华，项冲，郭飞

(1.沈阳工业大学机械工程学院，辽宁沈阳 110870；2.中航机载系统有限公司，北京 100028； 3.清华大学高端装备界面科学与技术全国重点实验室，北京 100084)

旋转唇形密封(以下简称油封)是一种带有柔性唇的密封部件。由于其结构简单紧凑，加工工艺成熟，摩擦阻力小，因此广泛应用于各种旋转机械用来实现密封并且阻止外界污染物进入。轴旋转时，油封与轴之间的相对转动会产生摩擦，而油封的唇口与轴之间会因泵吸作用而形成一层很薄的润滑油膜，防止润滑油泄漏的同时减少接触区域的摩擦生热。而在航天领域，油封作为动密封常应用在液体火箭发动机中，与普通的旋转机械相比，油封要承受更高的转速和更高的环境温度，摩擦热使唇口温度急剧升高，对油封的密封性能会产生很大的影响。因此，了解油封唇口材料性能变化对油封密封性能的影响具有重要的作用。

从20世纪50年代起，国内外开始关注于油封密封机制的研究。JAGGER[1]通过实验发现油膜的存在，并用电容法测得油膜的厚度，随后提出了张力理论、动压润滑理论等。直到20世纪80年代，钱德森、KAMMULLER、MULLER等[2-4]在大量实验的基础上提出基于密封唇口表面粗糙峰切向变形的反向泵送机制。随着计算机技术的发展，GABELLI和POLL[5-6]用数值仿真来描述表面粗糙峰对接触区流体力学行为的影响，但是没有考虑对油封影响很大的密封唇宏观变形和粗糙峰微观变形。SALANT和FLAHERTY[7]建立了基于反向泵送原理的全膜润滑状态下的弹性流体动力学模型，采用有限体积法对雷诺方程求解，计算油膜压力和切应力，利用影响系数法表示密封唇受力后的变形值，经过迭代计算直到压力和变形均收敛。基于文献[7]的研究，SHI和SALANT[8]采用流固耦合建立了弹流润滑模型，在此基础上GUO等[9]在雷诺方程中引入流量因子，建立了一种基于流量因子的旋转唇形密封的混合润滑模型。JIANG等[10-11]建立了基于确定性表面的混合润滑模型并对油封橡胶进行热老化试验，发现油封在热老化后发生摩擦和磨损行为导致密封件的退化和失效，因此对偶件之间的摩擦热对密封性能的影响不容忽略。赵良举等[12]考虑润滑油膜厚度与黏温效应，分析了旋转轴转速和油封周向载荷对油封唇口温度分布、最高温度和温升的影响，以及唇口温度对油封润滑失效的影响。

现有的数值仿真模型已分析了轴和唇之间产生的摩擦热及润滑介质受温度的影响，但是并未考虑到密封件在高速运动下产生大量摩擦热时会显著提升密封件本身的温度，导致密封材料受热软化，出现径向力减小的情况，从而影响油封的润滑效果和密封性能。

为全面研究油封唇口密封性能随摩擦热的变化情况，本文作者针对处于高转速下的旋转唇形油封，借助ABAQUS软件分析油封唇口接触压力分布受温度的影响，考虑油封唇口润滑油的黏温效应，基于流量因子统计学方法建立旋转轴唇形密封的混合润滑模型，通过对比油封泵送率和摩擦扭矩的理论结果和实验测量结果，验证理论模型的正确性。

1 油封数值仿真模型

文中研究所选取的油封为应用在航空发动机中的带弹簧内包金属骨架型旋转唇形密封，图1给出了其结构示意图。

图1 旋转唇形密封结构示意Fig.1 Schematic of rotary lip seal structure

图2给出了油封密封唇与旋转轴任一周向接触区的示意图。为了方便油封有限元分析和数值模型的建立与分析计算，对模型做出如下的简化与假设：

图2 旋转唇形密封接触区示意Fig.2 Schematic of contact area of rotary lip seal

(1)忽略旋转轴及金属骨架的变形；

(2)忽略旋转轴在启停机时转速变化对动压效应的影响；

(3)密封界面充满润滑介质；

(4)不考虑膜厚方向的压力变化，由于油膜厚度远小于轴的半径，忽略油膜曲率的影响。

1.1 流体力学分析

对于油封接触区润滑油膜的流体力学分析，首先要考虑当油膜压力小于气体饱和蒸汽压时发生的空化现象，因此需引入空化指数F和通用变量Φ来表征空化效应，从而基于流量因子的方法建立二维雷诺方程[9]，如式(1)所示。

(1)

根据PAYVAR和SALANT[13]的空化理论模型，在流体区域

Φ≥0F=1

(2)

在空化区域

Φ<0F=0

(3)

式中：pref为参考压力。

(4)

(5)

(6)

(7)

1.2 接触力学分析

根据混合润滑理论，密封耦合面流体必然存在唇口粗糙峰接触，文中利用Greenwood-Williamson模型(简称G-W模型)模型计算其接触应力，假设所有粗糙峰皆为纯弹性变形，且将粗糙峰间的接触视为半径为R的半球和平面之间的赫兹接触，则接触应力pc和接触面积Ae的计算公式为

(8)

(9)

1.3 变形力学分析

密封唇受过盈及介质压力后唇口会产生变形，由于唇口变形量非常小，符合小变形理论，变形分析可通过影响系数法[14]进行分析来求解密封唇变形量。其油封表面任一节点的法相变形计算公式为

(10)

任一节点的法向变形计算公式为

(11)

1.4 系统温度场分析

旋转轴在高速旋转时，轴与密封件的相对运动会产生摩擦生热现象，在轴运转过程中，一部分热量通过橡胶和旋转轴导热散失到密封件的空气侧和油侧，一部分热量通过轴在旋转时带动润滑介质和空气的流动散失到密封件的空气侧和油侧。摩擦副之间的摩擦热为滑动摩擦产生的热量，有限元分析可得到密封界面宏观接触压力分布情况，通过公式(12)可得到接触区域产生的表面热通量。

(12)

当空气或流体流过固体表面时，会产生对流换热现象。流体带走热量可以用牛顿冷却公式表达：

Q=hq(Ts-Tr)

(13)

式中：对流换热系数hq表征流体与固体表面之间的换热能力，密封系统的各部分所处环境及运动状态不同，对流换热系数需要分别计算。

当旋转轴高速旋转时，与周围流体之间的换热过程为强制对流换热，在旋转方向，轴上各处与周围流体相对速度保持一致，因此可以使用等效外掠平板模型[15]对其换热系数进行计算，即

(14)

式中：Re为雷诺数；Pr为普朗特数，计算公式为

(15)

(16)

式中：v、L分别是线速度、径向流体流动距离；λf、νf、ρf、Cf分别是流体的导热系数、运动黏度、密度、比热容。

在ABAQUS中，在初始固体力学分析的基础上施加计算得到的热载荷，并定义各部件表面的对流换热系数及热传导系数，可计算得到新的唇口温度及接触压力分布情况。

1.5 流-固-热耦合数值分析模型计算流程

图3所示为旋转唇形密封流固热耦合数值仿真分析计算流程，该模型实现了流体力学、接触力学和固体力学之间的相互耦合，这种耦合过程是通过不断迭代，其求解过程通过编写Matlab程序完成。具体流程：

(1)输入油封结构参数以及工况参数，借助ABAQUS对密封系统的影响系数矩阵、接触压力分布进行计算；

(2)输入ABAQUS有限元软件计算得到的计算结果及接触区粗糙峰形貌分布，假设初始润滑脂压力、厚度以及剪切力初值，并输入初始粗糙峰分布；

(3)利用初始膜厚求解二维雷诺方程，直至流体压力满足收敛条件；

(4)对流体力学、粗糙峰接触力学与变形力学三者计算结果根据耦合关系进行迭代求解，调整油膜厚度；

(5)计算唇口表面粗糙峰的切向变形并代入表面形貌分布矩阵中，更新接触区粗糙峰形貌分布，直至粗糙峰的切向变形误差达到收敛标准；

(6)当三层循环的计算结果均实现收敛时，整体数值仿真模型计算完成，随后计算泄漏率和摩擦力矩等性能指标参数。

2 结果分析与讨论

文中所建立的油封模型基本参数如表1所示。

2.1 实验验证

油封的径向力可通过径向力测试仪进行测量，如图4所示，测试轴分为固定半轴和移动半轴两部分，其中固定半轴与测试台刚性连接，移动半轴与力传感器相连。当密封件安装在测试轴上时，移动半轴轻微偏动，触发力传感器，从而测量径向力的大小。所有径向力测试均在室温(25 ℃)环境下进行，每个密封件测量3次取平均值，每次测量过程密封件旋转120°以消除误差影响。

由于弹簧属于非连续体，而在ABAQUS中分析弹簧对密封的影响则需要对弹簧进行特殊处理，将弹簧等效成分布力，在唇形密封安装弹簧的部位施加分布力来模拟弹簧产生径向力的效果。分布力是通过实验测量的结果，利用径向力测试仪测量唇形密封在安装弹簧和不安装弹簧时的径向力，分别用Tr和Tr，elastomer表示(径向力实验中测得)，则弹簧自身产生的径向力为

Tr，spring=Tr-Tr，elastomer

(17)

等效分布力可用下式求得：

(18)

式中：Ds表示弹簧内径；ds表示弹簧横截面直径。

对于名义内径为70 mm的唇形密封，弹簧内径Ds=75.6 mm，弹簧与唇形密封接触的轴向长度ly=2.5 mm。安装弹簧时的径向力Tr=35.14 N，不安装弹簧时的径向力Tr，elastomer=15.95 N，利用式(18)可得等效分布力为pspring=0.032 3 MPa。弹簧的等效分布力可以在有限元中弹簧与油封接触区域施加表面载荷作为有限元分析的弹簧压力输入量，经ABAQUS仿真分析后，将提取到的接触压力分布进行积分换算后得到径向力大小为31.53 N，与径向力测试得到的结果Tr相比误差约为10%。

图4 径向力测试仪Fig.4 Radial force tester：(a) schematic；(b) physical test

如图5所示，为旋转台架实验台结构示意图，通过该台架可以进行油封的正向和反向安装来获取给定工况下摩擦力矩和泄漏率。台架实验中使用的旋转油封直径为70 mm。泄漏的润滑介质由一个集油杯收集，并使用分辨率为0.01 g的精密电子秤进行测量。为了测量摩擦力矩，采用了量程为0～100 N·m，分辨率为0.001 N·m的静态力矩传感器。旋转台架实验在水润滑和室温(25 ℃)条件下进行。

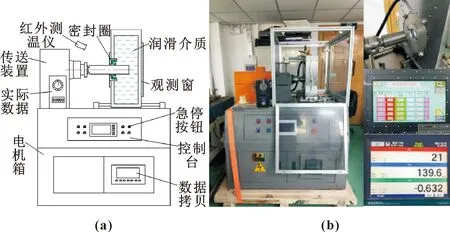
图5 旋转台架实验台示意(a)及实物图(b)Fig.5 Schematic of rotary bench test bed(a) and physical diagram(b)

在0～6 000 r/min转速范围内，以1 000 r/min为间隔调整转速，实验时间为3 h，待达到稳定工作状态后，读取摩擦力矩数值，并通过红外测温仪测试不同转速下唇口温度。图6所示为额定转速下唇口周围温度分布，最高温度位于唇口与旋转轴接触位置，约为59.7 ℃。实验过程中正向安装无泄漏现象发生。图7示出了不同转速下油封的摩擦力矩及油封反向安装的泄漏率，可看出随着转速的增加，摩擦力矩逐渐减小，泄漏率不断增加。

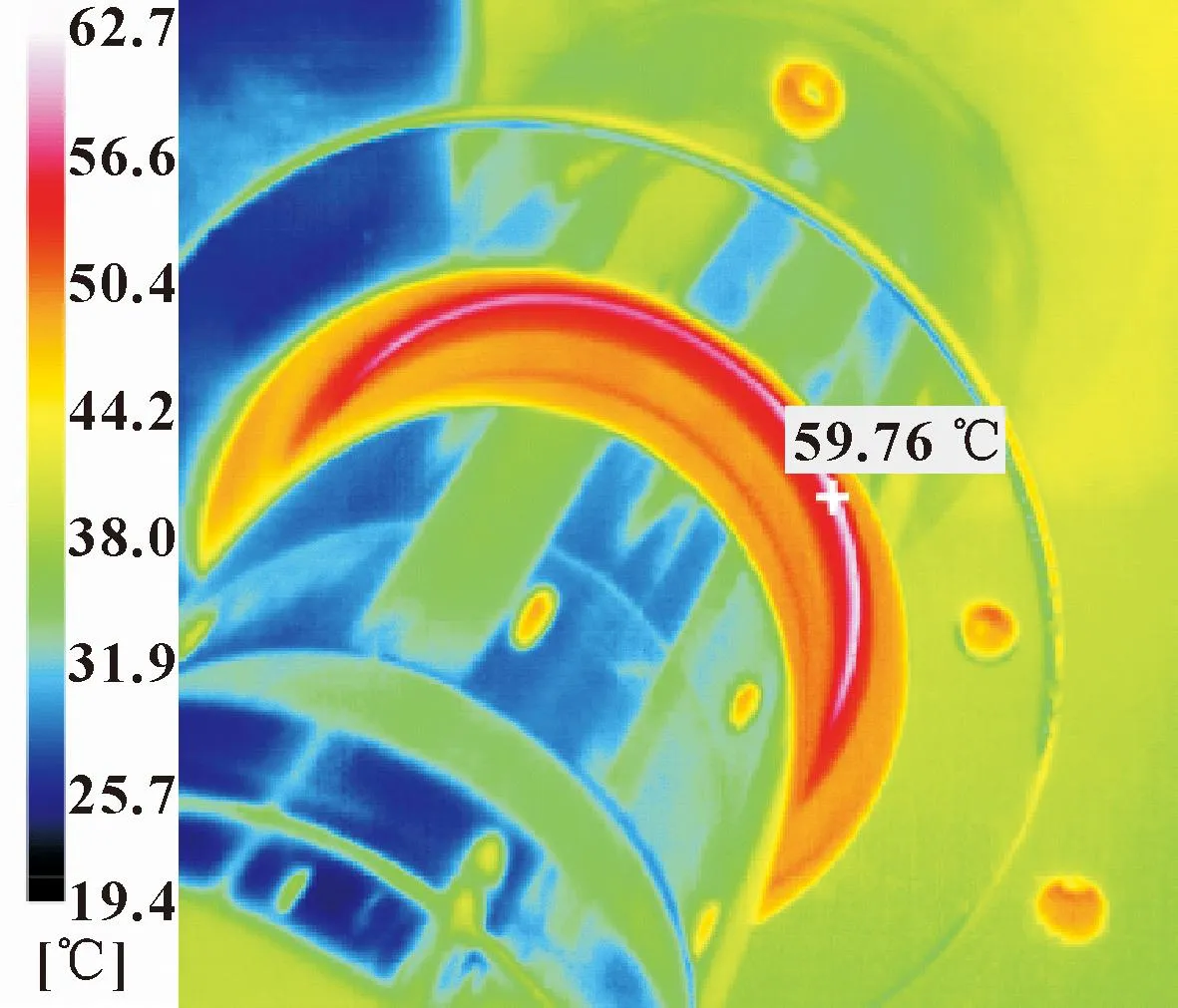
图6 额定转速下唇口周围温度分布Fig.6 Temperature distribution around the lower lip at rated speed

图7 不同转速下油封的摩擦力矩及泄漏率Fig.7 Friction torque and leakage rate of oil seals at different rotational speeds

2.2 数值分析结果

图8—11给出了有限元分析得到的分析结果。图8所示为静态接触与额定转速下密封唇应力分布，可看出相比于忽略摩擦热的情况下，考虑摩擦热时密封唇口Mises应力分布有明显的减小。图9所示为密封唇口忽略摩擦热和考虑摩擦热时的接触压力曲线，其阴影面积表示油封的径向力。可见，忽略摩擦热时最大接触压力为0.87 MPa，接触宽度为0.85 mm，径向力为38.26 N；考虑摩擦热时，油封唇口的最大接触压力为0.69 MPa，接触宽度为1.02 mm，径向力为36.54 N。对比2种情况，影响密封性能的3个重要参数均发生明显变化，由此可见摩擦热对密封唇口接触应力的影响不容忽略。

图8 不同工况下唇口位置Mises应力分布(MPa)Fig.8 Mises stress distribution at lip position(MPa)：(a)in static contact(ignoring friction heat)；(b)at rated speed(considering friction heat)

图9 摩擦热对接触压力分布的影响Fig.9 Influence of friction heat on contact pressure distribution

图10所示为不同转速下密封唇与旋转轴之间的接触压力分布情况。可知，旋转轴转速每增加1 000 r/min，接触压力峰值平均降低0.03 MPa，接触宽度增加0.03 mm。

图11所示为不同转速下油封径向力及唇口温度的变化情况。结合图10中接触压力分布的变化情况可知，随着转速的提高，油封唇口生热明显，由于油液的对流换热系数远高于空气，在油润滑条件下的温升速度相较于在空气中明显降低，不断升高的唇口温度导致唇口处的密封唇材料属性发生变化，密封唇出现软化变形现象，密封唇与旋转轴之间的接触面积也随之变大，并且径向力逐渐减小。

图10 不同转速下接触压力分布情况Fig.10 Contact pressure distribution at different rotational speeds

图11 不同转速下径向力及唇口温度变化Fig.11 Changes of radial force and lip temperature at different rotational speeds

将表1中的参数值以及ABAQUS仿真分析的结果代入混合润滑模型中进行数值仿真计算，得到可定量预测给定工况下密封系统的泄漏率、摩擦力矩等衡量密封性能的关键参数，因实验中油封在额定转速下无泄漏现象，因此文中主要以摩擦力矩为分析对象。

图12示出了不同转速下摩擦热对摩擦力矩的影响，可看出随着转速的增加摩擦力矩逐渐降低，考虑摩擦热后其摩擦力矩的变化趋势更符合实验结果，而在相同转速下考虑唇口摩擦生热现象时，密封系统摩擦力矩却始终低于忽略唇口温升条件时的摩擦力矩，且差值随转速升高而增大，因此唇口接触区产生的摩擦热对油封密封性能具有不可忽视的影响。

图12 不同转速下摩擦热对摩擦力矩的影响Fig.12 Effect of friction heat on friction torque at different rotational speeds

3 结论

基于油封的反向泵送机制，采用统计学方法，建立模拟油封稳态工况下的混合润滑模型，通过有限元分析、数值仿真分析及实验验证的方法，探究唇口接触区域在忽略摩擦热和考虑摩擦热时不同转速下油封的唇口温度分布、接触压力分布及接触宽度的变化情况，主要结论如下：

(1)旋转轴在高速旋转时将产生大量的摩擦热，导致油封唇口处材料软化现象明显，唇口处接触压力下降，接触区宽度增加。

(2)对比考虑摩擦热和忽略摩擦热2种条件下各参数随转速的变化，唇口径向力及摩擦力矩显著降低，密封系统密封性能下降，因此在对高速油封密封性能分析时不可忽略摩擦生热的影响。