蒽醌型染料分子羟基最优取代位置的多目标优化设计方法

颜素崟, 周丽春, 郑 庭, 金福江

(华侨大学 机电及自动化学院, 福建 厦门 361021)

在对染料进行结构设计时,需明确设计目标,即针对染料的溶解度、色谱深度等性能特征进行优化设计。分散染料的不同结构会使染料表现出不同的性能特征[1]。同时,结构改变难以使染料的溶解度与色谱深度等性能都出现正增长,因此,找到不同结构与不同性能特征之间的关系,在这层关系的基础上进行有优化目标的染料分子结构设计,就可更有效率地设计出具有更高性能的染料。文献[2]以C.I.色素红254为原料进行一系列合成实验,得到很多结构不同的新型红色染料,并发现一部分红色染料在存在乙炔键基团的情况下溶解度相对更大;文献[3]以1,4-二氨基-2,3-二羧酸酐蒽醌为原料,与不同碳链长度伯胺进行取代反应制备了多种蓝色染料,发现溶解度会随着碳原子的增多而变小;文献[4]通过合成实验验证了在吲哚的苯环上引入不同的取代基,会对染料的光谱产生影响。然而这种化学实验的研究方法难以确保得到的所有实验结果一定是有效果的。目前在染料分子设计研究中,大多数仍然停留在化学合成实验上。

针对上述设计有效性问题,可通过分子动力学分析不经过实际化学合成就完成对所设计的染料的性能预测,从而提高设计的效率,缩减染料的设计周期。例如:文献[5]使用Materials Studio 软件对丙磺舒固液平衡进行了分子模拟,并发现利用分子模拟计算的丙磺舒与溶剂的相容性顺序与实际人工实验得出的结论一致;文献[6]通过Materials Studio的分子动力学模拟分析了染料在超临界流体中的溶解运动过程,以及染料在超临界 CO2流体中溶解度的微观机制。

此外,分子结构最优化设计方法在相关分子领域取得很多成果。文献[7]阐述了计算机辅助药物分子设计方法,主要是利用分子的三维结构信息进行药物设计。主要设计思路基于受体和所设计分子之间的相互作用信息,又根据活性不同的各种基团实现对分子结构的优化与改造;文献[8]通过构建定量结构-性质关系(QSPR)模型来设计具有不同性质的润滑剂分子,并以经典优化技术求解混合整数非线性规划模型。分子结构设计的定量模型构建完成后,对模型采用相关优化方法进行求解,从而得到最优的分子结构。文献[9]构建了链状苯环结构染料分子的最优化模型,并采用了多目标分层优化算法和差分进化法进行求解,最后得出最佳母体苯环数量和羰基功能团的最优数量。

综上所述,本文通过对染料分子结构更深层次的分析后,分别建立了溶解度和色谱深度与母体分子上的官能团数量和位置的模型,将染料的溶解度作为改善目标,同时确保染料的色谱深度不会低于设计要求,提出的包含分子结构几何特征为筛选规则的隐数法算法进行优化求解,得到最优的染料分子结构。

1 优化模型的构建

1.1 优化模型的初步构建

在染料母体上可以加入的官能团种类众多,如—OH、—NHR、—NH2等。在染料母体确定的情况下,羟基在众多官能团中对染料的多种性能表现最好[10],故本文选用羟基作为进行取代的官能团。

本文选择的染料母体为蒽醌型分子。对已知结构的母体分子,在母体分子上可以插入功能团所有可行位置n可以确定。在染料母体和官能团都已确定的基础上,作为变量的染料结构仅剩下母体上的官能团的数量与位置需要考虑。

图1示出蒽醌型染料母体与取代位置编号。可以看出,在染料母体上对取代位置进行排序,在母体上共有n个取代位置。假设此时共有m个取代位置上存在羟基,则m≤n且m、n都为整数。

图1 蒽醌型染料母体与取代位置编号Fig.1 Number of parent substance and substitution position of anthraquinone dye

为方便模型的构建,可将取代位置的排序图简化成如表1所示的排序表。

表1 母体取代位置排序表Tab.1 Parent substitution location sort table

将取代位置上的羟基存在与否取值为1或0,即存在时取1,否则取0,则一共可以得到2n种取代方案,且这些取代方案表示如下:

X=(x1,x2,……xi),i=1,…,n

式中,xi的值取1或0,表示在染料母体上第i个取代位置上是否插入羟基,因此,加入羟基的数目m与在母体上的位置xi有:

可知,已知羟基加入母体上的位置xi就可以确定羟基的数量m。此时溶解度与色谱深度关于染料结构羟基位置的模型表示为:

y1=f1(X),y2=f2(X)

式中:y1为溶解度的输出值;y2为色谱深度的输出值;f1(X)为溶解度;f2(X)为色谱深度。

文献[9]针对链状苯环结构染料分子的溶解度与颜色进行结构优化设计研究,发现当染料母体的苯环数量变多,分子质量变大时,染料的溶解度会变小,但是色谱深度会变深,即溶解度和色谱深度2个性质是矛盾的。针对此矛盾问题,染料分子结构设计可表示成多目标优化模型如下:

本文根据染料制造对染料设计的实际要求,设计时需要在保证颜色特性的情况下,溶解度越大越好,因此在对色谱深度f2(X)进行限制后,针对溶解度f1(X)进行优化设计。此时就将染料分子设计中染料溶解度与色谱深度2个目标优化问题转化成以染料分子溶解度为优化目标,色谱深度为约束的单目标优化问题。

已知模型中变量取值为0或1,则可知该模型为0-1整数规划问题。结合染料结构几何特征,设计隐数法进行求解。

1.2 染料分子优化模型的构建

1.2.1 溶解度和羟基取代位置之间的模型

1.2.1.1溶解度与内聚能 内聚能表示的是物质聚集时分子间相互作用的强度,是评价分子间作用力大小的物理量[11]。在相同温度、压强、体积和CO2分子数的超临界溶解体系下,染料分子间内聚能越小,染料分子由聚集态转化成单分子态的比率越高,染料溶解的效果越好,溶解度越高。

为找到染料分子间内聚能和溶解度的关系,在Materials Studio的动力学模拟平台上,对CO2-染料系统进行分子动力学模拟,发现在混合体系中,2种物质之间的内聚能之差越大溶解度越大[6]。超临界溶解体系的内聚能之差可表示为

ΔECO2-dye=ECO2-CO2-Edye-dye

式中:ECO2-CO2为溶解体系中超临界CO2分子之间的内聚能;Edye-dye为染料分子之间的内聚能。

当ECO2-CO2为定值时,Edye-dye越小,内聚能之差ΔECO2-dye就越大,因此溶解度最大化问题可转化为染料分子间内聚能最小化问题。具体转变方式如下:

maxRmaxΔECO2-dyeminEdye-dye

式中:R为溶解度;max为取最大值;min为取最小值。

1.2.1.2内聚能与羟基数目和取代位置的模型 在染料母体上不同位置进行羟基取代,会对内聚能E带来不同程度的大小变化。设ci表示染料母体上不同位置进行羟基取代时对内聚能带来的影响大小,且该影响汇总后需要使原母体的内聚能变小,则可得到:

1.2.2 色谱深度和羟基取代位置之间的模型

1.2.2.1色谱深度和最大吸收波长 不同的染料分子结构其光谱曲线吸光强度的大小ε和对应的吸收波长λmax不同。当羟基在染料母体上不同位置进行取代时,得到的同分异构体所计算出的吸收峰的位置在可见光区域内存在些微差异,虽不影响染料的颜色判断,但是紫外吸光强度却因为电子跃迁强度的差异产生了较大变化,吸收波长对应的吸光强度存在明显差异。为得到色谱深度更深的染料,可在母体分子不同的位置上加入不同性能和数量的官能团得到深色谱染料。

1.2.2.2最大吸收光谱与羟基取代位置的模型 设aij表示染料母体上不同位置进行羟基取代时对吸收强度的影响大小,则可得到:

式中:Δε(X)为光谱曲线吸光强度的变化量;aij为取代位置对吸收强度的影响大小;xi为染料母体上的取代位置。

文献[12]提出ε=103～104为中强度吸收,ε=104～105为强吸收。在染料母体不同位置上进行i个羟基取代带来的吸收强度大小变化需大于bi,才能使ε达到一定强度且满足实际情况,则可得约束模型:

Δε(X)≥bi

1.2.3 变量约束

决策变量是0-1变量,则:

1.2.4 构建优化模型

将上述所构建模型组合,即可得到本文所需分子结构优化的0-1规划模型。

2 模型的优化方法与求解

文献[6]提出了以插入的官能团数量n来分组考虑所有的取代方案,并分别用线性规划的方法求出加入不同数量官能团时的局部最佳位置,最终从n个局部最佳位置中确定出全局最优官能团位置的组合优化设计方法。该方法需要完成n个线性规划求解,在母体分子苯环数多,可加入位置n很大时,路径数量会呈指数增长,求解计算复杂性增加。本文在求解关于染料内聚能最小的0-1规划问题时采用对称性隐数法,直接进行全局最优计算。其中隐数法是将求解优化问题转化成在树状图中寻找最优路径的一种优化方法[13]。

2.1 染料分子几何对称结构筛选准则

蒽醌型染料母体分子的几何形状是具有显著对称特征的平面[14]。如图2所示,在母体分子平面上可以找到过分子中心的水平线σx和竖直线σy的对称轴,以对称轴进行反射变换,可以得到取代位置在母体分子上的对称位置[15-16]。如图2中(7)和(6);(7)和(2);(7,8)和(6,5);(7,8)和(1,2),以及(7,8,1,2)和(6,5,4,3);(5,6,7,8)和(4,3,2,1)。

图2 蒽醌分子取代位置排序图Fig.2 Molecular substitution position sequencing of anthraquinone

这些具有完全对称性的位置上加入相同官能团其结构也是相同的,多个分子间的相互作用力效果也是相同的,即在对称位置进行取代,分子间的内聚能相同[17-19],因此,对于具有对称性的位置,只需求出其中一个位置的内聚能,其它对称位置内聚能都相等。这样,找到母体分子可插入点的对称点,就可以减少其相应对称点的优化计算,在0-1规划中排除其对称点的路径,简化优化路径树状结构,提高优化效率。

母体分子平面的对折变换是母体分子平面沿对称轴对折,即将对称轴分离的2个呈180°的半平面绕对称轴旋转成0°的2个半平面,对折后的2个半平面完全重合的顶点(可加入位置)即为对称点。

排除分子平面可加入官能团位置中所有对称位置,通过对折变换,可以找到一个平面的所有对称点、对称线段、对称平面,从而减少分子母体可插入位置的数量,降低计算复杂性。

2.2 对称性隐数法

传统隐数法是沿各路径从左到右依次探测各子问题,直至给出最优解或得出原问题无可行解的结论,过程中需要考虑所有的优化路径。然而对称性隐数法在进行优化计算前先排除对称元素,去除了重复的优化路径,减少了优化路径的探测数量[20]。

综合考虑对称程度的筛选以及隐数法中两层隐数对解集的筛选,设k表示正在探索的解集与可行解目标函数之间的差值,在探索过程中应确保k值不断变小且满足k<0。除要求目标函数减小之外,代表约束函数满足情况的s也应满足s≥0。则隐数法的具体可行解筛选规则如下:

式中:σ0为正在探索的解集;f0为可行解目标函数值;A为m×n维矩阵;b为m维列向量;c为n维行向量;cj为行向量c的第j个值。

求解过程是最优解在k和s的解集筛选中不断更新的过程,直至两层隐数筛选出的解集为{φ}时,最后得到的最优解即全局最优解。

2.3 对称性隐数法的最优条件

进行优化计算时,需要知道进行到什么程度时得到最优解,即达到最优解的条件。

结合上述优化计算过程,可用下式表示处于下降趋势的目标函数:

f=f0-[w(-k)si]

式中:w为不定常数用来确保等式成立;f表示基本可行解;f0表示可行解目标函数值;k表示正在探索的解集与可行解目标函数之间的差值;si表示约束函数。

1)后续当k≥0时,此时现行的基本可行解就是最优解。

2)k<0且si<0时,目标函数持续下降但是由于约束函数s的值不满足,则无新的可行解。由于变量为1或0,约束函数是否满足的变化主要是由约束函数系数确定的,若探测系数满足si+aj′≥0,则目标函数持续下降f→-∞,此时问题属于无界情形。

3)k<0且si≥0时,此时可求出新的基本可行解。

3 实例分析

3.1 蒽醌型染料分子结构优化设计

为证实该优化设计方法的有效性,选择实例验证对象为5,7,12,14-并五苯四酮分子,结构如图3所示。

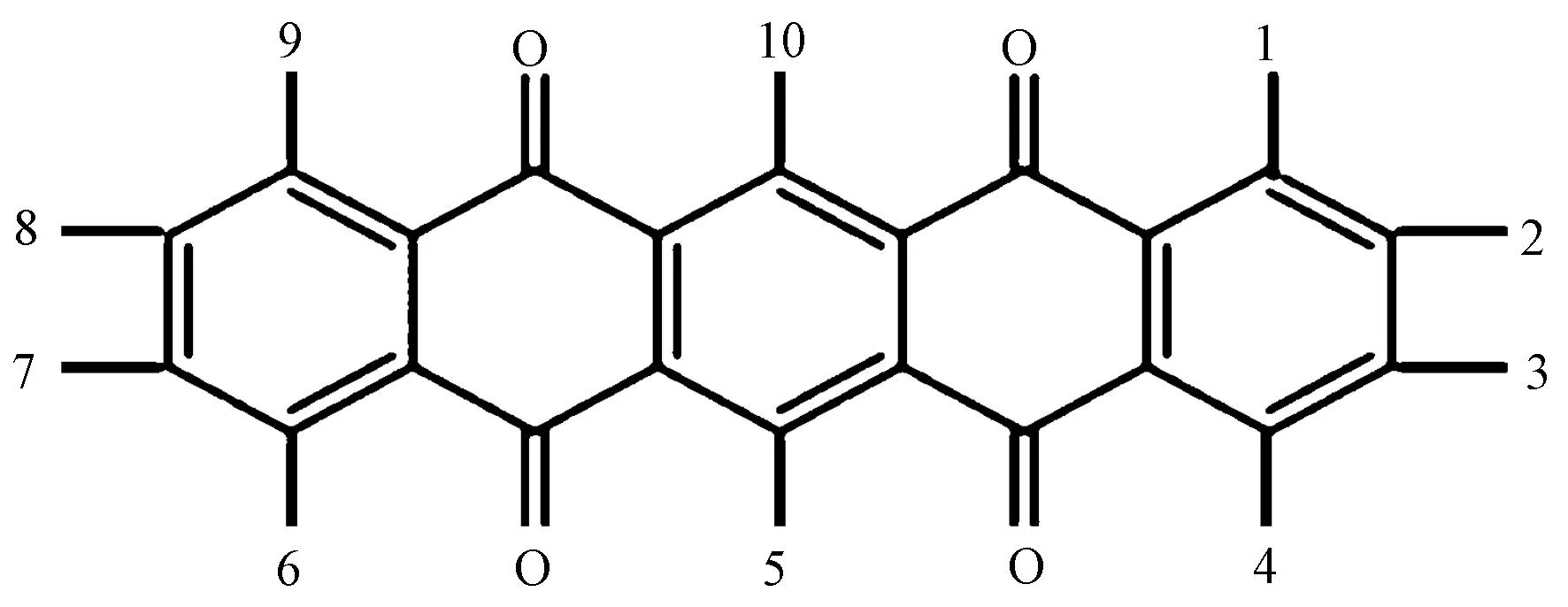
图3 实例验证分子结构与取代位置编号Fig.3 Example validation of molecular structure and substitution position number

羟基在母体上的取代位置共有10个。按上述优化流程可将取代位置简化成表1所示排序表,按取代位置可得到10个0-1变量。

如前文几何对称结构筛选的内容,将该分子结构同样沿着对称轴进行对折变换,可知(1,2)和(4,3)、(9,8);(6,7)和(4,3)(9,8);(1,2,3,4)和(9,8,7,6)以及(5)(10)取代位置可以进行变换。进行后续最优路径求解时,此时已去除部分重复路径。

根据实际染料母体进行优化时,需要确定优化模型中各参数的值。在仅有1个羟基取代的情况下,可看出不同结构的分子和内聚能及色谱深度之间的变化,其中色谱深度用Gaussian软件进行计算,内聚能用Materials Studio计算,不同羟基数目的计算方法相同,具体的计算结果见表2。且该分子母体的原始内聚能为6.371 J和原始色谱深度为10 411.988。按1个羟基取代带来200色谱深度的提高为标准,依次累加,则bi=200i。

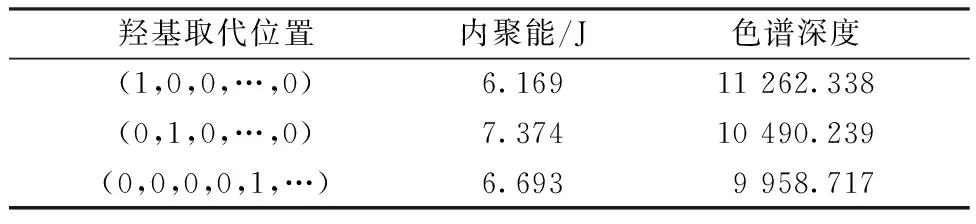
表2 不同取代位置所对应的内聚能以及色谱深度Tab.2 cohesive energy and chromatographic depth corresponding to different substitution positions

根据所求得的内聚能和色谱深度值与羟基取代位置之间的关系,具体优化数学模型求解如下。

先锁定初始可行解:

f0=CX0=-0.202

X0=(1,0,0,0,0,0,0,0,0,0)T

式中:f0为可行解目标函数值;X0为初始取代位置的集合;C为1×10维矩阵。

参考上述存在更优解的条件,在i=2的情况下,满足k<0的J中元素需包含J={(1,4);(1,6);(1,9);(4,6);(4,9);(6,9)},根据几何对称结构的对折原理,又可将后3个元素去除,得到J= {(1,4);(1,6);(1,9)}。此时考虑约束的满足情况,得出s(1,4)、s(1,6)、s(1,9)≥0,则更新可行解为:

f0=CX0=-0.606X0=(1,0,0,1,0,1,0,0,0,0)T

当i=4时,满足k<0得到的J={(1,4,6,9)},但所得s不满足最优解条件。

后续所有可行路径都不满足条件,则现行的基本可行解就是最优解:

f0=CX0=-0.606X0=(1,0,0,1,0,1,0,0,0,0)T

则所设计出的最优分子结构的内聚能为5.765,解集为

X0=(1,0,0,1,0,1,0,0,0,0)T

羟基的取代位置在1,4,6上时,得到最优分子结构。取代后的分子结构如图4所示。

图4 最优染料分子结构Fig.4 Optimal dye molecular structure

3.2 对比验证

经过Gaussian对紫外光谱的计算,设计过程中染料的最大吸收波长的变化不大,但是吸光强度不断变大,结果如图5所示。设计的2种染料之间最大吸收波长差距Δλmax=4.52,仍在相同颜色波段内,但1、4、6位置取代的染料的吸光强度要高于羟基插入其他位置的染料。可见染料的设计过程中色谱深度满足条件。

图5 染料结构可见光波段紫外光谱图Fig.5 Visible-UV spectra of dye structure

为证明设计方法的有效性,将设计出的最优染料分子结构与性质最佳的相似结构染料分子进行溶解性质对比。参考分散染料手册,找出一种已实际生产的分散染料分散紫26的,具体结构见图6。

图6 分散紫26Fig.6 Disperse Violet 26

在Materials Studio分子动力学模拟平台上对设计出的染料分子结构和分散紫26进行溶解过程模拟实验,即构建一个将温度和压强限制在超临界状态且存在二氧化碳分子和染料分子的盒子,然后对其进行分子动力学模拟。

分散紫26的内聚能之差为1.29,但是所设计的最优染料的内聚能之差为1.71,经过二者该值之间的比较可以知道,所设计的染料相较于分散紫26的内聚能之差要更大,溶解性能要更好。

4 结 论

本文提出了一种多目标优化设计方法,解决了染料分子设计中染料溶解度与色谱深度2个指标的矛盾问题。针对实验周期和成本问题,本文使用最优化设计优化母体苯环上的可插入位置,提出的方法针对具有对称性的母体分子,排除对称位置,减少可插入位置数,降低优化计算复杂性。此外,本文还采用了隐数法一次计算出最优加入位置和加入相同功能团的数量,相对组合优化,优化求解效率显著提高。

本文方法仍然存在以下问题待解决:1)仅仅用平面对称性发现对称点,消除可加入冗余位置,但是蒽醌型染料分子平面结构对称性与多个分子间相互作用力、分子平面运动状态演变、内聚能和溶解度有直接关系,建立对称性与分子平面运动状态演变、内聚能和溶解度的模型可从分子几何图形结构设计最优性能的染料,提高设计的效率和准确性。2)最优分子结构的结论是在分子动力学平台上实验验证的,与实际染料分子的溶解度和色谱数据有一定差异。需要用最优分子结构为目标分子结构,合成和制造最优分子结构的染料,并进行染色实验验证染料的溶解度和色谱效果。