移动机械臂牵引卷装纱线的动态建模与控制

许高平, 孙以泽

(东华大学 机械工程学院, 上海 201620)

随着机器人技术与纺织工业智能化的不断发展,利用工业机器人替代人工完成各类典型的纺织加工技能作业已成为纺织行业的新趋势,比如纺纱领域的物料转运机器人、细纱自动落纱机器人、纱线整理打包入库机器人[1];织造领域的筒子架换运机器人[2]、经轴上落机器人[3];编织领域的芯模牵引机器人[4]。以上机器人应用多为固定点位间的搬运或对刚性物体的抓取、牵引等,而将刚性的工业机器人适配于纺织柔性体加工制造,完成技能性更强的拟人化作业仍存在挑战。

在织造整经工艺中,卷装纱线作为织材投入织造加工前,从大量的卷装表面理出线头并牵引至固定点位便是一项技能性要求极高的工作,目前纺织工厂均采用人工操作,该操作过程繁琐费时,人工成本高,生产效率低,且操作工直接接触导致卷装被污染的风险较大。因此,本文在利用自动找线头装置[5]的基础上,采用机械臂对纱架上的卷装预留线头进行抓取与牵引,通过提出一种集成移动机械臂运动规划策略的卷装纱线牵引操纵框架,绕开环境障碍的同时防止纱线被过度拉伸,实现卷装纱头的自动化梳理。

纱线属于可变形线性体(DLOs),当前对DLOs的研究主要有2个方向:高效精确的形状建模和稳健通用的操纵规划[6]。DLOs的动态建模是机器人对其精确控制的基础,目前针对DLOs的建模主要采用质量弹簧模型[7]、多体模型[8]、动态样条模型[9]、有限元模型[10]、离散弹性杆模型[11]与绝对节点坐标方法 (ANCF)[12]等。其中,基于柔性离散体的ANCF能够准确描述大变形体的动力学特性,因此被广泛应用于绳索[13]、电缆[14]、纱线[15]等大变形柔性线形体的动力学建模。机器人对DLOs操纵控制的研究主要有机器人操纵绳子打结/解结[16]、机器人对DLOs形态的控制[17]、机器人操纵DLOs插入孔隙[18]、机器人布线[6]等。相比于其它类型的DLOs,纱线更加细长柔软,机器人与单根纱线间的交互感知困难,因此机械臂对卷装纱线的精确控制更具挑战。

此外,纺织工厂环境往往比较复杂,设备紧凑,机器人运动空间局限,因此机器人牵引纱线运动路径的避障规划也是其成功应用的关键。机器人避障路径搜索的代表性算法主要有概率路标法(PRM)[19]、A*算法[20]、人工势能法[21]与快速扩散随机树法(RRT)算法[22]等。其中,RRT算法因其快速扩散性与概率完整性等优点被广泛应用,但基本RRT存在着随机性强、导向性差、耗时长、冗余结点多、寻迹平滑度差等不足。对此,一些研究者在其基础上做了很多改进[23-25],其中,Xu等[26]提出了自适应引导快速扩散随机树(AGG-RRT)算法,其在路径搜索过程中根据环境中障碍物的分布情况自适应调整偏置目标因子大小,同时兼顾了导向性与全局随机性,搜索时间短,成功率高,已成功应用于复杂织造环境下机械臂的无碰撞轨迹规划。

1 卷装纱线牵引动力学

移动机械臂对纱线牵引操纵的控制框架如图1所示,其中,纱线的动力学建模是实现机器人对纱线精确控制的基础。

图1 移动机械臂对卷装纱线的牵引操纵控制框架Fig.1 Control framework for yarn hauling by mobile manipulator

1.1 卷装表面纱线的数学描述

卷装表面纱线的数学描述示意图见图2。卷装基坐标系位于卷装大端底面中心,其基坐标为{ex,ey,ez}。s为沿纱线弧长的拉格朗日坐标,纱线末端Pe为它的原点,r(s,t)为t时刻纱线上某一点的位置向量。为简化纱线初始状态方程的计算,建立圆柱坐标系,其基坐标为{er,eθ,ez},圆柱坐标系内任意点都可用(r,θ,z)唯一描述,因此P点的坐标向量在圆柱坐标系下可表示为

图2 卷装表面纱线的数学描述示意图Fig.2 Schematic diagram of mathematical description for yarn on package surface

r(s,t)=r(s,t)er(θ(s,t),t)+z(s,t)ez

圆柱坐标系与卷装基坐标系的转换关系为

根据卷装的络筒原理求解卷装表面纱线的初始状态方程。令研究的纱线段在卷装表面从Ps点缠绕到Pe点,纱线段弧长为L;Pe在圆柱坐标系下的坐标为(r0e(θ0),z0ez);V为络筒时纱线相对卷装的卷绕绝对速度。则纱线段上的任一点P的初始状态方程为

式中:β为卷装的锥角;φ为卷装纱线的缠绕角;T为从P点开始卷绕的时长;0≤s≤L。

1.2 运动纱线单元的ANCF模型

对于长径比和大柔性的纱线来说,其截面变形不是关注的重点,从而可忽略沿截面方向的斜率矢量,因此采用ANCF的梯度缺省索梁单元建立纱线动力学模型,以求解纱线被牵引脱离卷装表面的运动控制方程。

如图3所示,梯度缺省ANCF索梁单元的节点坐标由节点位置r及其对轴向物质坐标(0≤≤)的导数r组成。对于P(si)与P(si+1)两点间的第i(i=1,2,…,N)个纱线单元,其广义节点坐标可表示为

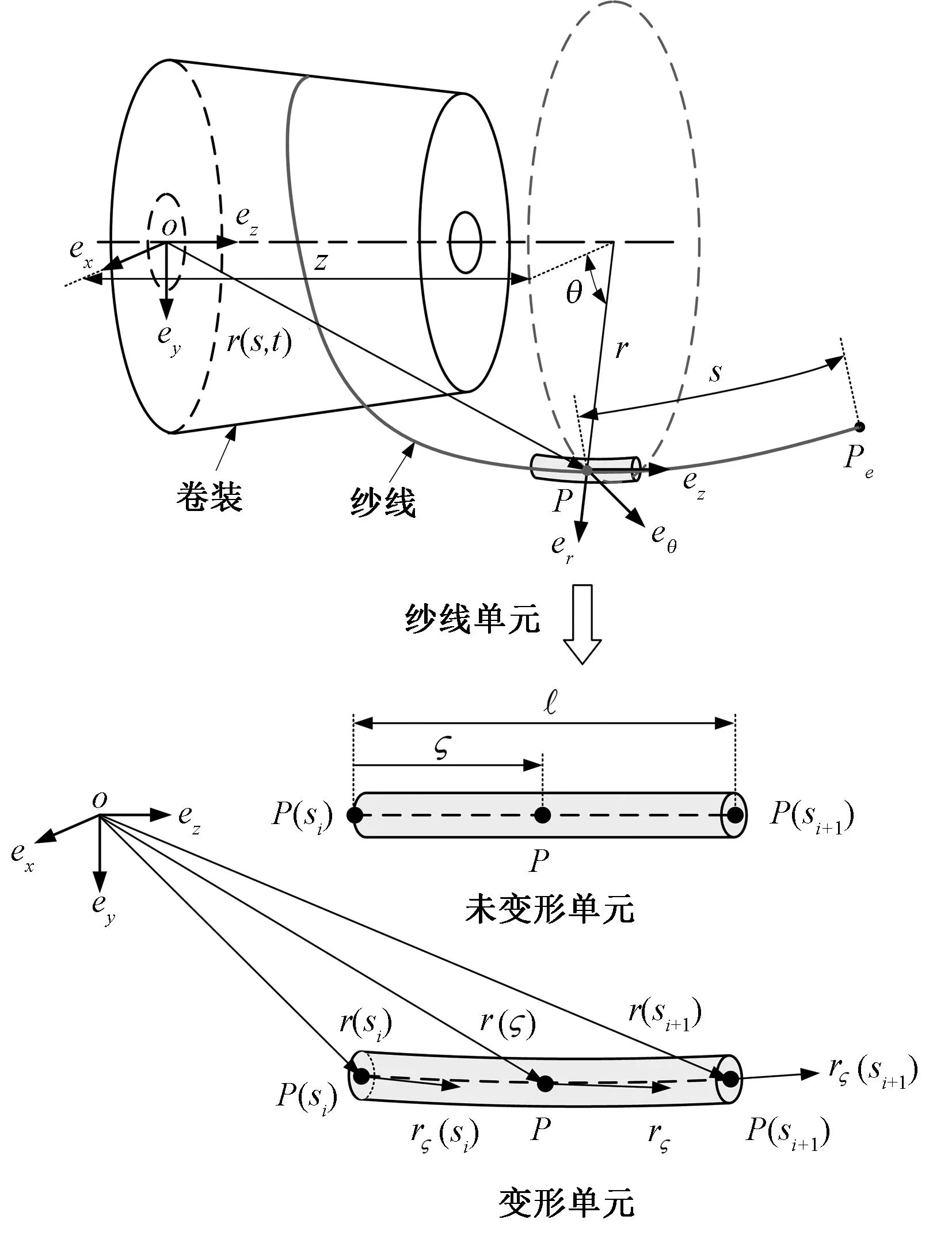
图3 运动纱线单元的ANCF模型Fig.3 ANCF model of moving yarn element

第i个纱线单元轴线上的任意点P在卷装基坐标系下的位置坐标可表示为关于物质坐标的三次多项式:

通过对单元节点左边进行三次Hermite插值,可得到P点在t时刻的全局位置坐标:

ri(,t)=S()qi(t)

式中,S()为插值基函数,即单元形函数,表示如下:

式中:I3为三阶单元矩阵;为纱线单元长度。

1.3 纱线单元广义黏弹性力

第i个纱线单元可通过轴向应变εi和曲率κi描述其轴向和弯曲变形,具体表达式如下:

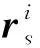
考虑纱线的黏弹性,纱线第i单元的广义黏弹性力表示为

1.4 纱线单元广义外力

其中,纱线单元的广义重力求解较为简单,由于纱线单元的每个点均受到分布载荷ρyarng的作用,ρyarn为纱线的线密度,因此纱线单元的广义重力可表示为

后文将给出纱线单元的广义空气阻力与广义接触力的求解模型。

1.4.1 广义空气阻力

当纱线在空气中运动时,纱线单元所受到的空气阻力模型如图4所示。

图4 纱线单元的空气阻力模型Fig.4 Air resistance model of yarn element

其中,t=r/|r|,b=(r×r)/|r×r|,n=b×t。忽略空气的流动速度,单位长度的空气阻力计算公式[27]如下:

式中:Cr≈1,为空气阻力系数;ρair≈1 kg/m3,为空气密度;dAcosϑ=πRdcosϑ,为纱线迎流横截面的有效面积;ϑ为v与n的夹角。

所有纱线单元均受到分布载荷dfair的作用,因此纱线单元的广义空气阻力为:

1.4.2 广义接触力

采用Hunt-Crossley模型[28]建立纱线与卷装表面的接触力模型,其可表示为

图5 纱线与卷装表面的接触模型Fig.5 Contact model of yarn with package surface

式中:zaxis=(0,0,zp-rPtanβ);Rm为卷装大端面的半径。纱线单元中与卷装表面接触的点受到集中载荷力fci(p)的作用,因此纱线单元i的广义接触力为:

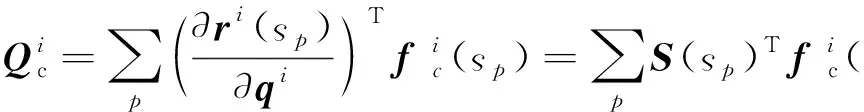
1.5 纱线运动控制方程

根据虚功原理建立纱线系统的运动控制方程。由系统各项虚功之和为零可得:

可得纱线系统的动力学微分代数方程:

对于图6所示的末端点随机械手牵引运动的卷装纱线,利用牛顿法得到纱线系统的离散动力学运动方程。首先采用全隐式积分[29]在每个时间步上更新纱线系统的广义速度:

图6 机械手牵引纱线控制示意图Fig.6 Control schematic of manipulator pulling yarn

若当前时刻机械手末端的广义坐标为p(t)=(PE,-α)T(PE和α分别为机械手末端的位置坐标与接近向量),则添加机械手运动约束后的纱线系统广义修正速度与广义坐标更新公式为

2 纱线牵引机器人避障策略

2.1 AGG-RRT算法

AGG-RRT算法是在基本RRT算法中引入了自适应目标引导分量,其原理如图7所示,图中圆形是障碍物。

图7 AGG-RRT算法示意图Fig.7 Schematic diagram of AGG-RRT algorithm

AGG-RRT算法的具体步骤为:

1) 设定起点Pstart并存储在Pnodes;

2) 在全局可行域内生成随机点Prand,并搜索Pnodes中离Prand最近的节点Pnear;

3) 沿分量PnearPrand与分量PnearPgoal的合成方向以一定步长ρ结合自适应策略生成Pnew;

4) 对路径PnearPnew进行碰撞检测,如果无碰撞,则将Pnew存储在Pnodes;

5) 重复2)～4),直至Pnew与Pgoal间的距离小于设定的误差值。

AGG-RRT算法在节点Pnear处扩展新节点Pnew的生成公式为

对应机械臂末端位置的速度公式为

式中:ρv=ρ/Δt;λ为目标引导分量系数,其被定义为

2.2 纱线轴向应变约束

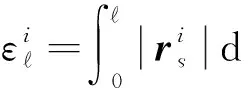
2.3 碰撞检测

通过基于纱线轴向应变约束的AGG-RRT算法得到机器人末端无碰撞路径后,需进一步对机械臂的空间构型ΩRob和纱线的空间构型Ωq与障碍物之间进行碰撞检测,以保证机械臂在牵引纱线运动过程中,机械臂体和纱线均不与环境中障碍物发生碰撞。首先使用胶囊体或球体包围盒包络不规则的机械臂和障碍物,实现模型简化。然后利用包络体之间的欧氏距离来评估机械臂与障碍物之间的空间占位关系。如果任何2个球体或胶囊之间的最小距离减去安全距离小于二者半径之和,则认为发生了碰撞。同理可评估纱线与障碍物之间的占位关系。

另外,为了保证碰撞检测的有效性,在机械臂末端每个移动间隔ΔPE内,机械臂各连杆移动的最大距离应小于最小障碍物的宽度δmax(即包络体的直径),因此机械臂末端路径的搜索步长ρ需满足以下条件。

由机械臂末端位移逆解关节转动角可得到:

Δθr=Jv(θr)(3×n)-1ΔPET

式中:θr=[θr1,θr2,…,θrn]T,为机器人的广义关节坐标;n为机器人的关节数;ωE为机器人末端的角速度向量;J(θr)(6×n)=[Jv(θr)(3×n);Jω(θr)(3×n)],为机器人末端的雅可比矩阵,它由线速度雅可比矩阵分量Jv(θr)(3×n)和角速度雅可比矩阵分量Jω(θr)(3×n)组成。

由关节转动正解关节末端位移可得到:

ΔPiT=Jvi(θri)(3×i)Δθri=Jvi(θri)(3×i)(Jv(θr)(3×i)-1ΔPET)

进一步由范数相容性有:

因此得到:

式中:ΔPi和Jvi(θri)(3×i)分别为机械人第i个关节末端的位置变化量和线速度雅可比矩阵;θri=[θr1,θr2,…,θri]T,为机器人前i个关节的广义关节坐标;Jv(θr)(3×i)为Jv(θr)(3×n)前i列的分量矩阵。

2.4 反向路径修正

机械臂沿路径Γ牵引纱线运动至Pj时,若机械臂或纱线与障碍物发生碰撞,则需对路径进行反向修正,如图8所示。首先舍弃碰撞点Pj前一点Pj-1至目标点Pgoal间的路径段;然后以Pj-1为新起点P′start至Pgoal重新逐步搜索新的无碰撞路径Γ′。需要注意的是,为防止修正路径Γ′在碰撞点Pj附近振荡,修正路径搜索时应将目标引导因子λ的初始值设为0。

图8 无碰撞路径反向修正示意图Fig.8 Collision-free path reverse correction diagram

3 模拟仿真试验

搭建小型整经纱架与移动机械臂实验平台,在SOLIDWORKS 2021内构建其URDF模型,导入MATLAB R2018a内,编写基于纱线ANCF模型与轴向应变约束AGG-RRT算法的机器人牵引纱线避障运动规划代码进行数值仿真,验证移动机械臂在复杂的纺织加工环境下对柔性纱线动态操纵规划框架的可行性。仿真在配置AMD Ryzen 7 5800H with Radeon Graphics CPU、运行频率3.20 GHz、16.00 GB内存、WIN11系统的计算机上运行。

3.1 移动机械臂建模

采用的移动机械臂由移动底盘与其搭载的六关节机械臂组成。通过MDH法对其进行运动学建模,其MDH模型与参数分别如图9和表1所示。由于移动底盘具有2个平移和1个旋转自由度,因此整个复合机械臂具有9个自由度,属于冗余度机器人,逆运动学存在多解。

表1 移动机械臂MDH参数表Tab.1 MDH parameter table of mobile manipulator

图9 移动机械臂MDH模型Fig.9 MDH model of mobile manipulator

3.2 移动机械臂避障规划

以移动机械臂从纱架正面绕至纱架背面为例,进行机器人避障路径搜索仿真,测试面对大障碍时的避障能力,仿真参数如表2所示。无碰撞路径的自动搜索结果如图10所示,对搜索的末端无碰撞路径进行2次遍历碰撞检测与修正,最终获得机器人关节空间完全无碰撞的路径。机器人绕过纱架的运动过程如图11所示。机器人移动底盘的平移运动曲线和机器人关节运动曲线分别如图12、13所示。

表2 绕过纱架路径搜索仿真参数Tab.2 Simulation parameters for path searching bypassing creel

图10 绕过纱架路径的自动搜索Fig.10 Path auto-search when bypassing creel

图11 机器人绕过纱架的运动过程Fig.11 Movement process of robot bypassing creel

图12 移动底盘的平移运动曲线Fig.12 Translational motion curves of moving chassis

图13 机械人关节运动曲线Fig.13 Joint motion curves of robot

3.3 机器人牵引纱线避障路径规划

以移动机械臂夹取卷装预留线头越过障碍将其牵引至目标点为例,进行机器人携纱路径避障仿真。仿真参数中关于路径搜索的起始与目标位姿外参数见下,其它参数均与表2中相同,纱线及卷装仿真参数见表3。

表3 机器人牵引纱线避障规划纱线和卷装仿真参数Tab.3 Yarn and package simulation parameters for obstacle avoidance planning of robot

另外纱线ANCF模型的单元数为172,每个单元未变形情况下的初始长度为11.8 mm,纱线的一侧端点与卷装固连。纱线所有单元的整体轴向应变最大值εmax设为1 mm。

纱线无碰撞牵引路径的自动搜索结果如图14所示,对搜索的末端无碰撞路径进行8次遍历碰撞检测与修正,最终获得机器人关节空间完全无碰撞的纱线牵引路径。机器人移动底盘的平移运动曲线和机械人的关节运动曲线分别如图15、16所示。

图14 纱线牵引路径自动搜索Fig.14 Automatic search of yarn-pulling path

图15 纱线牵引路径移动底盘的平移运动曲线Fig.15 Translational motion curves of moving chassis for yarn-pulling path

图16 纱线牵引路径机械人关节运动曲线Fig.16 Joint motion curves of robot for yarn-pulling path

进一步对移动机械臂的无碰撞路径在笛卡尔坐标系内进行S型速度曲线规划[26],得到如图17所示的机器人携纱运动的插补轨迹。然后根据纱线的运动控制方程,求解每个机器人运动时间步长下纱线的空间构型,其结果如图18所示。另外图19示出纱线第40、80、120和160单元的整体轴向应变,可以看出,各单元的整体轴向应变的绝对值均小于εmax(1 mm),避免了纱线被过度拉伸,满足了机器人对纱线的柔顺牵引。

图17 机器人牵引纱线路径S型速度插补轨迹曲线Fig.17 S-shaped velocity interpolation trajectory curves for robot yarn-pulling path

图18 机器人牵引纱线避障运动过程Fig.18 Obstacle avoidance motion process of robot pulling yarn

图19 部分纱线单元的整体轴向应变Fig.19 Overall axial strain of some yarn elements. (a) 40th yarn element; (b) 80th yarnelement; (c) 120th yarn element; (d) 160th yarnelement

4 结 论

本文针对机器人在复杂纺织加工环境中对柔性线形纱线直接操纵存在纱线形态感知困难和机器人运动空间受限的两大难点,以移动机械臂对织造前整经纱架上卷装线头的牵引操纵为例,提出了一种集成移动机械臂运动规划策略的卷装纱线牵引操纵控制框架。构建了卷装纱线系统的动力学模型;解析了机器人与纱线间的运动耦合关系和机器人牵引纱线的运动控制方程;提出了基于纱线轴向应变约束的改进自适应引导快速扩散随机树算法,以此对移动机械臂进行了避障运动规划,绕开环境障碍的同时防止纱线被过度拉伸。

在仿真实验中,首先对移动机械臂绕过纱架进行了模拟,验证了避障算法面对大障碍物的避障能力,表明该算法在复杂的纺织加工环境下具有适用性。然后对移动机械臂牵引纱线绕过障碍物到达目标点进行了模拟,成功规划出无碰撞轨迹,并有效控制了纱线被牵引运动过程中的轴向应变,表明该控制框架的有效性,能够满足机械臂对卷装纱线从起点到目标点的无碰撞柔顺牵引操纵需求。