模糊条件下考虑低排放和可折叠箱的空箱调运优化研究

袁雪丽，杨菊花

(兰州交通大学 交通运输学院，甘肃 兰州 730070)

0 引言

国际经济贸易的繁荣发展促进了国内外商品的快速流通，在经济全球化的大背景下，集装箱海铁联运以箱为运输单位，简化货运作业手续，凭借其高效率、快周转、高效益、高协作的优点，成为国际物流的主要运输组织方式。由于国内外各个地区经济发展水平的差异性及资源分布的不均衡性，导致各站点和港口间集装箱供需的不平衡，因此加强集疏运系统，提高运输效率对于满足各站点的空箱需求具有现实可行的研究意义。

对于集装箱空箱调运的动态性、随机性和模糊性，肖青等[1]综合考虑空重箱联合运输及重箱需求的模糊性，研究不同成本对运输方案的影响；韩晓龙等[2]针对空箱需求的不确定性，以调运成本和公司信誉成本的加权和为目标，突出联合优化调运方案的优越性；常空[3]采用模糊库存管理模型，确定各集装箱办理站最优空箱调运量；Sarmadi等[4]以加速Benders 分解算法，求解考虑需求随机性的集装箱运输和库存动态联合模型。为实现可持续发展，构建绿色交通运输体系，国内外学者在集装箱运输过程中减少碳排放方面取得一定的研究成果。徐华锋等[5]基于低碳运输服务网络，提出共享模式下的空箱调运模型；赵祎[6]考虑随机空箱需求、随机空箱供给和二氧化碳排放，求得高效低碳的海铁联运空箱调运方案；Gao等[7]考虑碳税和货主选择惯性，建立双层规划模型，优化集装箱海运运输网络；Wang等[8]以运行周期内二氧化碳排放成本、航次运输成本和托运人库存成本最小为目标，求解低碳环境下集装箱班轮作业的最优航行频率和船型；刘倚玮等[9]考虑碳排放成本对多目标集装箱运输组织方式进行优化。在延缓全球变暖的趋势下仅考虑二氧化碳的排放并不全面，因此在借鉴以上研究的基础上加入海运过程中硫气体的排放。

为降低运输成本，提高设备利用率，近年来可折叠集装箱逐渐投入运用。邢磊等[10]建立鲁棒机会约束规划模型研究中欧班列空箱调运，得出选用适当比例的可折叠集装箱可以降低运输总成本；林丹英[11]考虑服务软时间窗和碳排放成本，分析海陆联运中可折叠集装箱对于成本的优化；张瑞友等[12]将时间窗引入可折叠箱的接驳运输问题，利用主动式禁忌搜索算法进行求解；Zhang 等[13]考虑桥梁高度和水深约束，得出可折叠集装箱能够更有效地利用船舶空间，降低运输总成本。因此，研究将可折叠集装箱纳入空箱调运问题的研究范畴。

目前空箱调运问题多集中于单一运输方式，且大多数为仅考虑成本最低的单目标规划，很少兼顾到运输过程中温室气体的排放；求解方式也多采用LINGO求解器和CPLEX，缺乏启发式算法的应用。研究在考虑降低碳、硫气体排放的前提下，分析铁路和海洋2 种运输方式间的集装箱空箱调运问题，为保证运输效率、提高运输效益，部分空箱采用可折叠式。将空箱需求和供给利用梯形模糊数进行模糊化处理，建立多目标空箱调运模糊机会约束规划模型，采用非支配排序遗传(NSGA-Ⅱ)算法进行求解分析，致力于达到总的运营成本最少和碳、硫气体排放量最低，实现运营效益和环境保护的共赢。

1 问题描述

基于铁路和海洋2 种运输方式，研究多个计划期内我国内陆港口和各个集装箱办理站之间的空箱调运问题，空箱调运方向图如图1 所示。运输情景分为2 种，情形1 仅考虑标准空箱的调运问题，情形2 则采用标准箱和可折叠箱混合调运的模式。在不影响运输时效性的前提下做出如下假设。①标准箱均采用20 ft 集装箱，为一个标准TEU，40 ft 集装箱等同为2 个20 ft 集装箱；②考虑就地租箱原则，标准集装箱采用租用方式，可折叠集装箱采用购买方式；③空箱调运在一个计划期内可以完成，租箱数量和归还期限不受限制；④各集装箱办理站和港口初始库存量均为0；⑤每个计划期各节点的空箱需求量均被满足。

图1 空箱调运方向图Fig.1 Transportation direction of empty containers

2 模型构建

2.1 符号说明

A：车站集合，i，j∈A。

V：港口集合，p，q∈V。

λ：∀p，q，i，j。

t：计划期。

α，β，γ，ε：置信水平，取值范围为[0，1]。

，：t期从港口p运往港口q的单位标准集装箱/可折叠集装箱单位公里运输费用，元/(TEU·km)。

，：t期从港口p运往集装箱办理站j的单位标准集装箱/可折叠集装箱单位公里运输费用，元/(TEU·km)。

，：t期从集装箱办理站i运往港口q的单位标准集装箱/可折叠集装箱单位公里运输费用，元/(TEU·km)。

，：t期从集装箱办理站i运往集装箱办理站j的单位标准集装箱/可折叠集装箱单位公里运输费用，元/(TEU·km)。

，：t期从港口p运往港口q的标准集装箱量/可折叠集装箱量，TEU。

，：t期从港口p运往集装箱办理站j的标准集装箱量/可折叠集装箱量，TEU。，：t期从集装箱办理站i运往港口q的标准集装箱量/可折叠集装箱量，TEU。

，：t期从集装箱办理站i运往集装箱办理站j的标准集装箱量/可折叠集装箱量，TEU。

dpq，dpj：港口p到港口q/集装箱办理站j的运输距离，km。

diq，dij：集装箱办理站i到港口q/集装箱办理站j的距离，km。

ypq：0-1 变量，是否先挂靠港口p再挂靠港口q，如果是则为1，否则为0。

ypj：0-1 变量，港口p和集装箱办理站j之间是否连通，如果是则为1，否则为0。

yiq，yij：0-1变量，集装箱办理站i和港口q/集装箱办理站j之间是否连通，如果是则为1，否则为0。

，：t期港口p/集装箱办理站i单个集装箱的装箱成本，元/TEU。

，：t期港口q/集装箱办理站j单个集装箱的卸箱成本，元/TEU。

，：t期港口q/集装箱办理站j单个标准集装箱的租箱成本，元/TEU。

，：t期港口q/集装箱办理站j单个可折叠集装箱的购买成本，元/TEU。

，：t期港口q/集装箱办理站j的标准箱租箱数量，TEU。

，：t期港口q/集装箱办理站j的可折叠箱购箱数量，TEU。

，：t期港口λ或集装箱办理站λ单个标准集装箱/可折叠集装箱的存储成本，元/TEU。

，：t期港口λ或集装箱办理站λ所存标准箱/可折叠集装箱数量，TEU。

，：单位标准箱/可折叠集装箱每公里的海运碳排放量，kg/(TEU·km)。

，：单位标准箱/可折叠集装箱每公里的海运硫排放量，kg/(TEU·km)。

，：单位标准箱/可折叠集装箱每公里的铁路运输碳排放量，kg/(TEU·km)。

Ec，Es：海洋运输单位标准箱碳/硫排放限制量，kg/TEU。

，：海洋运输单位可折叠集装箱碳/硫排放限制量，kg/TEU。

m，mF：船舶运输标准箱/可折叠集装箱数量，TEU。

Uc，：铁路运输单位标准箱/可折叠集装箱碳排放限制量，kg/TEU。

η：铁路区段路面颠簸系数和海面状况波动影响系数。

，，，：港口λ或集装箱办理站λ单位可折叠集装箱折叠成本/展开成本/折叠量/展开量，元/TEU。

，：t期/t- 1 期港口λ或集装箱办理站λ的库存量，TEU。

，：t期港口λ或集装箱办理站λ的空箱供给量/需求量，为模糊变量，TEU。

：港口λ或集装箱办理站λ的最大存储量，TEU。

n：一个标准集装箱的体积折合为可折叠集装箱后的个数，n= 4。

2.2 目标函数及约束条件

（1）情景1：标准空箱调运问题。仅考虑标准集装箱空箱调运问题的目标函数、约束条件如下。公式⑴为第1 个目标函数，C1表示情景1 下计划期内运营总成本最小，包括空箱调运成本、装卸成本、租箱成本和存储成本；公式⑵为第2 个目标函数，C2表示情景1 下整个调运过程中铁路运输产生的二氧化碳和船舶航行排放的碳和硫气体之和最小。

（2）情景2：标准箱与可折叠箱组合调运问题。考虑标准集装箱和可折叠集装箱2 种箱型空箱调运问题的目标函数、约束条件如下。情景2 与情景1的区别在于目标函数和约束条件中考虑了可折叠集装箱的调运和由此产生的折叠和展开成本，情景2的目标函数为公式⒃和⒄，约束条件为公式⑶至⑽、公式⑿至⒂和公式⒅至。表示情景2 下计划期内运营总成本最小，包括空箱调运成本、装卸成本、租箱成本和存储成本；表示情景2 下整个调运过程中铁路运输产生的二氧化碳和船舶航行排放的碳和硫气体之和最小。

3 模型转化

3.1 不确定理论相关定义

（1）定义1：假设x为决策向量，ζ为参数向量，f(x，ζ)为目标函数，gj(x，ζ)为约束函数，j=1，2，……，p。希望约束条件以一定的置信水平α成立，即有机会约束[14]。

（2）定义2：梯形模糊变量为由清晰数构成的一个四元组(a，b，c，d)，a≤b≤c≤d。其隶属函数μ(x)如公式所示，模糊变量的可信性分布如公式所示［14］。隶属函数图如图2所示。

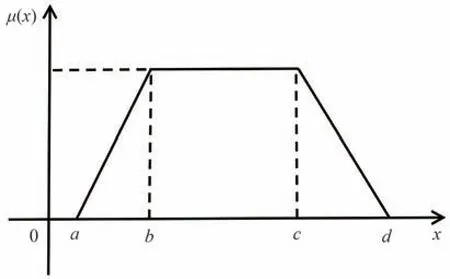
图2 隶属函数图Fig.2 Membership function

根据可信性分布可以求出梯形模糊变量的期望值如下。

（3）定义3：设梯形模糊数A=(a1，a2，a3，a4)，B=(b1，b2，b3，b4)， 且a1≤a2≤a3≤a4，b1≤b2≤b3≤b4，则其加减乘除运算法则分别表示如下[3]。

（4）定义4：利用以下方法将模糊规划约束转化为线性约束[15]。当且仅当(1 -ε)a+εb≤z时，Pos{͂≤z}≥ε；当且仅当(1 -ε)d+εc≥z时，Pos{͂≥z}≥ε；当且仅当(1 -ε)a+εb≤z且(1 -ε)d+εc≥z时，Pos{͂=z}≥ε。

3.2 确定模型转换

4 算法设计

研究采用NSGA-Ⅱ算法求解多目标空箱调运问题，对于染色体的编码、交叉和变异等主要算法步骤进行如下阐述。

（1）染色体编码及初始化种群。采用矩阵编码方式，以矩阵X表示。由于研究案例中为不平衡运输，因而在染色体矩阵中增加一行虚拟供给站点用于表示租箱的数量，增加一列虚拟需求站点用于表示存储的数量。通过增加虚拟需求站点和虚拟供给站点把不平衡运输问题转化为平衡运输问题，然后通过随机化的西北角法产生初始种群。

式中：xij为染色体的基因，i∈[1，n]，j∈[1，m]，表示由第i个站点运往第j个站点的集装箱空箱数量。

（2）交叉算子。随机选取2 个个体作为父项X1，X2，并将X1，X2对应元素相加后取平均值，平均值整数部分和余数部分分别用矩阵D和R表示，矩阵R行和列中元素为1 的个数之和都为偶数，因而把矩阵R分解为2 个子矩阵R=R1+R2，则2 个新个体就为X3=D+R1，X4=D+R2。

（3）变异算子。采用基于矩阵闭合回路法设计遗传算子，在染色体矩阵X中随机挑选2 个不同行不同列的非零元素xi0j0，xi1j1，取令xi0j0=xi0j0-δ，xi1j1=xi1j1-δ，xi0j1=xi0j1+δ，xi1j0=xi1j0+δ，其余基因取值不变，组成新的染色体。

5 案例分析

5.1 研究数据

选取3 个集装箱港口和12 个集装箱办理站的输送网络进行研究，运输线路图如图3 所示。计划周期数为3，每个计划周期长为1 d。标准集装箱采用租赁方式、可折叠集装箱采用购买方式。可折叠集装箱的折叠展开成本均为30 元/TEU。各城市节点初始空箱量为0，最大库存量不超过800 TEU，港口最大存储容量为1 500 TEU，支线船的容量为700 TEU。数据说明如表1 所示，模糊条件下空箱需求量如表2 所示，模糊条件下空箱供给量如表3所示。

表1 数据说明表Tab.1 Data specification

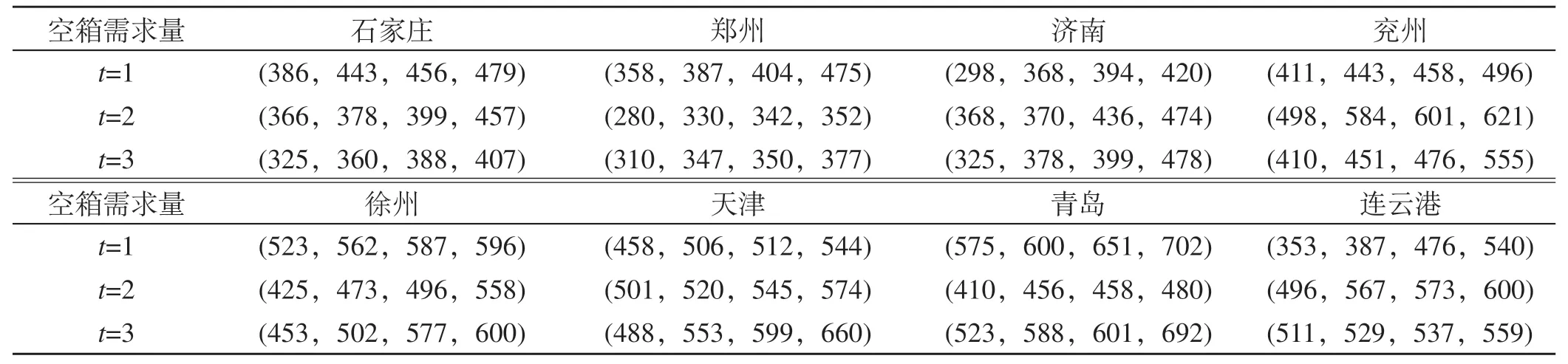
表2 模糊条件下空箱需求量TEU Tab.2 Demand for empty containers under fuzzy conditions

表3 模糊条件下空箱供给量TEU Tab.3 Empty container supply under fuzzy conditions

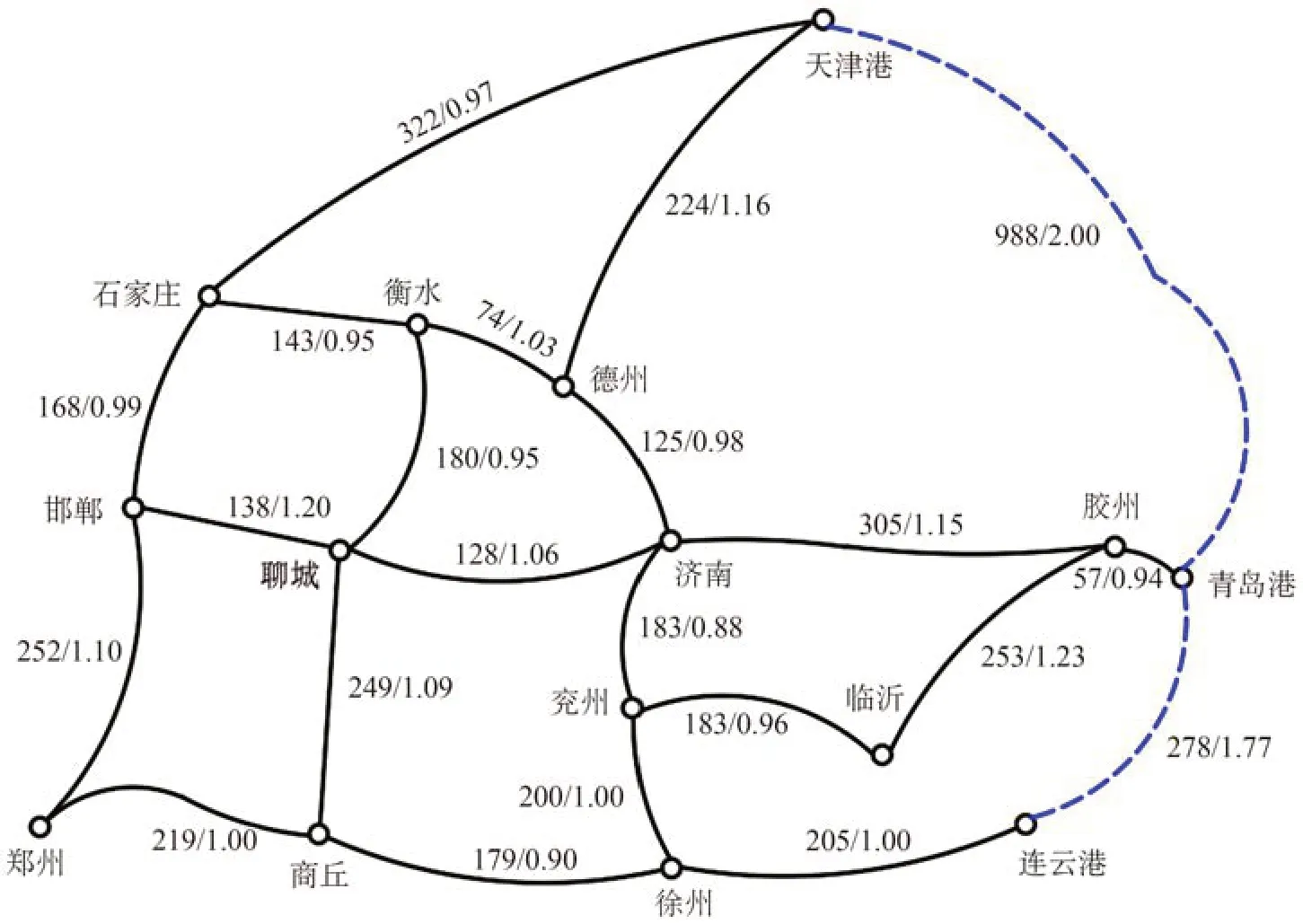
图3 运输线路图Fig.3 Transportation route

5.2 计算结果分析

使用数学软件进行求解，其中种群大小设为30，最大迭代次数为500 次，交叉概率取为0.65，变异概率取0.1。置信水平取α= 0.95，β= 0.85，γ=0.9，ε= 0.8。

5.2.1 情景1只使用标准集装箱

采用海铁联运的运输组织模式，求得只使用标准集装箱情况下的Pareto 解集如表4 所示，Pareto解集运输方案如表5 所示。由表4 和表5 可知不同运输方案的各个子目标值相差不大，因而在某条线路列车运能紧张或者海运船舶运能紧张的情况下，运输部门可以根据不同方案灵活安排运输箱数，尽可能地在最短时间内满足各个站点的空箱需求量。

表4 Pareto解集Tab.4 Pareto solution set

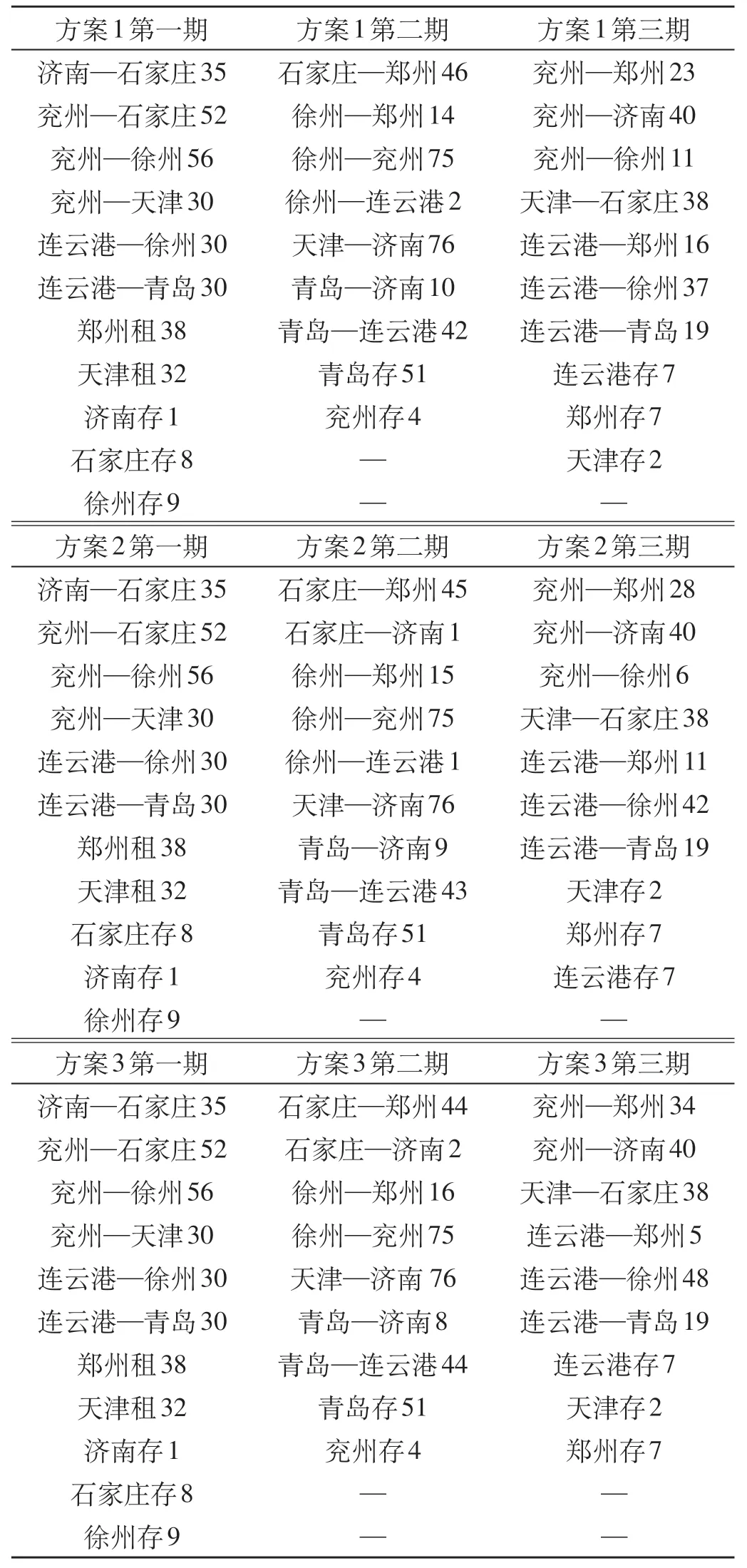
表5 Pareto解集运输方案TEUTab.5 Transportation scheme of Pareto solution set

对比纯铁路运输和海铁联运2 种不同的运输组织模式，纯铁路运输和海铁联运比较分析如表6 所示。从表6中可得海铁联运模式下的2个子目标均值较纯铁路运输分别优化了7.66%和6.98%，节省运营总成本26 221.60元，降低碳硫气体量6 861.49 kg，突出了海洋运输运营成本低、温室气体排放量少的明显优势。同时海洋运输运量大，不受道路限制，灵活性较高，因而大力发展海铁联运是中西部地区进行空箱调运和进出口货物的较优选择。

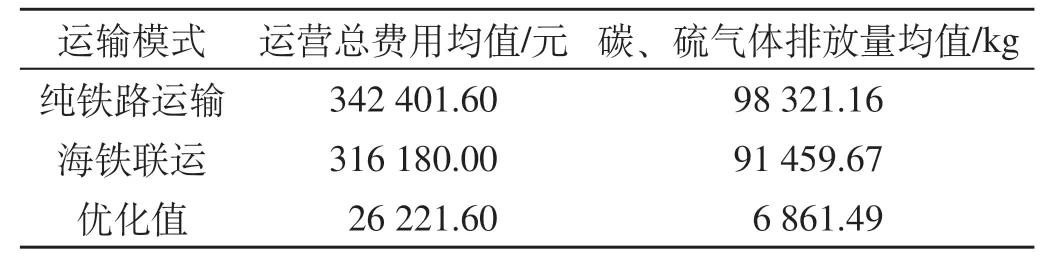
表6 纯铁路运输和海铁联运比较分析Tab.6 Comparative analysis of pure railway transportation and sea-rail intermodal transportation

5.2.2 情景2 标准集装箱和可折叠集装箱混合运输

对于可折叠集装箱所占比例分别取不确定需求和供给的30%~70%，步长取10%，分别计算不同比例下的运输费用、装卸费用、堆存费用、购箱费用、折叠展开费用、运营总费用和碳、硫气体排放量。绘制图形直观表示，可折叠集装箱不同比例下的费用如图4 所示，可折叠集装箱不同比例下的气体排放如图5 所示。从图4 中可以看出可折叠集装箱所占比例为30%时总的费用达到最低，购箱费用随着可折叠集装箱所占比例的增大出现明显的递增趋势，呈现一定的正比关系，显然购箱成本是影响可折叠集装箱使用的关键因素。由图5 可得使用39%~45%的可折叠集装箱可以降低碳和硫气体的排放量，增强环境保护度，其中可折叠集装箱的比例为40%时碳、硫气体排放量最低。

图4 可折叠集装箱不同比例下的费用Fig.4 Costs of foldable containers at different proportions

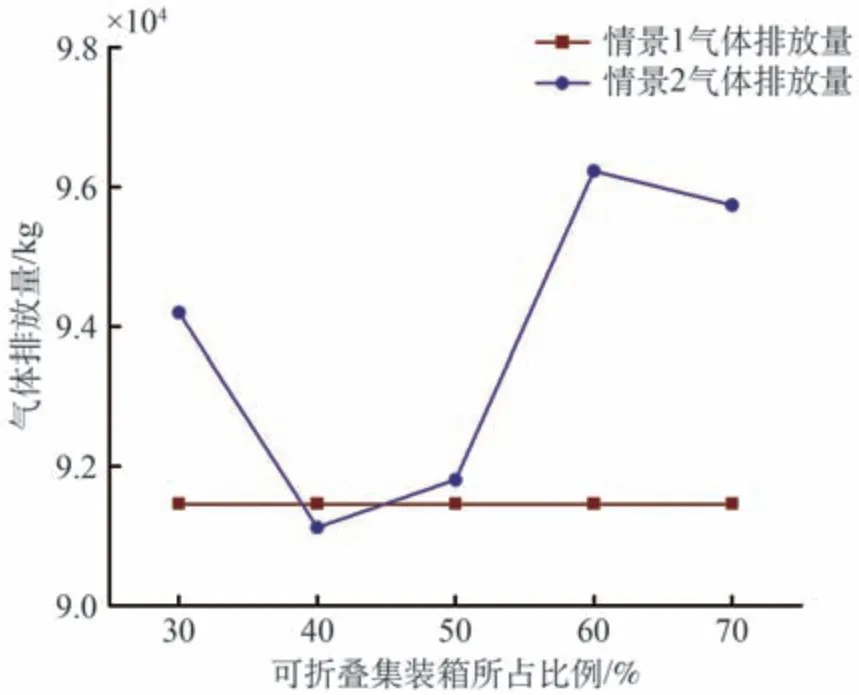
图5 可折叠集装箱不同比例下的气体排放Fig.5 Gas emissions of foldable containers in different proportions

如果降低可折叠集装箱的购买成本，分别降为原购买成本的10%~90%，并与运输全标准箱的费用进行对比分析，绘制图形进行直观表示。费用比较如图6 所示。由图6 可知，当购买成本降低到一定的费用后，实行一定比例的可折叠集装箱和标准箱混合运输组织模式的运营总费用较全标准箱运输组织模式更低。费用相对偏差如表7 所示，从表7中可以得到费用相对偏差小于0 的方案都能实现比运输全标准箱更低的经济成本，费用偏差越小说明混合运输模式费用也就越低。例如，选用40%的可折叠箱，降低其购买成本至原成本的10%~50%都能实现比运输全标准箱更低的运营总费用，同时运输40%可折叠箱的气体排放量也低于运输全标准箱。因此，可折叠箱的购买成本在总费用中占比较大，如果能够适当降低其造价成本，运输一定比例的可折叠箱可以实现运营总费用、运输效率、环境保护的共赢。

表7 费用相对偏差Tab.7 Relative cost deviation

图6 费用比较Fig.6 Cost comparison

6 研究结论

研究从标准集装箱入手，结合可折叠集装箱，建立考虑运营总费用最小和碳硫气体排放量最少的多计划期双目标规划空箱调运模型，将运营总费用划分为运输费用、装卸费用、堆存费用、租箱费用和可折叠箱的折叠展开费用，采用NSGA-Ⅱ算法进行求解后可得如下结论。

（1）在采用全标准箱的运输组织模式下，运输费用是影响运营总费用的主要因素。多目标规划为运输部门提供了多种切实可行的运输方案，更为符合现实状况的发展。同时，海铁联运模式的运营总成本和温室气体排放量均小于纯铁路运输，因而后续发展应调整运输结构，加大集装箱海铁联运的比例。

（2）在混合运输组织模式下购买成本是影响可折叠集装箱使用的关键因素，一定程度上降低购买成本，采用标准箱和可折叠箱混合运输可以实现更低的运营总费用，在提高运输效率的同时还能够减少碳和硫气体的排放，形成绿色可持续的交通运输体系。

（3）后续可以从如何降低可折叠集装箱的购买成本和影响购买成本的因素入手进行研究，同时考虑空重箱的协同运输更为符合现实发展状况。