基于适箱货物优先级的铁路空箱调运模型＊

段 刚，陈 莉，陈志忠，李引珍，刘玉胜，杨欣翥

(1.兰州交通大学交通运输学院，甘肃兰州 730070;2.兰州城市学院数学学院，甘肃兰州 730070;3.兰州交通大学机电工程学院，甘肃兰州 730070)

基于适箱货物优先级的铁路空箱调运模型＊

段 刚1，陈 莉2，陈志忠1，李引珍1，刘玉胜2，杨欣翥3

(1.兰州交通大学交通运输学院，甘肃兰州 730070;2.兰州城市学院数学学院，甘肃兰州 730070;3.兰州交通大学机电工程学院，甘肃兰州 730070)

根据铁路运输的特点，将适箱货物按重要程度分为不同的优先等级，建立铁路集装箱空箱调运非线性混合整数规划模型。目标函数为极小化空箱调运费用，在空箱量不足的条件下，首先满足各站高等级货物的空箱需求，并只有在高等级货物空箱需求得到满足且仍有空箱时，才会考虑各站低等级货物的空箱需求。数值算例验证了模型的有效性和可行性。

集装箱空箱调运;货物优先级;混合整数规划

由于我国自然资源分布不平衡，受地区经济发展和城市布局等因素的影响，全国集装箱货源分布和流向存在着很大差异，导致铁路集装箱供需矛盾十分突出，空箱调运较为频繁。据统计［1］，2008年回送铁路空箱819 128标准箱(TEU)，占发送铁路箱数的42.6%，比2007年增加13 216标准箱(TEU);到达铁路空箱984 674标准箱(TEU)，占到达铁路重箱的55.4%，比2007年增加6 707标准箱(TEU)。这无疑给铁路运能造成了极大的浪费，所以合理而高效地调配铁路空箱对减少运输成本、促进集装箱运输的发展至关重要。

1 国内外研究现状

Feng等［2］运用收益管理模型为亚洲船运公司的特定航线制定了空箱最优舱位分配方案，以极大化船运公司经营利润为目标，同时考虑空箱分配的期望成本，以船舶容量、集装箱需求和空箱供应为约束条件建立数学模型。Moon等［3］研究了空箱最优分配以减少港口之间集装箱的不平衡性，目标极小化以及运输费用，处理费用和持有费用为代表的总成本。同时构造了混合整数规划模型，对采购及租赁集装箱的数量进行了研究，并采用混合遗传算法求解。Chou等［4］建立了混合模糊决策模型，将空箱配送问题分为2个阶段:第1阶段，应用模糊缺货存贮模型，将最优缺货量作为一港口的最优租箱量，将最优定货量作为一个港口的最优空箱需求量;第2阶段，采用网络模型，基于以上2个最优结果，优化了多个港口之间的空箱调运问题。Song等［5］考虑了动态与随机环境下的空箱配送问题，将其划分为空箱装载与卸载2个部分，制定了一个灵活的配送策略:即空箱配送的目的地和数量事先不确定，而是在途中根据港口最新的即时信息来确定。在贸易不均衡情况下明显优于传统优化方法，成本可以降低22%。灵敏度分析表明这一优势受贸易不平衡方式、船队规模和边界值因素的影响很大，但对需求分布类型和船舶容量并不敏感。

段刚等［6］针对一般空箱调运问题设计了遗传算法，采用整数矩阵编码，通过对父代染色体的线性组合取整运算作为交叉算子，并做适当调整以保证解的可行性，同时利用矩形闭合回路调整调运量作为变异算子，该算法可以高效求解空箱调运问题。闫海峰等［7］根据集装箱班列开行特点，以混合箱流的输送时间、距离和费用三者的综合最优为目标，建立了结点站间基于径路选择的空箱调配混合0－1规划模型，将模型模拟为一个二级耦合反馈系统来设计算法求解。朱德辉等［8］对罐式集装箱重箱流和空箱流调配进行了综合优化，以罐箱运输费用最小为目标，建立铁路罐式集装箱空箱调配优化多商品网络流模型，并构造了一种嵌入模拟退火操作的遗传算法对之进行求解。张得志等［9］从铁路集装箱运输市场的实际情况出发，建立了基于顾客偏好的模糊运输规划模型和带时间窗的运输规划模型，并应用遗传算法对其求解。彭华等［10］以最大限度地提高区域内空箱的利用率和减小空箱调度的成本为目标，建立了在一个计划期内的铁路集装箱空箱动态优化调度模型，运用遗传算法对模型进行求解，解决了在一个计划期内，如何最优化地对每个工作日的空箱进行区域性调度的问题。

与空车调运类似，铁路集装箱办理站首先应使用本站卸空箱满足适箱货物需求。当一个车站的装箱数大于卸空箱数时，就需要接入空箱，相反则排出空箱。但由于集装箱数量有限，难以满足全部货物空箱需求，因此由哪些空箱供应站向哪些空箱需求站调运空箱，调运数量是多少就成为优化的核心问题。

铁路运输遵循先计划内后计划外，先重点后一般，先中央后地方的原则，其核心是在保证重点物资运输的基础上分别轻重缓急，全面统筹安排运输任务。本文基于此要求，将适箱货物按重要程度分为不同的等级，在空箱调运方案中，首先考虑满足高等级货物的空箱需求，并只有在高等级货物空箱需求得到满足后且仍有空箱时，才会考虑低等级货物的空箱需求。

2 模型

2.1 假设条件

将适箱货物优先等级p从小到大排序，序号越小等级越高，调配空箱时优先满足，且只有高等级的适箱货物空箱需求得到满足后，才会考虑低一等级的适箱货物空箱需求。优先等级的划分依据主要是货物的品种和重要程度等，比如关系国计民生，涉及国际声誉，军运、抢险救灾等重点物资拥有较高的优先级。因为要按照货物优先等级运输，所以即使某站的卸空箱能满足高等级的货物需求，且仍有剩余空箱，但若其他站仍有高等级适箱货物没有得到空箱满足，该空箱需求站将会向其他空箱需求站调运空箱。

2.2 参数与决策变量设置

参数设置如下:

S为空箱供应站集合，S={1，2，…，m};D为空箱需求站集合，D={m+1，m+2，…，m+n};p为适箱货物等级，p=1，2，…，P为j站p等级的适箱货物所需空箱数，p=1，2，…，P，j∈D;ai为i站已有空箱数，i∈S;dj为j站卸空集装箱数，j∈D;cij为i站调运到j站一个空箱的成本，i∈S∪D，j∈D，i≠j;s0为虚设的空箱供应站，当某些需求无法满足时，由该站提供，其中c0j=0，a0=

决策变量:

站向j站调运满足p等级适箱货物的空箱数，i∈S∪D，j∈D，i≠j，p=1，2，…，P。

2.3 模型

2.3.1 目标函数

目标为调运费用的极小化。

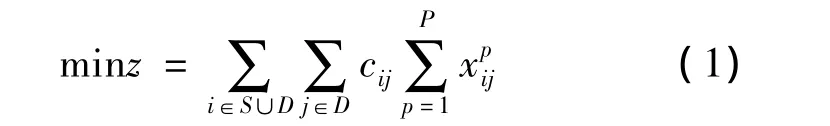
2.3.2 约束条件

(1)空箱供应与需求满足平衡

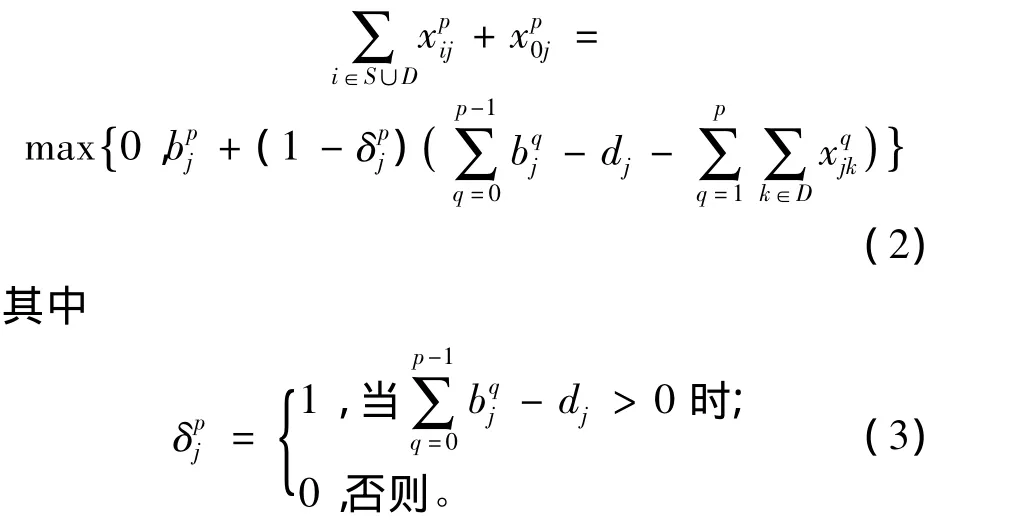
(2)式和(3)式中都有j∈D，p=1，2，…，P，并规定b0j=0。每个空箱需求站首先利用本站卸空箱装运高等级的适箱货物，如果卸空箱数不能满足高等级适箱货物空箱需求，可以考虑从空箱供应站调运，也可以从其他空箱需求站调运，如果适箱货物等级较低，无法得到满足，则需从虚设供应站调运;反之，当卸空箱数多于高等级适箱货物空箱需求时，则该站可以向其他空箱需求站调运空箱;

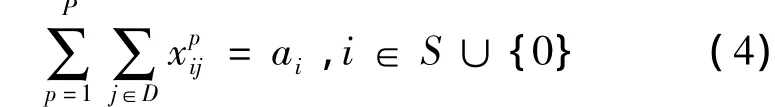
空箱供应满足平衡，包括虚设供应站;

(2)适箱货物等级之间的关系

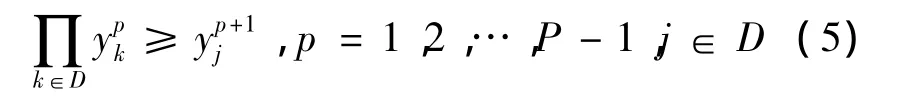
只有当所有站的高等级适箱货物空箱需求得到满足后，才会考虑j站低一等级空箱需求;

(3)空箱需求量与适箱货物等级的关系

其中M为非常大的数(下同)，p=1，2，…，P;若全部卸空箱数与可供应空箱数之和不小于所有需求站p等级货物空箱需求之和，则所有需求站p等级的空箱需求都能得到满足，反之不会都得到满足;

(4)j站p等级货物所需空箱数能否得到满足的条件

(7)式保证当j站p等级货物需求得到满足时，虚设供应站不能向j站提供空箱;或者虚设供应站向j站提供空箱时，j站p等级货物需求不会得到满足;(8)式为第一等级货物需求能否得到满足的条件;(9)式保证当虚设供应站不向j站提供空箱，且所有站高一等级货物需求没有同时得到满足时，j站p等级货物需求也不会得到满足，即= 0;当虚设供应站不向j站提供空箱，且所有站高一等级货物需求同时得到满足时，j站p等级货物需求得到满足，即= 1;

(5)需求站之间的空箱调运

当j站卸空箱数大于该站p等级货物空箱需求，k站卸空箱数小于该站p等级适箱货物空箱需求，且k站p等级适箱货物空箱需求必须满足的条件下，j站可以向k站调运p等级空箱;

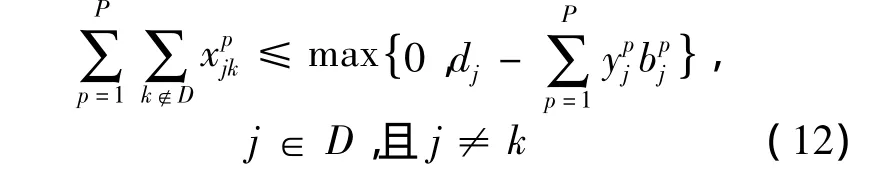
j站向其他所有空箱需求站调运全部等级空箱数，应不超过该站卸空箱数与满足该站高等级适箱货物空箱需求空箱数之差;

空箱调运不对流，即对空箱需求站j而言，到达的空箱与发出的空箱二者至少有一种为零;

(6)变量的约束

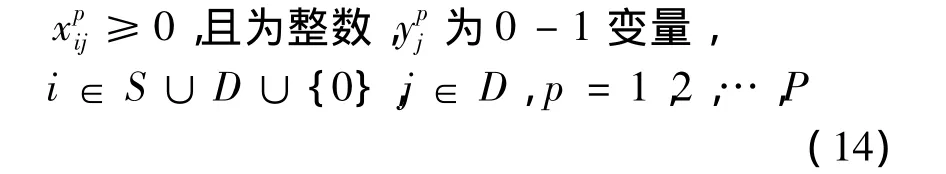
3 算例

设有3个空箱供应站，4个空箱需求站，1个虚设供应站，货物等级分为3等，供应站空箱供应量见表1，需求站卸空箱数见表2，空箱需求站各等级货物需求空箱数见表3，空箱供应站与需求站间单位空箱运费见表4，空箱需求站间调运单位空箱运费见表5。取M=100，采用LINGO9.0软件对模型求解。最优空箱调运方案见表6。

表1 供应站空箱供应量/箱Table 1 Empty container supply level in supply station

表2 需求站卸空箱数/箱Table 2 Unloading container level in demand station

表3 空箱需求站各等级货物所需空箱数/箱Table 3 Empty container level of different cargo rank in demand station

表4 空箱供应站与需求站间单位空箱运费/元·箱－1Table 4 Unit empty container transportation cost between supply station and demand station

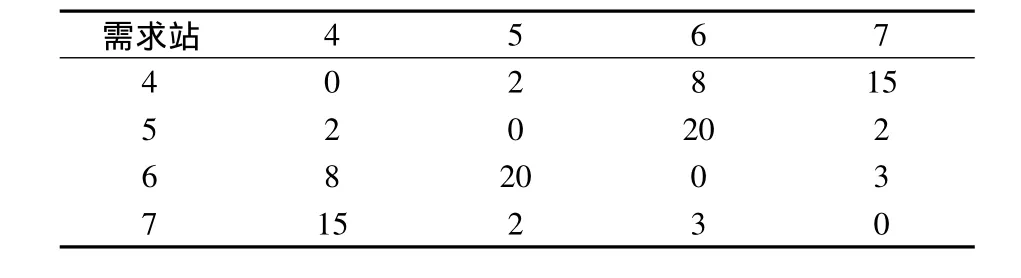
表5 空箱需求站间单位空箱运费/元·箱－1Table 5 Unit empty container transportation cost between demand stations

表6 最优空箱调运方案/箱Table 6 The best empty container transportation scheme

从最优解表6中不难看出，需求站4的全部等级货物，需求站6和7的第1等级货物由本站卸空箱提供，需求站7的第2等级货物由本站卸空箱和供应站3共同满足。需求站5和7的第3等级货物所需空箱没有得到满足(由虚设供应站0提供)。由于需求站4的卸空箱数大于各等级的货物所需空箱数，所以多余的空箱被调运到需求站5满足该站第2等级货物需求。在严格按照货物优先等级运输的基础上，实现了调运费用的最小，为174。

4 结语

(1)基于铁路运输全面统筹安排运输任务的特点，将适箱货物按重要程度分为不同的等级，在集装箱数量不足的条件下，优先考虑高等级适箱货物的空箱需求。

(2)在本站卸空箱不足情况下，其高等级货物空箱需求由空箱供应站或其他低等级适箱货物空箱需求站卸空箱负责排空，这样就可以保证重点物资优先得到空箱。

(3)算例表明，基于适箱货物优先等级的铁路空箱调运模型可以有效地得到优化方案，满足铁路运输的需要，为铁路运输提供科学合理的解决方案。

［1］施亚萍.提高铁路集装箱空箱调配效率的思考［J］.铁道货运，2009(6):39－41.

SHI Ya-ping.Thinking on improving efficiency of railway empty container allocation［J］.Railway Freight Transport，2009(6):39－41.

［2］Feng C M，Chang C.Optimal slot allocation with empty container reposition problem for Asia ocean carriers［J］.International Journal of Shipping and Transport Logistics，2010，2(1):22－43.

［3］Moon I K，Ngoc A D D，Hur Y S.Positioning empty containers among multiple ports with leasing and purchasing considerations［J］.OR Spectrum，2010，32(3):765 －786.

［4］Chou C C，Gou R H，Tsai C L，et al.Application of a mixed fuzzy decision making and optimization programming model to the empty container allocation［J］.Applied Soft Computing，2010，10(4):1071 －1079.

［5］Song D P，Dong J X.Effectiveness of an empty container repositioning policy with flexible destination ports［J］.Transport Policy，2011，18(1):92－101.

［6］段 刚，张 慧，陈 莉，等.铁路集装箱空箱调运问题的遗传算法［J］.铁道科学与工程学报，2011，8(3):110－115.

DUAN Gang，ZHANG Hui，CHEN Li，et al.Genetic algorithm for railway empty container allocation problem［J］.Journal of Railway Science and Engineering，2011，8(3):110－115.

［7］闫海峰，董守清.铁路集装箱结点站间空箱调配的优化［J］.中国铁道科学，2009，30(1):131－135.

YAN Hai-feng，DONG Shou-qing.Optimization of the empty containers distribution among railway network container freight stations［J］.China Railway Science，2009，30(1):131－135.

［8］朱德辉，何世伟.铁路罐式集装箱空箱调配优化模型及遗传模拟退火算法［J］.中国铁道科学，2008，29(6):104－110.

ZHU De-hui，HE Shi-wei.Optimization model of railway empty tank container allocation and genetic simulated annealing algorithm［J］.China Railway Science，2008，29(6):104－110.

［9］张得志，谢如鹤，黄孝章.铁路集装箱空箱调度模型及求解算法［J］.中国铁道科学，2003，24(3):125－129.

ZHANG De-zhi，XIE Ru-he，HUANG Xiao-zhang.Dispatch model and solution algorithm of railway empty container［J］.China Railway Science，2003，24(3):125 －129.

［10］彭 华，朱庆生.铁路集装箱空箱动态优化调度模型及求解算法［J］.交通与计算机，2007，25(5):38－41.

PENG Hua，ZHU Qing-sheng.Dynamic dispatch optimization model and solution algorithm of railway empty container［J］.Computer and Communications，2007，25(5):38－41.

Railway empty container allocation model based on cargo rank

DUAN Gang1，CHEN Li2，CHEN Zhi-zhong1，LI Yin-zhen1，LIU Yu-sheng2，YANG Xin-zhu3

(1.School of Traffic and Transportation，Lanzhou Jiaotong University，Lanzhou 730070，China;2.Department of Mathematics，Lanzhou City University，Lanzhou 730070，China;3.School of Mechatronic Engineering，Lanzhou Jiaotong University，Lanzhou 730070，China)

A nonlinear mixed integer programming on railway empty container allocation is modeled based on cargo rank according to railway transportation characteristic.The objective function is minimizing the cost of empty container allocation.Under short of empty container，the higher the cargo demand rank is，the more preferentially satisfied the empty container demand will be.A numerical case is given to demonstrate the validity and feasibility of the proposed model.

empty container allocation;cargo rank;mixed integer programming

U 292;U294

A

1672－7029(2011)04－0086－04

2011－06－30

国家自然科学基金资助项目(60870008);教育部新世纪优秀人才支持计划资助项目(NCET－10－0017)

段 刚(1977－)，男，吉林省吉林市人，讲师，博士研究生，从事交通运输系统分析研究