弧齿准双曲面齿轮啮合接触冲击有限元仿真分析＊*

姚启萍，唐进元

(1.高性能复杂制造国家重点实验室(中南大学)，湖南 长沙 410083;2.中南大学机电工程学院，湖南 长沙 410083)

螺旋锥齿轮啮合接触冲击是指齿轮副从静止到相对稳定啮合的过程中存在的冲击现象，在已有的关于螺旋锥齿轮动力学研究的文献中，可以发现研究者对螺旋锥齿轮传动的静态或准静态问题进行了大量的研究，并获得了较为成熟的结果［1－5］，针对冲击现象的研究不多，课题组对圆柱齿轮的啮合冲击行为进行了研究［6］。本文在CATIA中建立精确的螺旋锥齿轮副模型后，运用ABAQUS的显式动力学分析功能分析冲击过程中螺旋锥齿轮齿面接触力的变化情况，结果显示齿面接触力瞬时最大值比稳态值大近1倍，表明齿轮副的啮合冲击阶段不容忽视，有必要深入研究。

螺旋锥齿轮啮合接触冲击问题是一个边界条件高度非线性的接触动力学问题，难以求得解析解。随着有限元方法和有限元分析软件的快速发展，以及近年来在非线性分析方面的成功应用，作者运用有限元分析软件对弧齿准双曲面齿轮啮合接触冲击问题进行研究，为进一步深入研究啮合冲击问题积累经验。

1 螺旋锥齿轮模型

1.1 几何模型

螺旋锥齿轮齿面几何形状复杂，本文采用VB6.0开发CATIA的螺旋锥齿轮CNC加工仿真系统［7］，该系统能仿真螺旋锥齿轮的加工过程，生成基于各种加工方法的几何模型。

使用的加工参数根据“局部共轭原理”［8］计算得到。通过局部共轭原理得到的齿轮副对安装误差的敏感性较低，应用效果更佳。

以一对采用HFT方法(大轮成形法，小轮刀倾法)加工的弧齿准双曲面齿轮为例分析其啮合接触冲击行为，根据表1－表3参数得到齿轮的几何模型如图1所示。

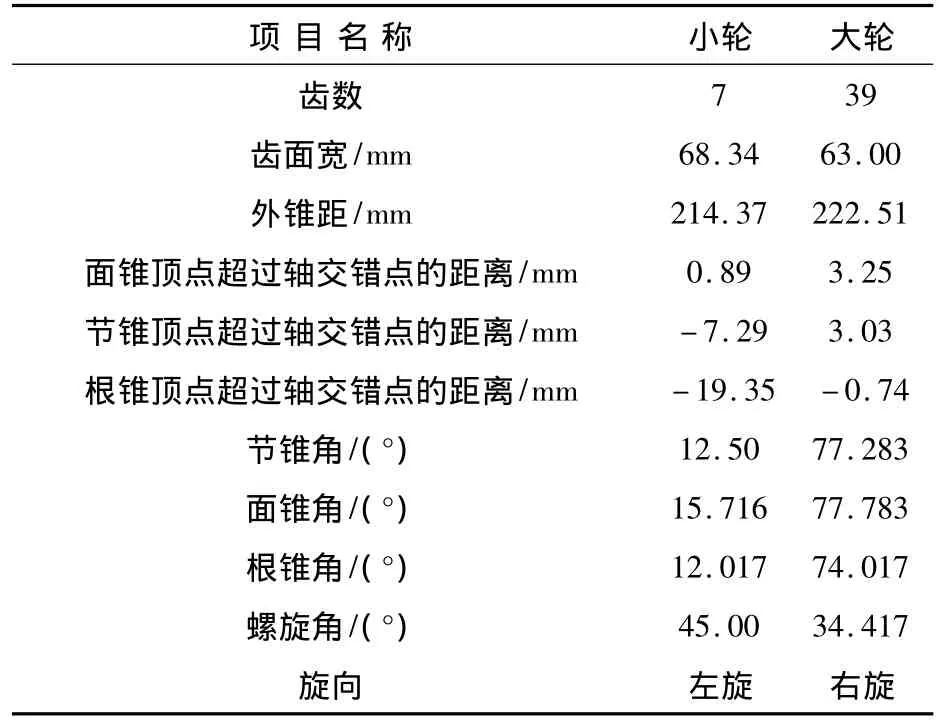
表1 齿轮几何参数Table 1 Geometric parameters of hypoid gear

表2 大轮的加工参数(Gleason No.609)Table 2 Machining parameters of the gear(Gleason No.609)

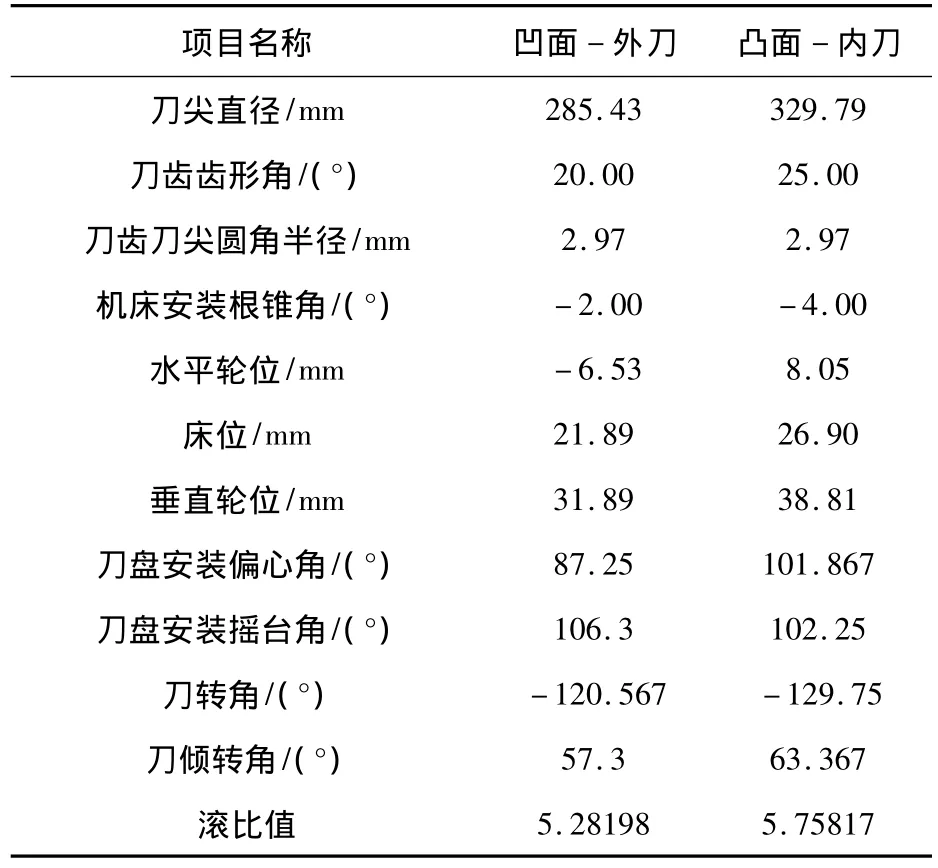
表3 小轮的加工参数(Gleason No.116)Table 3 Machining parameters of the pinion(Gleason No.116)

1.2 有限元模型

由于螺旋锥齿轮齿面在齿宽方向曲率较小，即齿面较扭曲，为了得到优质的网格，在考虑计算耗时和计算精度的前提下，在有限元前处理功能强大的Hypermesh软件中选用六面体线性减缩积分单元 (C3D8R)进行螺旋锥齿轮的网格划分。有限元的接触分析中，需要确定所选单元的有效性和精确性，一般会进行赫兹计算以验证。本文与相关文献［9］中使用相同的模型剖分和单元类型，从此文章的赫兹验算中可知，对于一次缩减积分单元，在一定的载荷和材料参数条件下，网格密度对计算结果影响大，所以本文在研究过程中细化齿轮副的网格，将ALLAE/ALLIE控制在1%以内，有效地控制了沙漏模式的扩展。齿轮的材料属性设置为:弹性模量为210 GPa，泊松比为0.3，密度为7800 kg/m3。

齿轮副的有限元模型如图2所示。

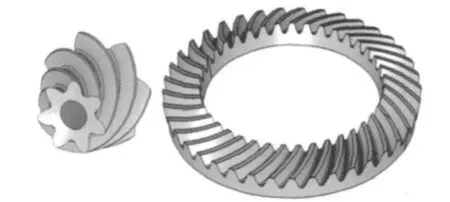
图1 准双曲面齿轮的几何模型Fig.1 Geometric model of hypoid gear

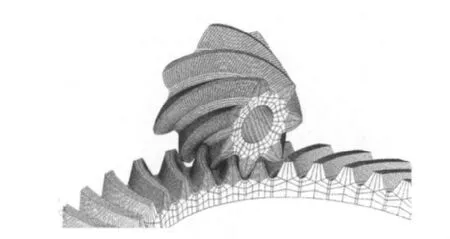
图2 齿轮副的网格模型Fig.2 Mesh model of gear pair

1.3 约束和边界条件

为了模拟齿轮副的实际安装、啮合情况，设定以下边界条件和约束:

(1)分别在大小轮的轴线上设定一个参考点，在参考点与相应齿轮内表面之间建立耦合约束，使齿轮内表面上受到的合力和合力矩与施加在参考点上的力和力矩等效，并允许在受载时，耦合约束面上的各部分之间可以发生相对变形;

(2)分别约束2个参考点除齿轮旋转方向以外的5个自由度;

(3)设定切向摩擦系数为0.15的5对大小轮齿面接触对;

(4)设定小轮的转速为500 rpm，大轮的扭矩为9×103N·m。

2 齿轮啮合接触冲击分析

在有限元的计算求解方法中，有2个大的类别，隐式求解与显式求解，其各有不同的特点。在此，选择 ABAQUS/Explicit作为分析平台。ABAQUS/Explicit可以进行显示的动态分析，结合论文提出的问题，使用中心差分法结合罚函数法的显式求解方式。

显式中心差分法在求解过程中，利用递推公式求解运动方程不需要进行矩阵的求逆，这对求解非线性问题有很重要的意义。因为在求解非线性问题时，每个增量步的刚度矩阵是被修改的。使用显式算法，避免了矩阵求逆的运算，大幅减小了计算量，而且没有迭代误差。同时，ABAQUS/Explicit利用罚函数法将附加约束条件引入泛函以进行求解，而没有使用拉格朗日乘子法。因为使用罚函数法不会增加问题的自由度，而且能使求解方程的系数矩阵保持正定，可以很好地与动力学中的显式积分求解方法相协调。

3 啮合接触冲击分析结果

完成有限元模型的建立之后，求解任务。完成分析后，进行结果处理。

如图3～4所示，瞬时接触区呈椭圆，接触区内的单元所受接触力大，并向外逐渐减小，这与滚动检验的结果吻合。

图3 大轮凸面接触压强的云图Fig.3 The contact pressure cloud of the gear convexity

图4 小轮凹面接触压强的云图Fig.4 The contact pressure cloud of the pinion concavity

图5 大轮凸面等效应力云图Fig.5 The mises stress cloud of the gear convexity

图6 小轮凹面等效应力云图Fig.6 The mises stress cloud of the pinion concavity

图7 John Argyris得出的有效接触应力云图Fig.7 The mises stress cloud of the gear analysed by John Argyris

如图5～6所示，齿面的等效应力并不只出现在接触区内，而是沿着接触区向齿根和齿顶蔓延。等效应力基于畸变能提出，用于说明单元体在复杂应力状态下的综合受力，判断其接近屈服极限的趋势。所以从图示分析结果可知，齿轮非接触区虽未直接参与啮合接触而承受接触力，但是仍然受等效应力作用，说明其也可能在传动中因较大的有效应力而屈服失效。在其他使用有限元方法分析螺旋锥齿轮传动性能的文献中可以看到类似的结果［10］，如图7所示。此外，观察等效应力在整个分析过程中的变化发现，在一个齿面的完整啮合过程中，齿轮工作面上的等效应力作用区域沿着接触轨迹移动。表明在齿轮的传动过程中，齿面任一点受到周期的应力作用，最终可能导致齿轮的接触区齿面疲劳破坏，该仿真结论也与实际的情况吻合。

图8所示为同时进入啮合的轮齿对的总接触力随时间的变化情况，可见，在啮合初始阶段，总接触力迅速增大到80 kN，之后总接触力波动平缓并最终接近40 kN。表明，螺旋锥齿轮的设计要充分考虑啮合冲击产生的接触力。文献［11］研究了一对螺旋锥齿轮动态啮合性能时发现，齿轮从静止到稳定啮合工作阶段，存在一个明显的初始冲击，冲击造成的齿面接触力波动值较稳定的值大近1倍左右，如图9。

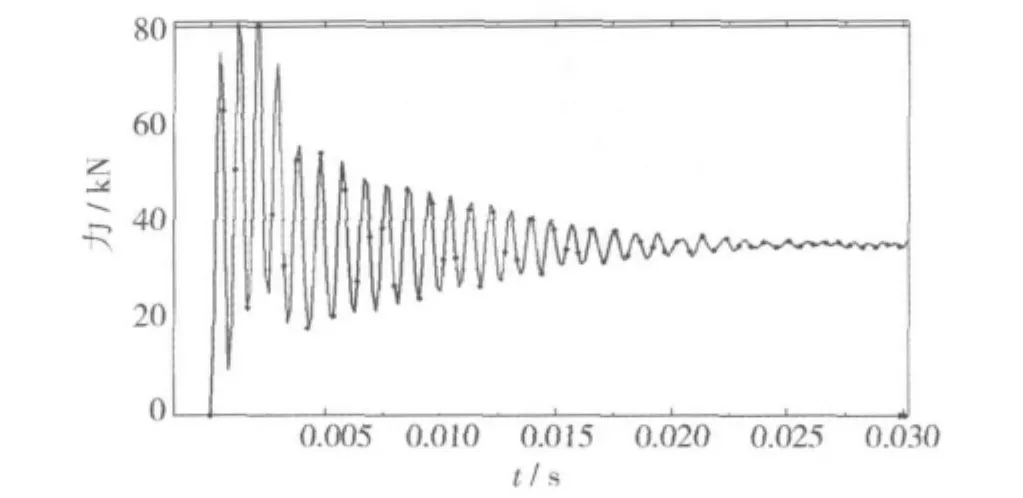
图8 齿面接触合力的变化曲线Fig.8 The resultant contact force of the tooth time history

图9 齿面接触力变化曲线Fig.9 The tooth contact force time history

图10 进入啮合的三对齿的接触力曲线Fig.10 The contact force of the three successive meshing teeth time history

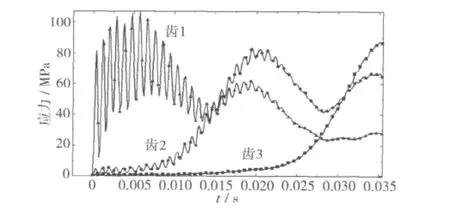
图11 进入啮合的三对齿齿根弯曲应力Fig.11 The bending stress of the three successive meshing teeth time history

在进入啮合的3对轮齿的接触力随时间变化的图中(图10)，第1对轮齿的接触力波动很大，第2对轮齿的波动较平缓且越接近啮出位置波动越小，第3对轮齿的接触力波动更小。结果表明，啮合冲击只对第1对轮齿有较大影响，且影响时间很短。

在此冲击过程中齿根弯曲应力的变化如图11，可以看出螺旋锥齿轮在发生冲击时对于齿根弯曲应力的数值影响并不大，但是对受到冲击的第1个齿的齿根应力造成剧烈波动。

4 结论

(1)在齿轮啮合过程中，接触斑点呈椭圆状且沿接触轨迹移动，齿面接触区上任一点在此过程中受到周期性的应力作用，最终可能导致在接触区内的齿面部分疲劳破坏;

(2)在啮合冲击过程中，轮齿对总的接触力波动衰减，最后趋于稳定值，在这个过程中，最大的瞬时峰值接近稳定值的2倍;

(3)在啮合冲击过程中，对单对轮齿来说，只有第一对轮齿的接触力峰值是稳定值的2倍左右，波动幅度大，频率高，但是冲击对第2对、第3对轮齿的影响较微弱;

(4)啮合冲击对进入啮合的第1对轮齿的齿根弯曲应力造成剧烈波动，但对峰值的影响较微。

［1］Wilcox L，Nowell G.Improved finite element model for calculating stress in bevel and hypoid gear teeth［C］//AGMA，97FTM5，Nov.1997.

［2］李盛鹏，方宗德.弧齿锥齿轮齿根弯曲应力分析［J］.航空动力学报，2007，22(5):843 －848.LI Sheng-peng，FANG Zong-de，Analysis of tooth root bending stress for spiral bevel gears［J］.Journal of Aerospace Power，2007，22(5):843 －848.

［3］张金良，方宗德.弧齿锥齿轮齿面接触应力分析［J］.机械科学与技术，2007，26(10):1268 －1272.ZHANG Jin-liang，FANG Zong-de.Analysis of a spiral bevel gear’s tooth contact stress［J］.Mechanical Scienceand Technology for Aerospace Engineering，2007，26(10):1268－1272.

［4］Argyris John，Fuentes Alfonso，Litvin F L.Computerized integrated approach for design and stress analysis of spiral bevel gears［J］.Computer Methods Applied in Mechanics and Engineering，2002(191):1057－1095.

［5］Litvin F L，Vecchiato Danniele.Computerized developments in design，generation，simulation of meshing，and stress analysis of gear drives［J］.Meccanica，40(3):291－324.

［6］唐进元，周 炜，陈思雨.齿轮传动啮合接触冲击分析［J］.机械工程学报，2011，7(47):22 －30.TANG Jin-yuan，ZHOU Wei，CHEN Si-yu.Contact －impact analysis of gear transmission system［J］.Journal of Mechanical Engineering，2011，7(47):22 －30.

［7］唐进元，蒲太平，颜海燕.螺旋锥齿轮双重双面法多轴联动数控加工计算机仿真研究［J］.制造技术与机床，2008(2):25－29.TANG Jin-yuan，PU Tai-ping，YAN Hai-yan.Research on simulation system of duplex spread blade multi－axis machining for spiral bevel gears［J］.Manufacturing Technology ＆ Machine Tool，2008(2):25 －29.

［8］曾 韬.螺旋锥齿轮设计与加工［M］.哈尔滨:哈尔滨工业大学出版社，1989.ZENG Tao.Spiral bevel gear design and manufacturing［M］.Harbin:Harbin Institute of Technology Press，1989.

［9］唐进元，蒲太平.加载螺旋锥齿轮接触轨迹变化规律的研究［J］.机械科学与技术，2010，4(29):461 －466.TANG Jin-yuan，PU Tai-ping.A study of contact path variation of a loaded spiral bevel gear［J］.Mechanical Science and Technology forAerospace Engineering，2010，4(29):461 －466.

［10］Argyris John，Fuentes Alfonso，Litvin Faydor L.Computerized integrated approach for design and stress analysis of spiral bevel gears［J］.Computer Methods in Applied Mechanics and Engineering，2002(191):1057 －1095.

［11］唐进元，彭方进.准双曲面齿轮动态啮合性能的有限元分析研究［J］.振动与冲击，2011，7(30):101－106.TANG Jin-yuan，PENG Fang-jin，Finite element analysis for dynamic meshing of a pair of hypoid gears［J］.Journal of Vibration and Shock，2011，7(30):101 －106.