基于时间窗的城市医药品动态配送路径优化模型与算法＊*

郑国华，周小强，张力敏

(1.中南大学交通运输工程学院，湖南 长沙 410075;2.湖南三一工业职业技术学院，湖南 长沙 410129)

1 问题的提出

在城市医药品配送网络体系中，由于区域内医药供应链终端客户需求信息的不确定性，导致医药物流配送中心的配送路径动态变化。如何在客户需求的服务时间内，提供及时准确且成本最小化的配送服务，需要对城市医药品动态配送路径进行优化。

城市医药品动态配送路径优化问题少见专门研究，相关研究成果主要集中在一般性的动态车辆路径问题上［1］。Dror等［2］集中研究了动态随机车辆运输的需求建模方法，并将模型应用于邮政速递、产品配送和生产调度等众多领域;Hanshar等［3］研究了当客户的需求不确定或交通信息发生变化时，如何在满足相关约束的条件下为车辆寻求最合理的规划路径;李兵等［4］通过引入虚拟任务点的方法将其转化为一个静态的车辆路径问题，并采用节约算法求解;刘士新等［5］设计了在动态环境下进行车辆路径优化的导向局域搜索算法;Alan等［6－9］也从不同的角度对动态车辆路径优化问题进行了相关研究。但上述文献研究极少考虑到时间窗因素，本文主要以客户服务时间窗为约束，以降低药品配送费用及提高服务准时性为目标，建立配送路径初始与动态优化模型，并设计了遗传算法［10］，对城市医药品动态配送路径优化问题进行相关研究。

2 问题分析及变量定义

医药品作为一种特殊的商品，不仅品类繁多、分类复杂，而且储运条件要求高、时效性强。针对医药品的独特性，在对城市医药品配送网络的路径优化建模时，摒弃了按零售端店面划分配送节点的传统做法，而是采用按零售端需求的医药品种来划分配送节点，以有效解决医药品配送时，由于品类多、分类杂而造成的分拣难度大的问题，亦可有效地满足医药品配送中客户多批次、小批量的配送服务需求。

为发挥规模经济性和技术经济性，假设某一城市区域内确定由一家医药配送中心对城市医药客户进行配送，且该医药配送中心总能满足医药客户的需求，其服务水平主要体现为在客户规定的时间窗范围内，最大化服务客户的数量和最小化配送服务的费用，其中药品配送费用主要考虑配送当中的运输费用。

首先，根据客户的初始订单进行配送路径的初始优化，配送车辆从医药配送中心出发将药品送到各客户点，然后返回医药配送中心，假定每个客户点的位置、需求量与服务时间已知，每辆车的载重量一定，要求合理安排配送路径，尽可能地降低配送费用及提高服务准时性。

其次，在初始配送路径优化的基础上结合动态需求信息进行城市医药品动态配送路径的优化。所谓动态需求信息主要有包括4种情形:①原客户需求量减少;②原客户取消订货;③原客户需求量增加;④新客户订货。

上述情形下的动态配送路径优化问题主要考虑以下状态:

(1)若动态需求信息只出现情形①或②，对于取消订货的原客户直接跳过到下一客户，初始配送路径不变。

(2)若动态需求信息出现情形③或④，则需建立相关模型进行配送路径的动态优化，此时，由于有些配送车辆已经驶离医药配送中心并且服务了部分客户，车辆的剩余载重量发生了改变，为此本文特引入虚拟配送中心的概念。若该时刻配送车辆位于某服务的客户点处，则将该客户点设为虚拟配送中心，否则将下一服务客户点设为虚拟配送中心，此时，将该时刻未服务的客户(虚拟配送中心除外)都作为新客户处理。因此配送路径动态优化问题可表述为:在客户需求信息实时更新的情况下，配送车辆从医药配送中心以及虚拟配送中心出发对新客户进行配送服务，然后返回医药配送中心，每辆车的载重量一定，要求合理优化配送路径以尽可能地降低配送费用及提高服务准时性。

为方便叙述起见，定义变量如下:

S'表示原配送中心;W表示配送车辆的载重量，且载重量相同;集合L={1，2，…，l}表示初始订货客户集合;gi(i∈L)表示每个客户的需求量;Tj表示到达客户j的时间;tij表示客户i到客户j行驶所用的时间;t'i表示服务客户i所需要的服务时间;LTj表示客户j要求的最迟到货时间;Pj表示药品不能按照客户j要求的时间段准时送达所产生的惩罚费用(货物提前到达不惩罚);集合L'={1，2，…，l'}表示新客户集合;g'i(i∈L')表示新客户的需求量;集合K={1，2，…，k}表示虚拟配送中心集合;W'k(k∈K)表示虚拟配送中心的剩余车载量;集合D={1，2，…，d}表示原配送中心可使用的车辆;Rik表示配送中心i的第k辆配送车的运行路径;Nik表示该路径上的客户数量;Nik=0表示未使用该车辆表示某客户在 Rik中的顺序号为j;Cij=t×α×S表示两点间的运输费用;α表示现实情况道路状况的修正系数，当道路状况拥挤时α＞1，当道路状况好时0＜α≤1;S表示两地的道路实际长度;t表示单位距离运输费用;β表示惩罚系数。

定义决策变量如下:

3 基于时间窗的城市医药品动态配送路径优化模型

3.1 基于时间窗的配送路径初始优化模型

以降低药品配送费用及提高服务准时性为目标，以客户服务时间窗、车载量为约束，建立配送路径初始优化模型如下:

目标函数(3－1)使得总的药品配送费用以及超出客户服务时间窗所产生的惩罚费用之和达到最小;约束条件(3－2)为每辆车所服务的客户的需求量小于车辆的载重量;约束条件(3－3)为每个客户有且只有一辆配送车进行配送服务;式(3－4)提供了惩罚函数中Tj的数学表达式;约束条件(3－5)表示保证行车路径上时间的顺序性。惩罚函数(3－6)为药品不能按照客户要求的时间段准时运到客户手中所产生的惩罚费用(货物提前到达不惩罚)。

3.2 基于时间窗的配送路径动态优化模型

以降低药品配送费用及提高服务准时性为目标，以客户服务时间窗、车载量为约束，建立配送路径动态优化模型如下:

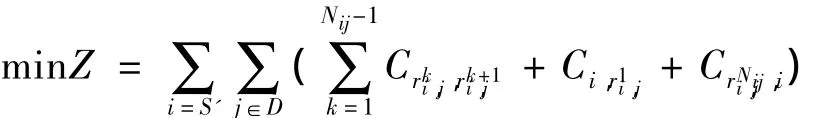
目标函数(3－7)使得总的药品配送费用以及超出客户服务时间窗所产生的惩罚费用之和达到最小;约束条件(3－8)限制从原配送中心出发所服务的客户的需求量不超过其车载量;约束条件(3－9)限制从虚拟配送中心出发的车所服务的客户的需求量不超过其剩余车载量;约束条件(3－10)、(3－11)、(3－12)限制每个客户点有且只有一个配送中心的一辆车提供服务;式(3－13)提供了惩罚函数中Tj的数学表达式;惩罚函数(3－14)为药品不能按照客户要求的时间段准时运到客户手中所产生的惩罚费用(货物提前到达不惩罚)。

4 遗传算法设计

城市医药品动态配送路径优化问题是一个典型的NP(Nondeterministic Polynomial)难问题，如采用传统方法对其进行求解，不但工作量大，花费时间长，而且通用性差，因此本文采用遗传算法(Genetic Algorithm，GA)求解。

4.1 染色体编码

采用符号来进行编码且基于贪婪构造法的方式进行译码，译码时只须按序尽最大可能地将基因位表示的客户点插入到路线中，当一个点违背时间窗或载重约束时，就开辟一条新路径并将这个点插入该路径。如编码为acdbfeghij，经过译码表示的路线为:路径1:0－a－c－d－0;路径2:0－b－f－e－g－0;路径3:0－h－i－j－0，其中0表示配送中心。

4.2 交叉概率、变异概率的自适应机制

在遗传算法中，对其收敛性起决定作用的是交叉和变异算子。在遗传算法中交叉概率一般取一个较大的数，变异概率一般取一个较小的数。为了避免发散和陷入局部最优点以及加快优化进程，本文提出新的自适应机制，通过个体适应度值间的比较，动态地调整pc和pm，对适应度值高的个体降低pm和pc，对适应度值低的个体提高pm和pc。

式中:fmax为种群中最大适应值;fmin为种群中最小适应值;f'为交叉个体的适应值;为种群的平均适应值;f为变异个体的适应值;pcmax为交叉概率的最大值;pcmin为交叉概率的最小值;pmmax为变异概率的最大值;pmmin为变异概率的最小值。

4.3 交叉、变异算子

交叉算子进行内部交叉，其操作方法如下:首先随机地在染色体串中选择一个交配区域，如父串交配区域选定为，然后将A的交配区域进行反转得到

变异算子采用随机交换染色体两点的基因值。

5 算例分析

设某医药配送中心为城市30位医药销售终端客户提供医药配送服务，配送中心在提供服务时，主要按零售客户需求的医药品种划分配送节点，其中18个客户对于品种A下了初始订单(考虑到其他医药品种的配送问题与品种A的配送问题一致，本文只针对医药品种A进行算例分析)，医药配送中心与各客户点间的实际距离、各客户的初始需求量以及客户的服务时间窗等初始数据不详细列出。

另设医药配送中心到各客户点的路况修正系数α =1.1，各客户点间的路况修正系数 α =1.2，单位距离运输费用t=2，其中α和t可以根据实际情况进行动态调整，惩罚系数β=0.5，每个客户点需要的服务时间t'=3，汽车的载重量相同且w=10。

首先根据客户的初始订货信息及配送路径初始优化模型，利用遗传算法求解得到城市医药品初始配送优化路径，遗传算法参数设置:种群个体数为30，迭代次数为300，pcmax=0.8，pcmin=0.6，pmmax=0.1，pmmin=0.005。考虑到通用启发式算法求取最优解的质量可能与初始解有关，而遗传算法又是从问题解的串集开始搜索，因此在上述算法的实现中，记录10次运算中得到的最优解目标值与初始解集平均目标值进行比较以此对前面所提出的优化模型和算法进行检验，结果如表1所示。可知最优解的目标值相对初始解集的平均目标值，其配送费用节省56.5% ～64.1%，由此可以证明配送路径初始优化模型及遗传算法的有效性，且算法可以迅速收敛到最优解，收敛曲线如图1所示。

表1 对应的初始解集平均目标值和最优解目标值Table 1 The average target of initial solution set and corresponding optimal target

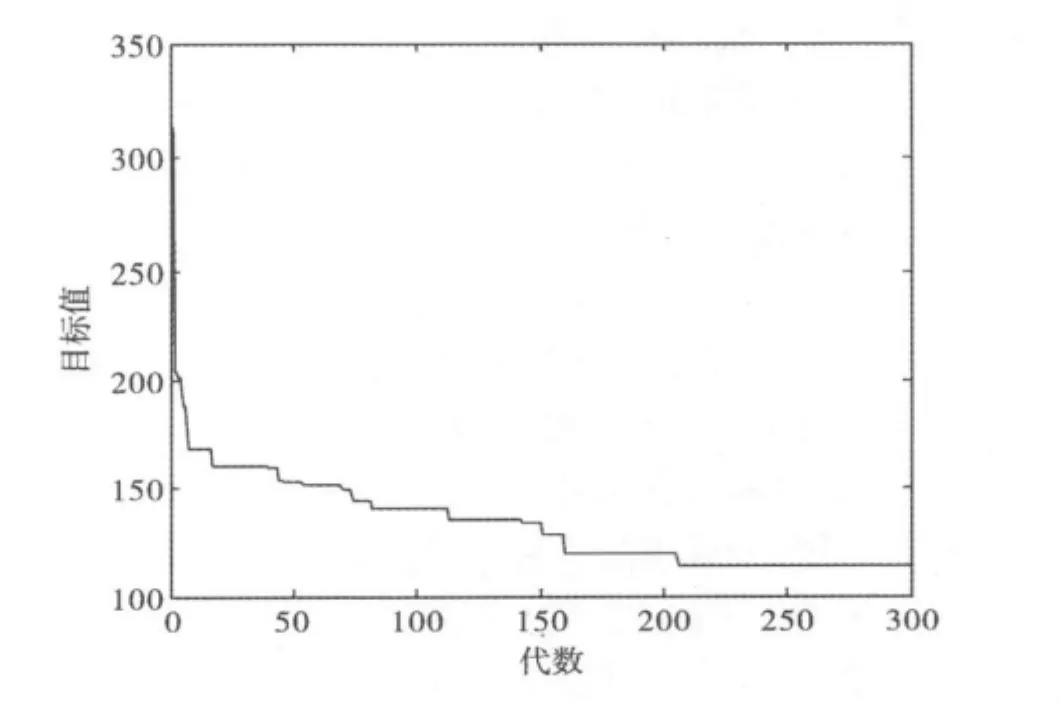
图1 初始配送路径优化收敛曲线图Fig.1 The convergence graph of initial distribution path optimization

将表1中最优解目标值最小的路径作为初始配送优化路径(见表2)。

表2 初始配送优化路径表Table 2 Initial distribution optimization path table

假设在时刻40更新客户动态需求信息，原客户6，17需求量分别增加 1，1，客户 25，23需求量分别减少2，1，此时又有5个新客户提出服务请求，其需求量及服务时间窗分别为32(2，［50，55］)，33(1，［52，58］)，34(2，［60，65］)，35(2，［65，70］)，36(2，［55，65］)，新客户到原配送中心与虚拟配送中心的距离等信息，这里不详细列出，此时需要进行配送路径的动态实时优化。

由初始优化配送路径信息可知，此时医药配送中心已发出4辆车，车辆1已经回到医药配送中心;车辆2服务完客户10，正在前往客户20的途中，因此客户20设为虚拟配送中心，剩余车载量为5;车辆3服务完客户17，在前往客户25的途中，因此客户25设为虚拟配送中心，剩余车载量为3;车辆4服务完客户23，在前往客户19的途中，因此客户19设为虚拟配送中心，剩余车载量为3;此时原配送中心依然服务，新客户数量总共为9个。

根据配送路径动态优化模型，利用遗传算法求解。遗传算法参数设置:种群个体数为30，迭代次数为300，pcmax=0.8，pcmin=0.6，pmmax=0.15，pmmin=0.005。同样考虑到通用启发式算法求取的最优解的质量可能与初始解有关，而遗传算法又是从问题解的串集开始搜索，因此在算法的实现中，记录10次运算中得到的最优解目标值与初始解集平均目标值进行比较以此对配送路径动态优化模型和算法进行检验，结果如表3所示。从表3可知，最优解的目标值非常接近，且相对初始解集平均目标值，最优解的目标值即配送总费用节省39.26% ～42.33%(由于此时问题的规模较小，因此配送费用节省较低)，算法能够迅速收敛到最优解，并且算例的计算时间为55 s，因此可以满足调度的实时性要求，动态配送优化路径如表4所示，算法的收敛曲线如图2所示。

表3 对应的初始解集平均目标值和最优解目标值Table 3 The average target of initial solution set and corresponding optimal target

表4 动态配送优化路径表Table 4 Dynamic distribution path table

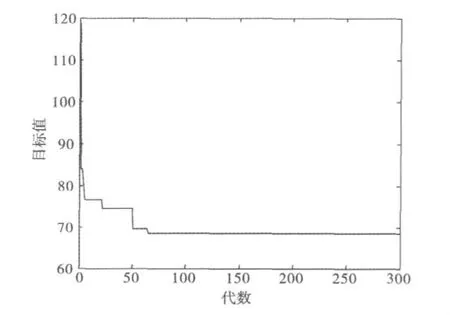
图2 动态配送路径优化收敛曲线图Fig.2 The convergence graph of dynamic distribution path optimization

6 结论

(1)考虑客户服务时间的要求，利用本文建立的配送路径初始优化模型、动态优化模型以及设计的遗传算法可以有效地优化配送路径，较大程度地节省配送费用，提高配送服务水平，并且满足城市医药品动态配送路径优化问题的实时性要求。

(2)本文所提出的优化模型和算法是解决城市医药品动态配送网络路径优化设计问题的一种有效方法，也可为其他需要考虑服务水平的物流配送网络路径优化设计提供较理想的决策支持。

［1］Psaraftis H N.Dynamic vehicle routing:status and prospects［J］.Annals of Operations Research，1995，61(1):143－164.

［2］Dror M，Powell W.Stochastic and dynamic models in transportation preface［J］.Operations Research ，1993，41(1):11－14.

［3］Hanshar F T，Ombuki－Berman B M.Dynamic vehicle routing using genetic algorithms［J］.Applied Intelli －gence，2007，27(1):89 －99.

［4］李 兵，郑四发，曹剑东，等.求解客户需求动态变化的车辆路径规划方法［J］.交通运输工程学报，2007，7(1):106－110.LI Bing，ZHENG Si-fa，CAO Jian-dong，et al.Method of solving vehicle routing problem with customers’dynamic requests［J］.Journal of Traffic and Transportation Engineering，2007，7(1):106 －110.

［5］刘士新，冯海兰.动态车辆路径问题的优化方法［J］.东北大学学报:自然科学版，2008，29(4):484－487.LIU Shi-xin，FENG Hai-lan.Optimization approach to solving dynamic vehicle routing problems［J］.Journal of Northeastern University:Natural Science，2008，29(4):484－487.

［6］Alan S.Specification for a dynamic vehicle routing and scheduling system［J］.International Journal of Transportation Management，2002，1(1):29 －40.

［7］熊 浩，胡列格.多车型动态车辆调度及其遗传算法［J］.系统工程，2009，27(10):21－24.XIONG Hao，HU Lie-ge.Dynamic vehicle routing problem with multiple vehicle type and its genetic algorithm［J］.Systems Engineering，2009，27(10):21 －24.

［8］吴兆福，董文永.求解动态车辆路径问题的演化蚁群算法［J］.武汉大学学报:理学版，2007，53(5):571－575.WU Zhao-fu，DONG Wen-yong.A mixed evolutionary ant algorithm for the dynamic vechicle routing problem［J］.J.Wuhan Univ:Nat.Sci.Ed.，2007，53(5):571 －575.

［9］吴 升，陈 楠.基于位置服务的动态车辆路径问题研究［J］.福州大学学报:自然科学版，2007，35(6):953－956.WU Sheng，CHEN Nan.Study on dynamic vehicle routing problem based on location － based services［J］.Journal of Fuzhou University:Natural Science，2007，35(6):953－956.

［10］周 明，孙树栋.遗传算法原理及应用［M］.北京:国防工业出版社，1999.ZHOU Ming，SUN Shu-dong.Genetic algorithms:theory and applications［M］.Bei Jing:National Defence Industry Press，1999.

［11］张得志，李双艳.不确定环境下协同运输优化模型及其算法［J］.铁道科学与工程学报，2010，7(4):116－120.ZHANG De-zhi，LI Shang-yan.An optimization model for coordination transportation and its solution algorithm under uncertain environment［J］.Jouranl of Railway Scinence and Engineering，2010，7(4):116 －120.