城市土地利用与多模式交通一体化模型＊*

江 航，胡列格，王 佳，陈舟宇

(1.长沙理工大学交通运输工程学院，湖南 长沙 410014;2.广西柳桂高速公路运营有限公司，广西 南宁 530028)

城市土地利用与交通的一体化规划是实现城市形态、土地利用与交通系统的互动反馈和相互协调的核心技术，对此，国内外学者作了多方面的研究。例如:著名的Garin－Lowry模型、Echenigue模型和日本的Calutas模型等是着眼于不同产业的选址行为，充分考虑不同产业间的相互作用，揭示土地利用和交通的关系［1－2］;王媛媛等［3］用城市交通系统的总出行时间作为城市土地利用的交通效率度量，从宏观上提出了基于交通效率的城市土地利用优化模型;YING［4］建立了土地利用和交通需求的组合模型，用灵敏度分析方法研究土地利用方案设计和交通政策的灵敏度;高自友等［5］将土地利用问题和城市交通网络设计问题相结合，提出了城市交通网络设计和土地利用问题的组合模型。然而，这些模型都是基于单一的交通模式，没有反映混合模式的交通系统对土地利用的影响，尤其是对城市土地利用形态有着导向和促进作用的公共交通没有考虑在内。

因此，为适应我国城市道路混合交通的特点和TOD为原则的土地利用规划，本文提出了一个受多模式交通网络均衡约束的土地利用模型，用来寻找基于多模式交通网络的土地利用优化方案，希望能达到在一定的土地利用约束下使城市各节点居住数量增加量最大、交通系统的总阻抗最小。

1 多模式交通网络均衡配流问题

土地利用决定着交通需求的强度、分布和结构，进而决定了多模式交通网络的均衡状态，多模式交通网络的均衡状态又约束着土地利用强度。因此，需要先分析多模式交通网络的均衡配流问题。

多模式交通网络均衡配流，即交通方式分担与交通分配组合模型，能够克服传统规划方法中各阶段预测结果相容性差、收敛慢的缺点，能准确地反应和描述实际的交通需求［6－7］。本文使用的多模式交通网络均衡模型中，用户对交通方式的选择按Logit函数分离，使用某一种交通方式的用户对路径的选择满足UE原则。

1.1 多模式交通网络中用户出行的均衡分析

在多模式交通网络中，出行者首先对交通方式进行选择。出行者具体选择何种交通方式出行取决于出行者对不同交通方式出行费用的理解。出行费用除了受走行时间、票价和舒适性等可测量因素影响，还受个人喜好、随机拥挤等不确定因素影响。出行者对各种交通方式的理解出行费用可以如下函数描述:

由于出行者的理解出行费用是一个随机变量，因此出行者的方式选择实际上是一个概率问题，某种方式被选择的概率取决于这种方式的特性和估计误差的分布，当估计误差相互独立且服从Gumbel分布时，出行者对各种方式的选择比例满足Logit分离模型。即OD对rs间交通方式n被选择的概率为:

式中，θ为出行者对交通方式选择的随机性参数。

出行者选择完交通方式后，就需要对出行路径进行选择，用户对路径的选择满足以下原则:对选择每一种交通方式的出行者来说，在给定的OD对间，出行者所选择使用的各条路径上该方式的出行费用全部相等，并且小于或等于未被使用的路径上的该方式的出行费用。

假设OD对rs间出行者的出行需求为qrs，当多模式交通网络达到平衡状态时，出行者对交通方式的选择满足方式分担的Logit分离模型，选择每种交通方式出行的用户对路径的选择满足wardrop均衡。据此，可得出多模式交通网络的用户均衡条件:

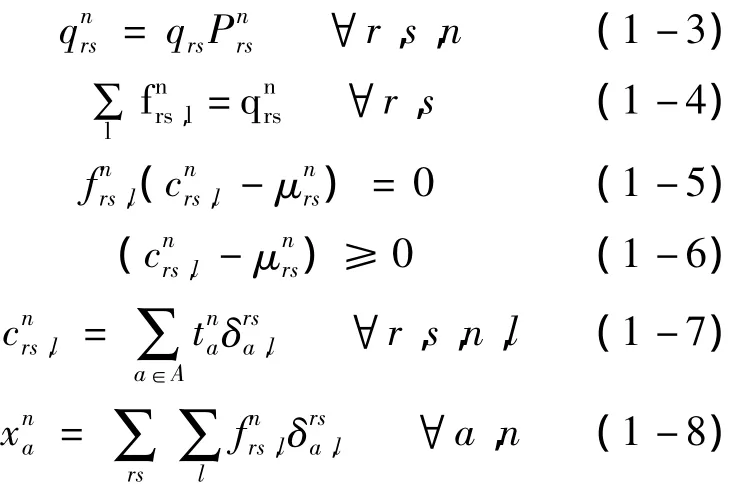
其中，式(1－3)表示出行者的方式选择满足Logit模型;式(1－4)表示某种交通方式的路径流量约束;式(1－5)和(1－6)表示选择某种交通方式出行的用户对路径的选择满足均衡原则;式(1－7)和(1－8)表示某种交通方式的路径费用和路段流量约束，表示网络中路段与路径之间的相关系数，若路段a在OD对rs间第l条路径上，取值为1，否则为0。

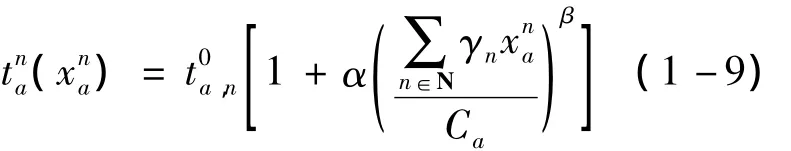
1.2 多模式交通网络平衡配流模型及算法

可以用如下的等价数学规划模型描述平衡状态下多模式交通网络的均衡配流:

此证明该模型的解满足多模式交通平衡分配的条件。

上述模型是在一组约束条件下的极小值问题，我们可以构造该模型的拉格朗日(Lagrangian)函数:

由式(1—11a)和(1—11c)可得交通需求在不同方式之间的分配关系满足Logit模型:

由式(1—11a)和(1—11c)可得对于每一种交通方式的流量分配满足用户平衡条件。

由此，可以得出以下结论:模型(1－10a)的解满足城市多模式交通网络均衡配流原则且解唯一。求解模型(1－10a)可用基于MSA的两阶段算法，见文献［9］。

2 土地利用与多模式交通网络一体化问题

2.1 一体化模型

本文使用双层规划描述多模式交通网络均衡制约下的土地利用问题。以土地使用的增加量为决策变量，以整个网络中的系统总阻抗与居住数量之差最小为目标，构建上层函数，表示处于上层的决策者的土地使用决策行为;下层函数使用多模式交通网络均衡配流模型，表示出行者根据上层函数中的决策，按照多模式交通网络均衡原则选择出行方式和路径。这种双层规划模型表述如下:双层规划模型P1(U1):上层问题

(L1):下层问题

在模型P1中，相关变量意义为:λr表示r小区人口增加量;λ是小区人口增加量的向量表示，作为上层模型的决策变量;ur表示r小区已知的居住数量;umax表示i小区所允许的最大居住数量;prs表示r小区中选择出行到s地区的人数比例;ξ表示居住数量与系统总阻抗单位匹配系数。

2.2 基于灵敏度分析的求解算法

在多模式交通网络均衡模型中包括2类变量:外部变量和内部变量。外部变量是事先给定的，如道路容量、自由流通行时间等;内部变量是由均衡模型计算出来的，如路段流量、各方式的出行量等。灵敏度分析就是将外部变量作为扰动参数，分析扰动参数的变化对均衡路段流量的影响。灵敏度分析的方法见文献［10－11］。

在本文设计的双层规划模型中，由于上层函数中的决策变量作为外部变量影响了多模式网络的均衡状态，多模式网络均衡状态又约束着上层决策函数，这种双层规划问题可使用灵敏度分析的方法求解。求解问题的基本思路如下:

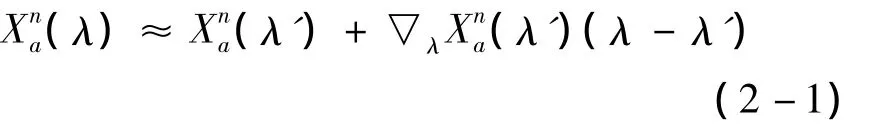
将式(2－1)代入上层模型中，则上层模型变为一个以土地利用变化为变量的普通非线性优化问题，可以求出最优解。将此最优解代入下层模型再次求解，可得到新的平衡路段流量，重复上述操作可得新的土地增加的分布值。如此重复计算，可得到满足收敛准则的上层规划问题最优解。

3 算例

本文采用文献［9－10］中的算例网络，如图1所示，网络中共有 A－D，A－F，E－F，E－D 4个OD对，7条路段，6个节点，其中A和E为居住区。网络中的土地利用情况如表1所示。

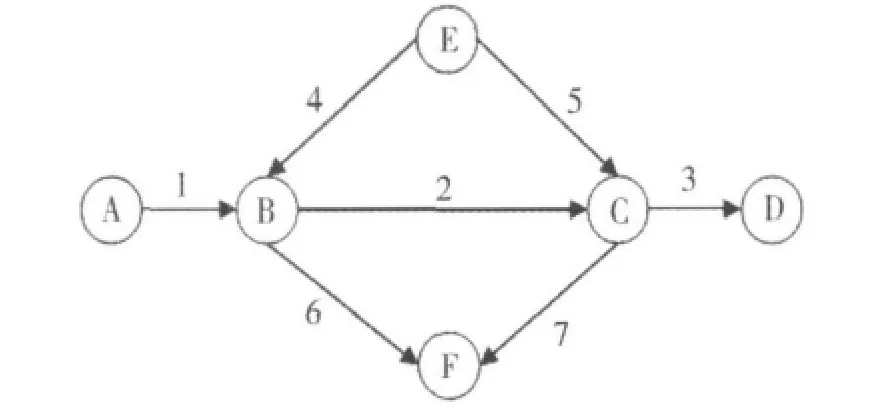
图1 算例网络图Fig.1 Demo traffic network

定义网络中存在2种交通方式，即小汽车(n=1)和公交车(n=2)，不同交通方式的吸引度为，式中和表示第n种出行方式在OD对rs之间的价格和方便性成本;m1和m2为参数，取值为m1=0.4，m2=0.1。2 种交通方式的特征如表2所示。

假定路网中各路段通行能力 Ca都为400 pcu/h，2种交通方式的路段旅行时间使用式(1－9)计算，取α =0.15，β =4.0，路段旅行时间函数的自由流时间如表3所示。

在计算土地利用和多模式交通网络一体化模型P1时，取迭代精度σ =0.001;初始土地使用的增加量λ0=0;由文献［5］知，ξ表示上层决策者对“系统最优”和“居住数量最大”2个目标重视程度的差异，ξ越大说明土地利用对多模式交通网络的影响越大，当ξ=0时表示不考虑土地利用问题，本文取ξ=0和ξ=30。经迭代计算后，得到A小区和E小区的土地利用增加量以及此时的路段均衡流量如表4所示。

计算结果表明，土地利用和多模式交通网络具有反馈关系，土地利用增加量作为决策变量，其变化会影响多模式交通网络的均衡状态。由于单位pcu的公交车载客量远大于小汽车，均衡时多模式交通网络可以容纳更多出行，因此上层函数的决策变量可以取得更大的数值。

表1 土地利用现状表Table 1 Land－use statement

表2 两种交通方式的特征Table 2 Characteristic of two travel modes

表3 路段上两种交通方式的零流时间Table 3 The free－flow link time of different mode in the test network

表4 模型计算结果Table 4 The result of the model

4 结论

(1)用双层规划模型可以反映我国城市道路混合交通系统与土地利用的动态反馈关系，基于灵敏度分析的求解算法可以有效求解该模型，得到最优土地利用方案，实现整个网络中的系统总阻抗与居住数量之差最小的目标。

(2)在下一步研究中，一是要研究新的上层目标函数，更多地考虑环境污染、投资预算等目标，同时要加入交通管理措施和土地利用形态等决策变量，以达到改善多模式交通网络的同时实现土地利用形态最优;另一方面要研究更符合实际的多模式交通网络均衡原则，例如考虑出行者换乘，路径选择中的随机因素和交叉口的转向延误因素。

［1］Boyce D E，Mattsson L G.Modeling residential location in relation to housing location and road tolls on congested urban highway networks［J］.Transportation Research B，1999 ，33(8):581－591.

［2］陆化普.交通规划理论前沿研究［M］.北京:清华大学出版社，2006.LU Hua-pu.Theoretical research frontiers in transportation planning［M］.Beijing:Tsinghua University Press，2006.

［3］王媛媛，陆化普.基于可持续发展的土地利用与交通结构组合模型［J］.清华大学学报:自然科学版，2001，44(9):1240－1243.WANG Yuan-yuan，LU Hua-pu.Integrated model of urban land－use and modal split based on sustainable development［J］.Journal of Tsinghua University(Science＆ Technology)，2001，44(9):1240－1243.

［4］YING Jiang－ qian.Continuous optimization method for integrated land use transport models［J］.Journal of Transportation Systems Engineering and Information Tech-nology，2007，7(6):64 －72.

［5］高自友，宋一凡，四兵锋.城市交通连续平衡网络设计——理论与方法［M］.北京:中国铁道出版社，2000.GAO Zi-you，SONG Yi-fan，SI Bing-feng.Urban transporatation continuous equilibrium network design problem:theory and method［M］.Beijing:China Railway Press，2000.

［6］Fisk C S，Boyce D E.Alternative variational inequality formulations of the network equilibrium－travel choice problem［J］.Transportation Science，1983，17(4):213－216.

［7］林义成，李夏苗，刘大鹏.基于Log istic增长的城市交通运输方式共生模型及演化机理［J］.铁道科学与工程，2009，6(6):91 －96.LIN Yi-cheng，LI Xia-miao，LIU Da-peng .Symbiotic model of urban transportationmode base on Logistic equation and its evolutionmechanism［J］.Journal of Railway Science and Engineering，2009，6(6):91 －96.

［8］四兵锋，赵小梅，孙壮志.城市混合交通网络系统优化模型及其算法［J］.中国公路学报，2008，21(1):77－82.SI Bing-feng，ZHAO Xiao-mei，SUN Zhuang-zhi.Optimization model and its algorithm for urban mixed traffic network system［J］.China Journal of Highway and Transport，2008，21(1):77 －82.

［9］四兵锋，杨小宝，高 亮，等.基于出行需求的城市多模式交通配流模型［J］.中国公路学报，2010，23(6):85－91.SI Bing-feng，YANG Xiao-bao，GAO Liang，et al.Urban multimodal traffic assignment model based on travel demand［J］.China Journal of Highway and Transport，2010，23(6):85 －91.

［10］Patriksson M，Rockafellar R T.Sensitivity analysis of aggregated variational inequality problems，with application to traffic equilibria［J］.Transportation Science:2003，37:56 －68.

［11］Stephen D C，David P W.Sensitivity analysis of the probitbased stochastic user equilibrium assignment model［J］.Transportation Research Part B ，2002 ，36(7):617－635.