防洪物资调运的数学模型

汪 军, 孙志红, 刘信斌

(徐州空军学院基础部,江苏徐州 221000)

防洪物资调运的数学模型

汪 军, 孙志红, 刘信斌

(徐州空军学院基础部,江苏徐州 221000)

首先构建防洪物资调运的交通网络矩阵模型,并利用Dijkstra算法寻找各调运节点之间的最优路线,然后在平时以追求最小总调运费用、紧急情况下以追求最快调运速度为目标建立了防洪物资调运的优化模型,在此过程中引入偏离控制量以便充分考虑各调运节点的需求,讨论了调运期、偏离控制量对调运费用的影响,为科学制定调运方案提供依据,较好地解决了防洪物资的调运问题.

物资调运;Dijkstra算法;偏离控制量;调运节点

1 问题背景及重述

2007年5月江苏省工业与应用数学学会及中国矿业大学联合主办了第四届苏北数学建模联赛,联赛得到包括武汉大学、国防科技大学、中国农业大学等跨及全国12个省市60多所高校的积极参与,本文诣在解决其中的C题——防洪物资调运问题.

2 模型假设

(i)高等级公路与普通级公路的调运速度是恒定且相等的;

(ii)各企业、物资仓库及国家级仓储库之间的物资可以通过公路运输互相调运且所有公路均可双向运输;

(iii)调运物资的运输车辆是充足的,即一旦确定调运方案,即刻可调运完毕;

(iv)调运节点指生产企业、物资仓库、国家储备库共13个,调运期系指开始实施调运的时间;

(v)只考虑运输费用,不考虑物资装卸、储存等其它费用.

3 变量及符号假设

ri——调运节点i调运后的库存量(百件)

xij——从调运节点i到调运节点j之间的物资调运量(百件)Mi——调运节点i的最大库存量(百件)

为了实现城市规划中各中心城区与边缘居住绿色分隔，要对当地的实际情况进行调查分析，并根据不同的地理环境，遵循景观生态学的原理与方法科学合理的布局，从而更好的保护耕地，有效提升耕地综合利用率。

fi——调运节点i的预测库存量(百件)

vi——生产企业i的产量(百件/天),i=1,2,3

ti——生产企业i在调运期的生产天数(天)

z——总调运费用(元)

4 问题分析

通过对问题的分析,该地区的公路交通网络数学模型应该是指包含42个顶点的赋权图.所谓合理的调运方案就是要在尽可能地满足各个调运节点需求的前提下,平时尽量使调运费用最小,而在紧急情况下应尽快地将防洪物资调运到各需求点,这些都需要去寻找各调运节点之间的最优路径,所以这是一个优化问题,可以考虑建立该问题的规划模型.

5 模型的建立及求解

1.交通网络模型

在该地区交通网络图中调运节点共有13个,包括企业三家、物资仓库八个、国家储备库两个,为表达方便,我们按企业1,企业2、企业3、物资仓库1、……、物资仓库8、国家储备库1、国家储备库2的顺序编号为1到13,防洪物资的调运只限于在13个节点之间进行调运,故需找到它们之间的最优调运路线,平时应以最少运输成本Wij(i,j=1,2,…,13)为优.这里寻找最优路线时我们用Dijkstra算法来解决.

2.问题2及问题3的模型建立及求解

问题2要求设计一个在重点保证国家级储备库的情况下的合理调运方案,为此设从调运节点i到调运节点j的调运量为xij(百件),xij≥0,i,j=1,2,…,13.则调运结束后各个调运节点的库存量为

为重点保证国家级储备库的库存,合理调运方案必须使国家级储备库的库存达到或者超过其预测值:ri≥fi,i=12,13.仓库1到仓库8的应尽量达到或超过预测库存,为此考虑用一个偏离控制量ε(ε＞0)来控制,即

根据调运计划及各企业生产能力,调运期至少应为8天,才能满足基本要求,若给定ε=0.05,通过Lingo求解得调运方案见表1.

表1 调运期为8天时的最优调运方案

按此方案调运的最低总运输费用为321680元.

对于问题3,在问题2中令T=20,可以计算求得新的调运方案,此时调运总费用为299763元, 20天后各个调运节点的库存情况如表2所示.

表2 20天后各个调运节点的库存

3.问题4的模型建立及求解

问题4要求解决汛期部分路段中断情况下的紧急调运问题,此时应该考虑速度尽可能快,而无须考虑运费.鉴于洪水导致路段中断,故应构建新的交通网络赋权图G(V,E′),其中每条边的权值为smn,E′为集合E中去除边○14○23,○11○25,○26○27,⑨○31的集合,利用Dijkstra算法计算各调运节点之间的最短路径Sij(i,j=1,2,…,13),在问题2中将目标函数修改为

以8天为调运期,在约束条件不变的情况下,得到最优调运方案如表3.

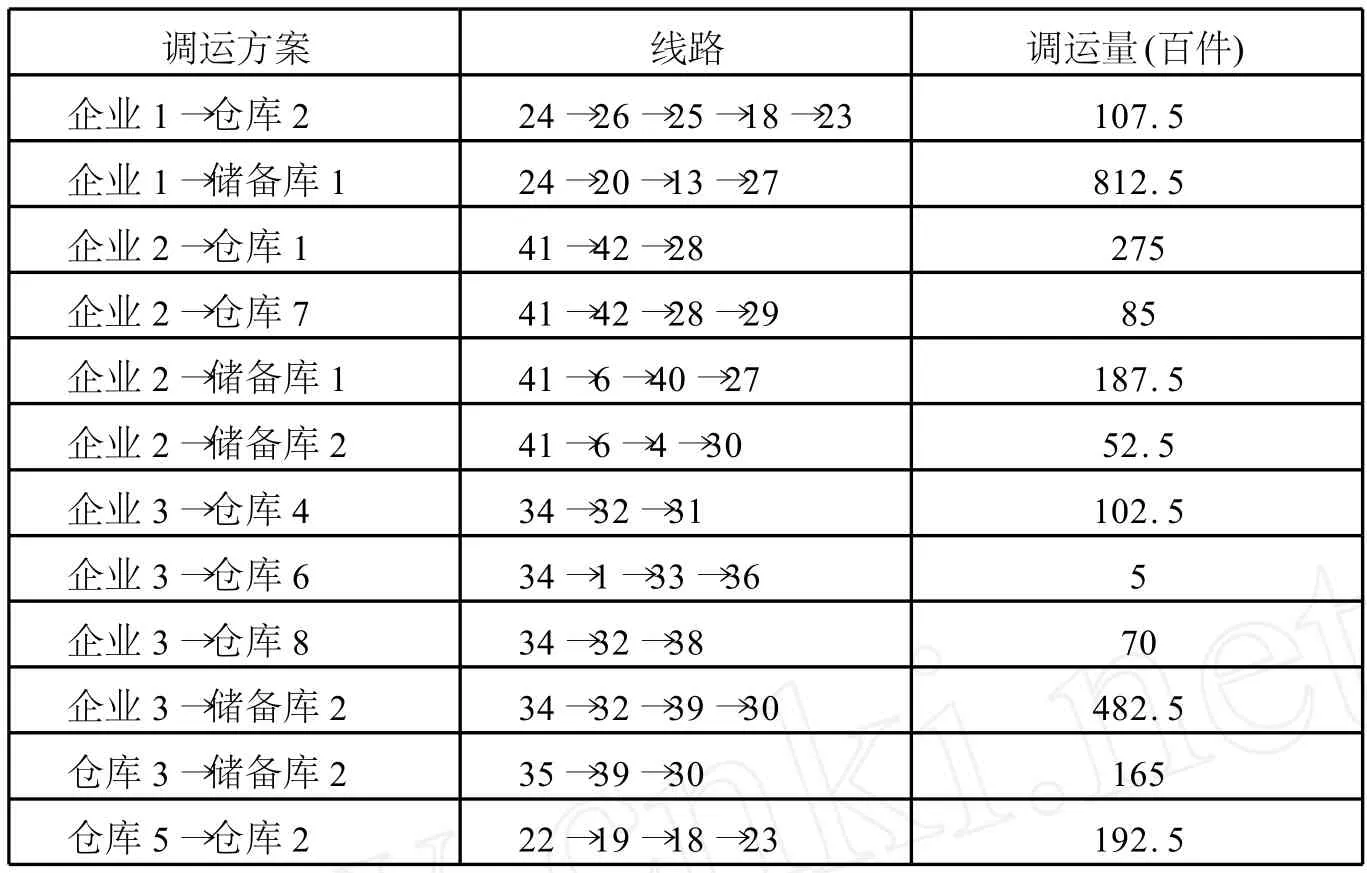
表3 调运期为8天时紧急情况下的最优调运方案

6 模型的进一步讨论

1.调运期的长短与运费的关系

在求解问题2和问题3的时候,我们发现,在调运期为8天的时候,总运费为321680元,调运期为20天的时候,总运费为299763元.显然,调运期的长短对最终运费有着显著影响.

我们希望能够找到一个最佳的时间,使得总运费能够达到最小,同时使各调运点的库存能够达到或超过预测值.为此对问题2中的模型进行修改,建立最佳时间模型如下.

在这个模型中,要求在调运完毕后,各库的库存都要达到或超过预测值.令T=8,9,10,…,计算得到调运期与总调运费用之间的关系如图1.

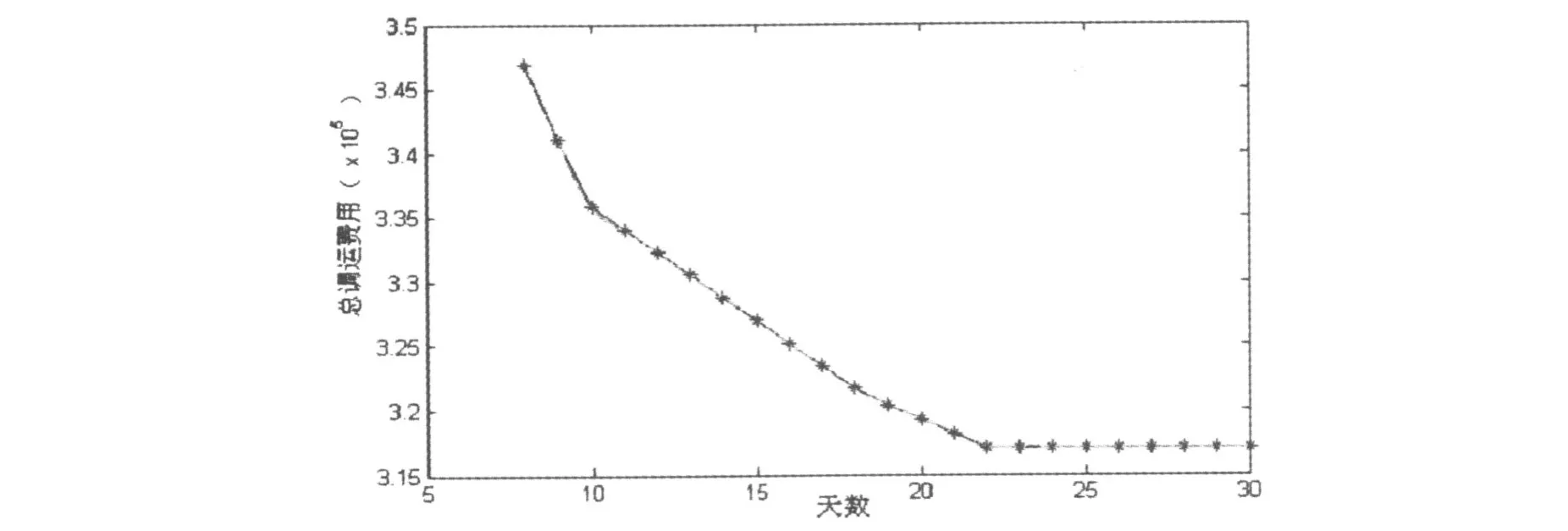
图1 调运期与总调运费用之间的关系

从图1可以看出,随着调运期的增加,总的调运费用不断下降.当T增加到22天的时候,调运费用趋于平衡,不再发生改变.造成这种情况的原因是,随着调运期限的增加,企业可用来生产的天数也增加,因而企业能够运出的物资量也增加,相应的输出选择面和灵活度也增加,从而使总运费降低.因此,根据此模型防汛部门可以科学制订调运期,特别是在准确预测汛期的情况下,对于提前做好科学决策有重要意义.

2.调运期的长短、ε的取值对费用的影响

ε的取值对于费用也有着重要的影响,我们希望能够找到ε和T对于总费用的影响效果.为此,在问题2的模型中,分别取不同的ε和T值从而得到总调运费用与ε及调运期T的关系如图2.

图2 总调运费用与ε及调运期T的关系

从图2可以看到,总调运费用均随着偏离控制量ε和物资生产天数T的增加而减少.这是非常符合实际情况的,因为ε的增大使得约束条件减弱,因而总的调运费用降低;物资调运期T的增加使得各个企业的产量增大,故导致调运任务的灵活性增加,因而总的调运费用降低.同时,从图2可以很明显地看出:ε波动对总调运费用的影响比物资调运期T的改变对总调运费用的影响要大.所以ε的控制效果是非常明显的.

[1] 汪军,等.战时航空油料的优化调拨[J].南京航空航天大学学报,1999,31(1):112-115.

[2] 姜启源,等.数学模型[M].北京:高等教育出版社,2004.

[3] 钱颂迪,等.运筹学[M].北京:清华大学出版社,1990.

[4] 袁新生,邵大宏,等.L INGO和Excel在数学建模中的应用[M].北京:科学出版社,2007.

[5] 谢金星薛毅.优化建模与L INGO/L INDO软件[M].北京:清华大学出版社,2004.

Mathematics M odel on Flood-Preven ting Material D ispatching

WANGJun,SUNZhi-hong,LIUXin-bin
(Foundation Department,Xuzhou Airforce College,Xuzhou 221000,China)

The dispatching netwo rk matrix modelwas constructed firstly,and the op timal dispatching routes between allocating and transporting points were seeked by virtue of Dijkstra algorithm.Furthermore,the optimal model of flood p revention material dispatching was constructed in pursuit of the fastest transferring speed in emergency.

In this p rocess,in o rder to fully consider the needsof all transport node,the deviate control variable was introduced, and the impact of the transpo rtation period,the deviate control variable on transpo rt costswere discussed,w hich p rovides the scientific basis fo r transferring p rogram,and give a better solution to flood-p reventing material dispatching p roblem.

material dispatching;Dijkstra algo rithm;deviate control variable;transport node

O221.1

B

1672-1454(2010)03-0137-05

2007-10-26