滑动效应对球轴承滚动体缺陷频率影响的研究*

侯新玉,范 君*,马俊杰,付献斌

(1.唐山海运职业学院 机电工程学院,河北 唐山 063509;2.河北环境工程学院 信息工程系,河北 秦皇岛 066102)

0 引 言

球轴承是旋转机械系统中重要的部件,对旋转机械系统起到承载作用,被广泛应用于航空航天、风力发电等领域[1-2]。同时,球轴承抗冲击能力较差,是机械设备中易损的零件之一。球轴承一旦发生故障,极有可能影响到整个设备的正常运行。因此,需要对球轴承进行故障监测,及时发现球轴承故障,从而保证设备的稳定运行[3-4]。

将轴承实际振动信号通过傅里叶变换得到的频谱,与求解轴承故障动力学模型得到的振动频谱进行对比,这是当前球轴承故障诊断的主要方法,国内外学者对此也进行了大量的研究[5-7]。

陈果[8]考虑了机匣的运动、支承刚度与油膜刚度等因素,分别建立了滚动轴承(含内圈、外圈、滚动体故障)的动力学模型,分析了系统的振动特征;同时,采用数值积分的方法,求解了中介轴承外圈早期剥落故障模型,获取了外圈故障激励作用下的整机振动,结果表明,中介轴承早期故障产生的冲击效应传递到机匣测点后发生了较大程度的衰减[9]。LIU J等人[10]认为滚动体与滚道间的接触为非赫兹接触,并认为滚动体经过缺陷-健康区域时,由于刚度变化而导致了接触力的变化,并研究了载荷、缺陷尺寸和类型对滚动体与滚道间接触的影响。

但上述对于故障轴承动力学响应的研究,并未考虑到弹流润滑作用下轴承内部存在的滑动效应。

对于轴承打滑的研究,国内外学者也开展了大量工作。

GAO S等人[11-12]采用建模与分析的方法,获取了轴承滚动打滑发生的条件,即当滚道与滚动体间的驱动力小于摩擦力时,滚动体将发生打滑。涂文兵等人[13-14]在考虑了转子系统启动阶段的加速工况的基础上,推导了轴承加速工况的动力学模型,获取了轴承加速阶段的滑动效应,该研究丰富了轴承打滑分析的相关理论;但其模型中并未考虑轴承的润滑条件,这使得模型计算结果与实际可能存在较大的误差。谢聪等人[15]考虑了滚道剥落引起的时变位移和时变冲击激励、油膜时变刚度和时变阻尼、钢球与滚道时变接触刚度和时变接触角、时变接触力等非线性因素,建立了外滚道剥落的高速轴承转子系统非线性动力学模型。袁倩倩等人[16]建立了考虑润滑碰撞的保持架动力学模型,研究了轴承保持架和滚动体之间的碰磨效应,得出了考虑润滑的保持架动态特性与试验更吻合的结论。韩勤锴等人[17]建立了一种角接触球轴承打滑预测模型,综合考虑了轴承部件间非线性接触与弹流润滑等因素,可以为建立弹流润滑作用下的球轴承动力学模型提供参考。涂文兵等人[18]考虑了轴承的时变刚度、游隙及打滑激励等因素,建立了滚动轴承滚动体打滑的动力学模型,可以为相关的研究提供参考。LI X等人[19]建立了球轴承在外滚道上存在故障的动力学模型,获取了球轴承接触角和载荷随转速的变化,可以为相关研究的创新点选取提供参考依据;但其研究对象为宽温域工况下的陶瓷轴承,对于钢制轴承而言是否适用尚未可知。牛蔺楷等人[20]建立了考虑轴承部件间相对滑动的滚动球轴承故障动力学模型,为球轴承的故障定性诊断提供了参考依据;但其并未准确量化滑动效应对球轴承缺陷频率的影响。

综合以往学者的研究,笔者拟建立一种考虑弹流润滑作用下球轴承滑动效应的轴承动力学模型;为获取含滚动体故障的轴承动力学响应,设置相应的滚动体缺陷,建立考虑轴承滑动效应的含滚动体缺陷的轴承动力学模型;通过试验对其进行验证,探究弹流润滑作用下滑动效应对滚动体缺陷频率的影响,为弹流润滑作用下球轴承的定量、定性诊断提供参考依据。

1 含滚动体缺陷的轴承动力学模型

含滚动体故障的轴承模型如图1所示。

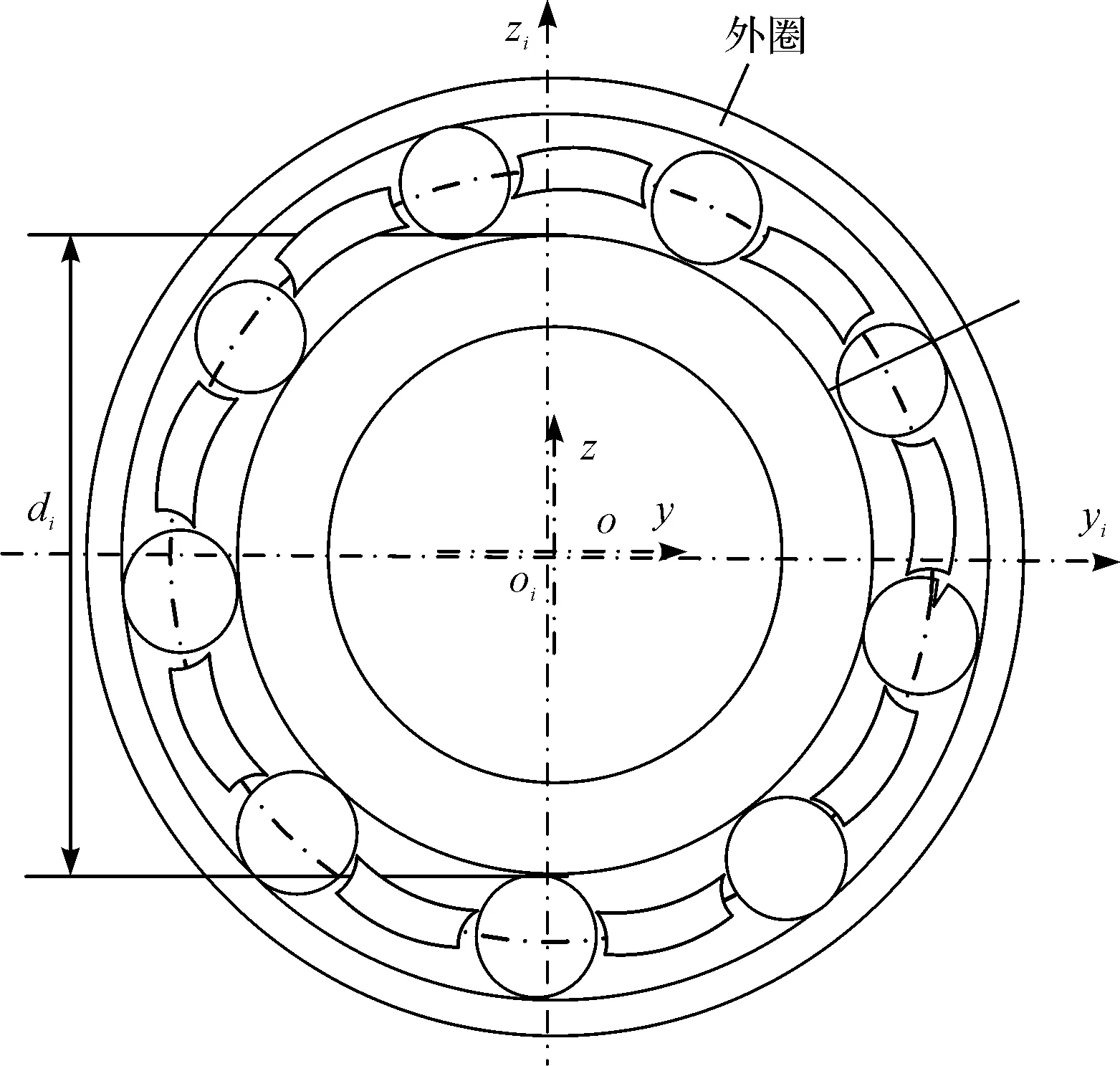
图1 含滚动体故障的轴承模型

第j个滚动体方位角ψj的表达式如下:

(1)

1.1 弹流润滑作用下轴承部件相互作用力分析

1.1.1 滚动体与部件的接触力与摩擦力

第j个滚动体与轴承各部件间的相互作用关系如图2所示。

图2 第j个滚动体受力示意图

设rj为第j个滚动体的径向位移,则第j个滚动体沿径向的变形可以表示为:

δij=[yicosψj+zisinψj-rj-0.5e-hi]+
δoj=[rj-yocosφj-zosinφj-0.5e-ho]+

(2)

式中:e为游隙;hi,ho为油膜厚度;“+”为等式只取正值。

根据赫兹接触理论,滚动体与内外圈间接触力为:

(3)

式中:KEi,KEo为润滑条件下滚动体与内外圈间的等效接触刚度。

滚动体与保持架间的接触力可以表示为:

(4)

式中:KEc为润滑条件下滚动体与保持架间的等效接触刚度;Vcj为接触点相对速度;θc为保持架转动角度。

充分润滑条件下,轴承滚动体与内圈、外圈、保持架间的卷吸速度可以表示为:

(5)

考虑卷吸速度的油膜厚度可以表示为:

(6)

式中:Eeff为弹性模量;ηo为润滑油黏度;N为接触力;α为黏压系数;u为卷吸速度;Ry为卷吸速度方向曲率半径。

对油膜厚度求偏导,可得到轴承滚动体与内圈、外圈、保持架间接触区的正向油膜刚度为Khi,Kho,Khc。

润滑入口区油膜刚度以及油膜阻尼可以表示为:

(7)

(8)

未考虑润滑时,刚度求解方法可由赫兹接触理论直接得出;而考虑润滑条件时,轴承部件间等效接触刚度为与干摩擦状态下的接触刚度与油膜刚度相关的等式。

因此,滚动体与内圈间的等效接触刚度可以表示为[21]:

(9)

式中:Ki为干摩擦状态下滚动体与内圈间的接触刚度。

KEo,KEc均通过该方法计算得到。等效阻尼的求解方法与等效刚度求解方法一致[21]。

滚动体与内圈间的摩擦力可以表示为:

Fij=μrNij

(10)

式中:μ为摩擦系数。

Foj,Fcj计算方式与此相似。

滚动体与保持架、内外圈间的摩擦系数可以表示为:

μc=(-0.1+22.28s)e-181.46s+0.1

(11)

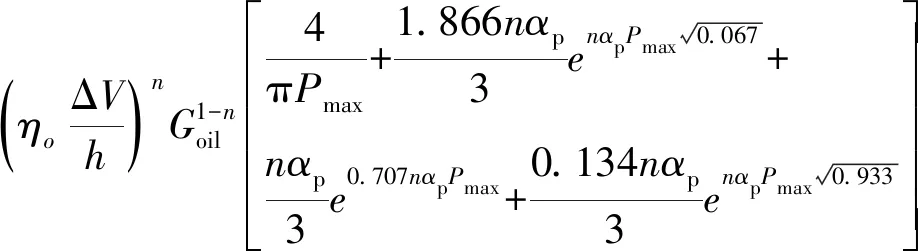
(12)

式中:s为滑滚比。

滚动体与内外圈间的滑移速度Vij,ΔVoj可以表示为:

(13)

滚动体上黏性阻力Fη可以表示为:

(14)

式中:ρe为油气混合物的密度;Cd是滚动体的阻力系数。

作用在保持架非引导面上的流体阻力Mc可以表达如下:

(15)

式中:Cb为保持架的阻力矩系数;Ac为保持架柱面面积。

1.1.2 故障激励

缺陷滚动体与内外圈接触的示意图如图3所示。

图3 滚动体缺陷与内外圈接触

滚动体缺陷与内、外圈接触时的撞击力Fpij、Fpoj可以表示为:

(16)

式中:ωm为滚动体公转角速度;mj为滚动体质量。

当滚动体故障点与内外圈接触时,各角度之间的关系可以表示为:

(17)

定义α、β为滚动体缺陷与轴承内、外圈的开关量,其可以表示0为:

(18)

式中:ωr为滚动体自转角速度;ni,no为滚动体缺陷分别与内外圈接触时转过的圈数。

ni,no可以表示为:

(19)

1.2 动力学模型的建立

含滚动体缺陷故障的轴承内外圈的动力学方程可以表示为:

(20)

(21)

式中:Nij,Noj为第j个滚动体与内、外圈的接触力;FRij,FRoj为第j个滚动体与内、外圈的摩擦力;Frij,Fpoj为缺陷滚动体与内、外圈接触时产生的故障激励;Fe为不平衡质量引起的偏心力;φj的计算方法与ψj一致。

保持架的运动可以描述为:

(22)

式中:Ncj为保持架与滚动体间的接触力;Jc为保持架的转动惯量。

保持架转速ωc可以表示为:

(23)

如图2所示,滚动体与保持架间的接触力为Ncj,其滚动体动力学方程可以表示为:

(24)

2 仿真计算

仿真计算以深沟球轴承为研究对象,选用的轴承型号为SKF公司生产的6205深沟球轴承,轴承接触角为0,系统所受轴向载荷为0。

6205深沟球轴承参数如表1所示。

表1 球轴承参数

考虑到轴承内外圈沟道曲率,此处内圈滚道直径为30.6 mm,外圈滚道直径为46.3 mm,轴承内圈所受不平衡质量为0.5 g,其他结构质量参数可由相关物理公式得出。

润滑剂为润滑脂,密度为850 kg/m3,常温时的动力黏度为0.04 Pa·s,极限剪切系数为0.043 4,黏温系数为0.027,黏压指数为Z=0.45。

内圈转速设定为2 400 r/min,径向载荷设置为500 N。

该轴承中只有一个滚动体含缺陷故障,且缺陷尺寸设置为θsi=θso=1°。假设缺陷区域无润滑油填充,外圈运动坐标系xoyozo等效于内圈运动坐标系xiyizi。

不考虑轴承内部滑动效应的滚动体缺陷频率可表示为:

(25)

第j个滚动体与内圈、外圈间的滑移速度如图4所示。

图4 滚动体与内外圈间的滑移速度

图4中,CD段滚动体进入承载后,与内圈间产生接触,摩擦力驱动滚动体进行公转与自转运动,同时滚动体自身重力、所受载荷也是驱动滚动体加速的因素,使滚动体与内圈间的滑移速度减小;由于弹流润滑作用下,滚动体与轴承内圈间的滑动效应始终存在,因此,滚动体与内圈间的滑移速度降低到一定程度后便不再降低;滚动体进入非承载区某区域后,内圈提供给滚动体的驱动摩擦力不足以克服自身重力,滚动体与保持架间的摩擦力、滚动体与内圈的滑移速度变大,滑动效应加剧。

对于滚动体与外圈间的滑移速度而言,其承载区与内圈一致。当滚动体到达滚道顶端后,重力成为驱动滚动体加速的因素,轴承与外圈间的滑移速度快速降低;进入承载区后,在载荷的作用下,滚动体与外圈间的滑移速度趋于0;由于滚动体所受离心力始终朝向外圈,导致滚动体与外圈间的滑动效应始终大于内圈。

滚动体与内圈、外圈和保持架间的摩擦力曲线如图5所示。

图5 滚动体与轴承内圈、外圈、保持架间的摩擦力

滚动体进入承载区后,在载荷的作用下,其与内圈间的接触力增大,导致摩擦力增大;进入承载区后半段后,接触力减小,滚动体与内圈间的摩擦力减小,滚动体与保持架间摩擦力的变化趋势与此一致(外圈对滚动体的摩擦力对滚动体的运动起到了驱动或阻止的作用);滚动体进入承载区后,在重力与载荷的作用下,滚动体与外圈间的滑动效应降低,外圈对滚动体的运动起到驱动作用,滚动体转速迅速增大;当滚动体转速趋近理论值后不再加速,此时外圈对滚动体的运动起到了阻止作用,从而出现了如图5所示的摩擦力方向发生变化的情况。

滚动体在轴承内周期性运转,从而出现了摩擦力的周期性波动。

滚动体实际公转速度与理论公转速度的对比结果如图6所示。

图6 滚动体公转速度计算值与理论值的对比

由于滚动体与内圈、外圈、保持架间存在滑动效应,其与内圈、外圈、保持架间的摩擦力不断变化,滚动体的运动不再是纯滚动,其实际公转速度低于理论值,从而出现了如图6所示的结果。

笔者对含滚动体缺陷的轴承动力学模型求解,并对结果进行傅里叶变换,得到频谱如图7所示。

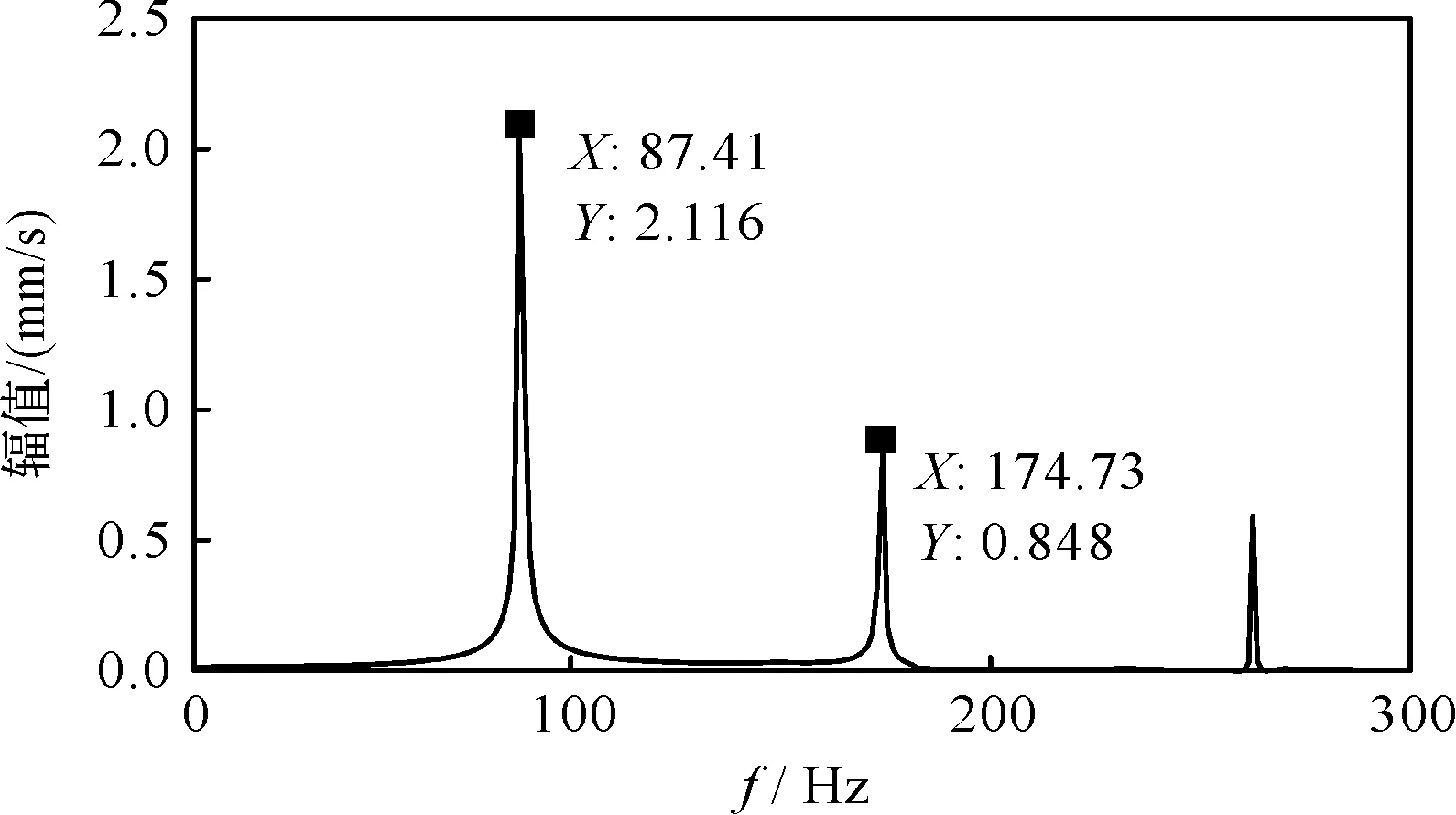
图7 考虑滑动效应的滚动体缺陷动力学模型频谱

笔者以fbsf,2fbsf表示滚动体缺陷特征频率,频谱中的主要频率为87.41 Hz、174.73 Hz,二者为滚动体缺陷特征频率及其倍频。

笔者根据式(25)求得滚动体缺陷特征频率约为93.40 Hz、186.80 Hz,实际缺陷频率约为理论值的93.59%,说明考虑滑动效应的滚动体缺陷频率小于理论值。这是由于考虑球轴承内部的滑动效应后,滚动体的实际公转速度小于理论值,表现出如图6所示的转动波动,以致含缺陷的滚动体周期性冲击轴承内外圈的时间间隔增大,使实际特征频率低于理论值。

笔者将径向载荷设置为1 000 N,求解其动力学模型,并将其结果与径向载荷为500 N的频率曲线对比,得到的频谱如图8所示。

图8 不同载荷下的特征频率曲线

频谱中的主要频率成分如表2所示。

表2 不同载荷下缺陷频率与理论值的对比

在图8与表2中,当载荷为1 000 N时,滚动体缺陷特征频率fbsf为90.17 Hz,二倍特征频率2fbsf为180.42 Hz,缺陷频率及其倍频与增大载荷前相比有所增大,但仍未达到理论值,滚动体缺陷频率约为理论值的96.54%。这是由于增大载荷后轴承内的滑动效应仍然存在,但增大载荷对轴承内的滑动效应有抑制作用,因而滚动体缺陷特征频率有所增大,但仍小于理论值。

上述结果与已有的研究成果是吻合的。

3 试验验证

为了验证弹流润滑作用下滑动效应对滚动体缺陷频率的影响,笔者专门搭建了轴承转子试验台,如图9所示。

图9 轴承转子试验台

其中,电机输出转速设置为2 400 r/min,且转速稳定,带动轴与轴承内圈转动,轴承润滑良好;含滚动体缺陷的轴承位于远离电机端,缺陷尺寸与仿真一致;采用加载器调节载荷,最大载荷1 200 N。

振动传感器采集轴承振动信号,采样频率1 024 Hz。由于轴承在实际运转中已存在滑动效应,因此设定载荷为500 N。

笔者将采集到的振动信号进行傅里叶变换,并将频率结果与理论值进行比较,以验证模型的正确性。最后得到了载荷500 N时的试验结果,即频谱如图10所示。

图10 载荷500 N时的试验结果

由于转子系统在运行过程中的非线性因素较多,频谱上出现了较多谐波频率分量。考虑87.06 Hz与174.10 Hz为滚动体缺陷频率和缺陷频率的二倍频,与理论值相比,Fr=500 N时的滚动体缺陷频率约为理论值的93.21%,发生了较明显的频率变化。这是由于轴承在实际运转过程中存在较明显的滑动效应,滚动体公转和自转速度均小于理论值,从而使滚动体缺陷频率低于理论值。

笔者设置Fr=1 000 N,转速不变,获取了相应的频谱,如图11所示。

图11 载荷1 000 N时的试验结果

由于增大载荷可以抑制轴承的滑动效应,89.97 Hz与179.81 Hz为此时滚动体缺陷频率和缺陷频率的二倍频,约为理论值的96.33%。与增大载荷前频率进行对比,可知缺陷频率发生了明显变化,但缺陷频率仍小于采用式(25)求得的理论值。

将试验结果与仿真结果进行对比,结果如表3所示。

表3 仿真结果与试验结果的对比

表3中,试验结果与仿真计算的结果偏差总体不超过0.4%,说明了该模型的正确性。

同时,也验证了滑动效应对滚动体缺陷频率存在较大的影响,在进行轴承故障诊断时,应充分考虑滑动效应带来的频率偏差。

4 结束语

在弹流润滑作用下,球轴承滑动效应引起的滚动体缺陷频率低于理论值,不利于球轴承故障诊断。为此,笔者综合以往学者的研究,建立了一种考虑弹流润滑作用下球轴承滑动效应的轴承动力学模型,研究了球轴承滑动效应对滚动体缺陷频率的影响;最后,通过试验对动力学模型的正确性进行了验证。

研究结论如下:

1)弹流润滑作用下,球轴承内存在明显的滑动效应,表现为滚动体的公转速度与自转速度低于理论值;

2)滚动体与外圈间的滑动效应更加明显,表现为在相同的角位置,滚动体与外圈间的滑移速度更大;

3)由于滚动体的公转与自转速度低于理论值,导致滚动体缺陷频率明显低于理论值。仿真与试验结果表明:500 N径向载荷下滚动体缺陷频率约为理论值的93%;增大载荷后,滚动体缺陷频率约为理论值的96%。该研究结果可为弹流润滑作用下球轴承的打滑抑制与故障诊断提供理论依据。

在后续的研究中,笔者将在该模型的基础上,考虑轴承运转引起的温升对润滑剂性能的影响,以进一步探讨轴承滑动效应对轴承故障特性的影响。