基于BPNN和MOOGA的高速联轴器多目标优化方法*
王艺琳,王维民,3*,李维博,王珈乐,张 帅
(1.北京化工大学 机电工程学院,北京 100029;2.北京化工大学 高端机械装备健康监控与自愈化北京市重点实验室,北京 100029;3.北京化工大学 高端压缩机及系统技术国家重点实验室,北京 100029)
0 引 言
随着工业场合对转子系统转速的要求越来越高,传统膜片联轴器已不能满足高速重载转子系统传递高扭矩、大转速及高容错的要求[1]。
超高速膜盘联轴器以其优越的性能,已被广泛应用于各类高速重载场合。近几十年来,汽车和航空工业的主要目标一直是减轻质量、提高速度、节约能源。为了缩短加工时间、节约制造能源,需要设计一款更精巧、转速更高、补偿性能更好的联轴器。
超高速转子系统利用挠性联轴器、依靠膜盘平稳地传递扭矩,以补偿联轴器安装制造过程中的平行和角向不对中。高转速联轴器工作时,承受大离心力、扭矩、平行和角向补偿等复杂载荷情况。如何在这类工况条件下,降低联轴器弯曲刚度,并减小其危险应力是目前联轴器多目标优化工作的重点。
长期以来,为提高联轴器的工作转速和优化其动力学性能,不少学者对膜盘联轴器进行了研究。
易源霖等人[2]基于轴复合刚度计算原理和Karush-Kuhn-Tucker最优化条件方法,计算了凸缘联轴器扭转刚度,发现了联轴器凸缘部分径向厚度和轴向长度对刚度的影响最大;但其并没有在研究的基础上提出结构的改进方案。李宽[3]采用有限元分析法和集中参数法,分析了转速和轴向伸缩量对联轴器轴向刚度的影响;但其没有对联轴器强度特性进行研究。曹安港等人[4]采用有限元仿真软件,分析了多种工况条件下联轴器应力分布情况;但其没有进一步研究联轴器设计参数对应力分布的影响。NAGESH S等人[5]采用有限元分析法,分析了高速挠性联轴器的动力学特性方程,并进行了试验验证;但其未研究复合工况下联轴器的动力学特性。马同玲等人[6]采用正交实验和数值计算的方法,研究了联轴器结构参数对其第三阶弯曲模态固有频率的影响,发现了柔性杆直径、电机端膜片斜度和发动机端膜片斜度对第三阶弯曲模态固有频率影响最大,并提出了一种结构优化方案;但其没有对该优化方案开展仿真实验验证。El-WAKEEL A等人[7]基于模糊逻辑、粒子群优化和单纯形方法,提出了一种混合模糊粒子群优化-单纯形算法,利用模糊粒子群优化-单纯形算法进行了联轴器结构参数优化,提高了联轴器扭转性能;但其未将该算法和其他优化算法进行比较,以说明该方法的优越性。于洋等人[8]基于联轴器扭转刚度性能,提出了一种优化联轴器设计方法,提高了柔性联轴器的使用寿命;但其没有研究复合工况下联轴器的弯曲刚度性能。于慧艳[9]采用ANSYS响应面优化方法,对联轴器强度进行了优化设计;但是其未综合考虑联轴器的强度特性和动力学特性。
随着联轴器设计转速的提高,单一优化目标不再满足要求,需要综合考虑联轴器强度和动力学特性。反向传播神经网络在工业领域的应用广泛,不少学者[10-12]利用反向传播神经网络结合遗传算法进行了机械构件的优化工作。
基于以上优化设计思路,笔者进行了联轴器多目标优化设计。
首先,针对传递转速达1×105r/min、补偿平行不对中0.1×10-3m、角向不对中0.25 °的超高速挠性联轴器强度及刚度优化问题,笔者通过正交实验和拉丁超立方抽样实验,对比多项式拟合法和反向传播神经网络法得到的联轴器结构参数与危险应力、弯曲刚度的目标函数,采用反向传播神经网络结合遗传算法对超高速膜盘联轴器的关键尺寸参数进行多目标优化,并对优化解集的可靠性进行验证。
1 基于神经网络拟合的多目标优化
1.1 关键参数选取
影响膜盘联轴器强度特性及动力学特性的参数众多,笔者采用多因素方差分析法筛选联轴器关键参数。多因素方差分析能够分析多个因素对应力与弯曲刚度的影响是否显著。
多因素方差分析的基本思路如下:
1)原假设。各个自变量不同水平下,总体均值无显著性差异,并且自变量各效应和交互作用为0;
2)计算检验统计量F值和显著性表征P值;
3)确定显著性水平值,给定显著性水平为0.15,比较各个自变量的显著性P值。若P大于0.15,则表示原假设正确,变量对总体均值无显著性差异;若P小于0.15则表征原假设错误,即变量对目标影响大,该因素对结果有显著性影响,可选为关键计算参数。
1.2 目标函数确定
为保证联轴器挠性足够小,并且降低应力,需要对联轴器进行多目标优化。采用遗传算法函数进行联轴器参数多目标优化时,需要能够准确反映参数性能的目标函数。目标函数的精确性越高,多目标优化的结果越可靠。目前常采用假定多项式法求解函数关系,多项式的项数越多,函数逼近的精度越高。
笔者采用二次多项式拟合三个关键参数与危险应力及弯曲刚度函数的关系,即:
(1)
(2)
式中:f为关键参数与危险应力函数;A1,A2,A3,A4,A5,A6,A7为f函数未知拟合系数;K为关键参数与弯曲刚度函数;B1,B2,B3,B4,B5,B6,B7为K函数未知拟合系数;x1,x2,x3为三个关键参数。
反向传播神经网络[13]擅长处理输入与输出因素间复杂的多元非线性关系。为避免训练之后的模型陷入过拟合状态,笔者采用贝叶斯正则化算法作为监督算法。
反向传播神经网络模型如图1所示。

图1 反向传播神经网络示意图
反向传播神经网络所采用的非线性激活函数为tansig函数,表示如下[14]:
(3)
式中:y为反向传播神经网络非线性激活函数;x为输入变量值。
笔者采用总误差准则函数作为评价指标,表示如下:
(4)
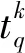
对比上文所述两种方法求得的目标函数可知,采用多项式方法的拟合精度较低,采用反向传播神经网络方法的拟合精度较高。
因此,笔者选取反向传播神经网络拟合目标函数进行多目标优化。
1.3 基于遗传算法的多目标优化方法
笔者利用多目标优化遗传算法函数对联轴器应力函数f、弯曲刚度函数K进行多目标优化计算。
相对单目标优化而言,多目标优化存在多个优化目标,而这些优化目标之间往往相互联系、制约甚至冲突。这意味着采用多目标优化不能得到某一组解,其得到的是一个Pareto解集[15-17]。
遗传算法通过模拟生物演化过程,对优化问题进行反复迭代,使得优化解集收敛且均匀分布,避免优化结果陷入局部优化状态,表示如下:
minF(x)={f1(x),f2(x),…,fm(x)}T
(5)
x={x1,x2,…,x3}T
(6)
xmin≤x≤xmax
(7)
式中:F(x)为多目标函数;x为设计变量;xmax为设计变量上限;xmin为设计变量下限。
2 联轴器参数优化
超高速挠性联轴器内外膜盘均采用焊接结构,内膜盘采用螺栓法兰与连接轴相连以传递转速,其结构如图2所示。

图2 联轴器示意图
联轴器内外膜盘均采用钛合金TC4材料,其材料特性如表1所示。

表1 钛合金TC4材料部分属性
2.1 联轴器仿真分析
笔者采用ANSYS有限元软件对联轴器进行仿真分析。各参数分别为:输入扭矩19.1 N·m,补偿平行不对中0.1×10-3m,补偿角向不对中量为0.25°。为方便后续开展参数优化工作,笔者直接利用ANSYS中自带的编辑模块进行联轴器参数化建模,利用Mesh模块生成六面体网格。
联轴器有限元模型如图3所示。
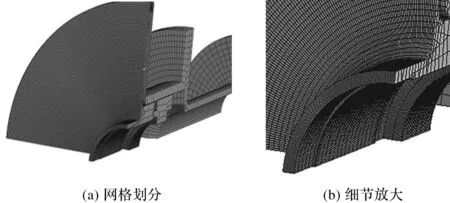
图3 联轴器有限元模型
联轴器的原设计转速6×104r/min,为满足超高转速转子系统要求,笔者将联轴器设计转速提高至1×105r/min,其余输入条件不变。
在设计转速6×104r/min时,联轴器的仿真结果如图4所示。

图4 6×104 r/min膜盘组应力情况
由图4可得:当转速为6×104r/min时,复合工况下膜盘联轴器最大应力集中在内膜盘根部,最大应力为194.46×106Pa。
转速提高至1×105r/min时,复合工况下联轴器的仿真结果如图5所示。

图5 1×105 r/min膜盘组应力情况
由图5可得:转速提高至1×105r/min时,复合工况下膜盘联轴器最大应力集中在外膜盘根部,最大应力为454.2×106Pa。
由图5(b)可得:膜盘危险应力区域分布不均匀,此时膜盘发生不对称弯曲。
接下来,笔者分析计算两种转速下联轴器危险应力和危险点安全系数。
联轴器不同转速时应力情况如表2所示。

表2 联轴器不同转速时应力情况
由于笔者设计的膜盘联轴器为薄壁焊接件,焊接后会产生焊接残余应力,该应力会影响膜盘的组织性能[18-19]。笔者参考标准《GB50341-2014》,设定膜盘联轴器膜盘组件最小设计安全系数为2.5。
设计安全系数n表示如下:
n≥2.5
(8)
原膜盘联轴器在1×105r/min转速下的安全系数小于设计要求,需要对联轴器进行优化。另外在高速旋转的复杂工况下,膜盘联轴器易产生非对称弯曲[20],需综合考虑联轴器的强度和动力学特性。
超高速膜盘联轴器设计的关键在于保证挠性的同时降低危险应力,即需要在降低联轴器弯曲刚度的基础上减小膜盘危险应力。
2.2 联轴器关键参数选取
针对高速挠性联轴器进行优化设计时,需要考虑应力和刚度条件。在降低联轴器危险应力时,其刚度需要尽可能小,以保证联轴器具有足够的挠性,降低两端支撑的反作用载荷[21]。
联轴器膜盘组件关键参数如图6所示。
考虑联轴器安装和建模关系,笔者初选D、D3、h、h1、h2、h3为设计参数。膜盘组件其他参数由装配及设计关系给出。
为找到影响联轴器强度和弯曲刚度的关键参数,笔者设计了正交实验,如表3所示[22]。
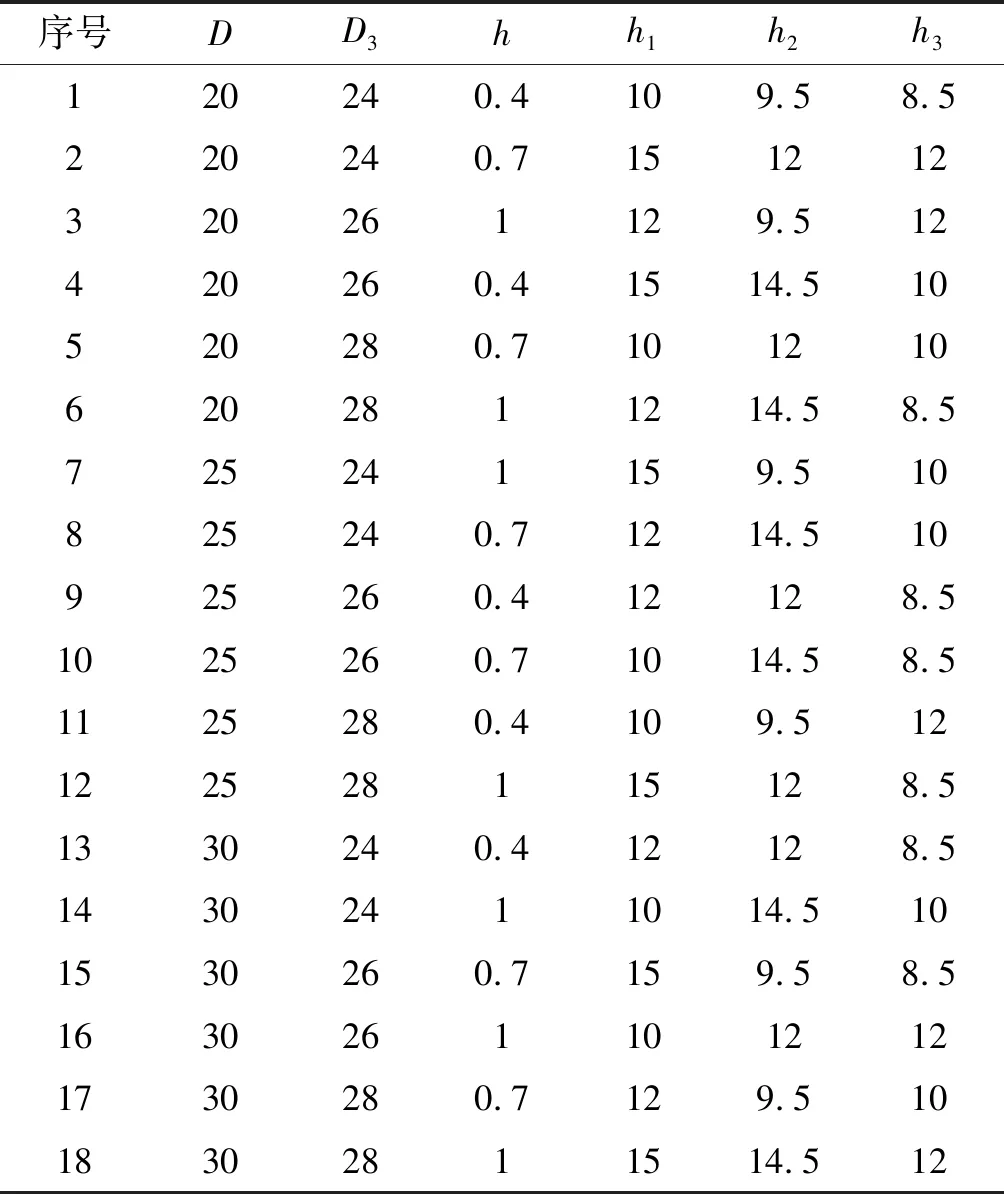
表3 正交实验设计表
将表3数据代入有限元仿真软件中,可以得到正交实验结果,如图7所示。

图7 正交实验应力与弯曲刚度结果
笔者对图7仿真结果进行多因素方差分析,求得危险应力第三类平方和SSR(Ⅲ)、自由度df、均方E(x2)及对应显著性P关系,如表4所示。

表4 应力多因素参数分析
经多因素方差分析后,可以得到弯曲刚度的第三类平方和SSR(Ⅲ)、自由度df、均方E(x2)及对应显著性P,如表5所示。

表5 弯曲刚度多因素参数分析
笔者针对D、D3、h、h1、h2、h3这六个参数进行多因素方差分析,结果发现,外膜盘外径D和膜盘厚度h对膜盘应力有显著影响,外膜盘外径D和外膜盘长度h1的显著性P值接近设定值,D和h1对联轴器整体弯曲刚度有明显影响作用。
考虑弯曲刚度和危险应力设计要求,笔者综合选取参数D、h和h1为后续设计关键参数。
2.3 目标函数求解
笔者采用拉丁超立方方程随机生成55组参数,利用有限元软件,求解得到了多组仿真结果,如表6所示。
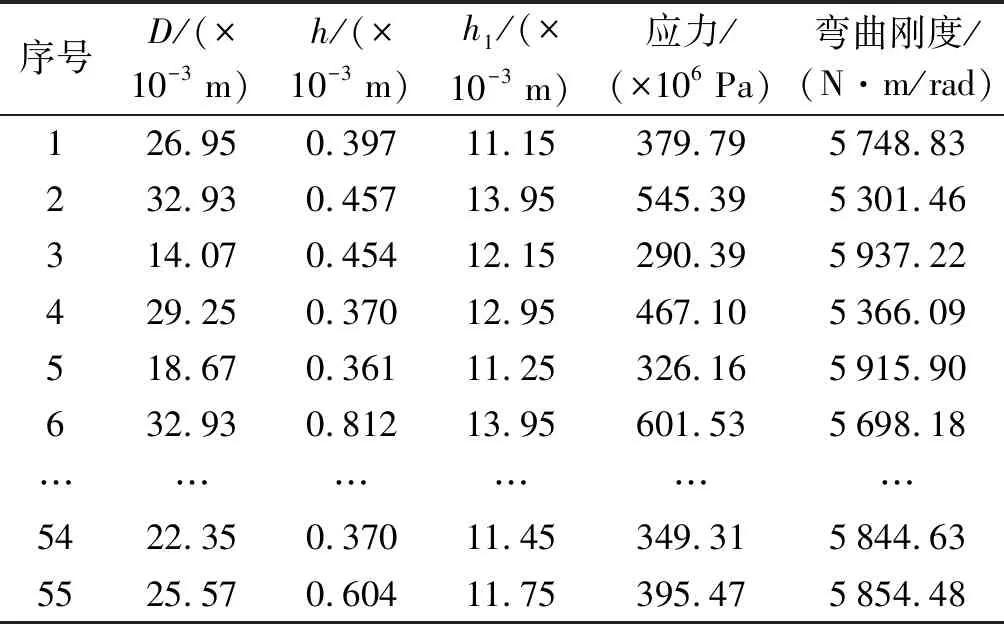
表6 55组仿真样本点
2.3.1 多项式逼近
假定外膜盘外径D、膜盘厚度h、外膜盘长度h1与危险应力的函数关系式为,与弯曲刚度的数学关系式为K。
从图7中随机选择7组正交实验结果代入式(1)、式(2),计算结果表示如下:
(9)
(10)
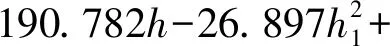
(11)
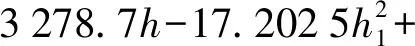
(12)
危险应力多项式拟合计算值与仿真计算结果对比图如图8所示。

图8 危险应力多项式拟合结果与仿真结果对比图
弯曲刚度多项式拟合结果与仿真结果对比图如图9所示。

图9 弯曲刚度多项式拟合结果与仿真结果对比图
多项式的项数越多,逼近的精度越高。但是采用多项式的项数总是有限的,精度不容易满足要求。
由图8、图9可知:多项式计算值与仿真结果差异较大,其中应力拟合误差平均值达22.51%,弯曲刚度误差达3.69%。
2.3.2 神经网络拟合法
反向传播神经网络擅长处理输入与输出因素间复杂的多元非线性关系。笔者利用反向传播神经网络研究输入参数与输出变量间的定性关系,找到关键参数与危险应力和弯曲刚度间的函数表达式,结果如图10所示。
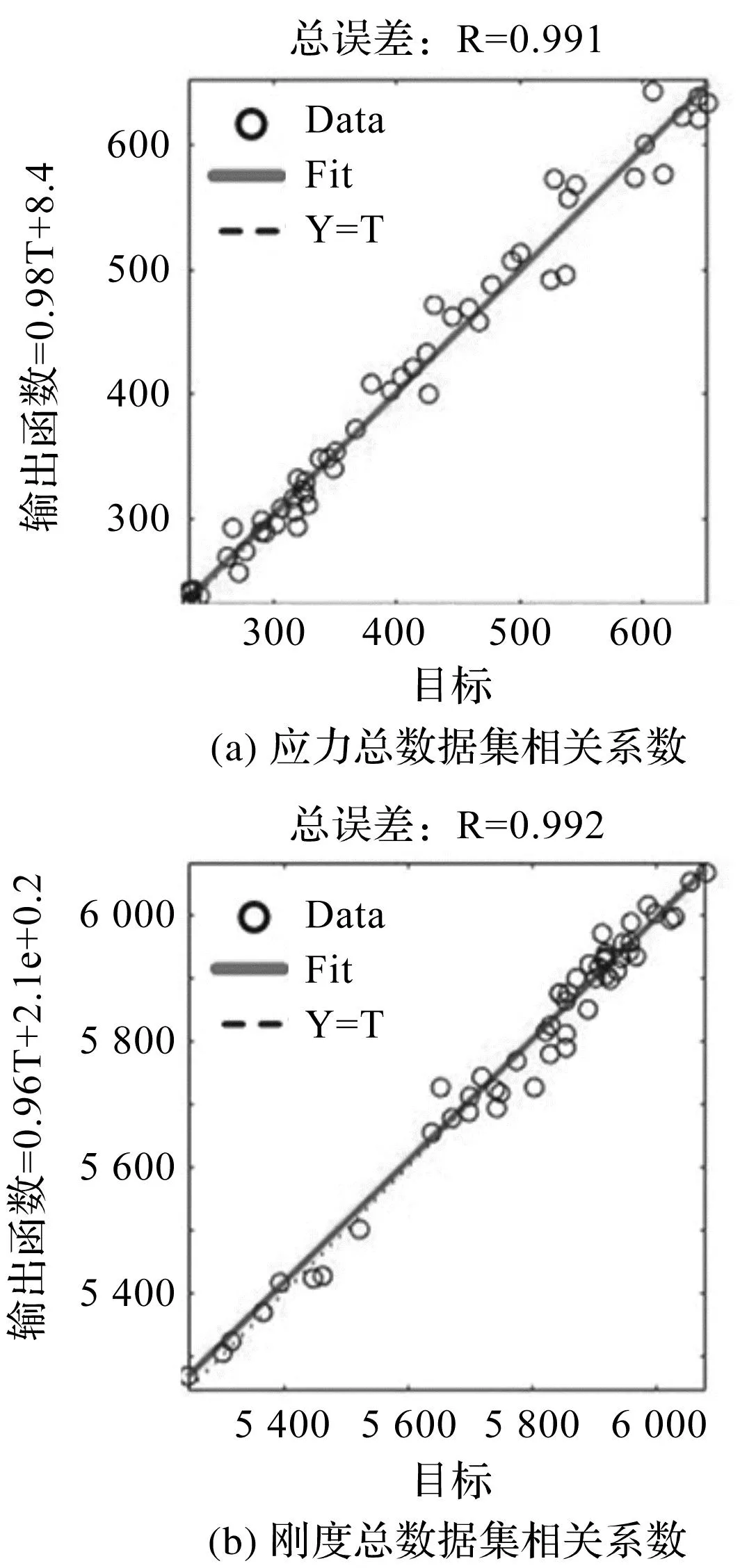
图10 反向传播神经网络预测结果与仿真结果对比图
由图10可得:反向传播神经网络预测效果良好,危险应力预测值与仿真结果的训练误差为0.942%,测试误差为0.727%,总误差为0.948%;弯曲刚度预测值与仿真结果的训练误差0.771%,测试误差为14.371%,总误差为2.927%。
由此可见,反向传播神经网络拟合误差结果远小于多项式拟合误差结果。
2.4 多目标优化
笔者利用遗传算法函数对上面求得的应力预测函数f和弯曲刚度预测函数K进行多目标优化求解,得到的结果如表7所示。

表7 多目标优化Pareto解集
表7所示的Pareto解集中,里面的每一个解都是优化解。一方面,为满足试件加工需求,薄壁膜盘厚度不能太小;另一方面,为减轻联轴器质量,膜盘外径和膜盘厚度又不能太大。因此,膜盘厚度需要取适中值,膜盘外径应尽可能小。在满足上述需求的同时,还需减小联轴器弯曲刚度,这要求外膜盘长度合适。
综上,笔者选取一组优化参数为25.253×10-3m、0.406×10-3m及15×10-3m。
笔者比较所有多目标优化预测结果与仿真结果,求得18组预测值与仿真结果的相对误差分布情况,如图11所示。

图11 多目标优化结果与仿真结果对比图
由图11可知:多目标优化后得到的应力预测值与仿真计算值最小相对误差为0.42%,平均相对误差为2.74%,最大相对误差为5.59%;弯曲刚度预测值与仿真计算值最小相对误差为0.23%,平均相对误差为1.52%,最大相对误差为4.45%。
由此可见,通过反向传播神经网络拟合结合遗传多目标优化得到的优化Pareto解集是可靠的。
2.5 有限元验证
笔者采用有限元分析软件,求解了复杂工况下,优化后联轴器模型的仿真结果,如图12所示。

图12 仿真结果
优化后膜盘联轴器最大应力值为371.48×106Pa,此时最大应力位于外膜盘根部。
优化前后对比结果如表8所示。

表8 优化结果
由表8可知:优化后的联轴器危险应力为371.48×106Pa,降低了18.2%;弯曲刚度为5 428.89 N·m/rad,降低了5.05%;优化后的联轴器安全系数为2.69。
由此可见,优化后的联轴器强度及刚度都满足优化目标。
比较优化后联轴器的补偿能力性能,即其计算结果如表9所示。

表9 优化联轴器补偿能力
由表9可知:优化后联轴器允许最大平行不对中为0.38×10-3m,最大角向不对中值为0.4°,允许复合不对中值为0.3×10-3m(平行)、0.3°(角度)。
由此可见,优化后联轴器的补偿能力明显提高。
3 结束语
针对联轴器高转速、复合工况下的优化问题,笔者采用反向传播神经网络和多目标优化遗传算法相结合的方法,对膜盘联轴器进行了参数优化;优化后,联轴器强度和动力学特性均得到了明显改善;最后,结合有限元分析,对优化预测的准确性进行了验证。
研究结论如下:
1)膜盘联轴器在高转速、复合不对中的影响下,联轴器膜盘发生不对称弯曲和应力集中现象。联轴器危险应力超过设计要求;
2)柔性联轴器危险应力受外膜盘外径D和膜盘厚度h影响较大,弯曲刚度受外膜盘外径D和膜盘长度h1影响较大;
3)对比多项式拟合和反向传播神经网络拟合可知,预测结果较为可靠。多目标优化后,联轴器补偿不对中能力得到了提升,联轴器危险应力下降了18.2%,弯曲刚度值下降了5.05%,优化效果良好。
由于联轴器实验转速高、实验条件复杂,短时间内无法完成现场实验。因此,在下一阶段,笔者将开展相关实验,以验证上述优化结果是否可靠。

