基于预训练GoogleNet模型和迁移学习的齿轮箱故障检测方法*

杨魏华,阮爱国,黄国勇

(1.昆明理工大学 民航与航空学院,云南 昆明 650500;2.文山苗族壮族自治州高级技工学校,云南 文山 663000;3.中国广核新能源控股有限公司云南分公司,云南 昆明 650000)

0 引 言

在工业生产中,齿轮箱作为动力传递装置,长期处在润滑不良、载荷突变等恶劣工况下,致使齿轮工作表面容易发生磨损、裂纹、断齿等故障,严重影响了动力传递系统的可靠性。齿轮箱出现故障也会造成巨大的损失。目前,齿轮箱的故障检测方法主要有人工定期检查、无损检测、振动信号监测[1]等。基于振动信号的检测方法在后期处理过程中具有技术上的优势,因此逐渐成为旋转件故障检测的主流方式。

樊家伟等人[2]使用振动信号做快速傅里叶变换,然后将其用于长短期记忆网络,对不同局部的齿轮箱进行了故障诊断;但该方法选用了部分频段作为特征数据,易造成特征模糊等问题,无法对故障进行预判。包文杰等人[3]使用快速优化的短时傅里叶方法对行星齿轮进行了故障诊断,结果表明该方法得到的能量分布更为集中;但该方法未对信号进行去噪处理,在强噪音背景下具有一定的局限性。陈仁祥等人[4]针对工程数据难于满足独立同分布等问题,提出了一种深度置信网络以用于齿轮箱故障诊断,并验证了该方法的可行性;但该方法采用原始信号作为源域数据对模型进行训练,训练过程中存在人为调参量大的问题。SHAO Si-yu等人[5]提出了一种基于VGG-16模型与迁移学习的故障诊断方法,并将其用于齿轮箱故障诊断,结果表明该方法具有较高的识别率和更短的训练时间;但该方法局限在于其使用的数据为原始数据,未进行必要的预处理。

院老虎等人[6]提出了一种AlexNet模型与迁移学习相结合的轴承故障分类方法,并证明了该方法在可用数据较少的情况下能达到较高的诊断精度;但该方法使用一维信号作为数据输入,容易造成特征识别率低等问题。ZHANG Ma-Ping等人[7]提出了一种AlexNet模型与迁移学习相结合的方法,并在轴承故障诊断中进行了验证。CAO Pei等人[8]提出了一种深度卷积网络的迁移学习框架,此方法涵盖了特征值的自动提取以及类别判断的功能;但该方法使用原始信号作为输入数据,在实际工作环境中,噪音含量较大,对特征提取影响较大。CHEN Ren-xiang等人[9]结合了卷积神经网络(CNN)和离散小波变换,并将其用于齿轮箱故障诊断,结果表明该方法具有较高的精度;但该方法的主要局限在于需要大量数据对网络进行训练。王军辉等人[10]针对迁移学习中源域和目标域分布差异问题,提出了动态域适应的轴承诊断方法,结果表明,该方法能有效提高跨域诊断精度;但该方法使用原始信号进行CWT变换,会造成小波尺度图特征模糊。侯召国等人[11]提出了一种基于迁移学习与加权多通道融合的诊断方法,并在齿轮箱故障诊断中得以验证;但该方法使用多通道融合数据预训练网络,对数据量的要求较高,实际工程中很难用于有效采集大量数据。刘飞等人[12]提出了迁移学习和深度残差网络的算法,将其用于滚动轴承,并取得了较高的精度;但该方法主要局限在于使用原始信号进行二维转换,时频图含有干扰成分。

上述学者的研究表明,深度网络用于故障诊断能够较大程度提高诊断精度和诊断效率。

基于上述学者的研究成果以及研究中存在的问题,笔者提出对信号进行去噪处理,然后将其转化为二维尺度图用于网络训练,最后利用知识迁移的特点,把模型已经学到的知识用于新任务的处理。

1 信号预处理

若把齿轮箱看作一个系统,单位脉冲响应函数为k(t),则传感器采集到的信号如下[13]:

(1)

式中:dj为齿轮故障冲击强度系数;s(t)为齿轮箱实际冲击信号;h(t)为其他分量信号;Tr为齿轮故障冲击周期。

噪音掺杂于信号,易造成齿轮箱有用特征模糊等问题,导致神经网络对故障特征识别率下降,为了突出故障的有用特征,增加网络对故障特征的识别率,需要对信号进行去噪处理,去噪后故障特征更为突出,故笔者采用小波阈值去噪法对信号进行去噪处理。

信号去噪前后的二维尺度如图1所示。

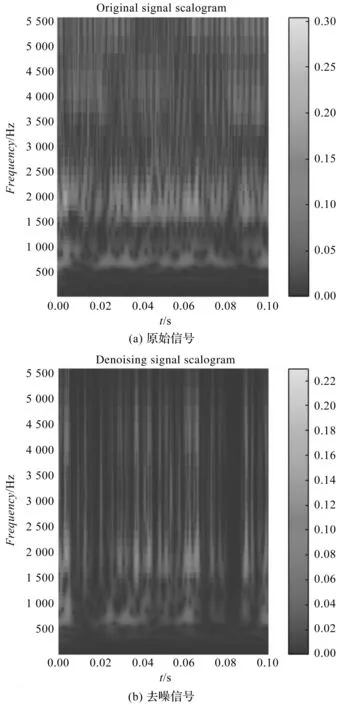
图1 原信号与去噪信号尺度图

由图1(a)可知:原始信号中特征混杂,齿轮冲击频率没有明显的区分界限;通过图1(b)可以发现,齿轮冲击特征较为明显,没有多余的混杂成份。

1.1 小波阈值去噪

小波阈值去噪法是1992年JOHNSTONE和DON-OHO教授首次提出的[14-15]。

对于任意能量有限的信号,小波变换公式为:

(2)

式中:Wf(a,b)为小波系数;a为尺度因子,a≠0;b为平移因子,b∈R。

在信号空间L2(R)中,小波重构的逆变换公式如下[16]:

(3)

根据以上小波理论,选择适合的小波基函数以及量化阈值,即可对信号进行分解与重构。笔者选用软阈值进行量化处理,其表达式为:

(4)

为了说明该方法的可行性,笔者对原始信号及降噪信号在时域内进行了可视化处理,如图2所示。

图2 原始信号与去噪信号

由图2(a)可以清楚发现:噪音掺杂于整个信号区间,难于区分有用信号成分;通过图2(b)能清楚发现噪音部分已被过滤,只剩有用信号成分。

1.2 二维尺度图获取

一维信号转变为二维图片的方法较多,连续小波变换(CWT)因其能同时在时间域和频率域刻画原始信号被广泛应用。

笔者选择波形与齿轮箱冲击特性较为接近的Morlet小波对信号进行二维尺度图的转化。

一维振动信号转二维小波尺度图流程如图3所示。

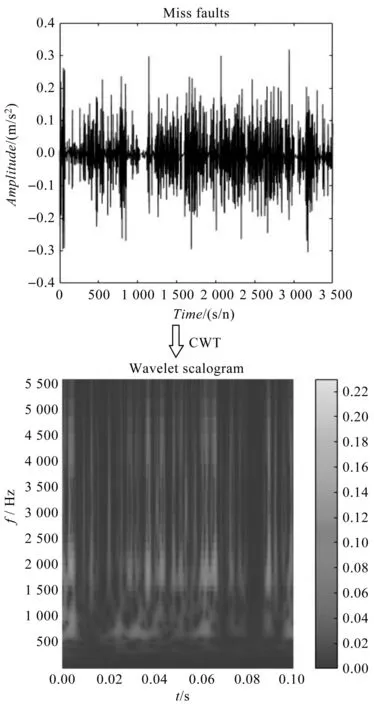
图3 振动信号转小波尺度图

由图3可知:通过CWT能将一维信号转变为二维小波尺度图,且小波尺度图能同时描述时间域和频率域特征。

2 GoogleNet模型与迁移学习

2.1 迁移学习

迁移学习是指把先前已有的知识用于相近领域或任务的一种算法,是深度学习的一个子集。把学习知识的领域称为源领域(source domain),待解决的领域称为目标域(target domain),源域对应原任务,目标域对应目标任务。迁移学习中,只需要使用少量的标签数据训练微调后的网络即可达到较好的分类效果,同时可以节省计算成本和训练开销。

迁移学习的定义为:

给定一个源域DS={xi,yi}(i=1,2……ns)和目标域DT={xj,yj}(j=1,2……NT),当迁移条件成立时,模型利用源域数据学得的知识去逼近一个目标域上的预测函数f(·),让f(·)在目标域上达到最大的预测准确度。其表达式如下[17]:

(5)

式中:l(·,·)为预测误差;f(·)为预测函数。

2.2 预训练GoogleNet模型及微调

GoogleNet模型是基于大型图像数据集ImageNet训练的图像分类网络,其能够对1 000个类别图像进行分类。GoogleNet网络模型包含了2个二维卷积层,9个inception模块,2个最大池层和1个平均池化层。

模型具体结构参数(修改自文献[18])如表1所示。

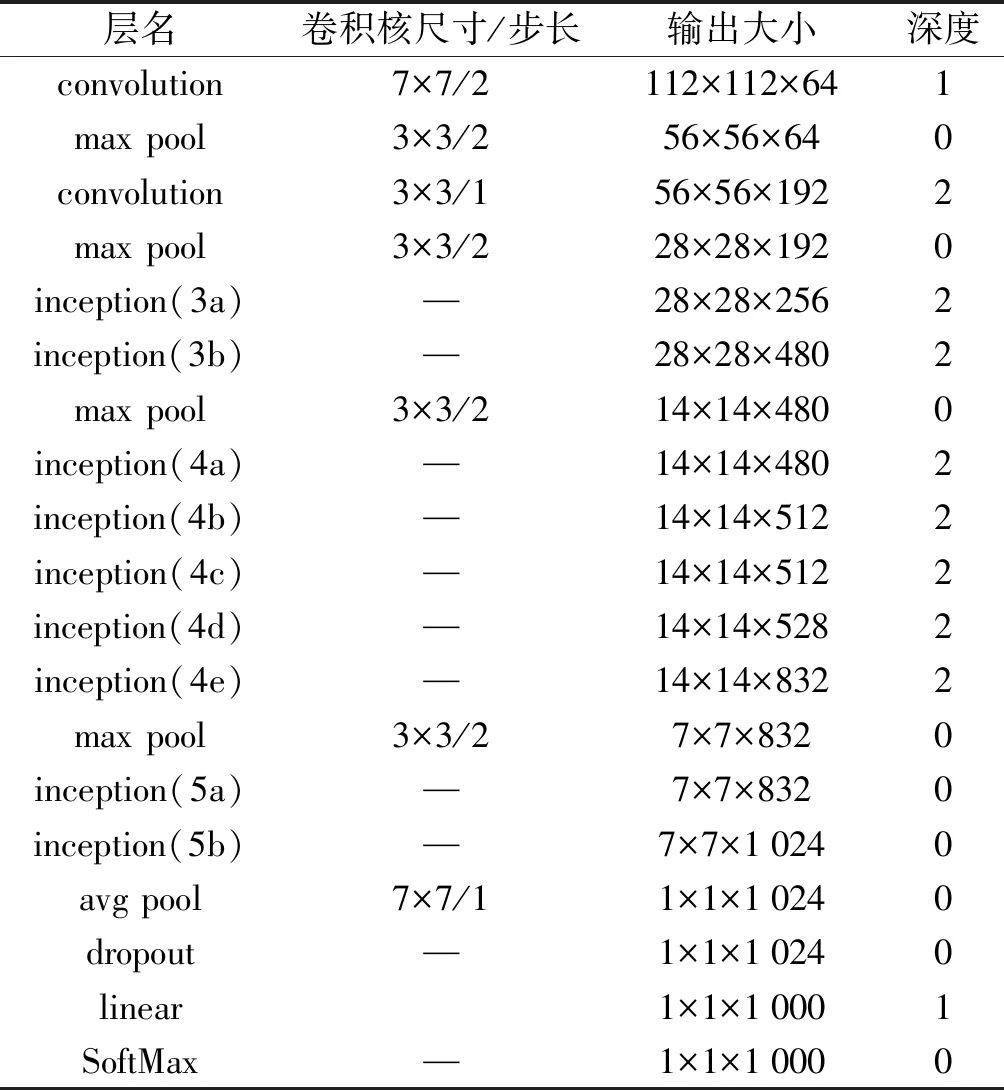
表1 GoogleNet网络参数

GoogleNet模型中所有的激活函数均为ReLU函数,其表达式如下:

(6)

概率输出函数为SoftMax函数,其表达式如式下:

(7)

式中:Pk为第k个类的概率值;j为类的总数。

平均池化、最大池化操作表达式如下[19]:

(8)

(9)

由表1可知:该模型第二个卷积层使用了更小的卷积核,同时使用了9个inception模块和批量归一化层(batch normalization, BN)以改善模型计算速度。但从零开始训练模型对计算机算力以及数据量要求依然较高,训练开销依然较大,使用预训练模型微调进行迁移学习可以很大程度改善上述问题。

笔者使用预训练GoogleNet模型对其结构进行微调,然后将其用于齿轮箱故障分类任务,将GoogleNet模型的全连接层(Fc)、SoftMax层以及Output层输出类别替换为和故障类别相对的节点数,模型剩余层参数保持不变。此时模型被分为保留层和更换层,在新模型训练时,对保留层参数进行冻结,使用少量样本训练更换的新层即可。

图4 基于GoogleNet的迁移学习诊断模型

由图4可知:利用源域数据对模型进行预训练,达到要求后保存模型参数,然后对预训练模型进行微调,模型中保留层将被迁移至目标域,此时保留层参数保持不变,只需对更换层参数进行微调即可。

3 实验验证与分析

3.1 实验数据说明

为验证基于预训练GoogleNet的迁移学习模型可行性,笔者使用平行齿轮箱数据和行星齿轮箱数据对其进行验证。

其中,平行齿轮箱数据来自于昆明理工大学控制与优化重点实验室。行星齿轮箱数据来自于东南大学齿轮箱公开数据。

平行齿轮箱数据采集于负载为0 N、2 N、4 N、6 N,四种不同工况下的断齿(Miss)故障状态和健康(Health)状态数据,其中,采样频率为12 800 Hz,电机转速为800 r/min。

行星齿轮箱数据采集于负载为0 V,采样频率为20 Hz,电机转速为1 200 r/min,以及采样频率为30 Hz,电机转速为1 800 r/min,负载为2 V的两种工况数据。

其中包含的故障类型为5类,分别是齿缺损(Chipped)、断齿(Miss)、齿根部磨损(Root)、齿面磨损(Surface)、正常(Health)[20-22]。

3.2 样本集构建

为了保证有足够的样本用于模型的训练,笔者采用滑窗切割信号进行样本扩充。行星齿轮箱样本按2 048个点分割,1 024个点为重叠度;平行齿轮箱样本按1 926个点切割,963个点为重叠度。保证切割的每一个样本覆盖完整的齿轮运行周期。

由于教育教学督导和评价机制的主要目的是督促和引导教学良性发展，使教师的教学工作和学生的学习效果都有提升，所以，教育教学督导和评价机制的建立、发展和完善都与学校和学院的教学质量保障和建设息息相关。因此针对教师的教育教学督导和评价机制提出以下的改进办法：

样本扩充方法如图5所示。

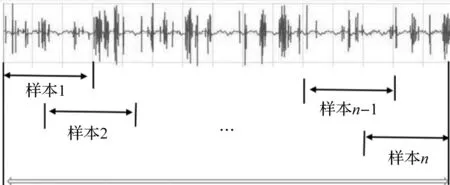
图5 信号重叠采样

由图5可知:采用重叠采样法能有效地扩充样本数量,且50%重叠度能有效保证每个样本覆盖齿轮运行的完整周期,齿轮故障特征更为完整。

笔者按上述方法对不同工况下的信号进行CWT变换,行星齿轮箱0 V工况得到样本5 000份,2 V工况得到样本5 000份;平行齿轮箱6 N工况得到128份样本。行星齿轮箱训练集和测试集样本按6 ∶4比例划分,单工况获得训练样本3 000份,测试样本2 000份;平行齿轮箱按照5 ∶5比例划分,单工况得到训练样本64份,测试样本64份,如表2所示。

表2 样本划分

由表2可知:用于模型训练的样本数据较少,属于典型的少样本问题,该情况更能检验迁移学习模型在少样本情况下的鲁棒性。

3.3 实验步骤与结果分析

笔者采用MATLAB深度网络设计器搭建了模型,并完成了模型训练,最后用测试集对模型进行了评估。具体的步骤如下:

1)加载预训练GoogleNet模型;

2)对模型的低层实行冻结,对网络高层进行微调,使神经元个数与故障类别对应;

3)将原具备1 000个分类的最后一个全连接和输出层替换为新的5分类和2分类的全连接层和输出层,并设置学习权重为10;

4)使用准备好的数据集对新层进行重新训练,训练过程中求解器选用Sgdm,初始学习率设置为10-3,批大小设置为100个,验证频率为10;

5)使用测试集对模型进行评估,绘制混淆矩阵。

3种工况的混淆矩阵如图6所示。

图6 3种工况混淆矩阵

根据处理得到的样本数据,笔者共设置了3类不同工况,具体如下:

工况1。样本数据来自电机转速1 200 r/min,采样频率20 Hz,负载为0 V的工况,测试集分类结果如图6(a)所示;

工况2。样本数据来自电机转速1 800 r/min,采样频率30 Hz,负载为2 V的工况,测试集分类结果如图6(b)所示;

工况3。样本数据来自电机转速800 r/min,采样频率12.8 kHz,负载为6 N的工况,测试集分类结果如图6(c)所示。

由图6可知:模型在工况1和工况2中分类准确率未能达到100%,有少量样本被错误分类;模型在工况3中的分类准确率达到了100%。

工况1、工况2中出现的误分类问题,是相同超参设置情况下模型过度学习导致的。

3次分类准确率如表3所示。

表3 分类准确率

由表3可知:模型在3类工况下均取得较高的分类准确率,3次分类结果的均值高达97.40%,说明了TL对解决少样本问题是有效的。

3.4 结果对比与分析

为了证明基于GoogleNet的迁移学习模型对于故障分类任务的优越性,笔者选用了部分诊断方法进行比较,其中包括1个含有2个二维卷积层的12层CNN模型,未经预训练过的GoogleNet模型。

其比较结果如图7所示。

图7 分类精确度及训练时间

由图7(a)可知:基于预训练GoogleNet的迁移学习模型在同类工况中的分类准确率高于其他两类模型;从图7(b)可知:基于预训练GoogleNet的迁移学习模型在工况1和工况2中的训练时间较少,具有较大优势,仅为766 s和796 s;在工况3中,基于预训练GoogleNet的迁移学习模型相比于未经预训练的GoogleNet模型,训练时间仍具有优势,相比于12层CNN模型,训练时间有所增加,这是12层CNN模型层数较少所导致的。

为了充分说明基于预训练GoogleNet的迁移学习模型的优越性,笔者对图7中3种CNN模型在3类不同工况下的准确率取均值,可视化数据分布结果如图8所示。

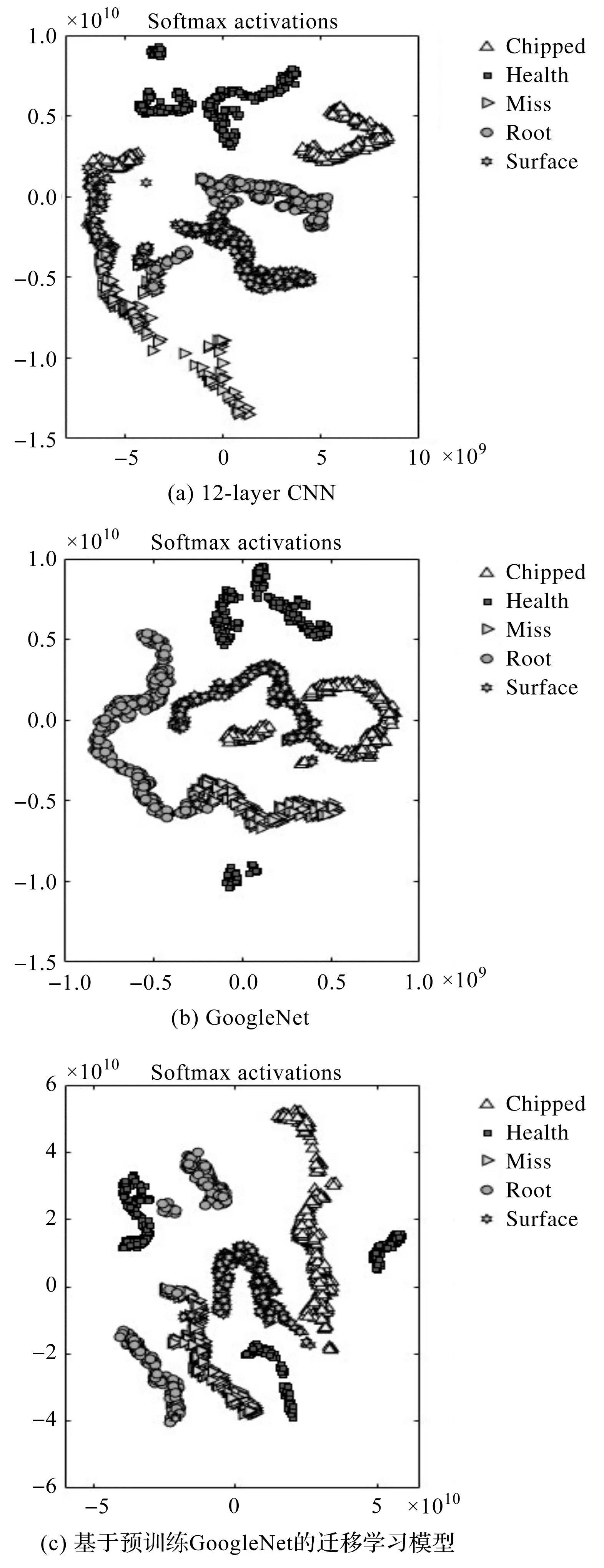
图8 3种CNN网络分类结果

由图8(a)分析可知:12层CNN模型对于不同故障类型的分类能力较差,图中各种故障数据混杂,聚类度较低;由图8(b)可知:大部分数据被网络聚类分离,只有少部分数据混杂,证明该网络具备较好的分类能力;由图8(c)可知:多数数据被网络聚类分离,只有少部分被错分,而且被错分的数量明显少于图8(b)中的数量,说明该网络具备较好的分类能力。

通过上述分析可知:基于预训练GoogleNet的迁移学习模型在齿轮箱故障分类问题中的精准度、训练时间上,相比于其他方法更有优势,而且能按照不同分类任务制定网络输出类别,在面对少量未知样本的情况时,仍具有较高的分类精准率,这进一步说明了基于预训练GoogleNet模型的迁移学习在故障诊断领域的可行性。

4 结束语

针对以往齿轮箱故障诊断中特征处理算法繁琐的问题,笔者提出了一种基于预训练GoogleNet模型和迁移学习的齿轮箱故障检测方法,并利用东南大学齿轮箱数据集和昆明理工大学齿轮箱数据集对该方法进行了验证。

研究结果表明:

1)相比于传统的CNN网络,基于预训练GoogleNet的迁移学习方法在目标域样本缺稀的情况下具有较高的故障分类能力,平均准确率高达97.40%;

2)相比于其他2种故障诊断方法,基于预训练GoogleNet的迁移学习模型训练时间较短(均值为766 s,远低于12层CNN的1 296 s,以及未经预训练GoogleNet模型的1 490 s),证明在节省训练开销和提高网络精准度方面,微调预训练模型实现迁移学习的方法是可行的;

3)在5分类问题中,模型准确率高达97.35%和97.40%,在2分类问题中,其分类准确率高达100%。这说明所提的微调模型高层的方法能根据目标任务分类情况个性化设置模型输出,用于不同的分类任务;且微调模型后只用训练模型更换层即可,能减少模型训练开销和超参试错开销,加快模型收敛,降低对计算机算力的要求。

笔者所提方法还存在一定的局限性,即当训练样本和测试样本所在领域不同,且特征分布差异较大时,会导致故障识别率不稳定。因此,在后续的工作中,笔者将对上述存在的问题做进一步的研究。