静听思维拔节的声音——“图形运动（三）解决问题”练习课教学实践与思考

浙江温州市仰义第一小学（325000） 林 迪

浙江温州市滨江外国语小学（325000） 林志辉

“图形运动（三）解决问题”练习课的教学要让学生能在方格纸上描述简单图形的平移、旋转、轴对称变换的运动过程，在观察、操作、想象、描述图形运动过程中，进一步感悟平面图形全等变换的特征，发展空间观念和推理意识。以下是笔者的教学实录。

一、轮廓划分，思维初拔节

（一）关键板的推理

【教学片段1】

师：通过课前学习单（如图1 所示），大家尝试了用七巧板拼搭小鱼图。在拼搭的过程中，你们先拼了几号板？又是如何拼其他板的？

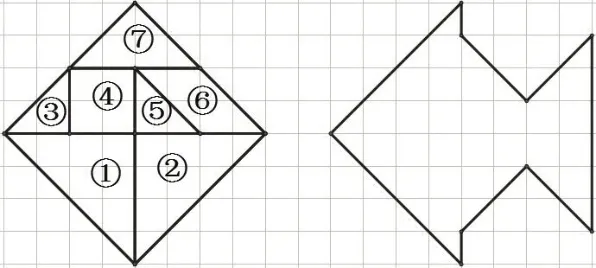
图1 利用七巧板拼搭小鱼图

生1：我先确定①号板或②号板，因为它们的面积最大，最好确定。

生2：我先确定④号板，因为它的形状特殊，它的4条边相等，有4个直角。

师：很多同学选择了④号板，这里有三种④号板的摆放位置（如图2），你同意哪一种？为什么？

图2 ④号板在小鱼图中的三个不同位置

生3：第三种。如果④号板的摆放位置是第一种或第二种，那七巧板中最大的①号板和②号板就摆不下了。

师：说一说按第三种摆放④号板后，其他板的位置。

生4：①号板和②号板在鱼头的位置，③号板和⑤号板分别在鱼肚中间正方形的上下处，⑥号板和⑦号板在鱼尾。

（教师让生4操作几何画板。）

设计意图：在前测中，有70%的学生需要借助实物划分小鱼图轮廓。在本环节中，笔者首先让学生自主选择关键板，根据学生选择最多的④号板开展教学，让学生通过④号板的位置来推断其他板的位置，从而感受到用推理和想象来解决问题。笔者利用几何画板的强大互动性，让学生边说明边演示，直观展示他们的想象和推理过程。这样的设计旨在激发学生的思维，让他们亲身参与解决问题的过程，加深对数学知识的理解和记忆，并培养他们在数学学习中的兴趣和积极性。

（二）任意板的推理

【教学片段2】

师：还可以先确定几号板的位置，从而推理出其他板的位置？

生1：还可以先确定⑥号板和⑦号板的位置，因为小鱼图中⑥号板要和⑦号板放在一起，所以只能把它们放鱼肚或鱼尾，它们的位置确定了，①号板和②号板就只能放在鱼头，那其他板的位置也就确定了。

生2：还可以先确定③号板的位置，因为它只能放在鱼身，或放在鱼尾的最上方或最下方，它和⑤号板刚好是一上一下摆放，它的位置确定了，⑤号板的位置也就确定了。而③号板和⑤号板的中间只能摆④号板，再加上①号板和②号板在鱼头，其他板的位置也就确定了。

生3：我发现任意一块板的位置确定了，就能根据板之间的形状关系，确定其他板的位置。

设计意图：利用“还可以先确定几号板的位置”这样的问题，能让学生把根据④号板推理其他板的活动经验迁移到任意板的推理过程中。从最初只有某一块特定板是关键板，扩展为每一块板都可能成为关键板，学生利用图形几何特征进行轮廓划分，推理意识得到进一步发展。

二、运动描述，思维再拔节

（一）激活认知，唤醒经验

【教学片段3】

师：想一想，④号板是如何从图3-1 的位置运动到图3-2 的位置的？你能找出几种不同的运动方法？如果运动1 次记1 分，哪种运动方法的分数最低？

图3-2

生1：④号板先向下平移1 格，再向右平移12格，运动了2次，记2分。

生2：④号板先向右平移12 格，再向下平移1格，也是记2分。

（教师利用几何画板动态演示学生的方法。）

设计意图：通过描述④号板的运动路径，唤醒学生描述图形运动的数学学习经验。

（二）自主探究，表征互译

【教学片段4】

师：请将⑦号板从图4-1 的位置运动到图4-2中，并记分。

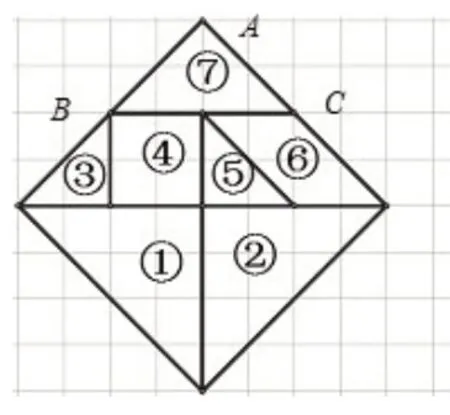
图4-1

生1：⑦号板绕点C逆时针旋转90°，向右平移12格，向下平移1格，记3分。

生2：⑦号板绕点A逆时针旋转90°，向右平移12格，向下平移5格，记3分。

生3：⑦号板绕点B逆时针旋转90°，向下平移5格，向右平移16格，记3分。

设计意图：学生通过语言、操作积累组合运动的描述经验，能够更好地理解和运用图形与几何的概念和原理，同时提高表达能力和思维的灵活性，空间观念也得到提升和发展。

（三）逐板分析，思维拔节

【教学片段5】

师：有哪些板的运动计分是2 分？利用学习单想一想、写一写。

生1：①号板需要1 次旋转和1 次平移，⑤号板需要平移两次，因此都记2 分。②号板需要1 次平移和1次旋转才能运动到目标位置，记2分。

生2：不对，②号板只要1次轴对称运动就可以了（图略），这样只记1分。

生3：那其他板也可以用轴对称的方法，这样能够减少运动的次数。

师：大家一起试试吧。

设计意图：借助“哪些板的运动记分是2 分”的问题，促使学生主动思考，并以②号板作为突破口，唤醒学生对轴对称运动的学习经验。

三、联结融通，思维三拔节

（一）推理想象拼帆船

【教学片段6】

师：七巧板不仅可以拼成小鱼图，还可以拼成帆船。看帆船图（图略），你把几号板当作关键板？

生1：①号板和②号板，因为它们的面积最大。

师（出示图5-1、5-2、5-3）：有三位同学确定了①号板和②号板的位置，你赞成哪种想法？

图5-1

生2：我赞成图5-2 的摆法。因为如果按图5-1 和图5-3 的摆法，④号板和⑥号板就不能同时摆进去，会有部分超出帆船的轮廓。

设计意图：本环节利用将七巧板拼成帆船图的问题情境，引导学生正向迁移通过想象推理划分轮廓的数学活动经验，展现严谨的推理思路。

（二）思考迭代算总分

【教学片段7】

师：想一想，在所有板的运动中，哪块板的运动记分最低，是多少？

生1：④号板只需要1 次平移就可以实现，记1分。

生2：我发现①～⑥号板都只需要1次轴对称运动，都是记1分。

生3：我认为所有板的运动总分是6+3=9（分），因为①～⑥号板只需要1 次轴对称运动，共6 分，⑦号板的运动记3分。

生4：我发现的方法总计分更低，因为①～⑥号板可以整体进行1次轴对称，记1分，⑦号板的运动记3分，所以总计1+3=4（分）。

生5：我发现最低分是1+1=2（分），①～⑦号板整体进行1 次轴对称，共1 分，⑦号板旋转1 次记1分。

（教师给予每个学生充分的时间进行空间想象，然后利用几何画板进行演示，从而验证学生的想法。生5的想法如图6所示。）

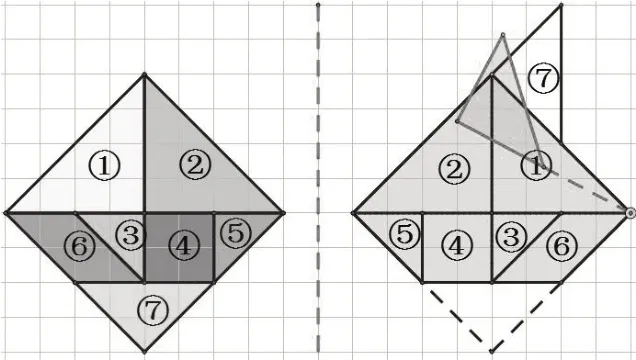
图6

设计意图：从单块板的运动逐步提升到组合板的运动的过程中，学生需要掌握图形的特征，平移、旋转、轴对称的特点，能够简洁地描述图形的运动。在总分逐步减少的过程中，学生的空间观念逐步发展。

（三）迁移经验促融通

【教学片段8】

师：回看图4-1和图4-2，现在你认为⑦号板运动最低记几分？

生：1 分。因为可以通过一次旋转到达目标位置。

（教师利用几何画板显示⑦号板的运动路径，如图7所示。）

图7

师：大家重新思考一下，七巧板运动成小鱼图，每块板的运动最低分是几分？

……

设计意图：七巧板运动分总分逐渐减少的过程，一次又一次地打破学生的思维定式，目光从部分到整体，旋转中心从图形中到图形外，最后回头看之前问题中⑦号板的运动，学生顿感“柳暗花明又一村”，思维的拔节清晰可见。

四、教学反思

在活动中，学生用语言描述图形的拼摆，并结合几何画板进行操作，实现了语言和演示的同步性。根据学生对运动方式、路径描述的不同，教师现场生成与语言描述相匹配的动态演示，以直观的方式展示学生难以用语言描述或想象的运动路径，促使学生建立丰富的表象。

几何画板具有强大的交互性和直观性，它能够不断拓宽学生想象的空间，并提供可视化的动态表征，为学生的思维拔节提供了丰富的表象支持，帮助学生更好地理解和探索平面图形的运动特性，培养学生的空间思维和创造力。