基于速度特征的内河LNG船舶三维动态安全区建模方法

陈立家,王 冰,吴小红,李胜为

(1.武汉理工大学 航运学院,湖北 武汉 430063;2.武汉理工大学 内河航运技术湖北省重点实验室,湖北 武汉 430063)

0 引 言

LNG船舶作为天然气的水上运输工具,具有易燃、易爆且单次运量大等特点。根据JTS 165—5—2021《液化天然气码头设计规范》的规定：LNG船舶在航行时,需要设置一定范围的安全区。内河航道由于复杂的交通流,其速度快慢对船舶的安全区有着相当大的影响。为此,有必要对LNG船舶的安全区进行精确量化分析,为其在内河航道通航标准的制定提供理论支撑。

基于此,学界就内河船舶模型进行了一系列的分析与优化。R.SZLAPCZYNSKI等[1]针对内河受限水域中的船舶展开研究,提出了一种新的船舶域模型,该模型考虑了船舶航行的特性,并通过船舶动力学模型确定了船舶域模型的边界算法;刘钊等[2]提出了一种考虑船舶避让紧迫度的数字化内河船舶领域建模方法,基于船舶的尺度、操纵性能等要素,通过解析法确定了船舶的领域边界。某些学者基于船舶领域理论,构建了LNG船舶安全区模型,以保障不同通航模式下LNG船舶的航行安全。LIU Jingxian等[3]基于经验值构建了一种纵、横向分别保持8、1倍船长的矩形移动安全区,用来评价影响LNG船舶通过航道的能力;廖诗管等[4]针对LNG船舶通航的特殊性,提出了一种船舶领域的实证方法,定量界定了LNG船舶移动安全区的尺度。总体而言,无论是船舶领域模型还是LNG船舶安全区模型,其尺度界定多是局限于在船舶周围建立的固定尺寸区域,无法反映出船舶在不同航速下安全区的大小。

基于此,根据内河航道的特点,笔者根据内河LNG船舶速度特性,采用威布尔分布模型来约束速度大小;通过域分解法将复杂的三维实体分解为两个简单的子域,并分区域生成与速度相对应的边界曲线模型(即基于四元理论构建的船舶二维动态安全区边界方程);在此基础上,考虑LNG船舶在经过内河狭窄、浅水水域时,因其周围流场变化,会使船体下沉,出现船体下沉量和操纵性能变差等现象,增加了船舶航行的垂向纬度;基于解析几何理论构建了垂向运动边界方程,利用子域交界面边界条件保证区域之间的连续性;从船舶间极限通过的安全性出发,基于停船视距、船间效应和岸吸效应分布来确定船舶的安全区长、短轴解析式,根据航道水深垂向约束,建立基于船舶下沉量的船舶安全区垂向轴解析式,以定量界定内河LNG船舶三维安全区的尺度;最后通过仿真实验验证了该模型的有效性。

1 三维动态安全区模型

LNG船舶三维动态安全区建模流程如图1。

图1 三维动态船舶安全区建模流程Fig.1 Modeling process of three-dimensional dynamic ship safety zone

1.1 速度特征函数

LNG船舶在内河航道航行过程中,因船舶交通流密集,通航环境复杂,船舶在不同时刻的前后状态不断变化,这会导致不同方位的危险度及船舶对危险的感知能力产生差异,从而影响船舶安全区的大小。LNG船舶在航行期间速度较快,且变化频繁,从安全角度出发,速度越快,其安全区模型也应越大,即LNG船舶安全区模型大小与速度快慢成正相关,故应将速度因素考虑到LNG船舶安全区中。

一般而言,传统速度模型描述的是速度随时间变化函数,如式(1)：

(1)

式中：f(χ)为速度时变函数。

内河航道的通航环境十分杂乱,船舶速度变化频繁而复杂,这种变化具有多峰值特点,难以用单一威布尔分布模型、正态分布模型或对数正态分布模型来拟合。混合威布尔分布模型只对x≥0有效,适合对船舶速度分布进行描述,且能对多种复杂不确定性因素进行分析,其模型符合实际,结果更加准确。故为准确描述内河交通流中速度的分布规律,笔者采用混合威布尔分布模型[5]来拟合。概率密度函数如式(2)：

(2)

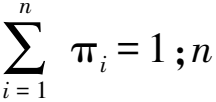
将式(2)代入式(1),变量t由虚拟尺度变量ρ替代,ρ由船舶速度变化决定,从而建立起船舶航行速度特征模型,如式(3)：

(3)

式中：Ξ=[ζ1,ζ2,ζ3]T为船舶速度状态向量,包括风、浪、水流等因素,满足0<ζi<1;Γ=[γ1,γ2,γ3]T为相同维数权重向量,0<γi<1;尺度参数ηi=||Γ||1,形状参数βi=1。

1.2 基于域分解的船舶三维安全区数学模型

1.2.1 坐标系及计算域

建立空间固定坐标系o-xyz,如图2。

图2 坐标系与计算域定义Fig.2 Definition diagram of coordinate system and calculation domain

图2中：坐标系原点为船舶中心,以右舷正横方向为x轴正方向,以船首向方向为y轴正方向,z轴正方向垂直xoy面向下,z=0位于静水面处。不考虑船舶与桥梁等的碰撞危险,以一个类似半球体ABC包住整个船舶,且固定于船体上。采用域分解方法将图2中的计算域划分为S1和S2两个子域,S1为包围船舶的水面以上区域,S2为水面以下区域。S1和S2与这两面同时相切的过渡区圆弧回转面连接。因此,船舶完整的三维安全区域WS可表示如式(4)：

WS=S1∪S2∪r1∪r2

(4)

1.2.2 船体水平面运动数学模型

船体在相对方位φ时安全区边界的相关参数如图3。图3中：Li为本船舶在相对方位φ时的安全尺度;x为其他船舶极限通过时的横坐标;y为其他船舶极限通过时的纵坐标。

图3 二维平面船舶安全区相关参数Fig.3 Relevant parameters of two-dimensional plane ship safety zone

考虑船舶安全区在不同方位上的差异性,借鉴四元船舶领域建模思想[6],考虑由船首尾及正横方向4条半径组成的四元组Q={Rbow,Rstern,Rport,Rstarboard}来刻画船舶安全区大小。建立二维船舶安全区边界方程如式(4)：

(4)

式中：f(·)为定义模型边界的函数;sgn(·)为符合函数。

sgn(·)由式(5)定义：

(5)

在船舶安全区边界基础上,引入速度动态函数k对模型进行动态调整,将单一模型问题转化为动态模型优化问题。则LNG船舶水平面安全区模型表达如式(6)：

(6)

1.2.3 船体纵垂面运动数学模型

需要考虑垂向运动对安全区的影响。垂向运动仅与速度v相关,即在垂直方向变化较大,故采用旋转抛物面作为安全区水面以下的模型,根据几何关系满足式(7)：

(7)

式中：Rvertical为垂向安全距离;vx为船舶水平面上的速度分量;vz为船舶速度的垂直分量。

1.2.4 交点边界交互

半径为r1、r2的圆分别与抛物线相切于B、B′,分别与椭圆相切于C、C′。圆弧BC、B′C′可表示为：

(8)

(9)

2 三维安全区边界解析计算

2.1 纵向制动的安全边界

内河可航行的水域宽度有限,LNG船舶只能沿着航道中心航行;LNG船舶因自身限制,当其他船舶在航道内无法完成追越时,只能以跟驰方式通过航道。基于跟驰-制动理论[7],LNG船舶的艏尾向的纵向尺度计算模型为：

Rbow=Rstern=l′+LS=vt+LS

(10)

式中：l′为相对航行距离;t为反应时间;LS为LNG船舶与目标船舶在同一航向上的制动距离。

LNG船舶倒车制动时,运动微分方程为：

(11)

式中：Tp为船舶螺旋桨产生的推力,N;R为船舶航行时的阻力,N;m、mx分别为船舶总质量和附加水质量,kg;a为船舶加速度,m/s2。

LNG船舶在内河航行时,所受阻力主要由风、水流等的作用[8],如式(12)：

R=R1+R2

(12)

式中：R1为风阻;R2为水流阻力。

船舶航行动力由螺旋桨提供,其推进力Tp为：

(13)

式中：CT为推力系数;nL为螺旋桨转速,r/s;DL为螺旋桨直径,m。

采用积分法对制动距离进行求解,如式(14)：

(14)

故船舶安全区艏尾向尺度与速度的函数表达如式(15)：

(15)

2.2 横向转向的安全边界

在内河狭窄水域中船-船效应是影响LNG船舶航行安全的一个重要因素。故将船-船效应的横向安全距离作为模型中左舷左正横的边界距离。船-船效应的数值计算采用文献[9]的通用计算模型。船舶横向漂移力和力矩可表示为：

(16)

式中：CFX为横向漂移力系数;CNX为转艏力矩系数;B为船宽;L为船长;d为船舶吃水;V1、V2分别为两船的速度。

由于内河航道普遍较窄,船舶易偏离中心航线靠向某一侧岸壁,此时还应考虑岸壁效应影响,故将基于岸壁效应的横向安全距离作为新模型右舷右正横的边界距离。岸吸力和岸推力矩的计算可参考文献[8]。

基于MMG理论,建立了三自由度船舶运动模型,将其线性化并应用拉普拉斯变换和逆运算,得到二阶响应模型,如式(17)：

(17)

式中：无量纲流体力学导数可由文献[10]中的方程确定。

根据所建立的MMG模型,获得了衡量LNG船舶操纵性能的船舶回转直径DT和进距AD,如图4。

图4 船舶转弯所覆盖区域Fig.4 The coverage area of ship turning

基于圆周运动学原理,以船舶90°转向时所覆盖的最大范围作为船舶安全区的参考边界,即图4中的虚线即为本船左舷左正横和右舷右正横这两个象限的区域,如式(18)：

(18)

2.3 垂向下沉的安全边界

随着船速增加,LNG船舶附近水位下降,由此会产生明显的船体下沉现象,这使得富余安全水深减少,影响到船舶安全航行。为确保航行安全,必须采取合理的操纵措施,避免因船速过快形成的下沉量而导致搁浅、触底风险。因此,LNG船舶动态安全区的垂向边界主要考虑因素是船体下沉量,如图5。

图5 垂向运动高度示意Fig.5 Schematic diagram of vertical motion height

船体下沉量是一个动态的变化量,其计算是制约船舶安全区垂向边界的关键因素。在船型和吃水固定不变情况下,船体下沉量会随船速增加逐渐加大,即与航速呈正比例关系,可用船速无因次量傅汝德数Fr来表示为：

(19)

式中：LPP为垂线间长。

运用经验公式确定LNG船舶各航速下的下沉量,则船舶动态下沉量Sb的计算如式(20)：

(20)

由图5可得出水线面以下边界关系：

Rvertical=d+Sb+h0

(21)

式中：h0为其他富裕深度,通常取船舶吃水的15%。

3 LNG船舶安全区结果分析

3.1 LNG船舶参数

LNG船舶船长127 m,宽19 m,航速4～12 kn,其主尺度如表1,其他基本参数详见文献[12]。LNG船舶动态安全区模型中对速度参数、输入变量(为航行环境风、浪、流的干扰)取值范围均为[-1,0],其中“-1”表示最恶劣的环境条件,“0”为最理想的状态。

表1 样本船舶主尺度Table 1 Principal dimensions of sample ships

3.2 不同速度下LNG船舶安全区结果分析

3.2.1 二维平面安全区结果分析

根据LNG船舶数据,基于安全区模型进行仿真,得到了在不同航速下的安全区边界,如图6;速度对安全区各边界的影响如图7。

由图6、图7可知：速度对动态安全区的影响相对较大,随着船舶速度增加,其安全区也随之增加。安全区在船艏尾向增长与左右横向增长是不同的,长轴随船舶速度增加幅度要远远大于短轴,速度每增加2 kt,安全区长轴增大约为100 m,短轴增大约为40 m,究其原因是船舶速度一般是指船艏向的位移速度,在速度影响下趋于向前部安全区域扩展变形,促使船艏向安全区域逐渐增大,即扩大了船舶在受影响方向上的边界距离。安全区右侧长度明显大于左侧,这也是为确保当船舶正横前来船时,留有足够水域以便船舶向右转向;同时由于安全区容易在速度影响下其最大区域优先扩展,这也导致了安全区几何形状趋于不规则。

图6 不同航速下的船舶安全区Fig.6 Ship safety zone at different speeds

图7 速度对船舶安全区各边界影响Fig.7 Influence of speed on the boundaries of ship safety zone

3.2.2 三维动态安全区结果分析

基于MATLAB,绘制练了LNG船舶的动态安全区空间三维形态,如图8。由图8可知：通过改变速度、距离参数,可实现对安全区模型的三维参数化仿真。水平面可看成是由一个椭圆的变动(大小形状均可改变)而产生,两轴端点在变动过程中保持所在平面与xoy面的平行,垂向边界点分别沿着抛物线方程所确定曲线滑动。对于安全区模型垂向截面,垂向距离与速度有关,安全距离随着速度变化而实时变化,且满足速度越快船舶下沉量越大的结论,与实际相符。由此可见,根据各截面参数计算各个安全区的边界条件,可获得不同速度下船舶安全区的三维分布,以此直观地分析安全区在任意速度下的变化情况,可为LNG船舶安全区模型的精确计算与差异化定量分析提供参考。

图8 不同速度下三维模型模拟效果Fig.8 Simulation effect of 3D model at different speeds

3.2.3 不同模型结果对比分析

结合LNG船舶旋回参数,求该船在航速12 kn时的安全区,并与文献[13-15]的模型(以下简称：FUJII模型[13]、GOODWIN模型[14]和王宁模型[15])进行对比分析,如图9。

图9 与传统船舶领域模型对比Fig.9 Comparison with traditional ship domain models

由图9可知：笔者得出的船舶安全区模型与FUJII模型和王宁模型的形状相近,但比FUJII模型前后纵向距离大,左右横向距离小;比GOODWIN模型和王宁模型的区域要小得多,其结果是符合情理的。同时传统计算方法中LNG船舶的安全区长度均为定值,即船舶安全区长度可描述为n倍的L(n为常数),文中模型考虑了船舶速度大小,结果为非规则几何形状,能反映不同方位上安全区尺度大小。

4 基于安全区模型的会遇仿真

4.1 动态安全区参数

为验证所构建的动态安全区模型在近距离会遇态势下的合理性,笔者使用MATLAB模拟了船舶在会遇场景中的航行过程,实现了仿真结果的实时动态显示。

在两船会遇场景中,设定每个单位格长度为500 m,横轴正向指为正东,纵轴指向正北。对本船而言,本船船长为127 m,船宽为19 m,本船以航向180°,航速12 kn向南正常行驶,发现正前方处同型目标船以航向000°,航速12 kn向本船驶来,初始相对方位为180°,两船相距约3 000 m。

将船速带入安全区数学模型,分别得到本船与目标船初始安全区的4个半轴Rbow、Rstern、Rport、Rstarboard的长度分别为866、866、125、180 m。在航行过程中,本船按照COLREGs要求向右转向,并从目标船的尾部驶过以避让目标船。

以3艘船舶会遇场景为例进行实验。横轴正向指为正东,每个单位格长度为400 m;纵轴指向正北,单位格长度为200 m。本船西向速度是12 kn,1号目标船东向速是4 kn,2号目标船的航行速度为12 kn,初始航向角是045°。以船舶为圆心,运用船舶安全区计算模型进行计算,分别得到不同船舶的安全区边界。

4.2 会遇结果展示及分析

4.2.1 内河航道单船会遇分析

对遇场景的仿真如图10。图10(a)中：1、2号线分别为本船与目标船开始时速度12 kn的安全区,虚线为航线轨迹。本船从起点开始航行,在航行过程中与目标船形成对遇局面,按照内河避碰规则,上下游船舶采取调速、调向等避碰措施,相互未侵入对方的船舶安全区,保障在船舶安全区外完成对遇;在此期间,本船和目标船速度会不断的进行更新,其安全区也一直在变化。3、4号线分别为目标船降速至4 kn和本船降速至10 kn的安全区。船舶因减速而导致舵效变差,此时适当减小船舶安全区长轴、短轴符合船舶航行实际情况。由图10(b)可知：与其他模型相比,笔者的模型提供了较为适宜的安全区域。在这种情况下,目标船从前方驶向本船;随着这两艘船越来越近,不同的船舶安全区被依次侵入。GOODWIN模型是最保守的船域,FUJII模型是风险最大的船域,而笔者模型则提供了适度的区域。

图10 对遇场景的仿真Fig.10 Simulation of encounter scenes

4.2.2 内河航道多船会遇分析

多船对会场景的仿真如图11。图11中：本船从上行航道欲驶向支流,目标船1在支流欲驶向干流,并在干流与目标船2及本船均形成交叉会遇局面,按照内河避碰规则,目标船1为让路船须减速避让,从两船船尾驶过,此时基于建立符合目标船1速度的船舶安全区模型,计算各边界,并得到目标船1的安全区;避让后,目标船1继续航行逐渐加速,随着速度增大,目标船1安全区尺度也相应增大;此时本船与目标船2形成交叉会遇局面,本船为让路船,需从目标船2船尾进行减速避让。这一过程中船舶安全区半径取值既要保证在避碰过程中两侧安全距离及前方安全距离,又需要解决当船速过快而船头安全区过小时为让路船避让时机和避让操作留有时间不足的问题,船舶安全区取值符合内河安全航行要求。从上述过程可看出,这3艘内河船舶在仿真实验中均进行了安全避让,表明笔者所建立的安全区模型能灵活应对内河纷繁复杂的交通会遇情形。

图11 多船对会场景的仿真Fig.11 Simulation of multi-ship meeting scene

5 结 论

笔者从内河LNG船舶航行及操作的特点出发,构建了基于速度特征的三维动态船舶安全区模型,确定了定量计算安全区尺度的方法,得出如下结论：

1)提出了基于速度特征的LNG船舶动态安全区的建模方法,并将安全区由二维平面拓展到了三维空间,其形状和不同方位的尺度都能随着运动的变化而动态自适应,克服了传统模型单一形状且尺寸固定的问题;同时能较好地反映船舶水平航行和水下垂向运动特性,满足内河LNG船舶实际航行的安全需求;

2)内河水域通航环境较为复杂,需要不断调整船舶速度以达到效益与安全的平衡点,而速度变化使得LNG船舶的三维安全区呈现出不断变化特征,动态地确保了船舶在不同方向上的安全距离,为船舶驾驶员的实践中提供了一定的理论参考依据;

3)LNG船舶速度降低时,其舵效较差,航向稳定性较差,同时转向惯性较大,需要提前施加更大的舵角。在LNG船舶加减速混合航行模式下,需要对船舶速度单一变量控制来设置合理的安全区尺度,以保证其他船舶在安全区外航行,同时减少对航道时空资源的消耗,避免对航路上其他船舶造成较大干扰。随着速度改变后,可通过增加巡逻船数量来确保船舶自身及航道整体安全;

4)今后可利用船舶实时AIS数据,基于航行环境、桥区、弯道及特殊航道等参数,进一步优化LNG船舶的安全区模型,实现真实场景下的航行冲突危险度评估。