基于截尾分布的永久路面结构可靠度分析

王国清,张 权,何兆益,秦禄生,邱文利

(1.河北交通投资集团有限公司,河北 石家庄 050091;2.同济大学 道路与交通工程教育部重点实验室,上海 201804;3.重庆交通大学 土木工程学院,重庆 400074)

0 引 言

高速公路在施工和运营过程中存在许多不确定性因素,可靠性问题尤为突出[1]。将可靠度理念引入到路面结构设计和评估中,可实现安全性和经济性的统一[2]。

路面结构可靠度的影响因素主要包括环境、材料、结构组合和交通荷载等,结构力学响应表达式含有不易显式和求偏导的无穷贝塞尔积分函数,因而结构可靠度的计算常以蒙特卡洛模拟为主[3-5]。已有研究中,王昊[6]用蒙特卡洛法分析了基层模量对弯沉和层底拉应力指标可靠度的影响,得到了结构95%可靠度的模量变异范围;裴建中等[2]认为路面结构可靠度的研究在结构失效模式和不确定性参数分析等方面亟需完善;杨聪利[7]结合基层疲劳指标设计了沥青路面结构可靠度软件框架,但该软件还未完善,不能完整参与结构可靠度计算;Huang Wei等[8]分析了交通荷载、结构和材料等参数对沥青路面车辙指标的可靠性影响,建立了车辙可靠性与影响因素的回归模型;付宇[9]结合沥青路面基层疲劳和永久变形两个指标开发了沥青路面结构可靠度计算程序。

已有研究多围绕沥青路面结构弯沉和层底拉应力指标开展可靠度分析,少有在现行规范下对永久性沥青路面结构疲劳等指标的可靠度分析。上述路面可靠度计算模型均采用典型分布的无界抽样,未考虑参数在现实生产中的有界性,计算得到的可靠度与工程实际不符[10-13]。笔者依托河北京德高速半刚性基层永久性沥青路面实际工程,实测与统计相结合,分析了路面结构层厚度、沥青饱和度等参数的变异特性,基于实测数据的“有界”性,将传统结构可靠度计算参数分布的完整分布模式拓展为双截尾分布的形式,并开发了截尾分布下使用Monte Carlo模拟计算路面结构可靠度的程序,评估了京德高速沥青路面结构的可靠性。

1 结构可靠度计算方法

1.1 蒙特卡洛法基本原理

根据JTG 2120—2020《公路工程结构可靠度设计统一标准》,沥青路面结构可靠性定义为：正常设计、施工和使用条件下,路面结构在规定时间和条件下完成预定功能的能力,可靠度为相应的概率。

结构失效概率pf的计算如式(1)：

(1)

式中：D为功能函数g(x)<0的范围,即失效区域。

用于判断结构是否失效的示性函数,如式(2)：

(2)

(3)

1.2 截断随机数的产生方法

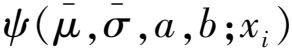
(4)

(5)

设p为[0,1]上服从均匀分布的随机数,则指定范围的正态分布随机数xi产生方式如下：

(6)

(7)

为说明截断方式的适用性,举例如下：若随机变量xi服从均值μ=40,标准差σ=10的正态分布,截尾正态(a=25,b=55)和正态分布条件下随机数的概率密度分布如图1。截尾正态在截断区间外产生随机数的概率为0,因此该方法能产生累积概率密度为1的指定区间分布随机数。

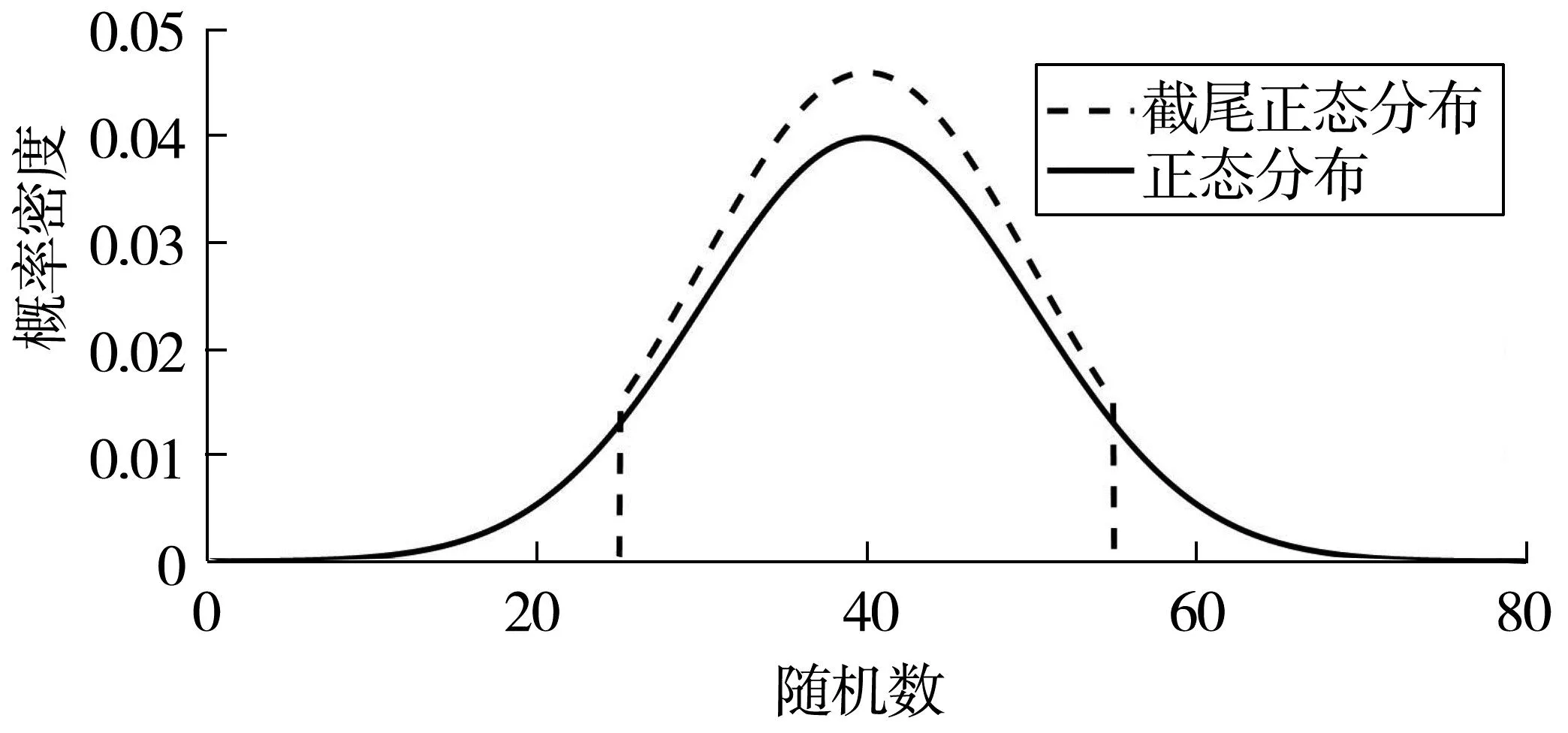
图1 截尾正态和正态的概率密度Fig.1 Probability density of truncated normal and normal

1.3 极限状态功能函数

为计算路面结构可靠度,选取JTG D50—2017《公路沥青路面设计规范》中沥青混合料层疲劳指标、无机结合料稳定层疲劳指标和路基顶面竖向压应变验算指标与交通轴载建立极限状态功能函数如式(8)～式(10)。

沥青混合料层疲劳极限状态功能函数如式(8)：

g1=6.32×1015.96-0.29β×Ka×Kb×KT1-1×(εa)-3.97×(Ea)-1.58×VFA2.72-Ne1

(8)

式中：β为目标可靠指标;Ka为季节性冻土地区调整系数;Kb为疲劳加载模式系数;Ea为沥青混合料20 ℃时的动态压缩模量,MPa;VFA为沥青饱和度,%;KT1为温度调整系数;εa为沥青混合料层层底拉应变;Ne1为设计使用年限车道内面层的累计当量设计轴载数。

无机结合料稳定层疲劳极限状态功能函数如式(9)：

(9)

式中：KT2为温度调整系数;RS无机结合料稳定材料的弯拉强度,MPa ;m,n为疲劳试验回归参数;Kc为现场综合修正系数;σt为无机结合料稳定层层底拉应力,MPa;Ne2为设计使用年限车道内基层的累计当量设计轴载数。

路基顶面竖向压应变极限状态功能函数如式(10)：

g3=1.25×104-0.1β×(KT3×Ne3)-0.21-εz

(10)

式中：Ne3为设计使用年限车道内路基的累计当量轴载数;KT3为温度调整系数;εz为路基顶面竖向压应变。

2 结构可靠度计算方法

2.1 路面施工变异性

路面结构上、中和下面层设计厚度H1、H2、H3分别为4、8、12 cm;水泥稳定碎石上、下和底基层设计厚度H4、H5、H6均为18 cm;中面层设计沥青饱和度VFA为65%。通过跟踪京德高速在建项目,统计了设计指标现场检测数据的均值、上下限和变异系数范围如表1。

表1 路面结构现场参数统计Table 1 Statistical table of on-site parameters of pavement structure

2.2 路基施工变异性

使用动态回弹模量测试仪实测了1 200组京德高速、荣乌新线高速部分标段主线及匝道的路床顶面动态回弹模量样本。其中,京德主线1为：K15+650—K17+320、京德主线2为：K41+900—K43+300、荣乌主线为：K80+580—K81+820、京德主线3为：K96+750—K99+250、荣乌匝道为：AK0+80—AK0+800在路基交工验收时的动态回弹模量均值、区间和变异系数统计结果如图2。

图2 路基动态回弹模量范围Fig.2 Dynamic resilient modulus range of subgrade

3 永久路面结构可靠度的评价

3.1 结构可靠度计算位置

经笔者对永久路面结构的力学计算分析可知：面层、基层和路基的最大力学响应位置分别为中面层底部轮中心,底基层底部两轮中心,路床顶面两轮中心,将以上3个位置作为路面结构可靠度的计算点。各点力学响应随厚度和模量的变化结果由弹性层状体系理论软件计算,通过将拟合的正交回归多项式代入极限状态方程开展可靠度计算。

3.2 路面结构参数

上面层、中面层、下面层、上基层和下基层厚度分别为H1～H5,模量分别为E1～E5。路床模量E0,中面层沥青饱和度VFA和底基层弯拉强度R1等可靠度计算输入参数如表2[14],其中,路面材料泊松比均为0.25,路基土为0.4。

表2 路面结构输入参数的随机特性Table 2 Stochastic characteristics of input parameters of pavement structure

3.3 交通参数

取2021年6—12月,京德高速沿线大兴机场、永清空港、永清花都、霸州东、文安北、文安西、大留镇等7个收费站进站和出站口的2类～11类车的交通数据。将车道系数、方向系数和年平均交通量增长率等参数的变异性考虑在累计当量轴次中,得到40 a使用年限面层、基层和路基的交通量累计当量轴次如表3。

表3 京德高速40年交通量的累计当量轴次Table 3 Cumulative equivalent axle number of traffic volume of Jing-De Expressway in 40 years 107次

3.4 可靠度的分析与评价

为了比较参数有界性模型和参数无界分布模型对结构可靠度的差异影响,结合表2中路面结构参数,笔者分析了荷载应力0.7 MPa、交通量Ne的变异系数为0.8的条件下两种分布模型的计算结果。图3为截尾分布随机变量与无界理论分布随机变量的可靠度程序计算结果。对比分析表明：输入参数边界对结构各层可靠度的影响,随失效概率增大而增大;考虑输入参数的有界性,能有效避免极端和异常变量影响,提高了结构可靠度计算的准确性,可纠正传统方法中可靠度不可能为1的情况,更符合工程实际。

图3 参数有界性对可靠度的影响Fig.3 Influence of parameter boundedness on reliability

3.4.1 面层可靠度计算结果分析

笔者在分析中面层可靠度与累计当量轴次关系时,设累计当量轴次服从正态分布,变异水平为0.8,路面结构输入参数如表2,仅分析变化累计当量轴次均值[14]。笔者选择0.70、0.85、1.00 MPa 3种荷载工况分析轴载对面层可靠度的影响[15],图4展示了面层可靠度随累计当量轴次的变化规律,当Ne1=4.914×107次时,面层可靠度为100%。在不同荷载对应的累计当量轴次失效点后,面层结构可靠度随累计当量轴次的增大迅速降低,3种荷载工况下可靠度降低速率的大小为1 MPa>0.85 MPa>0.7 MPa。

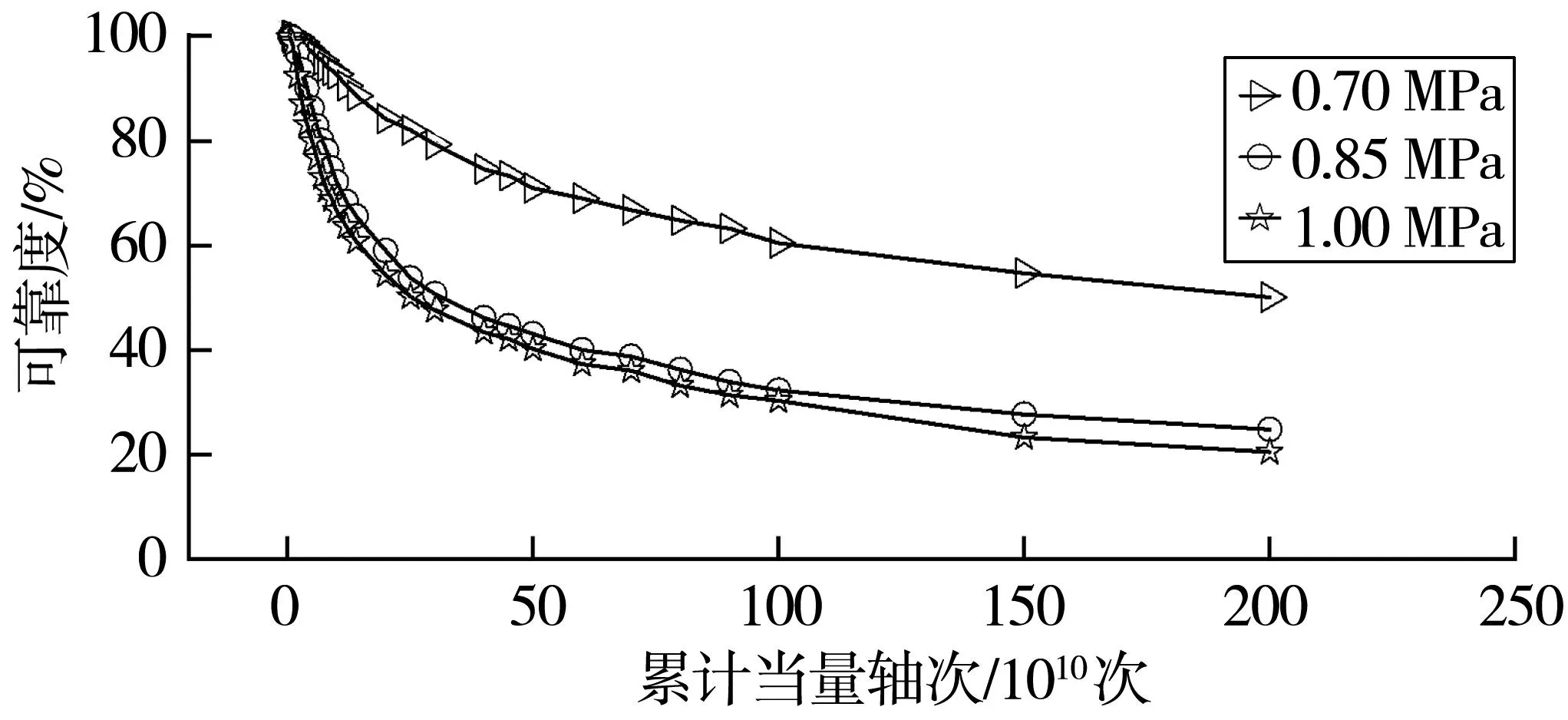
图4 面层可靠度与累计当量轴次的关系Fig.4 The relationship between surface reliability and cumulative equivalent axis number

累计当量轴次在1×1010次～9×1011次时,面层疲劳可靠度降幅明显,说明该区间内可靠度对累计当量轴次敏感系数较高;累计当量轴次大于1×1012次时,可靠度曲线斜率逐渐减小,可靠度降低,说明面层结构在轴载作用下逐渐失效。

3.4.2 基层可靠度计算结果分析

路面结构设计使用年限内,经交通量换算后,基层的累计当量轴次最大,因此基层结构的可靠性能是永久路面结构系统可靠度设计和评估的关键。

基层可靠度主要与累计当量轴次水平及其变异系数有关。标准荷载下,采用响应面法分析基层可靠度Y与不同累计当量轴次A及其变异水平B的变化规律时,路面结构输入参数与面层相同,累计当量轴次的Central Composite Design试验设计水平如表4。

表4 中心组合设计因素和水平Table 4 Factors and levels of central composite design

图5 基层可靠度与A、B的关系Fig.5 Relationship between base course reliability and A,B

图5是A与B对基层可靠度的响应面图。由图5可知：累计当量轴次及其变异系数对基层结构可靠度的影响不一,基层可靠度随着累计当量轴次和变异系数的增大而降低,累计当量轴次对基层结构可靠度的影响大于变异系数。

通过多元回归得到基层可靠度Y与A和B的回归模型如式(11)：

Y=89.997+1.898 45×10-8A+0.063 475B-3.344 76×10-10AB-6.451 9×10-18A2+0.008 856B2+9.474 33×10-20A2B-3.618×10-12AB2R2=99.9%

(11)

由于京德高速是对河北省高速路网的加密,基层累计当量轴次变异水平可为0.1～0.3。计算得到基层可靠度为95.2%～98.7%。符合高速公路和一级公路95%目标可靠度要求。

3.4.2 路基可靠度计算结果分析

分析路基可靠度与荷载应力和累计当量轴次关系时,路面结构输入参数与面层相同。

4种荷载(0.70、0.85、1.00、1.15 MPa)工况下[15],路基可靠度随累计当量轴次的变化规律如图6。其中,1.15、1.00、0.85、0.70 MPa 4种荷载工况对应的累计当量轴次均值失效点分别为：7×1010、8×109、5×109、1×109次,均大于路基使用年限累计当量轴次9.13×107次,即路基结构可靠为100%。在不同荷载应力作用的累计当量轴次失效点后,路基可靠度随累计当量轴次增大迅速降低,4种荷载工况下可靠度降低的大小为1.15 MPa>1.00 MPa>0.85 MPa>0.70 MPa,可靠度曲线斜率先增大后减小,最终趋于0;荷载应力0.70、0.85、1.00、1.15 MPa的敏感区间大致分别为7×1010～5×1011次、8×109～7×1010次、6×109～4×1010次、1×109～3×1010次,该区间内可靠度下降幅度超过50%。

图6 路基可靠度与累计当量轴次的关系Fig.6 Relationship between subgrade reliability and accumulative equivalent axle number

图7为路基可靠度与荷载应力的关系,由图7可知累计当量轴次越大,荷载应力水平越高,路基可靠度越低;累计当量轴次相同时,路基可靠度随荷载应力的增大而逐渐减小。说明路基可靠度与累计当量轴次和荷载应力水平显著相关。

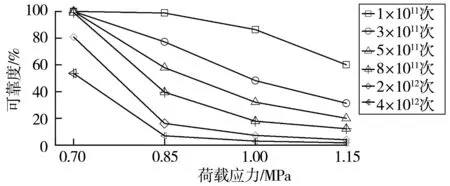
图7 可靠度与荷载应力的关系Fig.7 Relationship between reliability and load stress

4 结 语

基于工程实测数据的“有界性”,通过建立截尾分布下永久路面结构多指标可靠度模型分析了京德高速的可靠度和使用性能规律。结论如下：

1) 考虑输入参数的“有界性”能有效避免极端和异常变量的影响,更符合实际参数的真实分布,不仅提高了可靠度的计算精度,也更准确的反应了结构可靠度的真实情况。

2)京德高速面层疲劳和路基压应变指标的可靠度为100%;累计当量轴次失效点后,面层和路基的可靠度随累计当量轴次增大而迅速降低,下降速率先增大后减小。其中,荷载应力越大,可靠度下降速率越快,累计当量轴次均值的失效点越小。

3) 基层疲劳可靠度为95.2%～98.7%。路面结构基层疲劳寿命的裕度最小;因此,半刚性基层疲劳是永久路面结构设计的关键控制指标。