基于组合深度学习的轨道交通短时进站客流预测模型

李淑庆,李 伟,刘耀鸿,马 波

(重庆交通大学 交通运输学院,重庆 400074)

0 引 言

随着轨道交通的飞速发展,轨道交通网络化运营不断加强,这对轨道交通的运营组织调度、车站管理与服务提出了越来越高的要求。轨道交通短时进站客流是影响车站运营和预警管理与服务水平的重要因素,及时、准确和高精度地对轨道交通短时进站客流进行预测是提高轨道交通系统运行效率、安全、管理水平和服务水平的关键。

目前轨道交通短时客流预测主要分为传统统计模型、机器学习模型、神经网络模型和组合模型等4种方法。传统统计模型主要包括整合移动平均自回归(ARIMA)模型[1]、滑动平均法[2]和卡尔曼滤波[3]等,这类模型计算简单,但无法处理客流序列数据的波动性和非线性关系。机器学习模型主要包括贝叶斯网络[4]、K近邻(KNN)[5]和支持向量回归(SVR)[6]等,这类模型在训练时会消耗大量的内存,无法应用在大样本数据中。神经网络模型主要包括BP神经网络、卷积神经网络(CNN)和长短时记忆神经网络(LSTM)等,惠阳等[7]采用粒子群算法对BP神经网络进行了优化,基于天气、节假日和非节假日等因素对不同站点不同时段的客流进行了预测;MA Xiaolei等[8]将交通流预测定义为图像学习的问题,利用卷积神经网络(CNN)模型对北京二环路和东北的交通网络进行了预测,证明CNN模型可在合理的训练时间内使预测精度提高,适合于对大规模运输网络的预测;YANG Xin等[9]基于客运量历史数据、车站OD矩阵和部分轨道交通网络运营数据,提出了改进的时空长短期记忆模型(SP-LSTM),并用来预测城市轨道交通单个站点的短期出站客运量。这类模型凭借其强大的非线性处理能力被广泛应用于短时交通流预测中,但单个神经网络模型仍存在特征提取不全面而导致预测精度较低的缺陷。部分学者将多种模型进行组合,对轨道交通客流进行了预测。LI Wei等[10]提出了一种结合季节性ARIMA和支持向量机(SVM)的混合模型,该模型结合了单一模型的优势,能很好地对客流数据集下不同形式的关系进行建模;赵阳阳等[11]从历史客流量出发,结合经验模态分解和长短时记忆神经网络的优势,对上海地铁人民广场站进行了预测,结果表明该模型相比传统模型具有更高的预测精度;王秋雯等[12]为进一步提高轨道客流的预测精度,通过K-Means聚类算法实现了客流时段特征的提取,并结合卷积长短时记忆神经网络模型对深圳北站的地铁客流进行了预测。

综上,随着深度学习技术的不断发展,国内外学者将其应用于轨道交通短时客流预测中,并取得了较好效果,但轨道交通短时客流具有很强的非线性和波动性,易受到各种外部因素影响,使得现有模型的特征信息学习因不全面而导致预测精度还不够高、泛化能力还不够强。针对以上问题,笔者基于轨道交通内部客流特性与外部环境因素,结合CNN、ResNet、BiLSTM等3种模型各自的优势,构建了一种多因素的CNN-ResNet-BiLSTM组合模型,并对轨道交通短时进站客流进行了预测。

1 问题描述

轨道交通短时进站客流预测一般是利用历史时间片段信息构造模型,捕捉进站客流内部的复杂关系,对未来某一时段的进站客流量进行预测的方法。

假设t时刻预测的进站客流片段为q[t,t+Δt],预测时间粒度为Δt,令qt=q[t,t+Δt],则有qt=f[(xt-1,xt-2,…,xt-k)T],其中,(xt-1,xt-2,…,xt-k)T表示前k时刻输入的客流影响因素。轨道交通短时进站客流预测问题可转化为寻找一个映射函数g,并使g≈f的过程,这实现了对未来轨道交通各个站点进站客流量的预测。

2 多因素特征变量选取

从轨道交通运营组织调度与预警管理需求而言,以10 min作为轨道交通短时进站客流的预测时间粒度比较合适[13]。影响轨道交通进站客流的因素很多,主要分为内部客流特征和外部环境特征。

2.1 内部客流特征

2.1.1 前序时间客流

当前时刻客流与前序时刻客流具有一定的相关性[14],故选取前10、20、30、40 min的客流作为特征变量。

2.1.2 统计特征

在进行轨道交通短时进站客流预测时,应考虑到进出站客流的影响[15]。对每个站点每10 min和每1 h的客流量进行分组统计,通过分析进出站客流的最大值、最小值和平均值来反映客流的分钟细粒度特征和小时细粒度特征。统计前5 d同一时段的进出站客流最大值、最小值和均值来反映一周工作日的客流特征。

2.1.3 变化特征

利用前3 d进出站客流的平均值,第1、2 d客流的差值,第2、3 d客流的差值,两次变化的差值,第1、2 d的比值,第2、3 d的比值来反映客流变化特征。

2.2 外部环境特征

2.2.1 天气特征

天气变化在一定程度上会对人们出行产生影响,从而导致轨道客流的短期波动[16]。选取能够反映天气与客流关系且易于量化的特征变量作为客流预测的输入变量,如表1。

表1 天气特征变量描述Table 1 Description of weather characteristic variables

2.2.2 空气质量

与天气条件类似,空气质量也会对轨道交通客流产生一定影响[17]。空气质量数据均为数值型变量,将其作为输入特征变量。

2.2.3 道路交通拥堵指数

轨道交通客流与道路交通拥堵指数之间存在一定的相关性[18]。故将道路交通拥堵指数作为输入特征变量。

2.2.4 标记特征

标记每个站点的编号和站点类型,用来反映不同站点的客流特性;将全网的轨道交通站点分为6类,站点类型编号为1～6[19]。为反映客流的时间特性,标记当月的日期范围、对应的周日、轨道运营小时区间。

3 CNN-ResNet-BiLSTM组合模型

3.1 卷积神经网络模型(CNN)

卷积神经网络(convolution neural network,CNN)是深度学习中比较经典的模型,其思想源于模拟自然生物的视觉系统,近年来在图像分类和目标检测方面得到了很好应用[20]。CNN在传统神经网络基础上增加了卷积层和池化层,通过局部连接和权重共享方式,使其能对输入特征进行高效提取,其结构如图1。

图1 卷积神经网络结构Fig.1 CNN structure

CNN中每个位置的特征数据都可与同一卷积核的权值参数进行计算,这与传统神经网络中每个权值参数只能计算一次不同。权值共享不仅极大地减少了参数数量,还充分挖掘了特征局部相关性,通过卷积操作自动提取了相应特征,提高了模型的学习效率。

3.2 残差神经网络(ResNet)

网络模型的性能往往与其深度有关,一般情况下,只要提供足够的训练数据,随着网络结构深度增加,模型的预测效果就会越来越好;但当网络结构深度达到一定程度时,继续增加网络结构,模型则会出现泛化能力减弱的情况,这说明网络结构深度对预测结果影响较大。HE Kaiming等[21]提出了一种新的网络结构,即残差神经网络(ResNet),该网络在普通的堆叠卷积操作外,引入了一个“快捷连接”,将输入张量x直接传送到输出张量中,实现了恒等变换,其结构如图2。

图2 残差模块网络结构Fig.2 ResNet structure

由图2可知：假设神经网络的输入张量为x,期望输出为H(x),原来的神经网络层操作变换为f(x),则残差模块计算输出可表示为H(x)=f(x)+x。如将f(x)的相关参数设为0,即f(x)=0,此时只有“快捷连接”的输入张量x能通过,原来神经网络层中的操作都被屏蔽,这样残差模块就实现了恒等变换。残差模块计算如式(1)：

y=w2σ1(w1x)+x

(1)

式中：y为残差模块输出张量;w2为第2个权重层的权重参数;σ1为ReLU激活函数;w1为第1个权重层的权重参数。

对原始残差网络进行改进,将原本残差网络中Addition层后的ReLU层放在右侧分支层,将批归一化层放在ReLU层前面,并对权重层进行预激活,证明了改进后残差网络的有效性[22],如图3。

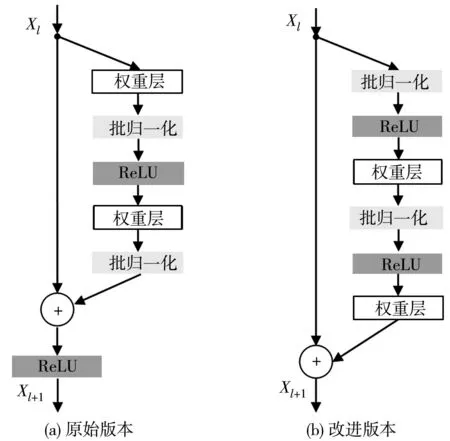
图3 残差模块原始版本与改进版本对比Fig.3 Comparison diagram of original version and improved version of ResNet model

改进后的残差模块使用批归一化可提高模型的正则化,从而减少了过拟合风险,更有利于训练,泛化能力也更强;改进后的残差模块梯度传播更加顺畅,减少了信息流失。

3.3 双向LSTM模型(BiLSTM)

长短时记忆神经网络(long short-term memory,LSTM)是循环神经网络(RNN)的一种变体形式,可适用于轨道交通短时客流时间序列预测。该模型是在RNN基础上添加了门控制单元,能对历史信息进行选择性记忆或遗忘,将重要信息记录下来,遗忘掉价值不大的信息,这种方式能很好地维持模型对输入数据的长期记忆,并在一定程度上解决了RNN只有短期记忆的问题[23]。

LSTM虽可很好地进行时间序列预测,但只能从轨道交通客流单一方向进行数据特征学习。为了提高轨道交通客流预测准确性,笔者采用双向长短时记忆神经网络模型(BiLSTM)对客流数据的时间特征进行提取。LSTM由正、反向模型组合而成[24],其结构如图4。

图4 BiLSTM网络结构Fig.4 BiLSTM structure

(2)

式中：⨁为整合操作。

3.4 CNN-ResNet-BiLSTM组合模型

CNN能从复杂数据中自动提取多维度特征,但不能很好地处理时间序列数据;LSTM能很好地捕捉时间序列数据中的长期依赖信息,但只能从单一方向进行特征学习,没有充分考虑到轨道交通客流前后方向信息对当前状态影响;BiLSTM模型将两个LSTM模型结合,从前后两个方向捕捉了轨道交通客流序列的时间特征,但在处理长时间多维度特征时会存在信息丢失、挖掘不充分而导致预测精度较低的问题;ResNet可缓解因模型层数增加而出现的梯度消失或梯度爆炸问题。基于此,笔者综合上述3类深度学习模型优点,结合轨道交通内部客流特征与外部环境特征,将这3类进行组合,提出了CNN-ResNet-BiLSTM组合模型(以下简称：C-R-B组合模型),如图5。

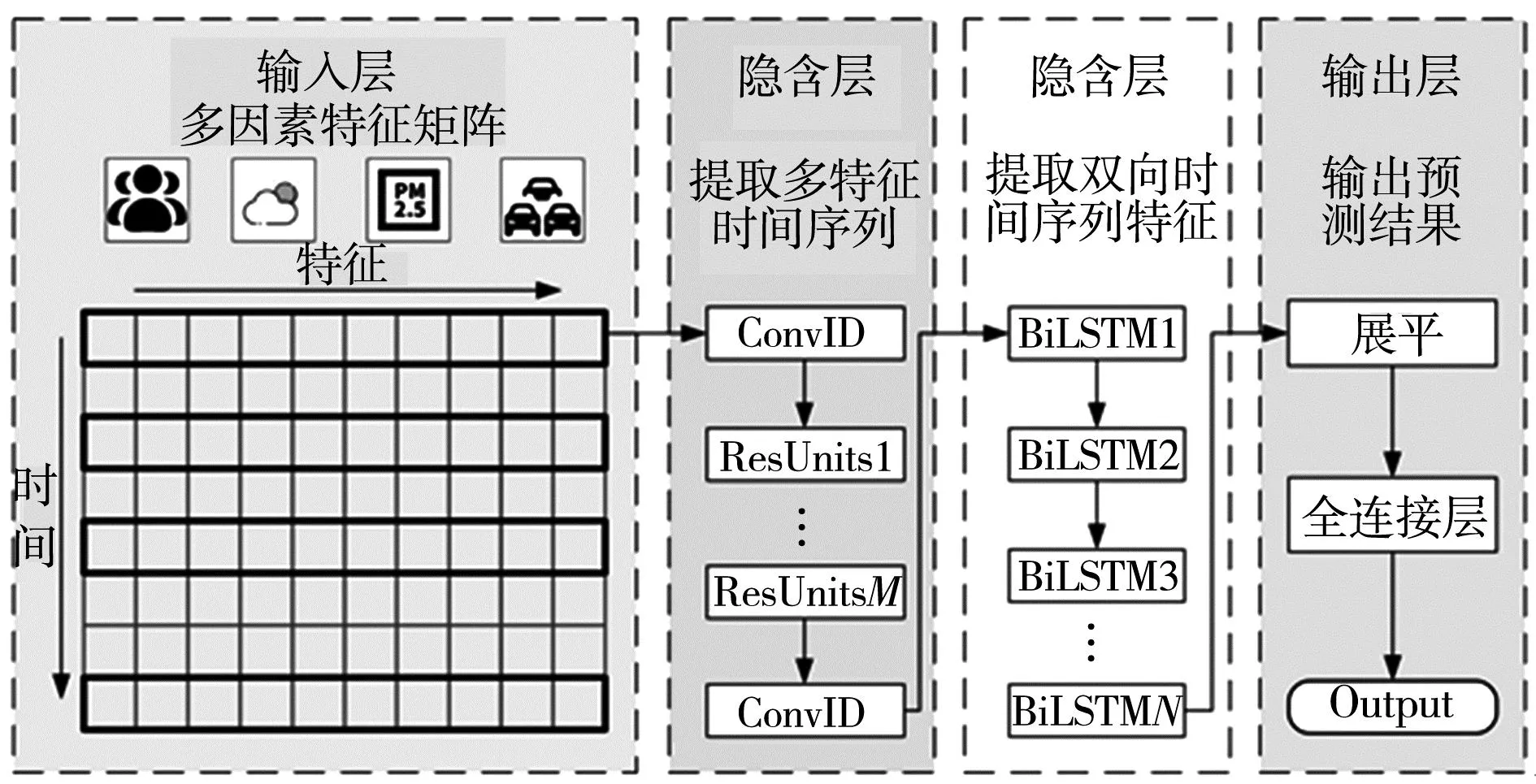
图5 多因素CNN-ResNet-BiLSTM组合模型结构Fig.5 Structure diagram of multi-factor CNN-ResNet-BiLSTM combined model

由图5可知：多因素C-R-B组合模型结构由输入层、隐含层和输出层构成。在输入层中,融合了包括前序时间客流、统计客流及变化客流的内部客流特征因素和包括天气、空气质量、道路交通拥堵指数及标记特征的外部环境特征,并按时间、站点编号顺序构造输入的多因素特征矩阵。在第1个隐含层中,利用CNN中的卷积、池化操作提取多因素客流时间序列特征,减少时间序列数据长度,降低后续网络分析的难度;在CNN中加入残差网络ResNet,以加深网络结构的深度,提高模型的预测效果;在第2个隐含层中,将CNN提取到的特征输入到BiLSTM中,完成前后两个方向的时间序列特征提取;在输出层中,将BiLSTM提取到最终特征进行展平,接入到全连接层,得到最后客流的预测输出值。

3.5 模型训练流程

多因素C-R-B组合模型的训练流程分为8个步骤：

1)选取特征变量构造多因素的轨道交通客流特征矩阵,将其归一化后划分为训练集和测试集;

2)设定模型的批处理大小、模型层数、神经元数及学习率下降策略;

3)初始化多因素C-R-B组合模型的所有权重参数;

4)搭建多因素C-R-B组合模型;

5)计算模型在正向传播网络层中每个神经元的输出值与真实值的误差;

6)将正向传播的输出误差反向传播,计算其误差项以确定每个参数的梯度,利用优化算法对权重参数进行更新;

7)当梯度误差达到要求或者迭代次数达到设定值时,完成本轮训练,否则继续迭代;

8)当模型达到最大训练次数时,输出多因素C-R-B组合模型的预测结果,计算评价指标,保存模型。

3.6 评价指标

选取常用的均方根误差(ERMS)、平均绝对误差(EMA)和平均绝对百分比误差(EMAP)等3个指标来衡量模型的预测精度,其计算为：

(3)

(4)

(5)

4 实证分析

4.1 数据集及实验环境

笔者选用2019年1月2日—26日杭州地铁全网80个轨道站点的刷卡数据(合计7 000多万条)进行分析;选取2019年1月2日—23日的工作日数据作为训练集,1月24、25日工作日的数据作为验证集,训练集、验证集数据比例为8∶1,统计时间粒度为10 min。

硬件环境为Intel(R) Core(TM) I7-9750H CPU和NVIDIA GTX 1660Ti GPU的Windows10 64位操作系统,开发语言为Python,编辑器为Pycharm,利用Tensor-Flow的高级API-keras搭建深度学习网络。

4.2 模型参数设定

采用网格搜索法对批处理大小、模型层数和神经元数进行调节。经反复调参后,得到了多因素C-R-B组合模型的最终优化参数。其中：ResNet网络的层数为3,神经元数均为32;BiLSTM网络层数为1,神经元数为64;设定初始学习率为0.001,当迭代8次模型效果不再提升时,降低学习率;采用Dropout为0.2来避免模型训练过程中过拟合发生。

4.3 不同类型站点预测结果

为评估模型对不同类别站点进站客流的预测性能,将训练好的多因素C-R-B组合模型分别对不同类型站点进站客流进行预测,如图6。

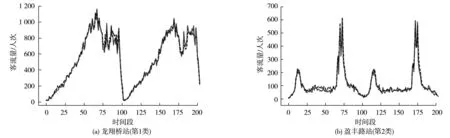
图6 不同类型站点进站客流预测结果Fig.6 Prediction results of inbound passenger flow at different types of stations

由图6可知：即便轨道交通进站客流真实值具有一定波动性,笔者所建立模型仍可精准地捕捉到短时进站客流变化情况,预测效果良好。

4.4 不同模型预测对比

为验证笔者所构建的模型准确性和有效性,选取8个常用的模型与文中构建模型进行对比,其中CNN、LSTM、BiLSTM、CNN-LSTM、CNN-ResNet-LSTM和单因素C-R-B模型的配置参数值与文中构建模型一致。基于评价指标对各个模型预测误差进行计算,结果如表2、表3。

表2 不同模型预测误差Table 2 Prediction error of different models

表3 误差损失值下降百分比Table 3 Percentage decrease in error loss value %

由表2可知：多因素C-R-B组合模型的各指标均优于常用模型,各误差指标均最小。其中：ERMS=21.909 63,EMA=12.884 94,EMAP=12.777 37%。

由表3可知：对比ARIMA、SVR、CNN、LSTM和BiLSTM模型,多因素C-R-B组合模型的ERMS相比单一模型分别降低了34.71%、36.12%、15.92%、16.87%和10.61%;EMA分别降低了43.26%、36.23%、20.63%、17.35%和15.63%;EMAP分别降低了47.23%、38.73%、17.20%、12.18%和17.57%。

在常用单一模型中,深度学习模型的预测表现远远优于传统统计模型ARIMA和机器学习模型SVR。其中,ARIMA预测表现最差,无法很好地捕捉轨道客流非线性,而SVR在建模时消耗大量计算时间,不适用于大型数据集建模。在单一深度学习模型中,具有处理时间序列数据能力的LSTM效果优于CNN型,而BiLSTM效果要优于单向的LSTM,这是因为BiLSTM能同时处理前后两个方向的时间序列数据。然而,单一模型只能学习到单个模型特征,无法结合其他模型优势而导致预测精度较低。

由表3可知：对比CNN-LSTM和CNN-ResNet-LSTM模型,多因素C-R-B模型的ERMS比常用组合模型分别降低了9.24%和8.50%;EMA分别降低了10.00%和6.76%,EMAP分别降低了10.14%和6.52%。

在4个组合模型与5个单一模型对比方面,4个组合模型的3个评价指标均低于常用单一模型,这说明组合模型能结合单一模型优势,提高轨道交通短时进站客流的预测精度。然而对于常用的组合模型,CNN-LSTM只能提取浅层的空间特征信息,CNN-ResNet-LSTM虽能提取深层空间特征信息,但也只能提取到单向的时间序列信息,无法捕捉轨道交通客流的双向时间信息。

多因素C-R-B组合模型相比单因素C-R-B模型的ERMS、EMA和EMAP分别降低了11.74%、6.74%和30.13%。这说明增加的天气、空气质量和道路交通拥堵指数等外部环境因素能提高模型的预测精度,这是因为引入的外部环境因素使模型学习到了更多特征,验证了文中模型引入多因素特征的有效性。

5 结 论

通过融入内部客流特征和外部环境特征多因素,笔者提出了多因素C-R-B组合模型,并对轨道交通短时进站客流进行预测。得出主要结论如下：

1)结合了CNN模型能对多因素客流时间序列的自动提取,ResNet模型能对更深网络结构的高效训练,BiLSTM模型能对客流时间序列的长期依赖,提出了多因素组合模型,实现了对客流时间序列特征的有效提取;

2)除考虑内部客流特征外,还引入了天气、空气质量和道路交通拥堵指数等外部环境因素,通过实例验证了引入多因素特征的有效性;

3)多因素C-R-B组合模型的ERMS、EMA和EMAP值相比于常用的几种模型分别降低了8.50%～36.12%、6.74%～43.26%和6.52%～47.23%,表现出更加准确的预测结果;

4)笔者仅对常规条件下的轨道交通短时进站客流进行了预测,下一步可考虑对节假日、大型活动或突发事件等特殊情况下的轨道交通短时进站客流进行预测,并寻找更多更新数据集对模型进行验证。