基于自适应A*算法的自动驾驶车辆路径规划方法研究

张 涌,成海飞,赵奉奎

(南京林业大学 汽车与交通工程学院,江苏 南京 210037)

0 引 言

路径规划是自动驾驶车辆自主完成导航任务的重要环节和关键技术之一,也是实现完全自动驾驶的核心难题[1]。它的目的主要是根据已知或者未知障碍物的地图环境与所需的约束条件,寻找到一条从起点到终点的最优或次优的安全路径。在自动驾驶车辆路径规划领域,众多学者对算法的开发与探索展开了大量研究,主要包括基于采样的快速搜索随机树方法[2]、Voronoi图方法等,基于节点的Dijkstra算法、A*算法,基于模型的人工势场法[3]、动态窗口法等,以及基于生物启发式的神经网络算法、遗传算法[4]等。

A*算法作为一种启发式搜索算法,节点的拓展具备一定的方向性,且计算量小,被广泛应用于全局路径规划算法,但传统的A*算法存在搜索效率低、拐点数量较多和转折角度较大等问题[5-7]。针对传统A*算法的这些问题,许多学者针对性地进行了相关研究。姜媛媛等[6]利用垂距限值法快速删除搜索路径中存在的冗余节点,并通过B样条曲线平滑拟合出一条光滑的曲线,仿真实验表明该改进算法缩短了运算时间和减少了路径长度;吴鹏等[7]采用目标正反向搜索交替机制使两路径的最终节点在起点和终点连线的中点邻域相遇,提高了搜索效率;王维等[8]通过考虑当前节点与其父节点的估计代价并采用指数衰减的方式对估价函数进行加权、五次多项式平滑处理的方法使规划路径可以在复杂环境下可以可靠地到达目标;孔慧芳等[9]采用加权曼哈顿距离与转弯修正代价作为新的启发函数,改进的算法可以有效减少AGV路径规划时的节点遍历数与转弯次数;张建光等[10]在四节点扩展方式的基础优先考虑目标点方位的相邻节点,并在估价函数中添加略大于1的权重因子与拐点处转弯代价,使生成的路径能有效的减少搜索节点数目以及搜寻路径的转弯次数;孟珠李等[11]将传统A*算法得到的路径作为控制点,并利用3次B样条插值使路径尖峰处得到优化,并生成一条平滑的曲线,使得农用机器人运行更加顺畅;田海波等[12]通过在估价函数中考虑转弯成本、预判断规划策略、冗余拐点剔除策略3个方面对传统A*算法进行优化处理,使生成的路径长度缩短,拐点数量减少,转折角变小。上述研究通过节点扩展、平滑处理等方法优化了路径,但是并没有综合考虑得到的路径是否符合自动驾驶车辆的实际运动约束。

为了解决上述问题,针对A*算法计算时间较长的问题,笔者采用指数增长法对启发式函数进行加权,从而提高搜索效率。考虑自动驾驶车辆在实际运行过程中自身转向特性的限制,得到长度更短、转折角度更小的路径。此外,采用三次B样条曲线对生成路径的拐点处进行平滑处理,使路径具有连续的曲率,有利于自动驾驶车辆的控制。仿真结果表明：与传统A*算法相比,改进的A*算法生成的路径长度明显缩短,总航向角更小,路径更加平滑。

1 算法描述

1.1 环境建模描述

自动驾驶车辆进行路径规划前,须根据传感器感知的环境信息进行地图模型搭建。目前,使用最多的地图种类有3种：可视地图、栅格地图、拓扑地图。其中,栅格地图由于自身模型易构建以及位置表示的唯一性等优点,在路径规划时被广泛采用,因此笔者将采用栅格法来构建地图。

在栅格地图上构建障碍物时,为保证环境信息的真实性,通常将障碍物的原始形状作为首要选择,此方法会导致障碍物的边缘失真,从而影响路线的可追溯性和安全性。现有的研究大多采用矩形封闭障碍物的原始形状的方法来避免边缘局部失真[14]。同样应用文献[13]所提及的障碍物处理办法,地图环境中的障碍物形状统一用矩形表征,图1为利用矩形代替圆形和不规则五边形的实际外形。由图1可以看出,此时原障碍物的安全性问题转化为矩形障碍物的安全性问题。

图1 障碍物代替示意Fig.1 Schematic diagram of obstacle replacement

静态全局环境下,栅格地图实例如图2,左下角栅格为起点,右上角栅格为终点,空白栅格表示自动驾驶车辆可以通过(可通行区域);黑色栅格表示不可通行的障碍物(不可通行区域)。

图2 栅格地图实例Fig.2 Grid map example

1.2 传统A*算法

A*算法是一种经典启发式搜索算法,在Dijkstra算法和BFS算法基础上,结合二者的优点,通过启发式搜索,利用代价函数作为寻路依据,避免了搜索过程中方向的盲目性,从而获取最优路径。A*算法的基本思想是将起始点S作为第1个父节点添加至Open list列表中,利用代价函数估值从父节点到周围节点n的价值,选择最小的节点作为下一个父节点,直至搜索到目标节点G并且将目标节点G添加至Close list列表为止。启发函数由两部分组成,如式(1)：

f(n)=g(n)+h(n)

(1)

式中：f(n)为起始节点S到目标节点G的路径总代价;g(n)为从起始点S到当前点n的实际代价;h(n)为当前节点n到目标节点G的预估距高。

一般地,计算h(n)的典型距离计算公式有曼哈顿距离、欧几里得距离、切比雪夫距离,对应表达式分别如式(2)～式(4)：

h(n)=|xn-xm|+|yn-ym|

(2)

(3)

h(n)=max(|xn-xm|,|yn-ym|)

(4)

对比3种距离运算公式且基于行走规则,式(2)的曼哈顿距离运算简单,搜索效率高,但其运动方向只允许朝上下左右4个方向移动导致生成的路径质量偏低;式(3)的欧几里得距离易求得最短路径,且可使自动驾驶车辆朝任何方向移动,但计算时必须先平方和后开根,造成搜索效率低;式(4)的切比雪夫距离在进行估值运算时与最优路径的估值误差不大,但在斜向搜索时会低估距离(没有考虑斜向路径的实际长度且路径规划过程中允许朝8个方向移动,以车辆所处位置为中心单元,在3×3邻域里,八方向指的是前、后、左、右、左前、左后、右前、右后)。自动驾驶车辆完成驾驶任务过程时,运动方向是任意的且使用欧几里得距离更逼近实际驾驶过程,所以笔者使用欧几里得距离公式计算h(n)的值。

2 A*算法改进

传统A*算法及文献[11]的改进A*算法在任意地图中自适应性较差,在路径规划时存在遍历节点数多、总转折角度大、规划路径不够平滑、寻路时间较长等问题。综合文献[11]所提改进思路,在设计思路时需要避免出现因提高某一方面性能指标导致其他性能降低的情况。通过设计自适应调整权重因子、转弯成本函数(航向角影响因子)、路径平滑处理方式来改进A*算法,保证最终规划出的路径相对最优,提高算法的鲁棒性和搜索效率,减少拐点数和总航向角。

2.1 启发函数自适应权重因子

A*算法的预估代价函数是影响算法效率的重要因素,h(n)的值越接近实际值,搜索的效率就越高。若h(n)=0时,A*算法退化为Dijkstra算法,此时算法可以在全局范围内搜索到一条最短的路径,但是需要遍历所有节点,搜索效率以及时间成本会大大增加。若h(n)>>g(n)时,启发函数中g(n)的作用可忽略不计,此刻A*算法会演变成为 BFS算法,该算法严格遵守最短距离扩展节点,但这仅仅保证了相对最优的路径,而不是最优选择。综上,笔者在启发函数的预估代价部分引入自适应权重因子w,则原算法公式中的h(n)就变成了w×h(n),由此式(1)可表示为：

f(n)=g(n)+w×h(n)

(5)

(6)

w的引入可以为h(n)带来更大的权重。自适应权重因子w的值取决于从起始节点S到当前节点n的实际代价与从当前节点n到目标节点G的预估代价的比值(呈正比例关系)。在改进的A*算法的执行过程中,需要收集实时的数据,启发函数中的动态调整自适应权重因子w的g(n)/h(n)部分会随着路径搜索进程的变化而不断更新取值,使得算法更加注重平衡搜索效率和路径质量。具体来说,如果当前搜索节点与起点距离较近,那么改进的A*算法会更加注重搜索效率,从而在搜索过程中更加注重速度;如果当前搜索节点与起点距离较远,那么改进的A*算法会更加重视启发式函数,从而在搜索过程中更加注重路径质量。

同时,为保证路径搜索时间w≥1,笔者在g(n)/h(n)的基础上引入以e为底的指数函数。因此在路径搜索初期,w的值较小,可以通过增强算法的发散性达到扩大路径搜索范围的目的;路径搜索后期,w的值较大,可以通过增强算法快速收敛的性能以提高路径搜索的效率。

2.2 考虑航向角影响因子的启发函数

路径规划时,由于障碍物的分布与最短路径效应,会使规划生成的路径有较多转折点数量且出现较大转折角的情况,对应地,自动驾驶车辆在转弯过程中会出现先减速后加速的情况,通过转弯所花费的时间代价相对来说比直线行驶高,从而使得整体的效率下降,而且生成的路径质量无法得到保证。因此,将航向角成本也考虑进A*算法的启发函数信息中,使自动驾驶车辆尽可能选择满足其自身转弯特性的路径。要控制自动驾驶车辆的运动,就必须建立准确的车辆运动数学模型,此模型不仅需要真实反映车辆的某些特性,还应该尽可能地简单易用。所以,对自动驾驶车辆模型简化,将自动驾驶车辆作为一个整体,只考虑航向角对全局路径规划的影响,因此,得到其简化模型如图3。

图3 某一时刻自动驾驶车辆航迹Fig.3 The track of the autonomous vehicle at a certain moment

自动驾驶车辆运动时,位置由节点A→B→C的变化过程中,为了方便计算与更好地描述,在惯性坐标系XOY下,对以下坐标点假设：父节点前一节点A(n0,m0),子节点C(nn,mn),子节点C的父节点B(nn-1,mn-1),ΔL为节点A到节点C的直线距离。故自动驾驶车辆的航向角的表达式可以写成如下：

(7)

α=arccosb

(8)

(9)

式中：α为自动驾驶车辆某时刻运动状态的航向角;d为α转换为弧度制下的值。考虑到车辆本身的最大转向角度限制。在自适应权重因子的A*算法启发函数的基础上添加航向角影响因子q,其中,q为自动驾驶车辆在进行转向时因航向角变化而引起的代价。其运算公式如式(10)：

q=d

(10)

综上所述,改进后的A*算法的启发函数如式(11)：

f(n)=g(n)+w×h(n)+q

(11)

2.3 B样条算法光滑处理

A*算法规划出来的路径是由一些有向线段组成的,虽然笔者提出的改进方法在一定程度上优化了转折角过大的问题,但是在某两线段的转折点,如图4的(9.5,15.5)处,路径比较尖锐,此时会因为运动方向突变使自动驾驶车辆的安全性得不到保证。因此笔者将采用B样条算法,以产生出连续、平滑的路径曲线。

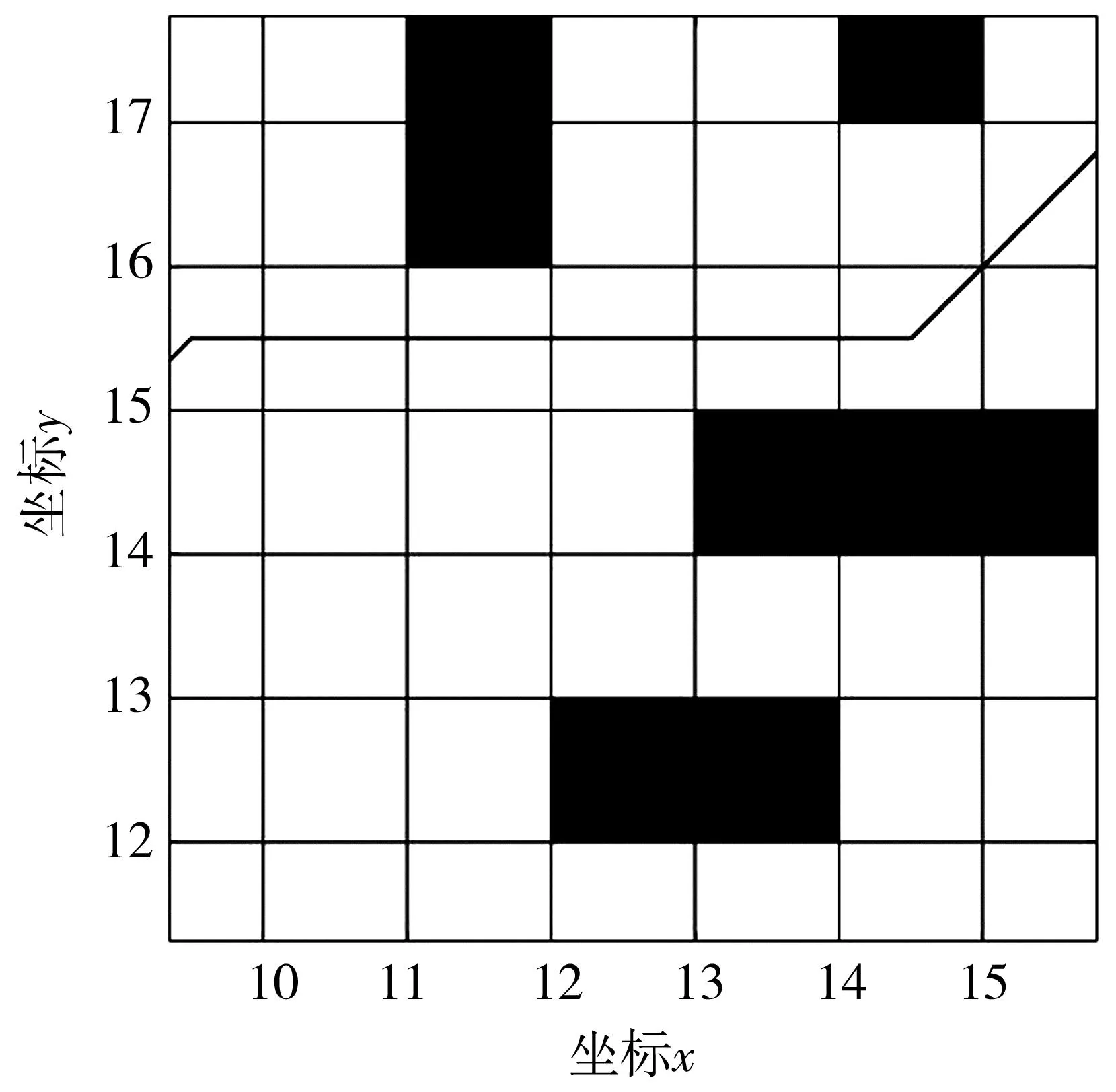
图4 考虑自适应调整权重因子与航向角影响因子时某段生成的路径Fig.4 The path generated by a certain segment considering the adaptive adjustment of the weight factor and the heading angle influence factor

B样条算法的优点为曲线会落在曲线阶数的控制点所形成的凸多边形内。3次B样条算法在节点连接处二阶连续,应用于路径规划时,可以满足自动驾驶车辆速度和加速度连续性的要求,因此笔者采用3次B样条算法来平滑A*算法已规划出路径[14]。

k次B样条算法的数学表达式为：

(12)

式中：Pi为控制转折点i的坐标;Fi,k(t)为k次B样条的基函数,其表达式为：

(13)

(14)

由式(12)、式(13)可得3次B样条曲线的基函数数学表达式

(15)

将式(15)代入式(12)可得：

P(t)=[(-C0+3C1-3C2+C3)t3+(3C0-6C1+3C2)t2+(-3C0+3C2)t+(C0+4C1+C2)]/6

(16)

将式(16)用矩阵形式表达为：

(17)

式中：t∈[0,1]。

3 仿真结果和分析

为验证改进A*算法的有效性和灵活性,笔者在2组不同的环境下进行了仿真试验,仿真软件平台为MATLAB R2019a,硬件平台为Intel Core i5-10200H 2.40GHz CPU,RAM 16 GB。

为保证笔者所提出算法的可靠性与优越性,设置了20×20、30×30和50×50的3组栅格地图进行仿真验证,最小栅格大小为1 m×1 m。每组地图分别应用传统A*算法、文献[11]的改进A*算法(BA*算法)、自适应权重因子A*算法(WBA*算法)与最终改进A*算法(AWBA*算法)。其中,BA*算法是一种基于A*算法的路径规划算法,通过引入B样条平滑技术来提高路径的平滑度;WBA*算法是在传统A*算法的基础上进行改进的搜索算法,它考虑了自适应权重因子和3次B样条平滑处理方法;AWBA*算法是在WBA*算法的基础上进一步改进的搜索算法,它引入了航向角影响因子来更好地适应具有方向性的问题。构建的栅格地图和传统 A*算法路径规划仿真结果如图5(a)、图6(a)与图7(a)。

图5 20×20栅格地图路径规划Fig.5 20×20 raster map path planning

图6 30×30栅格地图路径规划Fig.6 30×30 raster map path planning

在文献[11]中,利用3次B样条算法对传统A*算法规划出的路径进行了平滑处理,并设计了相关系统验证了此算法的可行性,即优化后的光滑路径可以使农用机器人顺畅运行。相比于BA*算法,AWBA*算法虽然在搜索时间方面没有较大提升,但是在路径长度与总航向角等方面的提升较大。

表1比较了3种不同地图环境中4种算法的性能指标。结合表1、图5(c)图6(c)与图7(c)可以看出,20×20、30×30与50×50的3组栅格地图中,WBA*算法相较于传统A*算法路径长度分别减了5.48%、6.33%、9.03%,搜索时间缩短了21.43%、23.73%、7.59%,总航向角减少了1.83%、0.18%、12.57%。搜索时间的显著减少,表明WBA*算法更高效,可以在更短的时间内完成路径搜索。

图7 50×50栅格地图路径规划Fig.7 50×50 raster map path planning

20×20的栅格地图环境中,AWBA*较传统A*算法相比,生成的路径长度缩短了11.14 %,总航向角减小了2.15%,搜索时间无明显变化,但是拐点数量较于传统A*算法略增。30×30的栅格地图环境中,AWBA*较传统A*算法规划出的路径长度缩短了7.34 %,拐点数量减少了42.86%,总航向角减少了1.17%,搜索时间缩短了8.47%。50×50的栅格地图环境中,AWBA*算法较传统A*算法规划出的路径长度缩短了18.64%,拐点数量减少了66.67%,总航向角减少了23.08%,搜索时间缩短了2.07%。

表1 4种算法性能指标对比Table 1 Comparison of performance indicators of four kinds of algorithms

仿真结果表明：20×20的栅格地图环境下,WBA*算法和AWBA*算法生成的路径拐点数量相较于传统A*算法略增,说明算法在搜索过程中使用了更多的信息,需要优化除了路径长度之外的其他目标,如航向角影响因子等,导致算法选择一条拐点数量略增的路径,以满足这些优化目标。传统A*算法预估代价函数不准确可能会找到次优解,但是WBA*算法和AWBA*算法一定程度上克服了预估代价函数的不准确性,导致搜索得到的路径长度更短。在30×30与50×50的栅格地图环境,WBA*算法和AWBA*算法生成的路径拐点数量明显少于传统A*算法,其他指标也均优于传统A*算法与BA*算法,说明WBA*算法和AWBA*算法都能够适应复杂的地图环境并保持其可行性和优越性。

综合评估,地图环境愈加复杂,AWBA*算法虽然搜索时间并没有太大的提升,但路径长度明显缩短、总航向角减少,并在生成路径的基础上使用3次B样条算法对拐点处进行平滑处理,使最终路径更适合自动驾驶车辆运动的特性。

4 结 语

针对传统 A*算法在路径规划中存在的不足,提出了具有自适应调整权重因子、考虑航向角影响因子的启发函数、路径平滑处理的改进A*算法。该算法通过指数增长法使启发函数中的估价函数随路径变化提高搜索效率;随后在启发函数中考虑转弯所带来的影响(航向角影响因子),使自动驾驶车辆满足其基本的转向特性;最后利用3次B样条算法平滑处理生成的路径。通过仿真对比分析,提出的改进A*算法在愈加复杂的环境下拐点数更少、路径更为平滑、路径距离更短,证明了所提算法的优越性和可行性。接下来将结合其他智能算法,研究如何在动态环境中快速准确地规划出自动驾驶车辆最优路径。