腐蚀作用下城市轨道车辆齿轮磨损可靠性研究

徐向阳,陈庆科,王 晗,任梓源

(重庆交通大学 机电与车辆工程学院,重庆 400074)

0 引 言

齿轮磨损现象广泛存在于城市轨道车辆齿轮传动系统中,随着设备服役寿命增加,磨损量不断累积,会改变齿形轮廓和载荷分布[1],降低传动精度,导致齿轮啮合过程中产生异常振动和噪声,形成“软失效”[2]。过度磨损会提高齿轮的“硬失效”概率(如轮齿断裂和齿面胶合),严重降低齿轮系统的可靠性。以磨损深度作为关键参数,量化齿轮的磨损可靠性,随着磨损深度增加可靠性降低,当齿面最大磨损深度达到阈值时,定义为齿轮失效[3]。

重庆位于长江以及嘉陵江的汇合处,水汽充沛,空气湿度高[4]且含有强氧化性的阴离子[5]。随着轨道交通传动系统齿轮箱的“呼吸”作用,潮湿空气会进入齿轮箱内部,导致齿轮表面发生电偶腐蚀[6],形成微小腐蚀凹坑,进一步促进齿面磨损。因此,开展腐蚀作用下的齿轮磨损可靠性研究具有重要意义。

通过将齿轮磨损过程视为随机过程并基于Archard磨损模型进行齿轮磨损可靠性研究。PEI Jiaxing 等[3]将齿轮磨损失效定义为最大磨损点的磨损深度超过特定阈值,齿轮磨损的可靠性问题可看作一个首通问题,可采用马尔可夫扩散过程描述齿轮磨损深度;YUAN Zhe等[7]认为影响磨损量的因素众多,且呈现非线性关系,具有明显的随机性和时变性;ZHAO Fuqiong等[8]采用贝叶斯后验定理,将齿轮磨损系数的先验分布分别考虑为高斯分布和均匀分布,将不同时刻的实验数据进行贝叶斯更新,更新后的磨损系数更接近真实值。针对电偶腐蚀现象,CUI Chuanjie等[9]通过对材料表面腐蚀坑的数目与深度进行统计,建立了相应的数学模型;王晓敏等[10]考虑载荷效应过程及失效模式间的相关性,提出了一种预测受腐蚀影响的地下钢管系统失效概率方法;李牧等[11]认为腐蚀虽然对材料性能影响有限,但会对结构产生较大影响,因此将均匀腐蚀对系泊系统可靠性的影响,简化为腐蚀作用使锚链截面面积的缩小进而导致可靠性降低;董彬杰等[12]通过对系泊链钢在人工海水条件下的腐蚀磨损进行试验,发现腐蚀与磨损的交互作用主要体现在腐蚀对磨损的促进。可见,腐蚀作用对磨损的促进不可忽视,但在潮湿腐蚀环境下的齿轮磨损可靠性预测模型较少,无法进行有效预测。

为解决腐蚀环境下齿轮磨损可靠性预测问题,笔者通过对齿面腐蚀坑的萌生和生长进行概率表征,量化腐蚀坑对赫兹接触的影响及齿面粗糙度随时间的改变,基于Archaed磨损模型,建立考虑腐蚀作用的齿轮磨损故障物理模型,基于可靠性科学原理[13],提出了一种基于性能裕量的齿轮磨损可靠性分析方法,对腐蚀环境作用下的齿轮磨损可靠性进行有效预测。

1 城市轨道齿轮齿面腐蚀表征

潮湿空气中富含的极性阴离子和二氧化硫等可溶于水的高氧化性物质,通过“呼吸”作用进入齿轮箱内部发生冷凝后,会造成金属表面发生氧化甚至腐蚀,形成腐蚀坑并改变齿轮表面形貌,促进齿面磨损。

1.1 腐蚀坑的萌生与生长

腐蚀现象的描述需要两个数学模型分别表征腐蚀坑数目的萌生规律和腐蚀坑深度的生长规律。由于钝化现象,腐蚀凹坑的萌生速率随着时间增加而降低[9],不符合齐次泊松过程,可采用强度为λ(t)>0的非齐次泊松过程进行描述,t时间内腐蚀坑数目的期望值为：

(1)

式中：γ、δ分别为腐蚀坑生长过程的形状参数、比例参数。

高盐雾环境下腐蚀坑的生长速率逐渐降低,随着腐蚀时间的增加,峰值的增长趋势也减缓,并且不断产生新的腐蚀坑,形成另一个分布峰值[9]。因此腐蚀坑的最大深度分布呈现“一个主峰和多个小峰”的趋势,可采用对数高斯分布描述。

一个生长周期内,腐蚀坑生长深度的期望表示如式(2)：

(2)

式中：m′为深度均值;v为深度的标准差。

由于钝化现象存在,假设腐蚀坑自萌生后,生长tm小时,达到最大深度hm成为成熟坑。在各个时刻,成熟坑与生长坑并存,因此,T时刻齿面凹坑的数目如式(3)：

μN(T)=μNntm+μN(T-ntm)

(3)

式中：n=⎣T/tm」为T时刻腐蚀坑成熟的周期数;μNntm为T时刻成熟坑期望数目;μN(T-ntm)为生长坑的期望数目。

将腐蚀坑的萌生现象,描述为单位时间内材料的单位面积上生长的腐蚀坑数目,腐蚀坑生长描述为腐蚀坑最大深度随时间的变化,均与材料属性相关。齿轮磨损过程中,为分析腐蚀现象对齿轮磨损造成的不确定性影响,考虑到齿面腐蚀坑的数目由于统计和分析造成的不确定性,以及腐蚀坑在生长过程中,最大腐蚀深度也存在随机性,将描述腐蚀坑数目的形状参数γ、比例参数δ和腐蚀坑最大腐蚀深度hm分别设为服从N(300,90)、N(0.2,0.06)、N(6.5,1.95)的正态分布。则T时刻齿面凹坑数如图1。

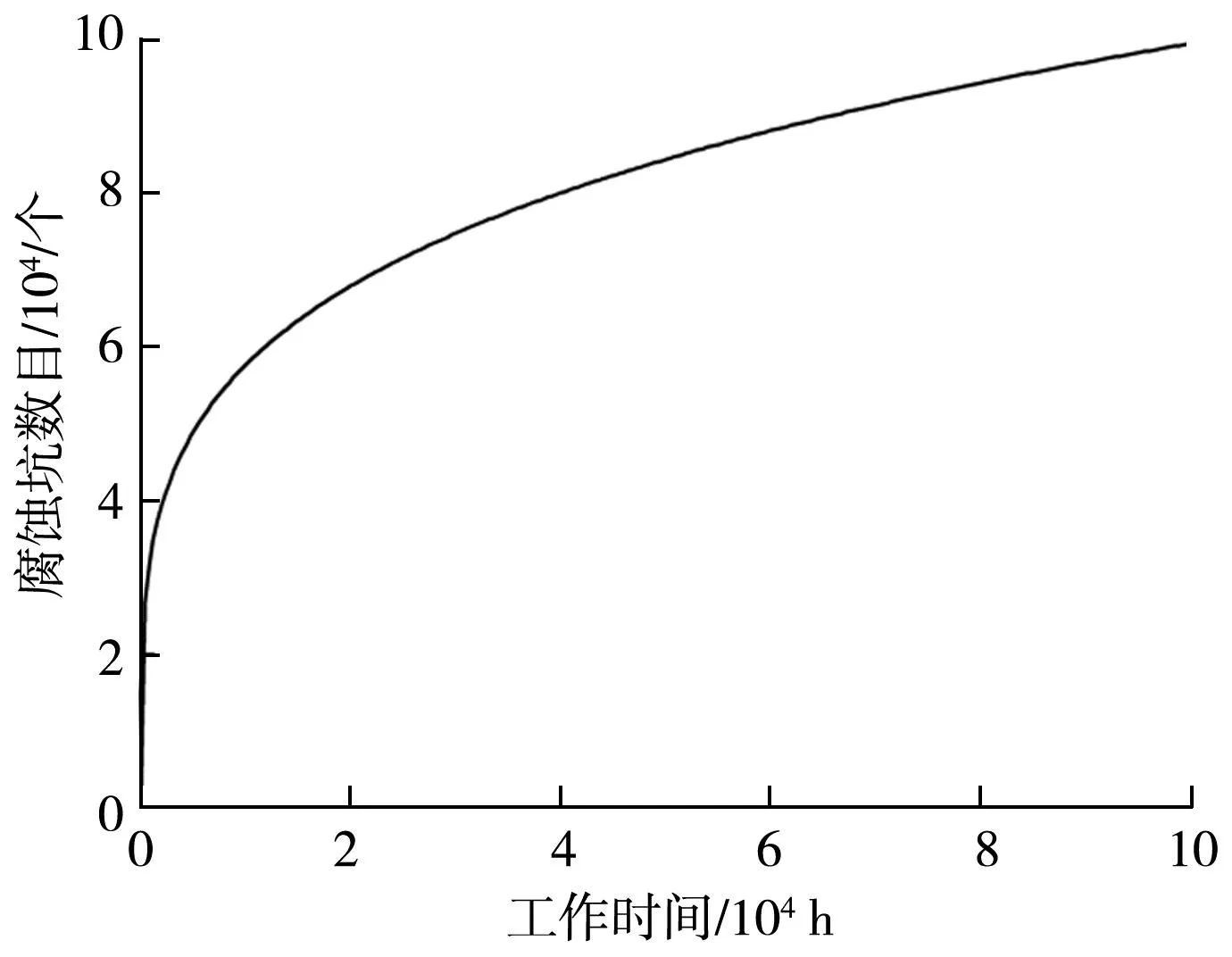
图1 腐蚀坑数目Fig.1 Number of corrosion pits

腐蚀坑的形状可以描述为长椭球体形状,其体积与深度呈正相关,如式(4)：

(4)

式中：h为腐蚀坑深度即椭球体短轴,m1为椭球短轴与长轴比值。

T时刻时,腐蚀坑总体积为成熟坑体积Vm和生长坑体积Vg之和,分别表示如式(5)、式(6)：

(5)

(6)

由于磨损对腐蚀的影响以及表面钝化现象的存在,腐蚀坑的深度和数目会因齿面磨损发生变化。由于钝化作用,腐蚀坑在达到最大深度时停止生长,随着磨损进行,腐蚀坑深度逐渐减小,直至腐蚀坑消失。同时,随着腐蚀的进行,表面钝化现象增强,腐蚀坑萌生速率急剧下降。

因此,假设当齿面磨损深度每次达到腐蚀坑最大深度时,初期萌生的腐蚀坑均由于磨损作用消失,后萌生的腐蚀坑数目较小,可忽略不计,此时表面由腐蚀形成的钝化膜因磨损作用消失,齿面继续腐蚀。

2 齿轮磨损可靠性建模

高接触应力下的齿轮,通常采用混合弹流润滑,基于Archard磨损理论,分析混合弹流润滑下直齿轮的磨损规律。

根据文献[14]齿轮磨损模型,得到沿接触线方向齿轮单次磨损深度分布如图2。可以看出小齿轮齿根处单次磨损深度最大,且小齿轮轮齿啮合次数多于大齿轮,总磨损深度大于大齿轮。

图2 齿轮单次磨损深度 [14]Fig.2 Single wear depth of gear[14]

2.1 齿面磨损分析

在干摩擦情况下,Archard磨损公式表示为：

(7)

式中：V′为磨损量;s为相对滑动距离;Wa是作用在齿面上的接触压力;H为表面硬度;K为无量纲磨损系数。

将渐开线圆柱直齿轮的接触等效为具有时变半径的圆柱滚子接触,圆柱滚子的半径为接触点到基圆上切点的距离如式(8)：

(8)

式中：d0i为齿轮分度圆直径,i=1,2分别表示小齿轮和大齿轮;α0为压力角;y为啮合点到节点的距离。

齿轮的啮合过程分为单齿啮合和双齿啮合,由图2可知小齿轮刚进入啮合时磨损量最大,此时为双齿啮合,双齿啮合过程中,载荷由两对啮合齿轮分配,具体表达式可见文献[14]。

赫兹接触理论指出,法向载荷的作用使得两齿轮接触面会产生局部弹性变形,从而形成一个近似矩形的接触区域,接触应力大小呈椭圆分布,且最大应力出现在接触区域中心位置。考虑腐蚀坑会对齿面微观形貌的改变,会导致接触区域发生缺陷,因此需要对赫兹接触压力进行修正。假设腐蚀坑在齿面上的分布呈现均匀的矩形分布,则有缺陷的赫兹接触区域及应力分布状态如图3。

将被腐蚀坑阻断的接触区域考虑为单个赫兹接触区域,则每个区域的实际载荷表示为：

(9)

式中：F′为无腐蚀坑时的载荷;B为齿宽,N为接触线上腐蚀坑数目;D为腐蚀坑短轴长度。

基于赫兹接触理论,考虑腐蚀坑的齿面赫兹接触半宽αH和赫兹接触压力pp如式(10)、式(11)：

(10)

(11)

式中：F为无腐蚀坑时齿轮总载荷分布;Eeq为等效弹性模量,Req为等效曲率半径,两者具体表达式见文献[15]。

为考虑混合弹流润滑情况下的齿面磨损情况[16],引入粗糙度接触比La和分数膜缺陷系数Ψ。将最大磨损深度处的接触压力、滑动距离带入齿轮磨损,计算得到小齿轮最大磨损深度处单次磨损量hp为：

(12)

式中：V1、V2为小、大齿轮滑动速度;R1为小齿轮曲率半径;E为弹性模量。

2.2 可靠性建模分析

基于可靠性科学的裕量可靠原理[13],采用裕量方程来描述系统的可靠程度。性能裕量(performance margin)表示系统性能参数p与失效阈值pth间的距离,在可靠性计算方面有重要作用。根据系统的失效机理,可得到系统失效的故障物理模型,性能裕量模型可将量化表征的不确定因素纳入分析,从而获得不确定性因素的传播。

对于齿轮磨损而言,可将性能参数p定义为齿轮啮合周期中的磨损深度最大点处的磨损量;当齿轮磨损深度最大点处的磨损量达到最大磨损深度值pth时,判定为齿轮无法满足要求而失效,此时齿面最大磨损深度为单侧齿厚5%[3]。

由于考虑了腐蚀与磨损的交互作用,除了考虑齿轮磨损量,还应考虑腐蚀量以及腐蚀对磨损的促进量造成的齿面材料去除,从而得到考虑腐蚀和磨交互作用下的齿面材料去除的最大深度hDp(t)：

hDp(t)=hCp(t)+hDWp(t)

(13)

式中：hDWp(t)=hWp(t)+hCWp(t)为齿轮最大磨损深度处总磨损量;hCp(t)为腐蚀造成的材料去除量,基于第1节描述,该项可忽略不计;hWp(t)为不考虑由腐蚀作用导致的齿面粗糙度改变下的齿面磨损量;hCWp(t)为由腐蚀作用导致的粗糙度改变下的磨损增量。

将工作时间进行离散,齿轮磨损的退化过程可以描述为T小时后,啮入点处累计的磨损量。只考虑齿轮磨损的磨损深度hWp(t),如式(14)：

(14)

式中：n1为小齿轮转速。

考虑齿轮由于腐蚀作用,齿面粗糙度随时间发生变化,粗糙度定义为：

(15)

式中：l为样条曲线长度;ΔZ为各点到基准面的高度变化绝对值的平均算术偏差。

将粗糙度的定义拓展至三维平面,则由腐蚀坑引起的粗糙度变化,可转化为基准平面内,由腐蚀坑引起的高度变化绝对值的算数平均偏差：

(16)

由腐蚀坑引起的齿面粗糙度随时间的变化采用Sa(t)进行表示：

(17)

式中：B为齿轮齿宽;L为齿轮接触线长度。

(18)

将式(18)带入式(14)得h′p(t),可得考虑腐蚀作用下的齿轮总磨损深度：

(19)

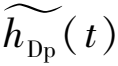
(20)

通过量化磨损量与失效阈值之间的距离,计算性能裕量大于0的概率,基于性能裕量的齿轮磨损可靠度如式(21)：

(21)

R(0)表示t=0时,初始的性能裕量要求,在齿轮啮合过程中,考虑由于齿面腐蚀造成的不确定性,可靠度R(t)难以给出显式计算公式,采用蒙特卡洛抽样算法,得到可靠性演化规律,计算流程如图4。

图4 磨损可靠性计算流程Fig.4 Flow chart of wear reliability calculation

3 齿轮磨损可靠性分析

基于2.1节,将涉及齿轮磨损计算的参数分为确定性参数和不确定参数。表1为某城市轨道交通车辆动力转向架直齿轮副的确定性参数。

表1 齿轮副确定性参数Table1 Deterministic parameters of a gear pair

3.1 考虑腐蚀作用下齿轮磨损可靠性分析

考虑腐蚀作用的齿轮磨损过程中,磨损深度和磨损裕量大小如图5。从图5(a)可见磨损深度随着齿轮啮合次数增加而增加,由于不确定性的存在,磨损量10%～90%之间的宽度随着啮合次数增加而增加,与图5(b)中齿轮磨损的性能裕量的10%～90%之间的规律相对应,齿轮磨损量及其裕量服从正态分布,且不确定性随着操作周期的增加而增加。

图5 齿轮的磨损深度和磨损裕量变化规律Fig.5 Variation rule of wear depth and wear margin of gear

考虑与未考虑腐蚀作用下的齿轮磨损可靠性曲线如图6,同一时刻考虑腐蚀作用的齿面磨损可靠度低于未考虑齿面磨损时,腐蚀作用会促进齿面磨损,且两条曲线随时间增加逐渐逼近,即促进作用随工作时间增加而降低。

图6 齿轮磨损可靠性曲线Fig.6 Gear wear reliability curve

这是由于在腐蚀初期,腐蚀坑的萌生速率和生长速率较大,由腐蚀引起的齿面粗糙度明显增大,因此磨损速率增快,齿轮磨损的可靠度下降更快。随着磨损进程的进行,腐蚀坑萌生速率降低,齿面粗糙度趋于稳定,且由于转矩、最大腐蚀深度等其余不确定性因素的影响,由腐蚀造成的粗糙度变化对齿轮磨损可靠性的影响程度降低。

3.2 灵敏度分析

由于测量和统计误差的不可避免,腐蚀坑萌生服从的非齐次泊松过程的形状参数γ、比例参数δ也不确定。以1.1节中形状参数γ、比例参数δ和腐蚀坑最大腐蚀深度hm服从的正态分布均值和标准差为基准,将正态分布的均值和标准差分别考虑为0.8μ和1.2μ以及0.8σ和1.2σ共4种情况,进行不确定性对可靠度影响的规律分析,如图7。

图7(a)为腐蚀坑生长服从的非齐次泊松过程的形状参数γ变化的可靠性曲线,γ的标准差的变化对可靠性曲线的影响明显弱于均值变化,在相同啮合次数下,γ均值增大,齿轮磨损的可靠性降低。

图7(b)为腐蚀坑生长服从的非齐次泊松过程的比例参数δ变化的可靠性曲线。与形状参数的变化规律相同,δ的标准差变化对可靠性曲线的影响弱于均值变化,且在相同的啮合次数下,随着δ均值增大,齿轮磨损的可靠性越低。

由图7(c)可见,在相同的啮合次数下,随着hm均值增大,齿轮磨损的可靠性越低。随着啮合的进行,当可靠度低于0.3时,标准差越大,可靠性反而更高。当可靠度大于0.9时,hm的标准差变化对可靠性曲线的影响与均值变化接近。随着齿轮啮合过程的进行,标准差对可靠性的影响程度剧下降。

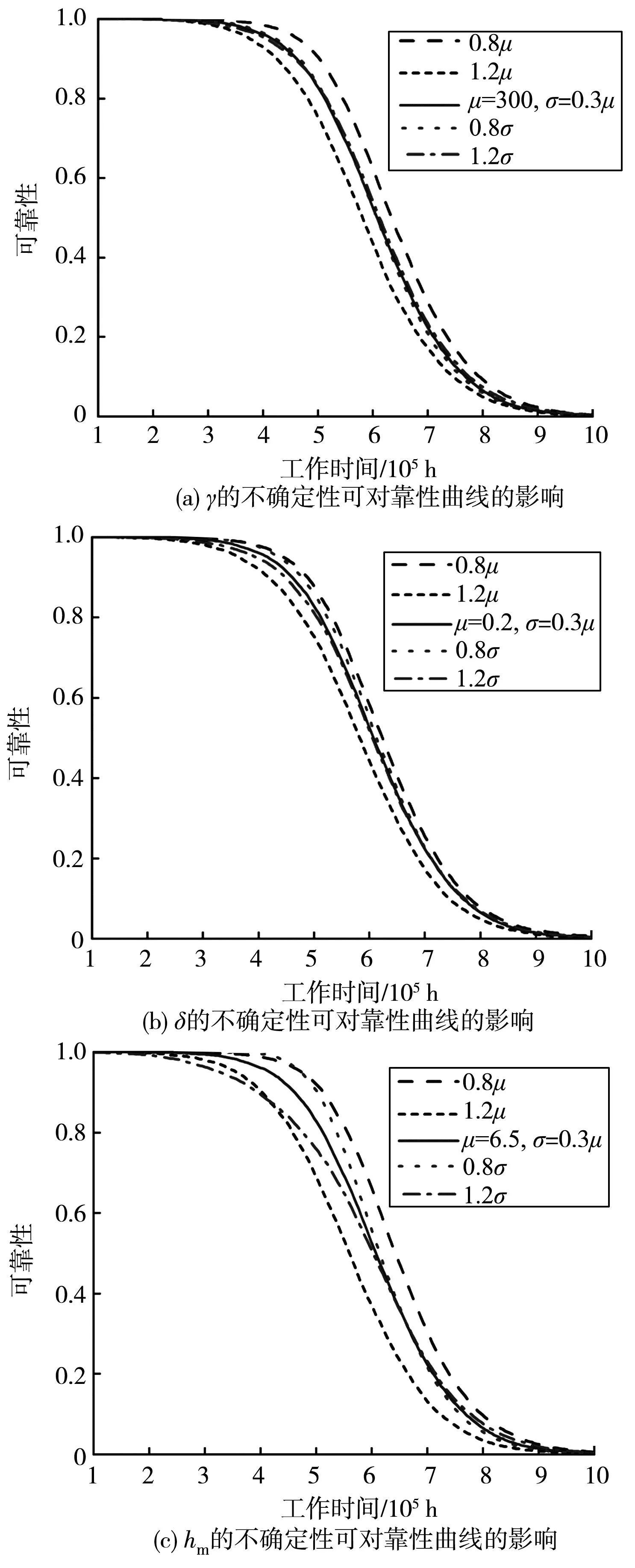
图7 参数不确定性对可靠性曲线的影响Fig.7 Influence of parameter uncertainty on reliability curve

图8为腐蚀坑萌生生长的形状参数γ、比例参数δ和腐蚀坑最大腐蚀深度hm的均值与标准差变化造成的可靠度随时间变化的差值,除γσ外均呈现先增加后减小的趋势,在6×105h左右达到峰值,各参数灵敏度依次为hmμ>γμ>δμ>hmσ>δσ>γσ。

图8 参数不确定性下可靠度差值变化趋势Fig.8 Variation trend of reliability difference under parameter uncertainty

4 结 论

通过分析城市轨道车辆齿轮磨损深度分布规律及腐蚀环境下齿面微小腐蚀坑的萌生和生长过程,推导腐蚀坑体积变化下的齿面粗糙度和赫兹接触应力,以齿轮最大磨损深度最为性能参数,基于性能可靠原理,建立一种腐蚀作用下城市轨道车辆齿轮磨损可靠性预测模型,并对腐蚀坑萌生的形状参数、比例参数和腐蚀坑最大深度对可靠性的影响进行分析,得出如下结论：

1)齿轮磨损量及其裕量服从正态分布。随着工作时间的增长,齿轮累积磨损量的不确定性增加,腐蚀对齿轮磨损可靠性的影响程度降低。

2)工作时间相同时,形状参数γ、比例参数δ和最大腐蚀深度hm均与齿轮磨损可靠性呈负相关关系。

3)腐蚀坑生长过程的比例参数、形状参数和最大腐蚀深度对可靠性的灵敏度依次增加,随着磨损的进行,最大磨损深度hm的标准差对可靠性的影响程度急剧下降。