基于LESO的MMC-RPC反馈线性化直接功率控制

宋平岗,陈 怡,连加巍

(华东交通大学电气与自动化工程学院,江西 南昌 330013)

1 引言

随着国家“碳达峰,碳中和”愿景的提出,铁路运输作为能耗少、污染小的绿色交通运输方式发挥着重要作用.我国电气化铁路牵引供电系统采用单相工频27.5 kV交流供电方式,三相220/110 kV公共电网经过牵引变压器变压后连接至接触网,其中,单相工频电力机车复杂的运行工况及其非线性、不对称性、波动性等特点,必然会使牵引供电系统中的负序电流、谐波、无功及电压波动等电能质量问题日益严峻,进而会影响三相公共电网的供电质量[1].因此,对铁路牵引供电系统电能质量问题进行治理尤为重要.

1993年日本学者提出了应用铁路功率调节器(railway-static power conditioner,RPC)对牵引网的电能质量问题进行治理[2].相比于其他治理方案,铁路功率调节器因其通用性好、系统灵活可控、补偿效果突出等优点,对牵引供电系统中电能质量问题的综合治理效果极佳,目前已成为国内外研究热点,其中,模块化多电平铁路功率调节器(modular multilevel converter-RPC,MMC-RPC)具有模块化程度高、开关损耗小、以直挂式形式接入牵引网、无需外设降压变压器、系统体积小等优势[3],在保留传统RPC性能的同时,有效提高了RPC的容量及系统的性能.

模块化多电平铁路功率调节器作为一种结构复杂的多变量非线性系统,其双闭环比例积分控制[4]稳态误差大,且在将功率外环转换为电流内环参考指令的过程中,受电压采样和锁相环精度的影响大.文献[5]通过合成矢量的方法提出了一种直接功率控制策略,实现了功率的局部解耦控制,但系统稳定性弱,受干扰时跟踪能力差,控制精度低.在RPC的扰动处理问题上,为了降低参数摄动等扰动对系统性能的影响,文献[6]设计了一种基于µ综合控制的鲁棒控制器,但是该控制器的设计需要预先知道扰动项,并且参数变量多,求解复杂.文献[7]利用微分平坦理论,设计了MMC-RPC的双环控制策略,使得MMC-RPC的输出值跟踪参考指令值,但是系统的前馈控制量受误差反馈的影响大,对扰动的估计和补偿效果欠佳.

反馈线性化控制是一种基于微分几何理论的非线性控制方法,通过将非线性耦合系统转化为独立的线性子系统,实现精确解耦[8],目前已应用于船舶变频器[9]、永磁同步电机[10]、电力系统[11]等领域.在RPC系统中,文献[12]设计了一种反馈线性化双闭环控制策略,但是该控制策略需要复杂的坐标变换,并且由于反馈线性化控制理论来源于标称模型,其对系统参数摄动等不确定因素的干扰敏感,系统鲁棒性难以保证.于是,有学者提出与观测器结合来保证系统的动态响应性能[13].

线性扩张状态观测器(linear extended state observer,LESO)来源于线性自抗扰控制[14],其思想是通过将扰动项扩张成新的状态变量,然后用相应的反馈机制将扰动项观测出来.线性扩张状态观测器设计简单不需要具体的数学模型,在无人机[15]、光电跟踪系统[16]等领域广泛应用.

然而,在MMC-RPC领域中,却鲜有文献将反馈线性化和线性扩张状态观测器结合来提升系统的控制性能.基于以上研究背景,文章以MMC-RPC为研究对象,针对文献[5]所提传统直接功率控制不能实现功率完全解耦、受不确定因素影响大且控制精度低的问题,提出了一种基于线性扩张状态观测器的反馈线性化直接功率控制方法.线性扩张状态观测器不需要被控对象精确的数学模型,设计简单,观测能力强;采用状态反馈线性化控制实现对功率的精确解耦控制,提高系统的动态响应能力,无需锁相环和复杂的坐标变换,简化了控制器的设计.最后,在MATLAB/Simulink中搭建了仿真模型进行验证.

2 MMC-RPC拓扑结构和补偿原理

2.1 MMC-RPC拓扑结构

模块化多电平铁路功率调节器由两个单相H 桥结构的模块化多电平换流器(single-phase H-bridge MMC,SPH-MMC)背靠背连接而成,三相公共电网(220/110 kV)经V/v 牵引变压器降压后,将27.5 kV单相工频电压传输给铁路牵引供电网,两个SPH-MMC分别挂接于牵引网馈线两侧.其结构如图1所示.

图1 MMC-RPC牵引供电系统简化结构图Fig.1 Simplified structure diagram of MMC-RPC traction power supply system

图1中:iA,iB,iC为牵引变压器原边三相电压;iL,iR为流经牵引供电网左右两侧供电臂电流;iLa,iLb,iRa,iRb为流入SPH-MMC的电流;R0,L0为线路等效电阻和电感.

由于两侧SPH-MMC结构完全对称,因此,选取其中一侧进行分析.将其中一侧SPH-MMC单独取出,如图2所示.

图2 单侧SPH-MMC的拓扑结构图Fig.2 Topological structure diagram of single-sided SPHMMC

图2中:Ls,Rs为上下MMC桥臂的等效电感和电阻;eab(eab=ea-eb)为交流侧端口电压;uap,uan分别为上下MMC桥臂电压之和;iap,ian为流经上下桥臂的电流;idc,udc为直流侧输出电流和电压;右下侧框图为MMC子模块SM的内部结构图.

以a相上下MMC桥臂为例,根据KVL定律得到SPH-MMC交流侧和直流侧电压方程为

将式(1)中交流侧端口电压方程和直流侧电压方程经过相加、相减运算可以得到交流端口和直流端口数学方程,如式(2)所示.

通过式(2)可以清晰的看出,通过控制MMC上下桥臂中子模块的投切数量可以实现对交流侧和直流侧电压的控制,进而实现对牵引供电系统的电能质量的综合治理.

2.2 MMC-RPC功率补偿指令分析

在对牵引供电系统电能质量治理中,通过平衡有功补偿无功的方式消除负序电流.

定义牵引网两侧供电臂为L侧和R侧,假设R侧重载,L侧轻载.图3为V/v牵引变压器补偿前后电压、功率向量图.

图3 RPC功率补偿前后分析图Fig.3 Analysis before and after RPC power compensation

图3中:PL,QL和PR,QR为两侧供电臂的有功和无功功率;=+,=+为补偿后两侧供电臂上的功率;pRref,qRref为MMC-RPC 在电能质量治理过程中R 侧向供电臂提供的补偿功率;pLref,qLref为L侧向供电臂提供的补偿功率.由图3可知,各功率量之间满足以下表达式:

其中:和的表达式如式(4)所示,30◦为理想状态下的功率因数角.

3 功率数学模型

由于铁路采用单相供电方式,只有一个单一的自由度无法直接进行dq坐标变换,因此,文章采用SOGI[5]构造虚拟正交分量,则SPH-MMC交流侧数学方程式(1)在αβ坐标系下可表示为

而网侧电压在αβ坐标系分量usα,usβ还可表示为[17]

其中:Um为网侧电压的幅值,ω为系统频率.

单相系统在αβ坐标系下的瞬时有功/无功功率表达式为

对功率进一步求导可得

将式(6)–(7)带入式(8)后经过化简可得

其中fp,fq的表达式为

从式(10)可知,其功率模型是一个强耦合的非线性系统.经典的PI控制难以实现交叉耦合的精确解耦[18],不能对系统内部变化做出良好的响应,因此需采用有效的解耦方法对系统进行解耦控制.文章采用状态反馈精确线性化方式对系统进行解耦.

4 非线性系统反馈线性化

对于非线性系统进行反馈线性化可解的前提条件是系统存在相对阶ρ1,ρ2,···,ρm,且满足ρ1+ρ2+···+ρm=n,其中n为系统状态变量的维数[18].根据相对阶原理,利用Lie导数,将非线性系统转化为标准型,从而可以利用反馈线性化来设计控制器,使得非线性系统跟踪目标.

4.1 Lie导数

对于一个单输入–单输出系统

对系统的输出y关于时间t进行求导可得

式中Lfh(x),Lgh(x)分别为输出h(x)沿着f(x),g(x)的Lie导数.

4.2 反馈线性化控制器设计

在功率耦合公式(10)中,定义X=[x1x2]T=[p q]T,u=[fpfq]T,Y=h(X)T=[p q]T,则耦合项的紧缩形式可以表述为两输入、两输出的仿射非线性模型

因此,对照式(12),经过计算可以得到功率耦合项的解耦矩阵表达式为

由式(14)可知,系统的相对阶满足:ρ1=ρ2=1,ρ1+ρ2=2.则系统满足精确化线性解耦条件,可以对其进行线性化解耦.

令v为系统新的输入变量,则存在矩阵A(x),E(x),使得输入变量v满足

式中:A(x)的表达式如式(14)所示,E(x)为

则新的输入变量表达式变为

则系统变为一阶典型系统,可以按照一阶系统设计控制器

则解耦控制器表达式为

其中v1,v2采用比例积分调节器

此外,由于MMC-RPC为两个单相H桥结构的MMC背靠背连接而成,要求系统能够很好的稳定直流侧输出电压,保障系统可靠运行.因此,有功功率参考值的获取参考文献[5],表达式如下:

在对系统进行精确反馈线性化控制时,模型未建模参数或者其他参数摄动等不确定因素干扰下会影响控制器的性能[19].因此,需要相应的控制器进行扰动的观测与补偿,下面将采用线性扩张状态观测器对扰动进行观测和补偿.

5 线性扩张状态观测器

5.1 LESO原理

假设存在未建模参数或者其他参数摄动等不确定因素影响系统输出特性.对于一阶系统˙y=f(x)+bu可以如下表示:

式中:ε为影响系统输出的干扰项,b为控制器增益.而线性扩张状态观测器的建立并不需要具体的模型,只需知道被控对象的控制量和输出量,因此,为简化控制器的设计,将f(x,ε)统称为ξ,则式(22)可以改写为如下形式:

选取新的状态变量,令x1=y,x2=ξ,则式(23)扩张为一个新的状态变量

采用龙贝格观测器设计线性扩张状态观测器如下:

式中:z1,z2为x1,x2的观测值,β1,β2为观测器增益.至此,可以通过线性扩张状态观测器将扰动项观测出来,使得反馈线性化控制更为精确.

5.2 直接功率线性扩张状态观测器设计

以有功功率为例,即

令x1=p,x2=ξ,则将式(27)扩张成一个新的状态方程

则扩张状态观测器设计如下,写成状态方程形式:

参数β1,β2按照极点配置的方法设计.

则可以得到β1=2ω0,β2=,其中ω0为观测器带宽.

同理,设计无功功率分量的线性扩张状态观测器.

最终得到控制率的设计为

针对MMC-RPC的反馈线性化模型,设计形式简单的线性扩张状态观测器来求解模型有功功率p和无功功率q的观测值,即可消除由于扰动量引起的对精确反馈线性化控制性能的影响.

注1因β轴分量不具有实际的物理意义,将其舍去.则根据式(9)可以得到被控对象模型表达式如下:

由于MMC-RPC上下桥臂交流侧电压大小相等,方向相反,则两相桥臂交流电压期ea=-eb=eα/2,进而实现对SPH-MMC的调制.

综上所述,基于LESO的MMC-RPC反馈线性化直接功率控制框图如图4所示.

图4 MMC-RPC控制框图Fig.4 MMC-RPC control block diagram

注2由于MMC-RPC 左右两侧对称,图4 仅给出了MMC-RPC左侧的控制框图.

6 仿真分析

为了验证本文所提基于LESO的MMC-RPC反馈线性化直接功率控制方法在电能质量治理的优越性和有效性,在MTALAB/Simulink 中搭建了本文所提控制方法和传统直接功率控制方法下的MMC-RPC仿真模型,模拟V/v牵引变压器处于最大不平衡状态下的功率补偿效果,即仅存在一侧供电臂有电力机车负载运行.具体仿真电路参数如表1所示.

表1 MMC-RPC仿真参数Table 1 MMC-RPC simulation sarameters

6.1 电流波形分析

设仿真模型中右侧供电臂机车负载有功功率为16 MW,无功功率为4 MVar.左侧供电臂机车处于空载状态.在t=0.2 s时,MMC-RPC 投入运行,开启电能质量治理,并和传统直接功率控制方法进行对比,仿真结果如图5–6所示.

图5 两种控制方法下补偿前后电流波形图Fig.5 The current waveforms before and after compensation under the two control methods

图6为图5两种控制方法下,MMC-RPC投入瞬间V/v牵引变压器原边电流放大后的对比波形图.从图中可知,当MMC-RPC投入运行后,本文所提控制方法能够平稳、迅速响应,使得V/v牵引变压器原边电流迅速恢复平衡,实现电能质量治理的效果.而传统直接功率控制方法下V/v牵引变压器原边电流在RPC投入运行的过程中发生畸变,经过短时的波动后才恢复至三相平衡状态.仿真结果验证了本文所提基于线性扩张状态观测器的反馈线性化直接功率控制方法在MMC-RPC电能质量治理上的优越性.

图6 电流波形放大对比图Fig.6 Current waveform method comparison chart

6.2 功率波形分析

1)MMC-RPC左侧功率波形对比分析.

保持第6.1节的仿真工况,由于MMC-RPC两侧对称,选择左侧功率进行分析,并和传统直接功率控制方法中的功率波形进行对比.结果如图7所示.

图7 MMC-RPC左侧功率波形图Fig.7 The left power waveform diagram of MMC-RPC

从图7可以看出,相比于传统直接功率控制,文章所采用的基于LESO的反馈线性化直接功率控制策略下MMC-RPC的输出功率波形波动范围小,能够精确跟随功率指令值,实现了更加精确的补偿效果.

2)LESO功率观测波形分析.

当系统受到系统参数摄动或者其他因数干扰时,系统的传输功率将会受到影响,进而会影响整个系统的性能.利用LESO可以对系统的扰动进行观测和补偿,消除不确定性因素对反馈线性化控制跟踪效果的影响.因此,LESO的观测能力的好坏直接影响到系统的整体性能.同样,由于两侧对称,以右侧供电臂为例,图8为右侧供电臂功率输出值/功率观测值波形图.

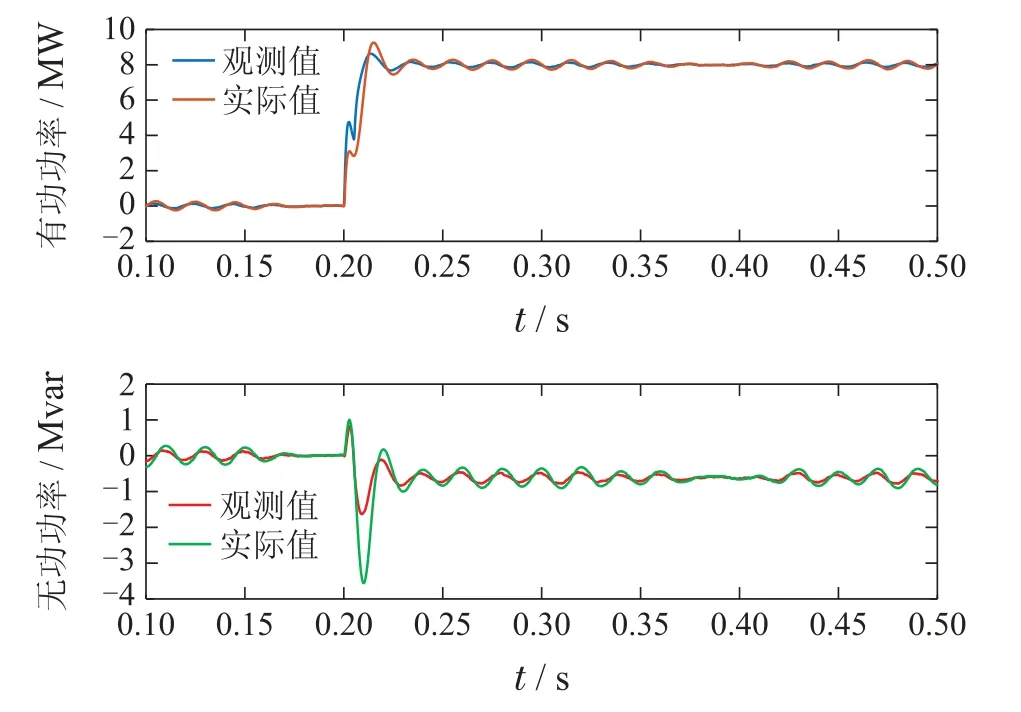
图8 右侧供电臂功率输出值/观测值波形图Fig.8 Waveform diagram of power output value and power observed value

从图8中可以看出,LESO能够对功率输出值实现良好的观测效果,进而可以消除不确定性扰动对功率跟踪能力的影响.

6.3 直流侧电压波形分析

MMC-RPC采用两个单相SPH-MMC背靠背连接,要求系统能够很好控制直流侧输出电压的稳定.图9为两种控制方法下直流侧电压波形对比图.

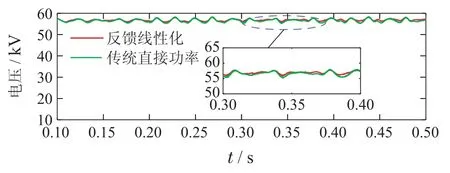
图9 直流侧电压波形图Fig.9 DC side voltage waveform diagram

从图9中可知,传统直接功率控制方法和文章所采用的基于LESO的反馈线性化直接功率控制都能够实现直流侧电压的稳定输出.但经过放大对比可知,文章采用的控制方法直流侧电压波动较小,可以使得生成的功率参考值更加精确.

6.4 两种工况下MMC-RPC仿真分析

为进一步验证基于LESO的反馈线性化直接功率控制在MMC-RPC不同工况下对牵引网的电能质量治理和补偿效果,仿真模拟两种工况,并和传统直接功率控制方法进行对比.

工况1 模拟机车负载突变时MMC-RPC治理效果.假定文章所采用控制方法下的MMC-RPC已经投入运行,最大不平衡状态下只有一侧供电臂有负荷.设右侧供电臂在0.2前有功功率为16 MW,无功功率为4 MVar,0.2 s时,负荷增加了有功功率20 MW,无功功率1.2 MVar,0.4 s时负载恢复至0.2 s前的状态.波形图如图10–11所示.

图10 负载突变时电流波形图Fig.10 Current waveform diagram when the load changes suddenly

图10为负载突变时文章所提控制方法下V/v牵引变压器原边电流和左右供电臂电流波形图,从图中可知,在负载突变时,所提控制策略下MMC-RPC能够迅速响应,对原边电流和两侧供电臂电流进行补偿,动态性能好.体现了所采用的基于LESO的反馈线性化控制方法对铁路牵引供电系统电能质量优越的治理能力.

图11为文章所提控制方法和传统直接功率控制方法下,负载突变时MMC-RPC右侧供电臂功率波形对比图.图11(b)–(c)为图11(a)椭圆框图放大后的对比图.从图中可知,文章所提控制方法下,有功、无功功率波动小,能够精确跟踪参考指令值.而传统直接功率控制方法,有功功率波动大,无功功率不能精确跟踪参考指令值.对比结果验证了文章所提控制方法的优越性.

图11 负载突变时功率对比波形图Fig.11 Comparison waveform of load sudden change power

工况2 模拟机车负载过分相,即潮流发生反转时的治理效果.假定文章所采用控制方法下的MMCRPC已经投入运行.设0.2 s前右侧供电区间所带机车有功、无功负荷为(16+j4)MVA,左侧供电区间无机车负载运行.0.2 s时机车进入分段换相区(供电死区),0.3 s时机车负载由右侧供电臂进入左侧供电臂区间运行,完成过分相.仿真结果如图12–13所示.

图12 负载过分相时电流波形图Fig.12 Current waveform when the load is excessive

图12为负载过分相,发生潮流反转时,文章所提控制方法下V/v牵引变压器原边电流和左右供电臂电流波形图.从图中可知,本文所提控制方法下的MMCRPC能够在快速应对负载过分相,补偿V/v牵引变压器使得电流快速恢复平衡.并且从图13的功率波形图可知,当潮流发生反转时,通过平衡两侧供电臂的有功功率,补偿无功功率来消除负序电流,实现三相平衡,达到了电能质量治理的效果.

图13 负载换相时功率对比波形图Fig.13 Comparison waveform of load commutation power

图13为文章所提控制方法和传统直接功率控制方法下,负载过分相时MMC-RPC右侧供电臂功率波形对比图.图13(b)–(c)为图13(a)椭圆框图放大后的对比图.从图中可知,文章所提控制方法下,有功、无功功率波动小,能够精确跟踪参考指令值.而传统直接功率控制方法,有功、无功功率波动大,不能精确跟踪参考指令值.对比结果验证了文章所提控制方法的优越性.

7 结论

文章通过分析MMC-RPC的工作原理和数学模型,为解决传统直接功率控制下,受系统内外部不确定性因素干扰,功率跟踪效果差,控制精度低的问题.提出了一种基于LESO的反馈线性化直接功率控制方法.通过LESO消除扰动的影响,利用反馈线性化理论对功率进行精确解耦控制.通过仿真分析得到以下结论:

1)与传统直接功率控制相比较,文章所采用控制方法下,直流侧输出电压更加稳定;功率跟踪效果好,精度高,具有良好的动态响应能力;所采用的LESO观测器能够对功率输出值实现良好的观测效果.

2)所提控制方法下,MMC-RPC能够迅速响应机车负载突变和过分相工况,动态响应速度快,功率波动小,能够快速实现对铁路牵引供电系统电能质量的治理.