制冷站双目标权重自适应非线性预测控制
魏 东闫 畔冯浩东
(1.北京建筑大学电气与信息工程学院,北京 100032;2.北京市建筑大数据智能处理重点实验室,北京 100032;3.北京北方华创微电子装备有限公司,北京 100176)
1 引言
制冷站作为公共建筑中央空调系统的核心,其能耗占整个建筑空调系统能耗的60%左右[1].能效比(energy efficiency ratio,EER)是衡量制冷站能效的标准[2],美国采暖、制冷与空调工程师学会(ASHRAE)指出:EER在4.1以上为高能效制冷站,而国内制冷站EER通常只能达到2.5∼3.2 的平均水平[3].控制方法不当是造成这种现象的主要原因.目前制冷站大多采用(proportional-integral-derivative,PID)控制方法实现独立设备回路的闭环调节,无法满足系统整体性能优化要求.同时,制冷站非线性和大滞后的特性导致PID参数整定困难,系统极易产生震荡.因此,研究自适应性强的制冷站节能优化控制策略意义重大.
研究表明,模型预测控制(model predictioncontrol,MPC)能够通过实时反馈克服干扰等不确定性因素的影响,解决耦合和硬约束问题,拥有较好的动态控制性能[4].Uwe等人[5]提出一种吸附式制冷机预测控制算法,采用序列二次规划法(sequential quadratic programming,SQP)解决滚动优化问题,使制冷机的冷却能力比在状态控制下提高31.1%.Zhao等人[6]提出一种基于动态规划(dynamic programming,DP)的预测控制方法,将情景分析与预测控制相结合,实现了光伏蓄冰空调系统的经济运行.
上述策略虽取得了较好的控制效果,但求解优化问题时采用的非线性规划法(如SQP,DP)计算量较大,占用存储区空间较多[7],为工程实现带来了困难.针对上述问题,Seong和Widrow[8]提出了一种基于神经网络的非线性多输入多输出优化求解算法,采用神经网络计算反馈最优解,降低了时间、空间复杂度.然而,该算法本质上属于最优控制问题,不适用于制冷站这种时变且易受扰动等不确定因素影响的复杂系统.
另一方面,为满足系统整体性能优化要求,制冷站预测控制策略优化目标应为在满足建筑冷量需求的前提下,提高系统整体能效.然而,这两个优化目标之间存在矛盾关系.为解决多目标优化过程中各子目标相互冲突的问题,许志荣等人[9]采用线性加权方法进行双目标问题求解,但该方法的权重系数不能实时修正,不适用于场景与变化较为复杂的工业应用.史晨豪等人[10]基于改进的NSGA-Ⅱ算法求解配电网双目标优化函数,但该算法由于种群收敛分布不均匀,易陷入局部最优,求解结果的优劣程度难以保证.而在能够充分采集系统运行数据的情况下,采用模糊逻辑(fuzzy logic,FL)基于先验知识构建权重自适应模块是一种易于实现的解决方案,因为模糊逻辑作为一种类似于人类推理的决策方式,其特点是无需依赖精确的被控对象模型,仅需基于先验知识进行推理,易于工程实现[11].
综上,本文提出制冷站双目标权重自适应非线性预测控制策略,优化目标分别为满足建筑冷量需求和提高系统整体能效,为解决非线性规划算法计算量大、制冷站时变且易受扰动的问题,对文献[8]所提的方法进行改进,提出基于神经网络的预测控制算法.该算法结合多步预测、在线滚动优化和反馈校正策略,采用3层前馈神经网络作为优化反馈控制器,将系统优化目标函数作为神经网络控制器在线寻优性能指标,基于Euler-Lagrange算法和随机梯度下降法,对神经网络控制器权值进行滚动优化.在此基础上,在控制策略中加入优化目标函数权重自适应模块,采用模糊逻辑分派策略求解权重因子,对预测控制优化目标函数进行动态调整,以平衡优化目标函数中系统制冷量和制冷站能效比之间的矛盾关系.最后以广州某公共建筑制冷站为研究对象进行仿真实验,验证了所提方法的有效性.
2 系统描述
2.1 制冷站系统描述
制冷站由3部分构成,分别为制冷机组、冷冻水回路和冷却水回路.其中: 制冷机组是中央空调的制冷源;冷冻水回路由冷冻水泵及冷冻水管道组成,冷冻水流出制冷机后,通过末端空气处理机组中的冷却盘管与空气进行热交换,带走空气中的热量,再将热量传送给制冷机组中的制冷剂;冷却水回路由冷却水泵、冷却水管道及冷却塔组成,冷却水在制冷机中带走制冷剂释放的热量,再通过冷却塔与大气进行热交换.
2.2 制冷站能效分析
2.2.1 制冷机组
制冷机组是制冷站中的核心设备,其制冷量由式(1)计算得出,即
其中:Qch表示制冷机组制备的冷量(制冷站提供的冷量),单位kW;c表示水的比热容,单位J/(kg·K);mchw表示冷冻水流量,单位kg/s;Tchws表示冷冻水供水温度,单位◦C;Tchwr表示冷冻水回水温度,单位◦C.
制冷机组的运行能效比COP(coefficient of performance)是所制备的冷量与制冷机组运行功率之比
其中:Pchiller表示制冷机组的运行总功率,单位kW;Qch表示制冷机组制备冷量,单位kW.
2.2.2 水泵
在制冷站中,冷冻水泵和冷却水泵是完成冷冻水循环、冷却水循环所必要的动力设备.一般情况下,水泵的功率由变频器控制,计算公式为
其中:Ppump表示水泵功率,单位kW;ρ表示冷冻(却)水密度,单位kg/m3;g为重力加速度,单位m/s2;V表示冷冻(却)水流量,单位m3/h;H表示水泵扬程,单位m;η表示水泵全效率;ηp为水泵效率;ηm为电机效率;ηVFD为变频器效率.
2.2.3 冷却塔
制冷站内的冷却塔利用风机对带有热量的冷却水进行降温散热.冷却塔风机运行功率可表示为
其中:Ptower表示风机运行功率,单位kW;Ptower,rated表示风机额定功率,单位kW;ft表示风机运行频率,单位Hz;f0表示风机额定频率,一般为50 Hz.
2.2.4 制冷站能效比
制冷站能耗指标EER为制冷站在单位时间内的制冷量与其消耗功率的比值,计算公式为
其中:Pchiller为制冷机组运行功率,Ppumpch,Ppumpc分别为冷冻水泵、冷却水泵运行功率,Ptower表示冷却塔风机运行功率,上述变量单位均为kW.
制冷机组能耗占制冷站总能耗的一半以上,Tchwr不变时,提高Tchws可以提升制冷机组COP[12].由于制冷机组内部控制器不允许对其进行直接控制,因此求取制冷站能效比最高时的冷冻水供水温度设定值,并将其传送给制冷机组内部的控制器,可以实现对Tchws的控制.由式(3)–(4)可知,可以通过调节水泵和风机的运行频率改变水泵和风机功率.因此,制冷站EER的控制变量分别为Tchws,fpumpch,fpumpc以及冷却塔风机转速ftower.同时,由式(1)可知,Tchwr不变时,制冷机组制冷量Qch与mchw,Tchws直接相关,而mchw通过改变fpumpch进行控制,因此制冷量Qch的控制变量为fpumpch和Tchws.
3 预测控制策略
3.1 预测控制优化目标函数
控制目标是在满足建筑冷量需求的前提下,尽可能提高制冷站整体能效,使得系统EER跟随其设定值、制冷量跟随需求负荷值.同时,引入权重因子α平衡制冷量与EER的权重关系,实现优化控制.综上,制冷站预测控制优化目标函数定义为
式中:J(EER)[k]表示预测控制优化目标目标函数,M为预测时域,t1为预测时域的起始时间,EER[k]和Qch[k]表示当前时刻系统能效比和制冷量,EERset[k]和Qpred[k]表示当前时刻能效比设定值和负荷设定值(将负荷预测结果作为设定值),α是当前时刻权重因子,其定义域在[0,1]之间.
3.2 预测控制系统结构
制冷站预测控制系统由预测控制模块和权重自适应模块组成,系统结构如图1所示.其中,预测控制模块由负荷预测模型、系统能效比预测模型和神经网络预测反馈控制器组成,通过多步预测、滚动优化和反馈校正策略,对神经网络控制器权值和阈值进行在线寻优,求出最佳的控制量;虚线框所代表的权重自适应模块通过模糊逻辑得到权重因子α,实时更新优化目标函数(6)中两个目标的权重.
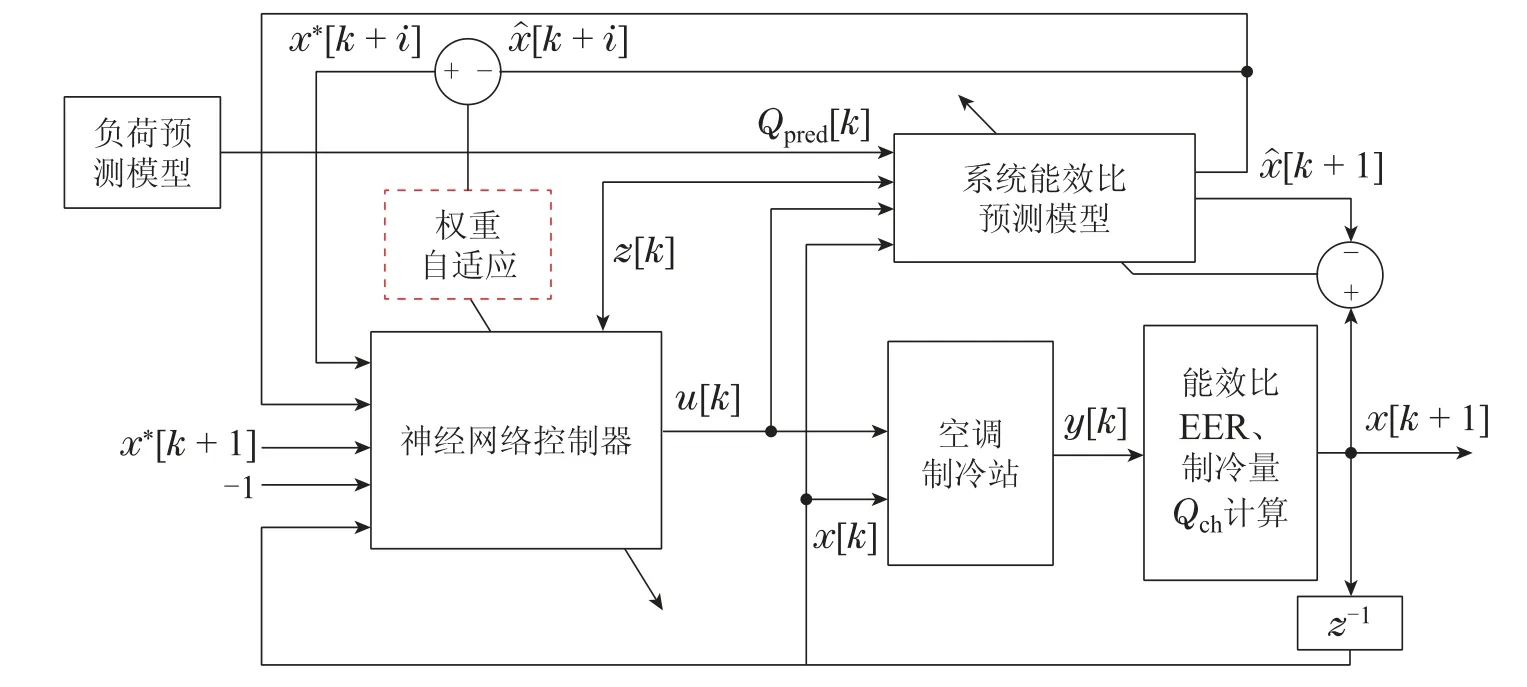
图1 系统预测控制策略结构图Fig.1 System predictive control strategy structure diagram
图1中,状态变量x[k]包含当前时刻EER值EER[k]和当前时刻制冷量Qch[k];ˆx[k+i]为EER 预测值;x∗[k+i]为EER的期望值和负荷的预测值;y[k]为冷冻水流量、冷冻水供回水温度等参数的实际值;z[k]为室外温度、室外湿度等其他变量.
由第2.2.4小节可知,制冷站需要寻优的控制变量u[k]=(Tchws[k],ftower[k],fpumpch[k],fpumpc[k]).
此外,制冷站各设备均受到一定条件的状态约束,控制量参数的取值范围为
冷冻水供水温度:7◦C ≤Tchws≤15◦C;
冷冻水泵控制频率:30 Hz ≤fpumpch≤50 Hz;
冷却水泵控制频率:30 Hz ≤fpumpc≤50 Hz;
冷却塔风机控制频率:30 Hz ≤ftower≤50 Hz.
3.3 权重自适应模块
权重自适应模块采用模糊逻辑对权重因子进行寻优,由EER[k]与其设定值EERset[k]得到能效比差值∆EER,由系统提供冷量Qch[k]与需求负荷Qpred[k]得到冷量差值∆Q,实时调整制冷量与能效比的权重因子α,实现制冷站的节能优化运行.
3.3.1 模糊论域
模糊论域输入变量为E(∆EER)和Q(∆Q).对于所研究的制冷站而言,E的取值范围为[-2.5,1.75],Q的取值范围为[-380,250],两者真实值之间的差值过大,因此通过尺度变换得到输入变量E的论域为[-0.25,0.175],Q的论域为[-0.38,0.25].尺度变换后论域较为精细,因此模糊论域为[-2,-1,0,1,2],模糊子集T=[NB(负大),NS(负小),ZO(零),PS(正小),PB(正大)].
3.3.2 隶属度函数
在输入变量E,Q较为密集的区域(如E的ZO区域)使用较平缓的高斯隶属度函数,而在其他较为分散的区域使用三角隶属度函数.输出变量α的隶属度函数为高斯型.最终确定的E,Q以及α的隶属度曲线如图2所示.
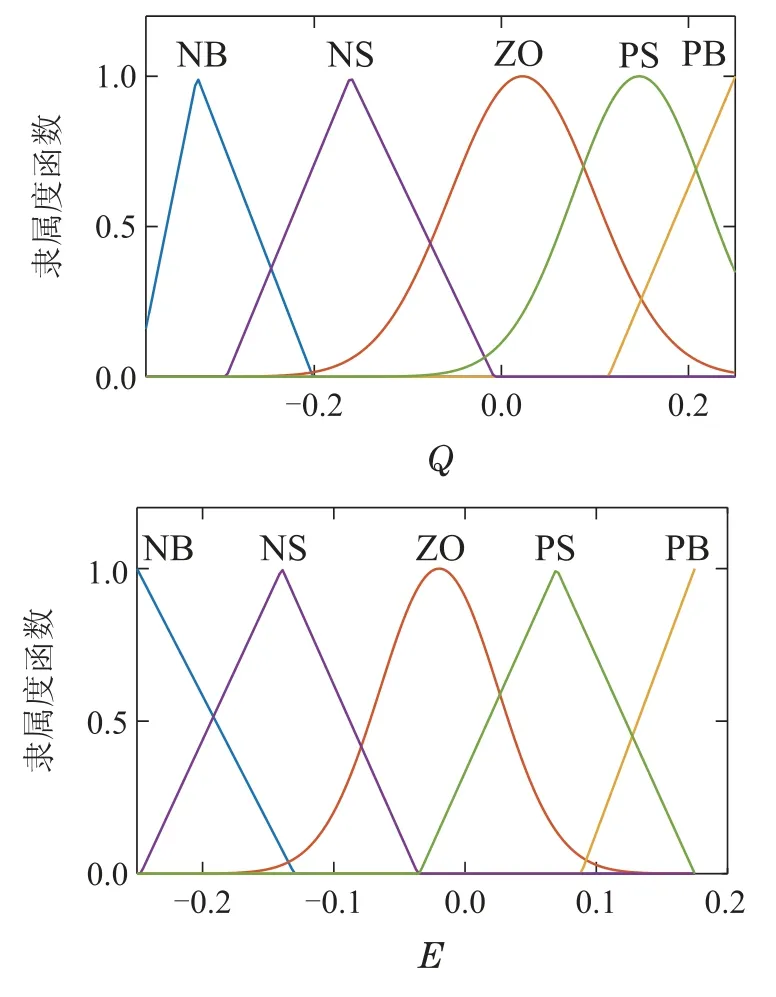

图2 各变量隶属度函数曲线Fig.2 The membership function curve of each variable
3.3.3 模糊规则
模糊规则设置依据如下: 1)∆EER较大,∆Q较小时,控制系统的主要任务是消除能效比偏差,α应偏小;2)∆EER较小,∆Q较大时,控制系统的主要任务是消除冷量偏差,α应偏大.
参照制冷站运行规律和实际控制操作经验,在仿真过程中不断调整被控量精度,得到模糊规则表如表1所示.
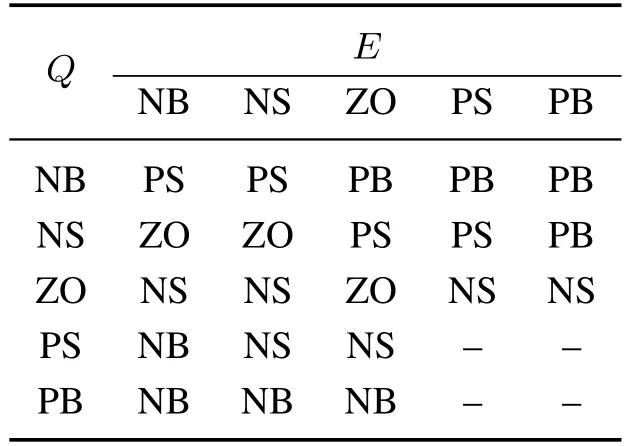
表1 模糊规则表αTable 1 Fuzzy rule table α
3.4 非线性预测控制
3.4.1 神经网络非线性预测控制算法
制冷站由制冷机组、水泵、风机等非线性设备组成,非线性系统预测模型的一般表达式为
其中:x[k]=[x1(k)x2(k)x3(k)··· xn(k)]表示n维状态变量,u[k]=[u1(k)u2(k)u3(k)··· um(k)]表示m维控制变量,k为当前时刻,k+1 为下一时刻.
神经网络控制器的表达方式如下:
其中:W表示神经网络权值矩阵(包括阈值);x∗[k+1]表示下一时刻状态变量的期望输出.神经网络控制器输入层有2n+1个神经元,输入变量为x[k],x∗[k+1]和-1,输出层有m个神经元,输出变量为控制量u[k].
不失一般性,设预测时域内的优化目标函数为
式中:ϕt1+M(x[t1+M],t1+M)表示末值优化目标函数,L(x[k],u[k],k)表示过程优化目标函数.
采用拉格朗日乘子法[13],引入待定的拉格朗日乘子向量,构造增广优化目标函数
其中:λ和q分别为n维和m维拉格朗日乘子向量,f(k)和g(k,W)分别代表预测模型(7)和控制器方程(8)的右侧部分,则可得到哈密顿函数
于是增广优化目标函数可以改写为
假设状态变量、控制量和神经网络控制器权值矩阵(包括阈值)的变分分别为δx[k],δu[k]和δW,为了求取增广优化目标函数的极值,求取式(12)的一阶变分
对于任意变分向量δx[k],δu[k]和δW,最小化增广优化目标函数Ja的必要条件是δJa=0.由于x[t0]是已知常量,故δx[t0]=0.
则需满足以下条件,使增广优化目标函数极小:
其中: 式(14)–(15)为哈密顿正则(伴随)方程,k=t1,t1+1,···,t1+M -1;式(16)为横截条件;式(17)为极值条件.
3.4.2 制冷站神经网络预测控制器设计
在神经网络控制器中,增加隐含层的数目可以提高网络的非线性映射能力,但同时会影响网络的泛化能力.理论研究表明,3层神经网络能以高精度有效逼近任何一个非线性过程[14],因此,确定神经网络层数为1个输入层、1个隐含层和1个输出层.神经网络控制器的输入参数包括制冷站系统EER、影响EER的室外环境参数、负荷以及与阈值有关的-1,具体为以下7个:1)室外温度Tto[k];2)室外湿度Tho[k];3)当前时刻系统提供冷量Qch[k];4)当前时刻系统能效比EER[k];5)下一时刻负荷预测值Qpred[k+1];6)EER设定值EERset[k];7)-1.输出参数为冷冻水供水温度Tchwset[k]、冷却塔风机频率ftower[k]、冷冻水泵频率fpumpch[k]、冷却水泵频率fpumpc[k].
采用式(18)的经验公式法[15]确定神经网络控制器隐含层神经元个数
其中:l为隐含层单元数,n为输入单元数,m为输出单元数,a为[1,10]之间的常数.通过试凑,选择隐含层神经元数量为10.
3.5 神经网络预测控制器在线优化
制冷站采样周期为5分钟,取预测时域M=6,预测末来半小时系统的状态,设置学习率µ=0.1.神经网络预测控制器在线优化按照以下步骤进行:
1)初始化神经网络控制器的权值,将W设为较小的随机数(0.01或更小),初始化优化目标函数中∆EER,∆Q为0;
2)根据制冷站实际输出反馈值x[t0]确定系统预测时域内的状态初值x[t1];
3)设当前时刻为k=t1,设置EER期望输出x∗[t1+i](i=1,2,···,M)在预测时域内各时刻的值;
4)根据负荷预测模型得到负荷预测值Qpred[k],由当前能效比EER[k]与设定值EERset[k]得到∆EER,由当前时刻系统供冷量Qch[k]与需求冷量Qpred[k]得到∆Q,通过权重自适应模块得到权重因子α[k],更新优化目标函数的权重因子;
5)将x[t1]和x∗[t1+1]输入给神经网络控制器,得到控制量在预测时域内的初始值u[t1],根据负荷预测模型得到负荷预测值Qpred[t1],再将控制量u[t1]、状态变量x[t1]和负荷Qch[t1]等作用于能效比预测模型,得到预测值[t1+1];
7)重复上述步骤5)–6),然后根据正则方程(14)–(15),递推计算拉格朗日乘子向量λ[k]和q[k];
8)根据第7)步计算得到的拉格朗日乘子q[k]的值,基于随机梯度下降法修正神经网络控制器权值.权值更新过程如式(19)–(20)所示,即
其中W是神经网络控制器的权值矩阵;
9)重复上述步骤5)–8),对神经网络控制器权值进行修正,直至神经网络收敛,理想情况下∆W=0;
10)令t1=k+1,重复上述步骤3)–9),计算出各采样时刻的最优控制量u,直至控制过程结束.
上述神经网络在线优化策略通过多步预测,将制冷站时变、大滞后等动态特性完全融进有限时域的滚动优化目标中,增强了系统的鲁棒性,同时利用优化过程中测量到的系统信息进行反馈校正,使模型有效克服参数时变特性所带来的扰动影响.
下面对算法的计算量和占用存储空间量进行分析.假设状态变量有n个,控制量有m个,神经网络控制器权值有nw个,则在预测控制系统寻优过程中,所提出的预测控制滚动优化算法需要进行约(2n(n+m)+nw(m+2))M步迭代计算,占用(n+m)M+2nw个计算机存储单元,说明算法计算量和占用存储单元数与n,m,nw呈线性关系,而传统非线性规划算法在求解过程中计算量和占用存储单元数与状态、控制变量维数指数相关,会导致“维数灾”问题,不易工程实现.因此,在进行滚动优化求解时,提出的神经网络预测控制优化算法具有计算量小、占用存储空间少的优势,可以采用低成本的基于ARM(Advanced RISC Machines)内核的现场控制器实现.
4 实验研究
4.1 研究对象概况
以广东省某公共建筑制冷站为研究对象,该建筑总面积约66280 m2,空调区域面积约占37544 m2,制冷站各设备详细信息见表2.
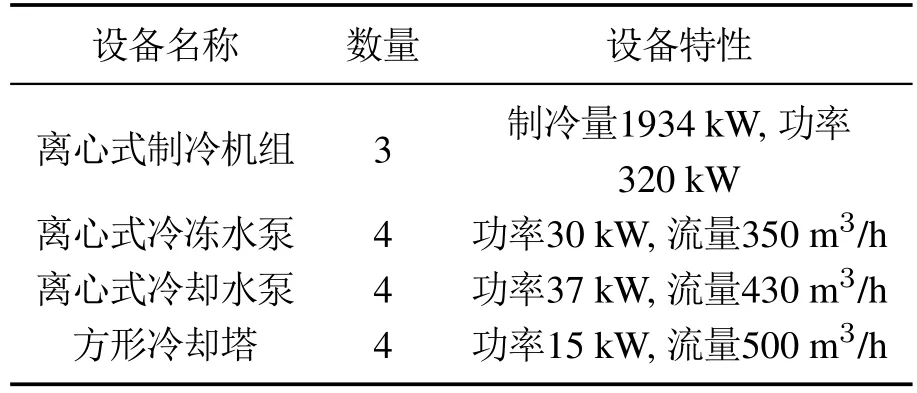
表2 制冷站设备Table 2 The air-conditioning refrigeration equipment
4.2 预测模型构建
制冷站控制目标为在满足建筑冷负荷需求的前提下,使系统整体能效比达到期望值,因此需要构建准确的负荷预测模型及系统能效比预测模型.制冷站所具有的结构复杂、非线性、强耦合等特点,给机理建模带来了困难.相比之下,神经网络算法无需繁冗的建模过程,且模型精度较高,在非线性系统建模方面更具优势[16].因此,采用神经网络构建系统负荷预测模型和能效比预测模型.
4.2.1 数据采集与预处理
仿真实验通过在该公共建筑现场安装的传感器采集数据,采样周期为5 min.选取2020年9–10月的6335条实测样本数据对负荷预测模型和能效比预测模型进行建模,通过传感器所测得的供回水温度计算出建筑冷负荷,通过测得的系统功率、冷冻水泵频率、冷却水泵频率及冷却塔风机频率计算出系统能效比.由实测数据计算所得的建筑冷负荷分布情况、系统整体EER分布情况分别如图3–4所示,可以看出,冷负荷波动幅度较大且具有较为明显的周期性变化规律.EER大多分布在3.6左右,只有极少数达到4.6,系统整体EER偏低.
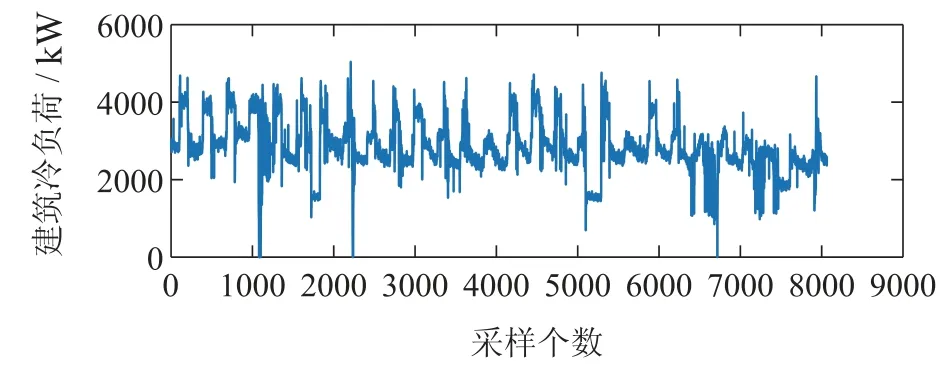
图3 建筑冷负荷分布情况Fig.3 Distribution of building cooling load
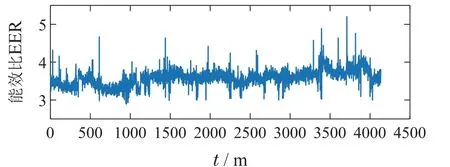
图4 原控制系统EER分布情况Fig.4 EER distribution of the original control system
为了消除尖峰噪声和各种随机噪声的影响,采用滑动平均滤波算法[17]对原始数据进行处理.首先设定滑动队列长度N,每次获取一个新数据放入队尾,并去除原来队首的一个数据,依次对队列中的N个数据进行算术平均运算,获得新的滤波结果.对建筑冷负荷、室外温湿度、水泵及风机频率等原始数据进行平滑滤波处理,通过反复实验设定队列长度N为24.以室外温度数据为例的滤波结果如图5所示.实验结果表明,该滤波方法可以平滑数据,获得最具有代表性的数据集合.
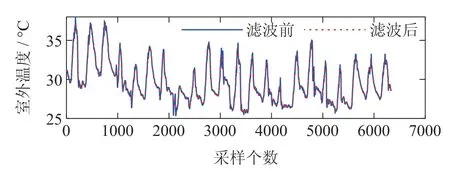
图5 室外温度滤波结果Fig.5 Outdoor temperature filtering results
4.2.2 神经网络结构及参数
Elman网络是具有局部记忆单元和局部反馈连接的递归神经网络,在前馈神经网络结构的基础上增加承接层,用来记录隐含层前一个时刻的输出值.承接层神经元的输出经延迟与存储,再输入到隐含层,使网络对历史数据具有敏感性,增强了动态处理能力[18].选用4层Elman神经网络建立制冷站预测模型,包含1个输入层、1个隐含层、1个承接层和1个输出层.将实测样本数据划分为训练集和测试集,数据占比分别为70%和30%.由于数据的规模较小且周期性强,因此每批次都将所有训练数据送入神经网络进行训练,在保证网络计算时间的前提下满足精准的负荷预测及EER预测需求.
建筑冷负荷受多重因素影响,包含由室内人员及电器引起的室内区域温湿度变化、室外干湿球温度、太阳辐照程度、风速等[19].另外,历史负荷表示负荷需求的潜在规律,也会对建筑冷负荷造成影响[20].因此,确定负荷预测模型的输入参数为室外温度Tto[k]、室外湿度Tho[k]、当前时刻负荷值Qch[k]、前一天负荷值Qdayago[k]和前一周负荷值Qweekago[k],输出参数为下一时刻的负荷预测值Qpred[k+1].
系统能效比预测模型的输入是影响系统EER的状态变量和控制变量.选取室外温度Tto[k]、室外湿度Tho[k]和系统当前负荷Qch[k]作为模型状态变量输入,选取冷冻水供水温度设定值Tchwset[k]、冷冻水泵频率fpumpch[k]、冷却水泵频率fpumpc[k]、冷却塔风机频率ftower[k]作为模型控制变量输入.输出变量为下一时刻系统能效比EER[k+1].
网络隐含层神经元数目对预测模型的性能有显著影响.Elman网络结构中,由于承接层需要对隐含层的输出进行记录并存储,因此其神经元个数与隐含层神经元个数相同.基于式(18)确定隐含层神经元个数,采用不同神经元个数得到的预测模型均方误差如表3所示,当隐含层神经元个数为8时,负荷预测模型的均方误差最小,当隐含层神经元个数为9时,EER预测模型均方误差最小.因此,确定负荷预测模型和EER预测模型隐含层(承接层)神经元个数分别为8和9.
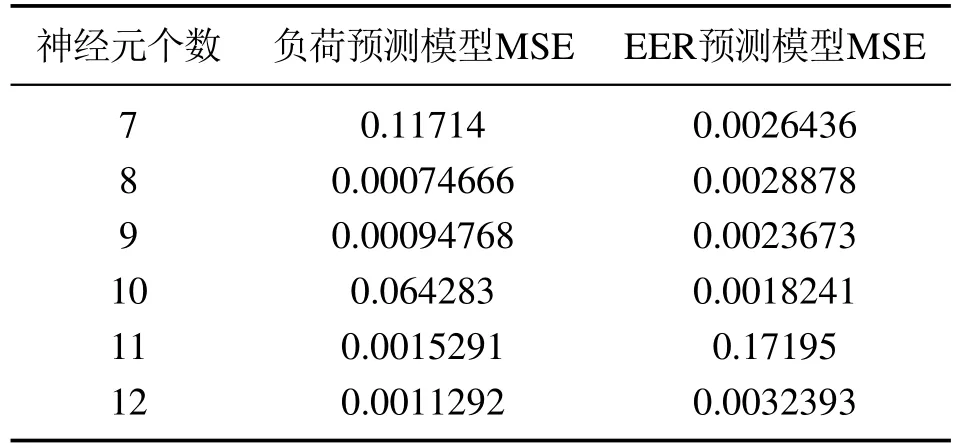
表3 不同情况下预测模型的均方误差Table 3 MSE of prediction model under different conditions
训练函数是影响网络性能的主要因素之一,反向传播(back propagation,BP)算法是最常用的算法,它使用梯度下降法来寻找极小值,然而其收敛速度较慢[21].Traingdx 为带自适应学习率和动量因子的梯度递减法,它根据误差性能函数来调节学习率大小,解决了一般BP算法中学习率大小选择不当的问题[22],提高了收敛速度并增加了算法的可靠性.因此,采用Traingdx算法对神经网络进行训练,动量因子为0.9.
学习率决定每一次循环训练中所产生的权值变化量.学习率过大导致系统不稳定,过小将会增加训练时间.经过实验发现,学习率取0.1时预测模型训练结果的均方误差较小.因此,设定学习率的初始值为0.1,并分别设置学习率增长比、下降比为1.05与0.7,在后续的训练中自动调节学习率的大小.
传递函数又称激活函数,输入层到隐含层的激活函数选用tansig正切函数,隐含层到输出层的激活函数选用Pureline线性函数.
4.2.3 预测模型训练
利用测试集数据对预测模型建模结果进行验证,预测结果如图6 所示,其中,横坐标为测试样本编号,实线为经过滤波后的采样值,虚线为预测值.经计算,负荷预测模型均方误差为159.087201 kW,相对误差在±5%之内,EER预测模型均方误差为0.00124,相对误差在±3%之内,满足工程需要.
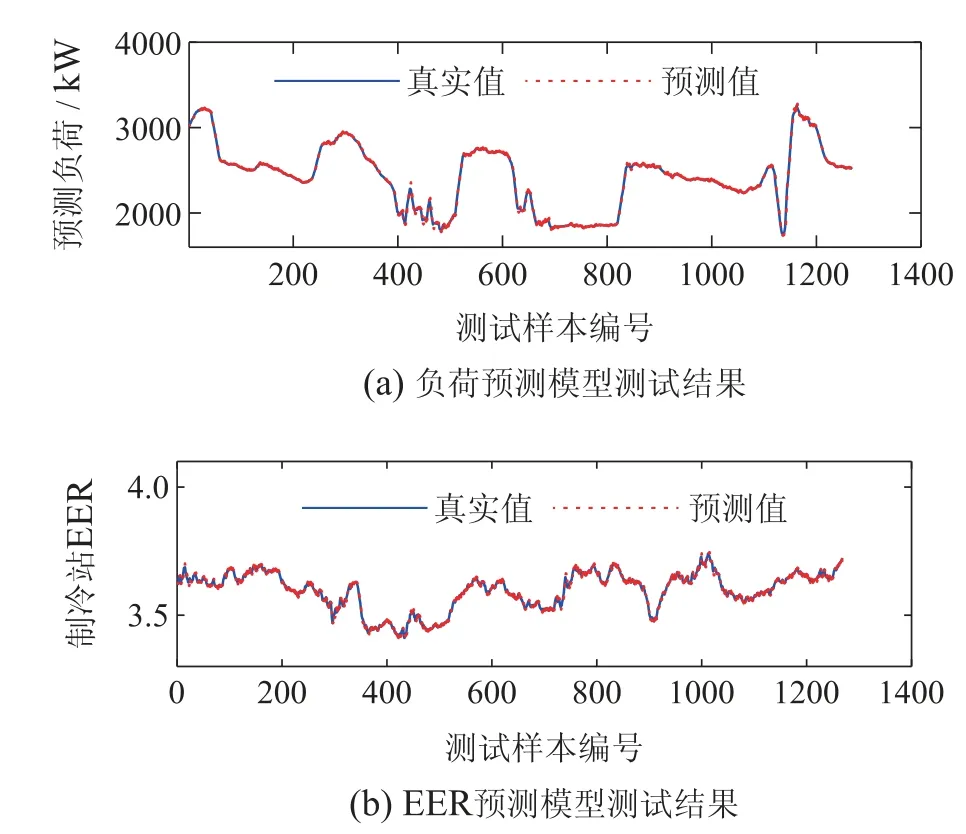
图6 预测模型测试结果Fig.6 Predictive model test results
4.3 制冷站预测控制仿真实验
为了进行控制效果对比实验,首先只采用所提出的神经网络预测控制算法对制冷站进行控制,未加入优化目标权重自适应模块,此时α取固定值0.7.设置EER初始值为3.5,为了探究神经网络控制器的控制效果,在系统运行至75 min时,将EER设定值改为4.6,EER跟随情况如图7(a)所示.可以看出,在满足负荷需求的前提下,控制器能够使EER实时跟踪设定值,提高系统能效.系统提供冷量动态变化过程如图7(b)所示,可以看出在绝大部分时间范围内,系统输出冷量大于需求冷量(负荷).
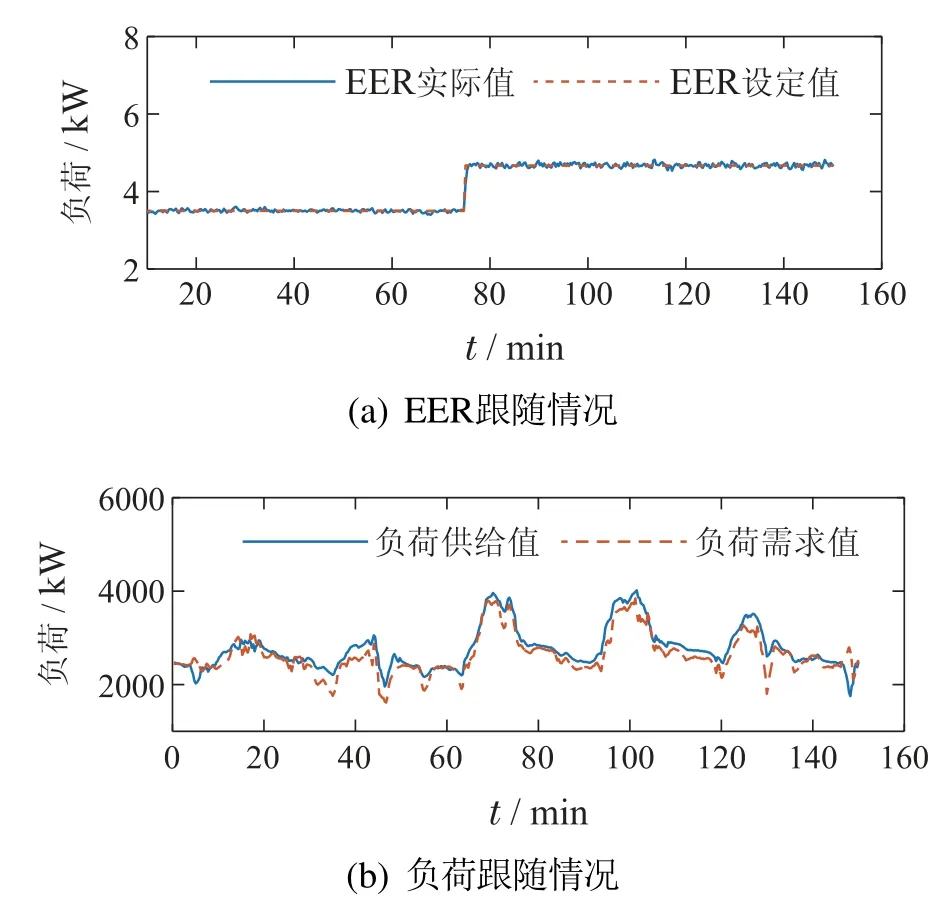
图7 预测模型测试结果Fig.7 Predictive model test results
图8为施加控制策略后设备性能变化.在第75 min提高EER 设定值后,图8(a)所示的冷冻水供水温度由8.56◦C变为12.25◦C,由第2.2.4小节可知在满足冷量需求时提高冷冻水供水温度,可提高制冷机组能效比;图8(b)所示的冷冻水泵频率由43.56 Hz降至41.52 Hz,水泵能耗减少;图8(c)所示的冷却塔风机频率由35.12 Hz变为43.02 Hz,风机频率增加使得冷却水回水温度下降,制冷机组能效提高;图8(d)所示的冷却水泵频率由42.89 Hz 变为47.62 Hz,此时冷却水流量增加,制冷机组冷凝压力、压缩机吸排气温度均降低,功耗下降,达到节能目的[23].
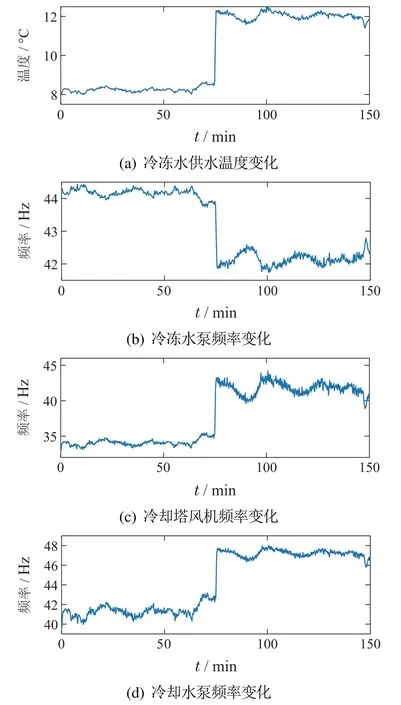
图8 设备性能变化Fig.8 Equipment performance changes
综上可知,神经网络预测控制策略相较于原PID控制系统而言,能效比均值由3.5 提高至4.6,提升约32.5%,能够用于实际制冷站的节能优化控制.
4.4 基于优化目标权重自适应的预测控制实验
在系统运行至第48 min时,加入权重自适应模块对其进行控制,负荷需求量的变化导致权重因子α随之改变,变化情况如图9所示.系统能效比也随之发生改变,能效比均值由48 min前的4.6提高至48 min后的4.919,能效比提升约6.93%,其变化情况如图10所示.制冷站供给冷量和需求冷量(负荷)变化曲线如图11所示.与图7(b)相比,在加入权重自适应模块后,制冷站制备的冷量变少,制备冷量更贴合需求冷量(负荷),进一步提升了系统能效.
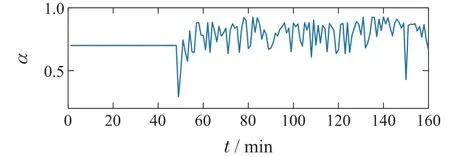
图9 权重因子α变化曲线Fig.9 The change curve of the weighting factor α
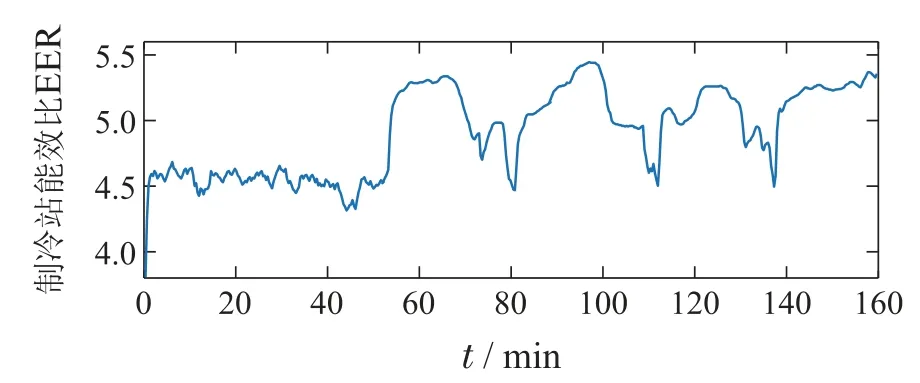
图10 EER变化曲线Fig.10 EER change curve
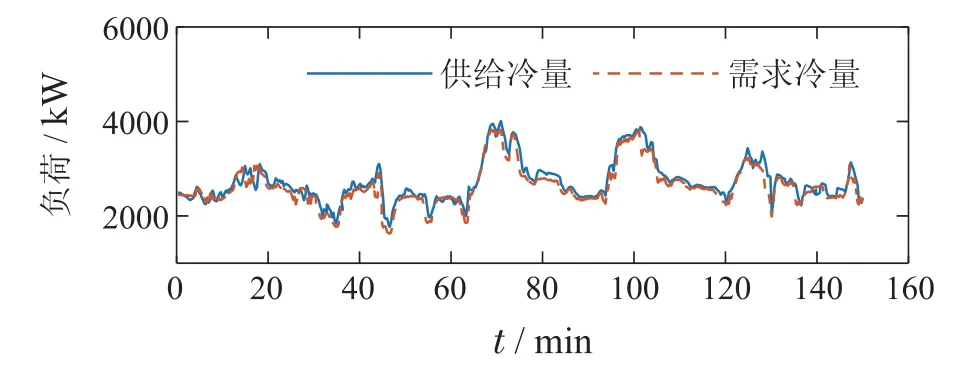
图11 加入权重自适应模块后负荷变化情况Fig.11 Load change after adding weight adaptive module
5 结论
以满足建筑冷量需求、提高系统整体能效为目标,提出了一种制冷站双目标权重自适应非线性预测控制策略.结合多步预测、在线滚动优化和反馈校正策略,采用3层前馈神经网络作为优化反馈控制器,将系统优化目标函数作为神经网络控制器在线寻优性能指标,基于变分法和随机梯度下降法对控制器权值进行在线寻优,提升了系统的鲁棒性;且所提出的神经网络预测控制滚动优化算法与非线性规划算法相比计算量小、占用存储空间适中,能够克服非线性规划算法的“维数灾”问题,易于工程实现.此外,为解决满足建筑冷量需求和提高系统能效两个优化目标之间的冲突问题,设计了基于模糊逻辑的优化目标权重自适应模块.仿真实验结果表明,采用所提出的双目标权重自适应非线性预测控制策略后,制冷站能够在负荷不断变化的情况下维持高能效比工况,在未加入优化目标函数权重自适应模块时,非线性预测控制策略的平均能效较PID控制提高约32.5%,在此基础上,将权重因子引入预测控制优化目标函数,可以将制冷站能效比在PID控制基础上提高约39.43%.
本文所提出的控制策略在用于制冷站控制时取得了良好的节能效果,但是由于实验条件和时间方面的限制,还需要在以下方面对控制策略做进一步研究:1)进行模型的可移植性分析,在实际项目中对模型进行在线修正;2)设计变论域模糊逻辑,通过变论域方法实现输入、输出论域的动态调整,以进一步增强控制系统自适应能力,提升系统性能.

