具有输入输出约束的无人直升机预设性能安全跟踪控制

马浩翔 陈 谋 吴庆宪

(1.南京航空航天大学自动化学院,江苏 南京 211106;2.河南科技大学信息工程学院,河南 洛阳 471023)

1 引言

由于无人直升机具有垂直起降和定点悬停等优势,且已广泛应用于各种民用和军用领域,如未知环境探测[1]、物资吊装[2]等.但无人直升机具有欠驱动及各通道高度耦合的特性,其有效控制存在很大挑战.国内外学者对相关建模方法和控制技术均做了大量研究,并取得了许多成果[3–7].然而,无人直升机的多数任务常伴随有多种约束[8–9],因此,在考虑多约束情况下无人直升机的安全控制问题具有十分重要的意义.

由于无人直升机自身物理条件的限制,其主旋翼拉力及控制力矩都会不可避免地受到饱和约束.针对非线性系统的抗饱和方法已取得了许多有效的研究成果,如模型预测控制方法[10]、双曲正切函数方法[11]与辅助系统方法[12]等.文献[13]通过双曲正切函数来代替输入饱和函数,并设计了自适应跟踪控制器保证系统全局稳定.除此之外,文献[14]通过一类Sigmoid函数去处理输入饱和特性,并对估计误差采用模糊逻辑系统补偿,以实现闭环系统的稳定.

除输入饱和约束外,在特定的任务环境下,无人直升机常常受到外部环境的限制,这类限制会表现为航迹约束[15];另外,考虑到无人直升机在实际控制中会对飞行姿态有较高的限制,这类限制表现为姿态角约束[16].近年来,学者们针对无人直升机的输出受限问题做了大量研究,常用的方法有模型预测控制方法、障碍Lyapunov函数方法与预设性能函数方法等.为保证直升机系统在预设姿态角约束下的瞬态与稳态性能,文献[17]设计了一种有限时间预设性能控制器.文献[18]将预设性能函数与容错控制方法相结合,针对无人直升机的姿态与高度系统提出了一种自适应容错受限控制方法.然而,障碍Lyapunov函数方法与预设性能函数方法在处理受限问题时,都要求预设的期望跟踪信号始终在预设的约束内.但在许多复杂环境下,这些约束往往是时变且无法提前预测的,只能通过直升机自带雷达[19]或其他传感器[20]实时获取.正是由于实时约束无法预知,预设的期望跟踪信号很有可能与实时约束发生冲突,并导致撞到障碍物等不可逆的后果.因此,如何在保证安全性能的前提下,尽可能地实现对预设期望跟踪信号的跟踪,是一个亟待解决的问题.

另外,未知外部干扰广泛存在于无人直升机的实际飞行过程中,并会影响系统稳定性.尤其在输入输出约束下,严重的干扰更是会造成无人直升机的飞行不稳定甚至坠机等不可逆的后果.一直以来,各种抗干扰控制方法,如自适应控制方法[21]、扩张状态观测器方法[22]、干扰观测器方法[23]等,在直升机系统中得到了广泛应用.针对无人直升机系统中合外力与力矩上的复合干扰,文献[24]设计了一种非线性自适应律,并通过仿真对其有效性进行了验证.文献[25]采用参数自适应方法对外部干扰的未知上界进行估计,并结合反步控制方法实现了对干扰的抑制并保证了闭环系统的稳定.

受以上工作的启发,本文在考虑姿态与高度约束的情况下,基于一类边界保护算法,构建了新的安全期望跟踪信号.为保证无人直升机姿态与高度系统的安全性,将预设性能函数与边界保护算法进行结合,并对跟踪误差进行转换.针对系统的输入饱和现象,使用Sigmoid函数进行逼近;同时,针对饱和函数的逼近误差与未知外部干扰构成的复合干扰,采用参数自适应方法对其上界进行逼近,并基于反步控制方法设计控制器.然后,通过Lyapunov方法证明了闭环系统所有信号的收敛性,保证了无人直升机在输入输出约束下的安全跟踪性能.最终,通过数值仿真验证了所提控制方法的有效性.

2 建模与问题描述

2.1 无人直升机姿态与高度系统模型

考虑无人直升机的机体运动学及动力学特性,其姿态与高度系统模型[3]可表示为

式中:ϕ为滚转角,θ为俯仰角,ψ为偏航角,Z为飞行垂直高度;p为滚转角速度,q为俯仰角速度,r为偏航角速度,v为垂直方向上的速度;Ix,Iy及Iz为无人直升机的转动惯量分量;Σ1,Σ2及Σ3分别表示无人直升机在x轴、y轴、z轴3个方向的总控制力矩,Tmr为主旋翼拉力;dx,dy,dz及dT为无人直升机受到的未知外部干扰;m为无人直升机的质量,g为重力加速度.

考虑到无人直升机自身物理特性的限制,其主旋翼拉力及控制力矩都会受到饱和约束,为此将主旋翼拉力的饱和函数表示为[11]

与式(2)类似,每个方向上控制力矩的饱和函数也可表示为

为方便控制器的设计,首先定义Ω=[p q r]T,J=diag{Ix,Iy,Iz}为惯性矩阵[3],以及姿态变换矩阵[3]为

则可将系统(1)重新表述为如下二阶系统:

式中:x1=[ϕ θ ψ Z]T与x2=[p q r v]T为系统状态量;d=[dx/Ixdy/Iydz/IzdT/m]T=[d1d2d3d4]T为未知外部干扰;y为无人直升机姿态与高度系统的输出;u=[u1u2u3uT]T为饱和作用下的控制输入;f1,f2,g1与g2可表示为

通过定义系统不考虑饱和下给定控制输入向量U=[Σ1Σ2Σ3Tmr]T,可得给定控制输入与饱和作用下的控制输入的差值向量表达式为

2.2 问题描述与相关假设

考虑到无人直升机在实际飞行中存在最小转弯半径、最大爬升率以及实时外部环境等限制,无人直升机常常受到实时高度约束与姿态角约束.定义系统的实时上界值为yup(t)=[ϕup(t)θup(t)ψup(t)Zup(t)]T,实时下界值为ylow(t)=[ϕlow(t)θlow(t)ψlow(t)Zlow(t)]T.由于约束的实时性,预设的期望跟踪信号yd(t)=[ϕd(t)θd(t)ψd(t)Zd(t)]T就有可能会超出边界值.此时,无人直升机控制将优先考虑其安全问题.综上所述,本文控制目标如下.

设计预设性能安全跟踪控制器使得无人直升机系统在满足输入输出约束条件的基础上,尽可能地跟踪原期望跟踪信号yd,同时,保证闭环系统中的所有信号有界.

注1本文基于传感器得到的边界信息采样点,结合相关平滑方法,如B样条曲线方法、插值拟合方法等,进行处理得到实时输出约束,具有实时性、平滑性和有界性.

为了实现控制目标,引入以下定义、引理与假设.

定义1[14]给出Sigmoid函数S(x)表达式如下:

式中a1,a2与a3分别为与幅值、增益和偏移相关的待设计常数.Sigmoid函数式(6)是一个不含奇异点的连续可微函数,且其泰勒级数是收敛的.

引理1[12]以h为输入信号,构建以下指令滤波器:

式中:λ(0)=h(0),η(0)=0.如果h满足||≤σ1以及||≤σ2,其中σ1,σ2>0,则对∀δ >0,存在Γ >0,ζ ∈(0,1],使得|λ-h|≤κ成立,且||及||是有界的.

引理2[12]对任何ξ >0以及e ∈R,都有以下不等式成立:

式中o=0.2758.

引理3[13]对于无人直升机系统(4),如果存在一阶连续可微的函数V(x1,x2)与C0>0,ε0>0满足下面的条件:

1)V(x1,x2)的初值是有界的;

2)κ1(∥x1∥,∥x2∥)≤V (x)≤κ2(∥x1∥,∥x2∥);

式中κ1,κ2:Rn →R为K类函数,则系统的解x1(t),x2(t)最终一致有界.

假设2[23]无人直升机未知外部干扰信号d(t)满足范数有界条件,即满足|di|≤εd,i,其中εd,i >0,i=1,2,3,4.

假设3[4]无人直升机的滚转角与俯仰角一直在限定区间内变化,即ϕ∈(-π/2,π/2),θ∈(-π/2,π/2).

假设4[4]无人直升机的所有信号均是可测的,且初始状态均在初始输出约束范围内.

假设5[11]针对输入饱和、输出约束与外部干扰下的无人直升机系统(4),存在切实可行的控制器能够跟踪预设期望跟踪信号,同时,保证系统的稳定性与安全性.换言之,输入饱和作用所引起的差值向量∆u必然是范数有界的.

注2结合无人直升机系统(4)与式(5)可知,虽在输入饱和的作用下,给定的输入信号与实际输入信号间有差值,但该误差不能太大,否则很难获得一个可行的控制方案来保证无人直升机的稳定性与安全性.因此,假设5是满足实际系统要求的.

3 安全期望跟踪信号生成与误差转换

本节在考虑无人直升机输出约束的情况下,采用一类边界保护算法构建新的安全期望信号.为了保证系统对于安全期望跟踪信号的跟踪性能,采用了预设性能函数对跟踪误差进行转换,将输出约束下的安全跟踪控制问题转换为无约束跟踪控制问题.基于预设的期望跟踪信号yd(t)∈Rm以及其实时输出约束yup(t),ylow(t),边界保护算法的计算步骤归结如下:

步骤1根据预设期望跟踪信号与实时的边界信息,计算出严格在输出约束内的受限期望跟踪信号yc(t);

步骤2通过指令滤波器对yc(t)进行滤波,得到光滑的安全期望跟踪信号ys(t);

步骤3采用误差性能转换函数将输出约束下的安全跟踪控制问题转换为无约束跟踪问题.

3.1 受限期望跟踪信号yc(t)的生成

在不失一般性的情况下,以滚转角ϕ为例,定义一个实时裕量

式中ρϕ >0为待设计的裕量参数.

为保证裕量有下界,在式(9)的基础上定义算法所用到的实时边界裕量∆ϕ(t)形式如下:

式中Mϕ >0为与后文预设性能参数相关的待设计下界值.根据式(10),将∆ϕ(t)的一阶和二阶分段导数设计为

式中k=1,2.

注3∆ϕ(t)及其一阶、二阶分段导数的具体形式分别由式(10)与式(11)给出,且均为分段可微的.下文需要用到∆ϕ(t)的导数信息时,无需对式(10)进行求导,而是直接由式(11)生成.

式中k=0,1,2.另外,为保证系统初始跟踪误差为零,设计ϕc的初值信号要求如下等式成立:

同理,针对于系统(4)的另外3个输出:俯仰角θ、偏航角ψ和垂直高度Z,通过设计合适的下界值Mθ >0,Mψ >0,MZ >0,都可生成对应的实时边界裕量∆θ(t),∆ψ(t),∆Z(t)与受限期望信号θc(t),ψc(t),Zc(t).则对于任意时间t≥0,每个受限期望跟踪信号ϖc(t),ϖ ∈{ϕ,θ,ψ,Z}均严格保持在对应的实时输出约束区间[ϖlow(t),ϖup(t)]内,且始终与边界保持着最小距离Mϖ.换言之,始终有如下不等式成立:

式中ϖ ∈{ϕ,θ,ψ,Z}.

由式(14)可知,系统受限期望跟踪信号yc(t)=[ϕc(t)θc(t)ψc(t)Zc(t)]T及其一阶导数与二阶导数均有界,即存在常数εc,k >0,k=0,1,2 使得≤εc,k成立.

3.2 安全期望跟踪信号ys(t)的生成

为了对上节得到的受限期望跟踪信号进行平滑处理,本节以yc为输入,参考引理1设计了如下形式的指令滤波器[12]:

式中:η ∈R4为辅助向量,Γ ∈R4×4及ζ ∈(0,1]分别为待设计的正定对角矩阵与常数,并选择初值ys(0)=yc(0).

由引理1可知: 通过选择合适的参数Γ和ζ,指令滤波器(15)的跟踪误差可以收敛到任意小的邻域内,即存在任意常数εs >0满足

结合式(14)(16)可得

式中=Mϖ+εs,ϖ ∈{ϕ,θ,ψ,Z}.

3.3 预设性能函数设计与误差转换

基于上述输出约束,首先,定义安全跟踪误差信号

式中e0=[eϕ eθ eψ eZ]T.

注4针对于跟踪误差的初值问题,结合式(13)与设计的指令滤波器(15),可知y(0)=yc(0)=ys(0),即e0(0)=0.

由式(14)可知,为保证系统输出y一直满足实时输出约束,只需要使得安全跟踪误差信号始终小于实时边界裕量的最小值.因此,本文引入预设性能函数控制方法,通过对安全跟踪误差信号添加预设性能约束,以保证闭环系统的瞬态跟踪性能.

不失一般性,仍以滚转角ϕ为例,若如下不等式约束成立,系统的安全跟踪性能将得以保证:

结合式(19),可定义无人直升机滚转角误差的预设性能函数形式为

考虑式(20),则保证直升机系统的安全性不等式约束(19)可改写为

为实现上述性能指标(21),采用如下形式的误差性能转换函数:

式中:βϕ(t)为转换后的无约束滚转角误差变量,Pϕ(t)=Pϕ,up(t)-Pϕ,low(t).则对βϕ(t)关于时间t求导可得

类似地,可以得到其余无约束误差βθ(t),βψ(t)及βZ(t).通过定义无约束误差向量β=[βϕ βθ βψ βZ]T及预设性能向量Pup=[Pϕ,upPθ,upPψ,upPZ,up]T,Plow=[Pϕ,lowPθ,lowPψ,lowPZ,low]T,结合无人直升机姿态与高度系统(4),β关于时间t的导数可以写成

最后,将输出约束下的无人直升机安全跟踪控制问题转化为了如下形式系统的跟踪控制问题:

4 控制器设计与稳定性分析

本节针对前文得到的系统(25),结合反步法设计自适应抗饱和控制器.针对系统的输入饱和现象,采用Sigmoid函数进行逼近;同时,针对饱和函数的逼近误差与未知外部干扰构成的复合干扰,采用参数自适应方法对其上界进行逼近.其控制设计流程由图1给出,其中,=[Mϕ(t)Mθ(t)Mψ(t)MZ(t)]T,为参数的自适应估计值.

图1 无人直升机预设性能安全跟踪控制流程图Fig.1 Control Diagram of the prescribed performance safe tracking controller for unmanned helicopter

4.1 输入饱和处理

首先,基于定义1中的Sigmoid 函数(6),给出控制饱和输入Tmr的估计函数表达式如下[14]:

式中选取Sigmoid函数中的参数为a1=2,a2=a3=1.

定义饱和输入(2)与估计函数(26)的误差为

类似地,针对其余饱和下的控制输入分别设计估计函数如下:

并使得误差信号∆ωi=ui(Σi(t))-ωi(Σi(t))满足如下不等式:

定义估计向量ω=[ω1ω2ω3ωT]T,误差向量∆ω=[∆ω1∆ω2∆ω3∆ωT]T与误差上界向量ħ=[ħ1ħ2ħ3ħT]T,则有以下等式成立:

结合系统(25)与式(30)构建有上界的复合干扰D=g2(x1,x2)∆ω+d.根据假设5,式(27)(29)与g2(x1,x2)形式可知,D是范数有界的.换言之,对于D(t)=[D1(t)D2(t)D3(t)D4(t)]T,存在εDi >0,使得

成立.因此,引入估计函数(26)(28),系统(25)可进一步表示为

4.2 自适应安全跟踪控制器设计

定义如下误差变量:

式中:x2d表示待设计的虚拟控制律,λu为引入的辅助系统信号,其系统动态形式如下[14]:

根据系统(32)–(34),对e1关于时间t求导得

设计虚拟控制律x2d为

式中K1为待设计的正定矩阵.

选取如下形式的Lyapunov函数:

根据式(36)–(38),对W1关于时间t求导可得

为了求得虚拟控制律x2d的可用导数,令x2d通过以下形式的一阶滤波器[7]:

式中:λ2∈R4为x2d的估计值,τ2∈R4×4为待设计的正定对称矩阵.

式中:Mλ2(e1,,,λu)为紧集Nλ2(e1,,,λu)上的光滑函数向量.结合式(17),假设1与假设4可知,在给定的初始条件下,函数Mλ2(·)在紧集Nλ2(·)上是有界的,即满足∥Mλ2∥≤εM,式中有εM >0.

根据式(32)(34)(41),对e2关于时间t求导得

为抵消未知复合干扰带来的影响,基于式(31),定义复合干扰D的上界向量Ξ=[εD1εD2εD3εD4]T,及其估计向量∈R4.选择如下形式的Lyapunov函数:

式中e2i,i=1,2,3,4表示e2的第i个误差变量.

结合引理2,有如下不等式成立:

式 中: Tanhe2=diag{tanh(e21/ξ1),tanh(e22/ξ2),tanh(e23/ξ3),tanh(e24/ξ4)},ξ=o[ξ1ξ2ξ3ξ4]T.由引理2可知,必然有ξi >0 为待设计的常数且o=0.2758.

结合系统(32)与滤波器(40),设计控制向量为

式中K2∈R4为待设计的正定对称矩阵.

针对式(46)中估计向量设计如下自适应律:

式中µ>0为待设计的常数.

考虑如下Young不等式:

并将式(46)–(47)代入式(44)中可得

4.3 稳定性分析

本节将基于所设计控制器,对无人直升机姿态与高度闭环系统进行稳定性分析.为方便表述,定义

综合上述安全期望跟踪信号的生成过程与自适应安全跟踪控制器的设计思路,可得到如下定理.

定理1考虑同时存在未知外部干扰、输入饱和、姿态与高度约束的高度姿态复合模型(1).设计安全期望跟踪信号为式(12),误差性能转换函数为式(22),并设计参数自适应律为式(47),虚拟控制律为式(37),及实际控制输入为式(46).若系统输出的初始状态在实时输出约束内,且在所设计控制器参数满足不等式C >0,则无人直升机闭环系统能够在跟踪安全期望跟踪信号ys的基础上,保证所有信号最终一致有界,并始终满足实时约束.

证取Lyapunov函数为

结合式(39)(49),对W关于时间t求导可得

对式(52)关于时间t积分可得

通过选取合适参数K1,K2,τ2,Λ,µ以保证C >0,根据最终一致有界理论,可知闭环系统所有信号均有界,且满足安全跟踪性能(21).结合所设计的安全期望跟踪信号特性(17),系统始终满足实时约束.

证毕.

5 数值仿真

本节主要对所设计的无人直升机预设性能安全跟踪控制器的有效性进行验证.首先,给出无人直升机姿态与高度系统的相关参数如表1所示[4].

表1 中型无人直升机参数Table 1 Parameters of the medium-scale UAH

在本仿真算例中,设定无人直升机的初始姿态为Ω(0)=[5.7-11.5 0]T(◦),初始高度为Z(0)=350 m.原期望参考信号分别设为

外部干扰设定为

安全期望跟踪信号计算过程中的相关参数选取为Mϕ=0.05 rad,Mθ=0.08 rad,Mψ=0.03 rad,MZ=35 m,Γ=diag{10,10,10,10},ζ=0.2.预设性能参数选取为Pup(0)=[0.05 0.08 0.03 35]T,Plow(∞)=0.4Pup(0)以 及lϕ=lθ=lψ=lZ=0.1.控制器设计中的相关参数选取为K1=diag{12,4,15,2},K2=diag{10,10,10,5},τ2=diag{0.1,0.1,0.1,0.1},Λ=diag{1,1,1,1},µ=10.在此基础上,仿真结果在图2–8中给出.

图2 约束下的滚转角跟踪响应曲线图Fig.2 Tracking response of the roll angle with constraints

图3 约束下的俯仰角跟踪响应曲线图Fig.3 Tracking response of the pitch angle with constraints

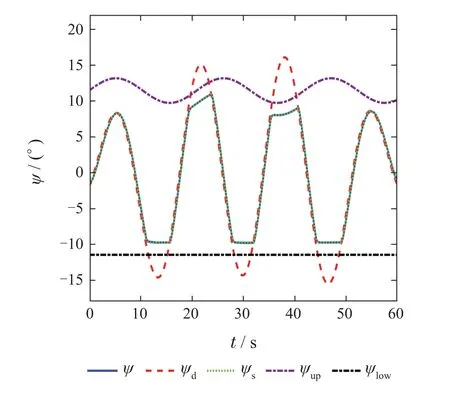
图4 约束下的偏航角跟踪响应曲线图Fig.4 Tracking response of the yaw angle with constraints

图5 约束下的垂直高度跟踪响应曲线图Fig.5 Tracking response of the altitude with constraints

如图2–5所示,红色虚线为原期望跟踪信号,绿色虚线为生成的安全期望跟踪信号.在所设计的控制器下,闭环系统输出可以在保证直升机姿态与高度安全性能的前提下,尽可能地跟踪上原期望姿态与高度.

图6给出了基于预设性能的输出跟踪误差.由此可得在经过预设性能函数进行误差转化后,闭环系统输出的瞬态与稳态性能进一步得以保证.图7给出了姿态角速度与垂直速度响应的跟踪曲线.

图6 基于预设性能的输出跟踪误差响应曲线图Fig.6 Tracking errors of the outputs with prescribe performance

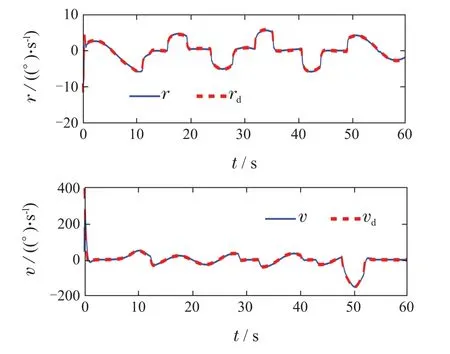
图7 姿态角速度与垂直速度跟踪响应曲线图Fig.7 Tracking response of the velocities of attitude angles and z-axis

图8给出了在输入饱和的约束下,系统在3个方向上的控制力矩与主旋翼拉力的响应曲线.由图2–8可知,在考虑实时输出约束与输入饱和的前提下,所设计的预设性能安全跟踪控制器可以保证无人直升机姿态与高度系统的瞬态性能与稳态性能.

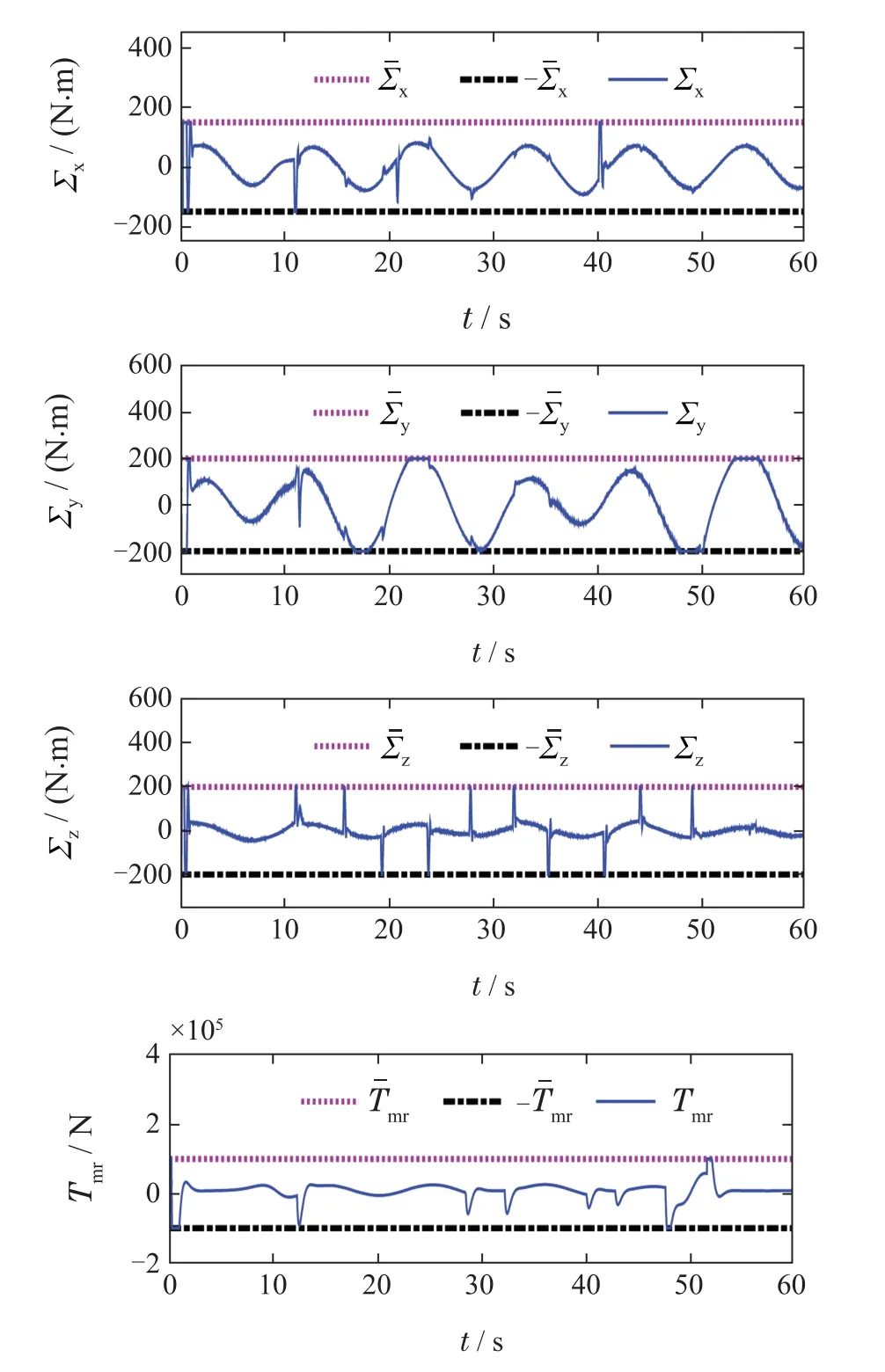
图8 饱和下的控制输入曲线图Fig.8 Responses of control inputs with saturation

综合上述仿真结果,本文所提的预设性能安全跟踪控制策略能够保证无人直升机系统在满足输入输出约束条件与安全性的基础上,尽可能地跟踪原期望跟踪信号,并保证闭环系统中所有信号的收敛性.

6 总结

本文针对输入输出约束下的无人直升机姿态与高度系统跟踪控制问题进行了深入研究.

1)首先,针对姿态与高度约束,通过设计一类边界保护算法,构建了新的安全期望跟踪信号.为保证系统对于安全期望跟踪信号的跟踪性能,将一类边界保护算法与预设性能函数方法相结合,在瞬态与稳态下均能保证系统的安全性;

2)其次,针对系统的输入饱和现象,使用Sigmoid函数进行逼近;同时,针对饱和函数的估计误差与未知外部干扰构成的复合干扰,采用参数自适应方法对其上界进行逼近,并基于反步控制方法设计了预设性能安全跟踪控制器;

3)最后,通过Lyapunov稳定性理论证明了闭环系统所有信号的收敛性并通过仿真加以验证.