混合热工和水力特性的风机盘管系统建模
赵安军 ,董菲菲 ,于军琪 ,张 宇 ,张萌芝
(1.西安建筑科技大学建筑设备科学与工程学院,陕西 西安 710055;2.西安建筑科技大学信息与控制工程学院,陕西 西安 710055)
1 引言
建筑能耗约占我国总能耗的42%,而空调系统能耗约占建筑能耗的60%[1].风机盘管系统作为公共建筑中最为常见的空调系统末端设备,运行效率不仅与机组本身及建筑室内外环境有关,而且与提供传热流体的制冷机房与热交换站紧密相关[2].相关工程实测数据表明,在确定的室内热舒适性要求下,风机盘管系统运行工况不仅影响其自身的能耗,同时也很大程度决定了制冷机房和热交换站的运行能耗[3].因此如何建立适用于实际工程、面向优化控制的风机盘管系统模型并提高风机盘管的运行效率使其能耗最低是空调系统节能的关键.
目前,国内外学者对风机盘管系统建模方法开展了较为广泛的研究,已经取得了一定的成果.Picon-Nunez等[4]针对冷却系统中冷却负荷的变化,建立了冷却系统热工水力性能模型,将冷却系统的热力学模型和水力模型相结合,该模型能够较好的适用冷却负荷的变化.Wang等[5]建议使用压降传感器来确定通过风机盘管的流量,然而由于需要大量昂贵的传感器和相应的安装成本,当应用于建筑中每一个风机盘管时,会带来成本上升和工期的延长.由世俊等[6]建立的非稳态水力模型给出了一种新的集中供热管网慢变流建模和数值求解方法,为动态水里特性的量化分析和精细化调节提供了支持.Kway等[7]研究出一种短期房间实时冷量需求预测方法,以应对不断变化的冷负荷,从而有效供冷及实现更优末端控制.胡泽宽等[8]介绍了动态压差平衡型电动水阀的工作原理,并指出在实际运行过程中电动水阀与风机盘管组合后,阀门开度与热输出特性之间成线性关系,所以采用流量与阀门开度之间为对数特性关系的电动水阀.Debashis等[9]采用数值方法研究了流量控制阀(旋转阀或电动电磁阀)的流量控制特性对通用型制冷机制冷性能的影响,并且给出了在不同等待周期和开度的情况下,水的质量流量随阀门开度的动态变化规律.殷平[10]介绍了电动水阀和空气换热器的流量特性,通过实验得出联立求解传热学公式无法得到广泛应用的换热器流量特性计算公式,电动水阀的等百分比流量特性会随阀权度和可调比的变化而变化.Mohammadian等[11–13]指出遗传算法(genetic algorithm,GA)、蚁群算法(ant colony optimization,ACO)、粒子群优化算法(particle swarm optimization,PSO)都是经典的优化问题数值解法,对于不同的问题有不同的优化目标,得到的最优解都是近似解.然而,GA算法收敛性能较差,寻找最优解所需的时间较长,PSO算法参数的选择过于随机,且算法搜索初期的收敛速度快,后期速度较慢.Wang和Zhu[14]针对供热管网,结合管网水力计算模型和基于遗传算法的管道阻抗标定模型,提出了一种基于水力计算模型的管网动态水力平衡优化控制方法.周璇等[15]借助图论的概念建立了管网的水力工况模型,并建立以系统能耗最小为目标,动态水力平衡为主要约束的管网系统优化调节的目标函数,利用GA算法进行求解,研究结果表明使用遗传算法,模型在寻优过程中,种群的解能够很快收敛到最优解.Maddah和Ghasemi[16]采用神经网络研究了热媒特性对双管传热效率的影响,输入数据为热流体的温度、冷流体的温度、热流体的流速、冷流体流速、热媒流体的纳米特性,输出为传热效率.Wongwises和Chokeman[17]实验研究了风机盘管翅片间距和管排数对各种翅片厚度和管式热交换器的空气侧性能的影响.D’Antoni等[18]提出了一种用于瞬态仿真为目的的风机盘管数值模型,该模型使用模块化定义,适用于建模任何几何形状的风机盘管,用于评估其传热性能和控制策略的优化.Bruno,Anita等[19–20]开发了一个面向控制的风机盘管系统模型,采用盘管进风温度和湿度、空气速度、霜冻重量、盘管表面温度、传热流体的质量流量及其在盘管入口和出口的温度及环境温度作为输入,盘管出风温度和湿度作为输出参数,通过巩固物理建模、识别方法和制造商的目录数据来进行识别.凌飞[21]建立了一个可以应用于不同风机盘管,不同工况的换热模型,根据能量平衡和热传递原理,简化了换热模型,根据风机盘管结构参数及试验数据可以计算出盘管的换热系数,最终得到盘管的制冷量.
然而,上述文献大多使用白箱与黑箱建模,其中白箱建模文献占比50%,黑箱建模文献占比30%,在实际工程应用过程中,物理机理模型和数据驱动模型都表现出了各自的局限:物理机理模型大多基于实验室试验结果,需要物理参数难以在实际工程中获取,难以模拟实际动态工况下的风机盘管系统的物理特性,并且难以将模型中参数的不确定性传导至实际工况中.数据驱动模型的准确程度依赖于数据的质量,在数据不充分、不准确或不相关的情况下往往难以得到准确的预测结果,并且由于数据驱动模型需要拟合特定的历史数据,其可解释性可推广性也存在疑问.而灰箱建模能充分结合两类建模方法优势,避免单一方法缺陷,使二者扬长避短、互为补充,通过实验数据辨识制造商未能提供的相关参数,得到更精确的数学模型.风机盘管所采用的控制模型大部分都是单独考虑其水力模型或热力模型,并未考虑将风机盘管系统所涉及的水力和热力模型进行整合,且传统的风机盘管控制方式是通过对盘管的水阀通断控制及风机的3档调速控制满足用户的需求,目前电动水阀在空调箱中使用较多,在风机盘管中的应用也已经逐渐展开,且对于盘管水流量基本都是基于管网水力计算模型利用GA算法求解.针对上述问题,本文在考虑风机盘管电动水阀影响下,提出了混合热工和水力特性的风机盘管系统建模方法,建立适用于实际工程、面向优化控制并且能够反映风机盘管系统物理过程的数学模型,形成风机盘管热工水力模型,用以支撑根据建筑每个区域的热需求实现动态控制,满足实际工程的需要.本研究主要贡献在于:
1) 提出面向控制的风机盘管模型,将风机盘管的水力模型与热力学模型结合在一起,形成风机盘管热工水力模型,根据建筑区域的实际需要实现风机盘管的动态流量和风速控制;
2) 在水力学模型中考虑风机盘管电动水阀,将风机盘管加热/冷却管网拓扑等效为电气模型,基于基尔霍夫定律建立水力平衡方程,采用GA-PSO优化算法求解各盘管的水流量及对应的电动水阀开度;
3) 基于水力学模型可以得到风机盘管分支管道的水流量分布,在此基础上通过牛顿冷却定律建立风机盘管热力学模型,采用非线性最小二乘法辨识总传热系数,计算风机盘管的总功率.最后,通过某办公大楼实测数据验证了风机盘管系统模型的准确性.
2 风机盘管系统模型的建立
风机盘管机组的结构简单,主要由盘管和风机组成,多个风机盘管机组并联到一条供回水管道形成风机盘管系统,作为空调系统的末端装置,分散地装设在各个空调房间内,所需的冷热水通过空调机房集中制备,通过水管网供给风机盘管机组.风机盘管系统建模包括风机盘管机组传热与热交换的热力学模型和风机盘管供回水管网的水力模型,原理图如图1所示.
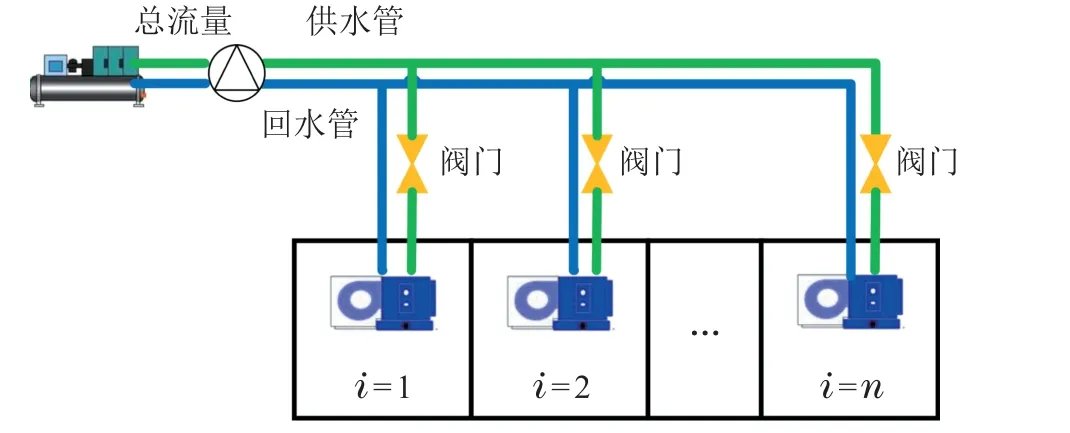
图1 风机盘管系统原理框图Fig.1 Schematic diagram of fan coil control system
2.1 水力学模型
风机盘管(fan coil unit,FCU)水力模型的优化目标通常为管网的最小压降,主要是对水力系统建模,把复杂水力系统模拟为类似的电气模型,利用GA-PSO算法求解得到满足负荷需求的各支路流量以及对应的电动水阀开度.
基于电气模型等效导出了风机盘管加热/冷却管网拓扑图,如图2所示.
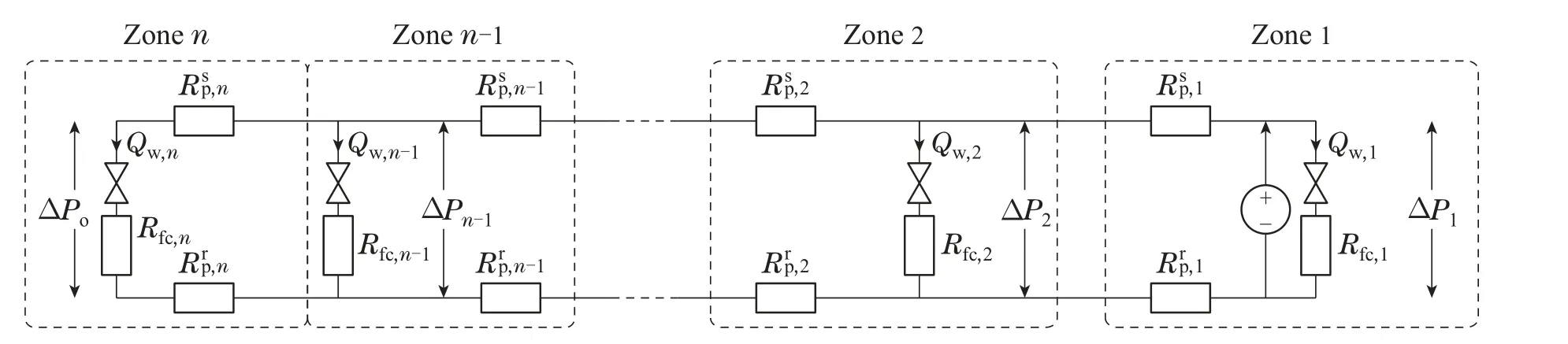
图2 风机盘管加热/冷却管网拓扑图Fig.2 Topology diagram of fan coil heating/cooling pipe network
对于等效电路的每个闭环,在知道水力阻力和质量流量的情况下,可以通过基尔霍夫电路定律表示FCU压降,如式(1)所示:
式中:∆Pj是第j个平行分支压降,包括通过FCU的压降和相关供回管道压降;∆Pj+1是第j+1个平行分支压降;∆Pj=∆Po是整个系统的整体压降;Qw,i是通过第i个FCU的水流量;是第j个FCU的给水阻力;是第j个FCU的回水阻力.
FCU水流量Qw、压降∆Pf和阻力R分别相当于电流、电压和电阻,其压降特性方程如式(2)所示:
电动水阀流量模型主要是根据管道的水流量以及阀门开度值得到阀门的阻抗值.电动水阀的流量特性是指电动水阀的相对流量与相对开度之间的函数关系式,如式(3)所示[22]:
式中:Q为当前通过电动水阀的流量;Qmax为电动水阀所能通过的最大流量值;L/Lmax为相对开度,即电动水阀的行程之比.
典型的理想流量特性包括直线流量特性、等百分比流量特性、快开流量特性和抛物线流量特性等4种类型,如图3所示.调节阀的应用场所: 快开调节阀适用于开关控制;线性调节阀适合于蒸汽盘管、三通阀旁通部分及旁通管路;等百分比特性调节阀门适合于加热器和风机盘管控制;抛物线调节阀具有截止、平衡、两通和三通功能.
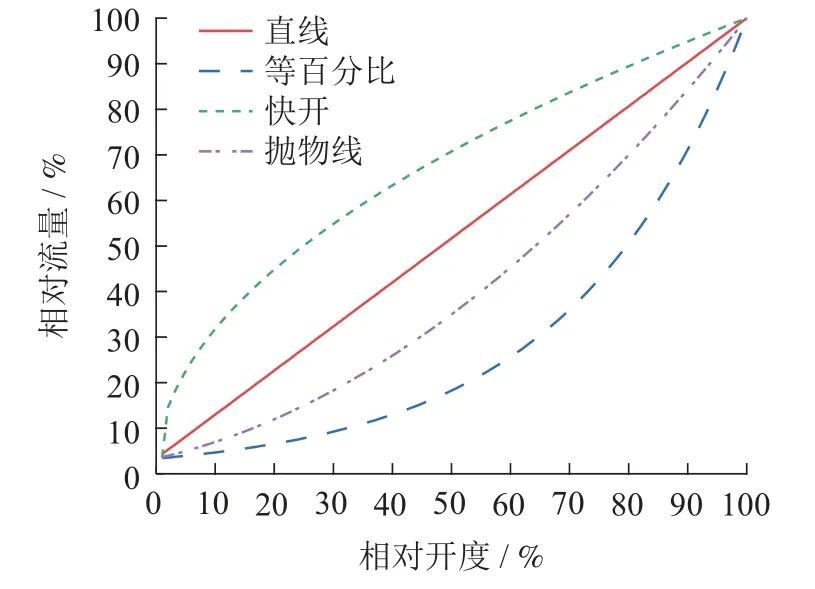
图3 调节阀的理想流量特性曲线Fig.3 Ideal flow characteristic curve of regulating valve
对于风机盘管,其本身流量与压降之间的关系为抛物线特性,但在实际的运行过程中,为了更好地调节温度,国内外普遍认为在供暖和空调换热器控制中,宜采用流量与阀门开度之间为等百分比特性的电动水阀,如式(4)所示[23]:
式中R=Q/Qmax为电动水阀的可调比或可调范围,即电动水阀最大流量与最小流量的比值,对于一般电动水阀来说,由于其最小可控流量为3.3%∼4%,故其可调比为25∼30,从安全角度考虑,本文可调比取30.
根据式(2)所示的FCU阻力特性和式(5)所示的阀门阻力特性,可得到阀门的阻抗系数与阀门开度之间的关系,如式(6)所示:
式中: ∆Ps为电动阀门两端压降,S为电动阀门的阻抗,S0为电动阀门全开时的阻抗系数,SL为电动阀门开度为L时的阻抗系数.
因此,FCU系统水力模型的目标函数和约束条件如式(7)所示:
式中:o是传感器测量通过FCU系统总的水流量;Qw,o是计算得到的FCU系统总流量;∆Po是通过管网的总压降.
2.2 热力学模型
基于水力学模型可以得到风机盘管分支管道的水流量分布,经过风机的三档转换对室内温度进一步进行调控,达到各个区域的需求温度.由牛顿冷却定律[24]可以计算风机盘管的总功率,如式(8)所示:
式中:F为风机盘管换热面积,根据风机盘管进行取值,单位m2;U为总传热系数,单位W/(m2· ◦C);∆Tm为对数平均传热温差.
考虑到FCU热力学模型主要涉及传热系数的求取,因此对于给定的FCU换热器,总传热系数U主要由内外表面的换热系数决定,在实际工作中往往把风机盘管的传热系数整理成以下的经验式,如式(9)所示[21]:
式中:A,B,r,n为模型的待定常数,x为FCU的风量.
在风机盘管的实际运行中,空气–水的流动方式为逆流方式,其对数平均传热温差的计算如式(10)所示:
3 模型求解
3.1 水力学模型求解
FCU建立的水力模型属于非线性优化问题,采用优化算法进行求解.GA算法和PSO算法都属于智能算法,主要是解决全局优化问题,在搜索最优解时,有各自的优点和缺点,可以结合两种算法的优点来改进各自算法在寻优过程中的缺点.GA算法具有快速性、并行性和较强的全局搜索能力,但不能很好利用反馈信息,寻优过程收敛速度较慢;PSO算法有着较好的搜索精确度和速度,但容易陷入局部最优.因此,将两种算法混合,将GA的交叉和变异操作引入PSO算法中,从而提高收敛速度和求解精度.
具体的优化步骤如下:
步骤1种群初始化,设定种群大小popsize=10、维度N、粒子上下界(水流量取值范围为[0,5]及阀门开度取值范围为[0.3,1]),速度取值上下界[0,1],迭代次数maxgen=50,学习因子c1,c2和交叉、变异算子,初始化种群的速度和位置;
步骤2输入约束条件,计算初始种群的管网总压降值,将初始化粒子(支路流量和阀门开度)代入FCU水力优化模型,求解压降最小时对应的水流量和阀门开度值,记录种群的个体最优值gbest及全局最优值zbest;
步骤3更新粒子(支路流量和阀门开度)的速度和位置,产生新种群,其速度和位置通过公式(12)和(13)来更新,
步骤4按照给定的交叉概率pc,将筛选后的粒子(支路流量和阀门开度)进行交叉操作,随机选出两个粒子进行交叉,直到所有粒子完成交叉操作;
步骤5对杂交后的新粒子(支路流量和阀门开度)重新进行计算管网总压降值并排序,更新个体最优值及全局最优值;
步骤6按照给定的变异概率pm,将筛选后的粒子(支路流量和阀门开度)进行变异操作,随机选出两个粒子进行交叉,直到所有粒子完成变异操作;
步骤7对变异后的新粒子(支路流量和阀门开度)重新进行计算管网总压降值并排序,更新个体最优值及全局最优值;
步骤8判断是否满足终止条件,若满足,立即停止迭代运算并输出压降最小时对应的水流量和阀门开度值结束,否则返回步骤3.
GA-PSO算法流程图如图4所示.

图4 GA-PSO算法流程图Fig.4 GA-PSO algorithm flow char
3.2 热力学模型求解
对于特定的风机盘管,总传热系数U可通过盘管的风量和水的质量流量来确定.由于未知参数较多,因此无法直接求解,但可以通过非线性最小二乘法来确定模型的未知参数,最终得到总传热系数的表达式[25].如式(14)所示:
非线性最小二乘法的实现方法众多,主要方法有搜索算法和迭代算法两类[26].本文采用基于非线性最小二乘的Levenberg-Marquardt(LM)迭代算法进行求解,该算法实现简单、精度高、迭代次数少,可以得到良好的辨识效果.LM算法结合了两种最优化算法: 梯度下降法和高斯–牛顿法.
高斯–牛顿法的迭代方程形式为
LM算法在高斯–牛顿法的基础上引入了阻尼因子调节算法特性,如式(16)所示.随着阻尼系数µ的增大,计算结果偏离最优解的程度也相应提升;相反,随着阻尼系数µ的减小,计算结果趋近于最优解.
LM算法操作步骤如下:
步骤1初始化参数,设置控制精度ε=10-6,阻尼因子µ0=10-3;
步骤3求出雅克比矩阵J(k);
步骤4误差函数e(k)<µ,U(k)为最优值,转到步骤6;否则,将U(k+1)作为新的处置向量计算误差函数,且满足e(k+1) 步骤5如果e(k+1) 步骤6完成并停止. 在本文的研究中选取西安建科大厦进行验证,以其中一层办公区域,走廊两边为办公室区域,共10间独立办公室,该区域面积350 m2,高3 m,外围护两面是混凝土墙,厚度为35 mm,顶部是混凝土板,厚度为30 mm.每个房间设定为一个区域,由中央空调系统统一供冷/供热.本案例中,每个区域分别设置1个风机盘管,其中包括3 个FP-102 型FCU,5 个FP-136 型FCU和2个FP-170型FCU,每个风机盘管的进水管道处安装有可调比为30的相同等百分比特性的电动水阀,并在每个楼层房间的风机盘管供水管道上安装热量计(UH50-A50-00),采样时间间隔为1 min,通过热量计测量供回水温度、送风温度、水流量和热功率.管道长度定义为两个连续FCUs之间水平段长度或FCU与热量计之间的长度.根据制造商所给数据得到FCU的型号以及西安建科大厦的10个房间的具体数据,如表1所示. 表1 FCU系统房间相关参数Table 1 Flow distribution of each branch pipe of FCU hydraulic system 由于FCU型号的不同,导致其性能曲线也并不相同;在此,利用系统的实际运行数据对各风机盘管性能参数进行辨识,以获得更加准确的模型,风机盘管的性能参数如表2所示.以FP-102为例,得到FCU的压降特性曲线图如图5所示,Q示通过风机盘管的水流量,∆P表示通过风机盘管的压降,根据最小二乘法拟合得到FP-102的压降公式如式(18)所示. 表2 FCU性能参数表Table 2 Performance parameters of FCU 图5 FP-102的压降特性曲线图Fig.5 FP-102 pressure drop characteristic curve 为了保证办公区域的热舒适性和提升工作品质,风机盘管系统根据办公人员的工作及作息时间进行分工况运行,热量计测量的实际运行结果具体如表3所示. 表3 FCU系统工况运行参数表Table 3 FCU system operating parameters table 热量计(UH50-A50-00)安装在每个楼层房间的风机盘管供水管道上.热量计以1 min的时间分辨率测量供回水的温度、温差、水流量和热功率.以测量第8个房间的回水温度和水流量为例,验证其准确性,温度传感器和流量传感器的最大测量误差均为±0.2%,图6为FCU回水管上得到热量计温度测试误差图,图7为FCU供水管上得到热量计水流量测试误差图. 图6 热量计温度测试误差图Fig.6 Error chart of calorimeter temperature test 图7 热量计水流量测试误差图Fig.7 Error chart of calorimeter water flow test 图6中直线代表标定过的温度传感器测量值与热量计测量值完全相同,热量计测量的供冷和供热回水温度基本分布在校准曲线上,同时计算热量计测量温度值的误差,均方根误差(root mean squared error,RMSE)为0.82,平均绝对百分比误差(mean absolute percent error,MAPE)为0.16. 图7中直线代表标定过的流量计测量值与热量计测量值完全相同,热量计测量的水流量基本分布在校准曲线上,同时计算热量计测量水流量值的误差,均方根误差RMSE 为0.53,平均绝对百分比误差MAPE为0.11.因此,热量计对风机盘管系统建模验证的可信度较高. 4.3.1 水力学模型 为了验证GA-PSO算法的可行性,所建立的模型在西安建科大厦的10间办公区域内进行验证,根据逐时热负荷预测结果,通过Q=c×ρv×∆t即可得到满足该办公区域内各房间热负荷需求的所需水流量Q.采集了在2020.05.01–2021.03.15的9: 00–22: 00办公区域风机盘管系统不同工况下的实际运行数据,经过对总流量需求的计算,可知2020.05.20(低温天气)和2020.07.30(高温天气)分别为表3中夏季供冷的工况1和工况3,2021.03.10(高温天气)和2020.12.23(低温天气)分别为表3中冬季供热的工况2和工况4,在对风机盘管系统的管网完成静态水力平衡的基础上,使用GA-PSO算法对其进行优化求解.为避免实验偶然性,进行了50次独立优化实验,将最终优化的实验结果与热量计测量的实际运行结果对比如表4所示. 表4 实际运行结果与算法优化运行结果对比Table 4 Comparison of actual operation conditions and algorithm optimization operation results 从表4中可以看出,该风机盘管系统运行控制策略在未优化前虽然可以维持管网水力平衡,但与优化后的结果相比,支路流量结果与实际值都很相近,其相对误差均不超过1%,且与优化后的结果相比,实际运行中的支路阀门开度偏小,这导致整个管网的阻抗增大,从而增加了系统的运行能耗;而经过算法优化后,各支路阀门的开度相对于优化前显著增大,并且在此条件下各支路流量均能达到流量需求值,从而减小了管网系统的阻抗,使得系统供回水压差降低,在源头上降低了整体的能耗. 为了进一步验证GA-PSO算法的性能,在不同工况下对所提出的GA-PSO算法的性能进行实验分析,并将优化结果与GA,PSO算法进行对比,同样为了避免实验偶然性,对每种工况迭代50次,得到的优化结果如表5–表6所示.4种工况下GA-PSO优化的风机盘管支路流量与实际相对误差如图8所示,在工况1下各算法所得风机盘管支路流量相对误差对比如图9所示. 表5 算法优化后的支路阀门开度对比Table 5 Comparison of branch valve opening after algorithm optimization 表6 算法优化后的支路流量对比Table 6 Comparison of branch flow after algorithm optimization 图8 GA-PSO算法所得风机盘管支路流量相对误差图Fig.8 The relative error diagram of the fan coil branch flow rate obtained by the GA-PSO algorithm 图9 工况1各算法所得风机盘管支路流量相对误差图Fig.9 The relative error of the fan coil branch flow rate obtained by each algorithm under working condition 1 从表5可以看出,没有对阀门开度进行优化时,实际阀开度在3种工况下虽然能够达到动态水力平衡,但是所有的阀门开度相比优化后的结果更小,得到的总压降更大,这将大大增加整个管网系统的阻抗,造成能耗的浪费.而经过GA,PSO和GA-PSO算法优化后,各支路的调节阀开度总比实际阀开度大,从而使得优化后的供回水压差减小,且GA-PSO的阀门优化求解算法精度比GA算法和PSO算法均要高,在相同的工况下能够获得更优的解和更小的管网系统总阻抗,能有效地减少风机盘管的运行功率.在表6的3种工况优化策略的结果中可以看出,GA,PSO 和GAPSO算法所得的运行结果可以发现支路流量结果与实际值都很相近,且GA-PSO算法得到的结果更加接近需求值,且4种工况下GA-PSO算法优化后风机盘管支路流量的RMSE分别为0.0087,0.0054,0.0038,0.0049;MAPE分别为0.062,0.052,0.034,0.044,从误差分析指标可以得出水力系统所求的流量分配值与实际测量值基本吻合,验证了模型的准确性. 结合表6和图8–9可以看出,GA和PSO算法所得到的运行结果也较好的控制了风机盘管的流量,但是其精度略低于GA-PSO算法,GA-PSO算法得到的结果更加接近需求值,其相对误差最大为0.87%,最小可达到0.18%,可以较好地分配支路流量,在管网动态水力平衡的前提下达到了供需平衡;而GA优化后的支路流量虽然也能基本满足需求,但其精度低,相对误差最大达到了2.5%,PSO优化后所得到的运行策略也能较好的控制支路流量,但其相对误差最大也达到了2.7%,GA 和PSO 算法的最大相对误差已经大于GAPSO 算法的最大相对误差.因此,GA-PSO 算法能够很好地求解风机盘管支路流量.GA-PSO算法不但在寻优求解方面精度高,而且具有良好的收敛性,为了更好地分析其在算法收敛性方面的性能优势,本文将GA-PSO 算法与GA 算法、PSO算法的收敛性在各工况下进行了进一步的比较.3种算法所得结果与流量需求量的残差迭代变化曲线如图10所示. 图10 原始残差迭代收敛图Fig.10 Convergence graph of original residual iteration 由图10可以看出,GA算法分别在4种工况下在第20–25代达到收敛,PSO算法分别在4种工况下在第15–20代达到收敛,而GA-PSO算法在10代左右均能达到稳定状态,这是因为GA算法寻优过程收敛速度较慢,PSO算法容易陷入局部最优,而GA-PSO算法寻优求解精度高,具有良好的收敛性,因此GA-PSO算法能够进一步加快收敛速度、缩短计算时间;同时,相较于GA算法、PSO算法,GA-PSO算法获得的收敛误差迭代曲线更为平坦.因此,GA-PSO算法具有很好的稳定性和收敛性. 4.3.2 热力学模型 根据制造商数据得到风机盘管换热器的有效换热面积为6.653 m2.基于水力学模型求解的水流量及格力制造商所给数据,通过建立的热力学模型辨识出型号为FP-102的风机盘管待定模型参数A,B,r,n.利用最小二乘法求取风机盘管的总传热系数,为了验证总传热系数表达式的准确性,用200组数据进行模型拟合,50组数据进行仿真计算,得到待定模型参数如表7所示,供冷和供热季节取值是相同的,且不随风机速度的变化而改变. 表7 传热模型的待定系数表Table 7 Table of undetermined coefficients of the heat transfer model 夏季供冷时间一般在6–9月,6–7月左右室外温度较低,系统处于低工况运行状态;8–9月室外温度较高,系统处于高工况运行状态.为了验证模型的真实性与实用性,选取第8个房间对模型验证,在夏季低、中、高工况分别取一天8: 00-22: 00 测量,采样时间间隔为30 min.夏季低、中、高工况下供回水温度、送风温度以及室外温度情况,风机盘管转速及热功率对比情况分别如图11–13所示. 图11 夏季低工况温度及功率对比图Fig.11 Comparison of temperature and power under low operating conditions in summer 图12 夏季中工况温度及功率对比图Fig.12 Comparison of temperature and power under middle operating conditions in summer 由图11–13可知,夏季处于低工况时,室外温度最高为30◦C,风机转速基本处于低档和中档,风机盘管的热功率最大为2.9 kW;处于中工况时,室外温度最高为32◦C,风机盘管的热功率最大为3.5 kW;处于高工况时,室外温度最高为35◦C,风机转速基本处于中档和高档,风机盘管的热功率最大为4.5 kW,故风机盘管消耗的热功率比中、低工况下的热功率大.当处于高工况下,早上九点时风机开度处于高速状态来调节室温;中午十二点至两点休息时间,盘管开度降低,风机盘管消耗的热功率降低.因此,风机开度越大,消耗的功率越多;且夏季低、中、高工况下风机盘管消耗的热功率RMSE分别为0.152,0.206,0.168;MAPE分别为0.167,0.311,0.197,从误差分析指标可得出热力学模型所求的热功率与量热计测量值基本吻合,这说明热力学模型获得的区域热功率结果比较精确. 由图11–图13可知,夏季处于低工况时,室外温度最高为30◦C,风机转速基本处于低档和中档,风机盘管的热功率最大为2.9 kW;处于中工况时,室外温度最高为32◦C,风机盘管的热功率最大为3.5 kW;处于高工况时,室外温度最高为35◦C,风机转速基本处于中档和高档,风机盘管的热功率最大为4.5 kW,故风机盘管消耗的热功率比中、低工况下的热功率大.当处于高工况下,早上九点时风机开度处于高速状态来调节室温;中午十二点至两点休息时间,盘管开度降低,风机盘管消耗的热功率降低.因此风机开度越大,消耗的功率越多;且夏季低、中、高工况下风机盘管消耗的热功率RMSE分别为0.152,0.206,0.168;MAPE分别为0.167,0.311,0.197,从误差分析指标可得出热力学模型所求的热功率与量热计测量值基本吻合,这说明热力学模型获得的区域热功率结果比较精确. 图13 夏季高工况温度及功率对比图Fig.13 Comparison of temperature and power under high operating conditions in summer 冬季供热的时间是从11月中旬维持到3月中旬,2–3月左右室外温度较低,系统处于低工况运行状态;12–1月室外温度较高,处于高工况运行状态.当系统处于高工况运行状态,要满足高负荷的需求运作;温度稍有上升时,低工况的状态便能满足室内温度舒适性.选取第9个房间对模型验证,在冬季低、中、高工况分别取一天8: 00–22: 00测量,采样时间间隔为1 h.冬季低、中、高工况下供回水温度、送风温度以及室外温度情况,风机盘管转速及热功率对比情况分别如图14–16所示. 图14 冬季低工况温度及功率对比图Fig.14 Comparison of temperature and power under low operating conditions in winter 图15 冬季中工况温度及功率对比图Fig.15 Comparison of temperature and power under middle operating conditions in winter 图16 冬季高工况温度及功率对比图Fig.16 Comparison of temperature and power under high operating conditions in winter 由图14–16可以看出,冬季处于高工况时,受室外环境中冷空气影响供应温度产生一定的波动,中午温度较早晚高些,风机开度根据温度变化改变;早上温度低,调大风机开度以保证室内热舒适,中午可随室温需求适当降低开度,在保证人体温暖舒适的前提下适当节能.高工况时的风机转速基本处于中档和高档,故风机盘管消耗的热功率比中、低工况下的热功率大,且冬季早晚温差较大,最冷温度可达到–6◦C,所以需要消耗更多的功率来达到设定的温度.实验得出的冬季低、中、高3种工况下风机盘管消耗的热功率RMSE分别为0.167,0.154,0.129;MAPE分别为0.195,0.307,0.242,从误差分析指标可以得出热力学模型所求的热功率与量热计测量值基本保持一致,验证了热力学模型的准确性.因此热力学模型适合各种工况条件下的热功率计算. 本文基于风机盘管控制系统模型,提出了在水力模型引入电动阀门控制水流量,并采用基尔霍夫定律等效电路模型精确反映出了风机盘管的水流特性,在满足建筑办公区域的负荷需求下使管网总压降最小,减少能源消耗,结合GA 和PSO 算法的优点引入GAPSO算法进行求解水力模型的水流量及对应的电动阀门开度,其相对误差不超过1%,达到了支路流量按需分配的要求,且验证了GA-PSO算法具有鲁棒性好、稳定性强、准确性高的特点;采用牛顿冷却定律建立热力学模型,在各种工况下的模型误差都低于4%,验证了风机盘管的传热过程.本文所提出的风机盘管控制系统模型仅在每层楼供水管道安装传感器,减少了传感器的数量并节约了成本,而且通过风机转速和电动阀门开度直接控制每个办公区域的热能输入,保持室内的舒适性,能更好地实现精细化控制.4 工程案例
4.1 案例描述
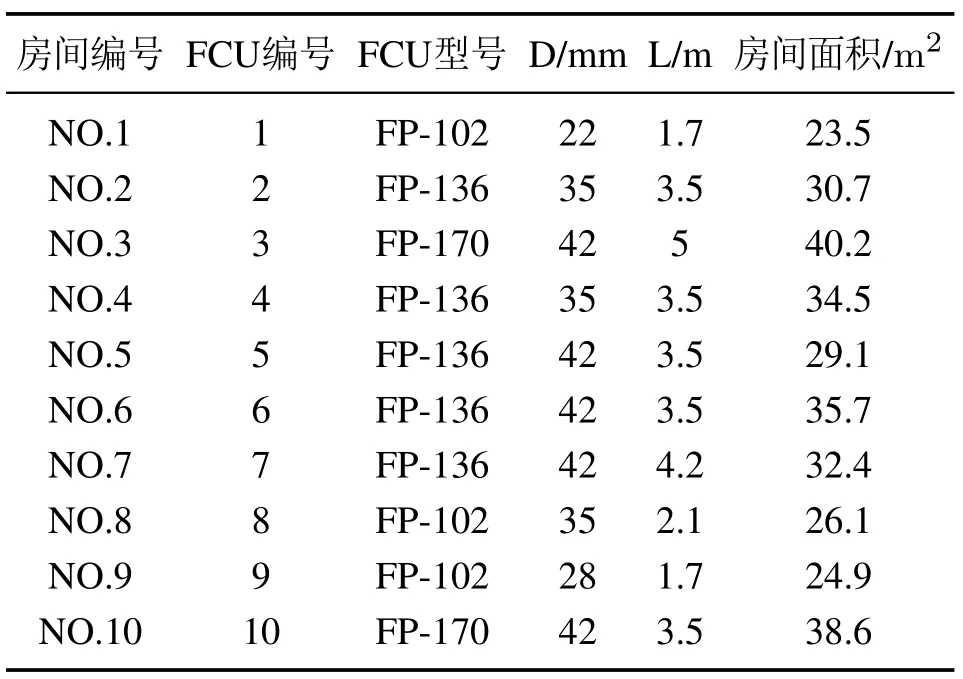
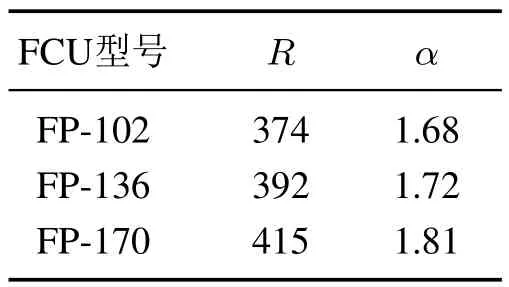
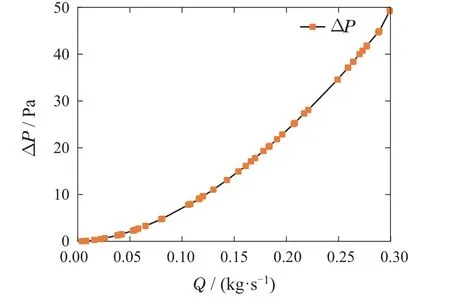
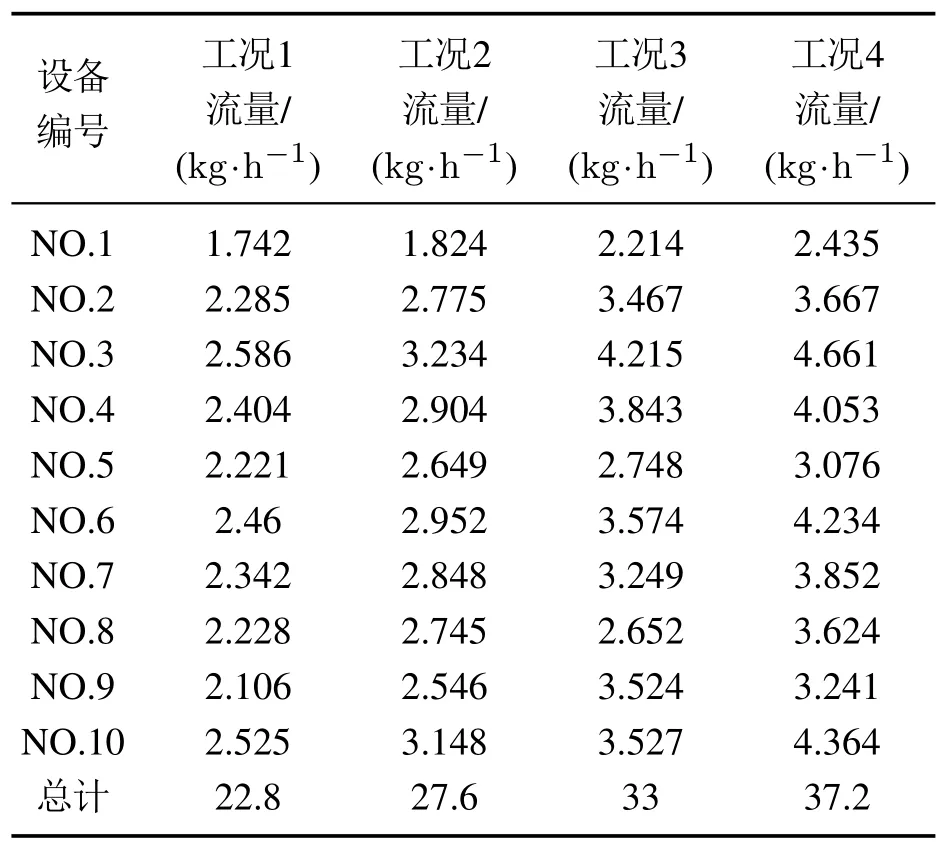
4.2 热量计校准
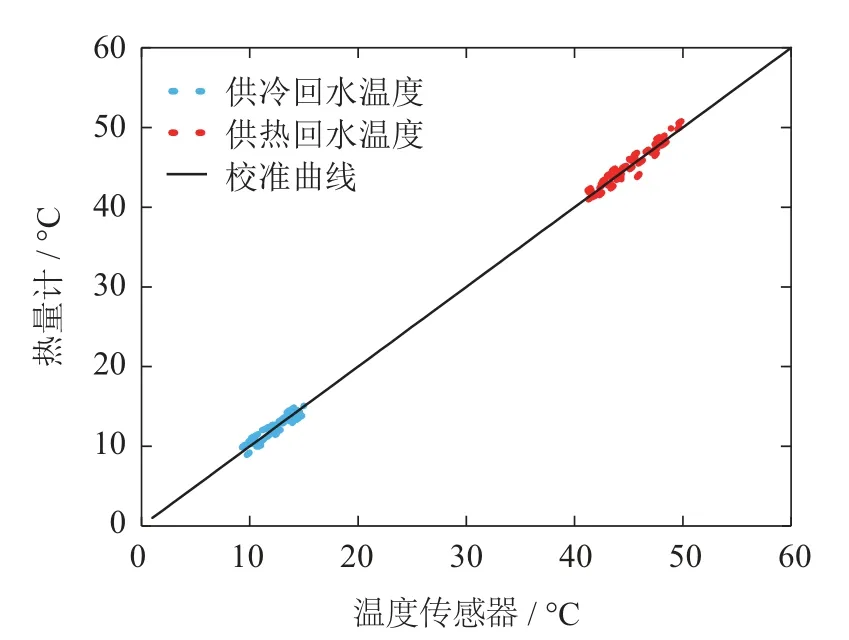
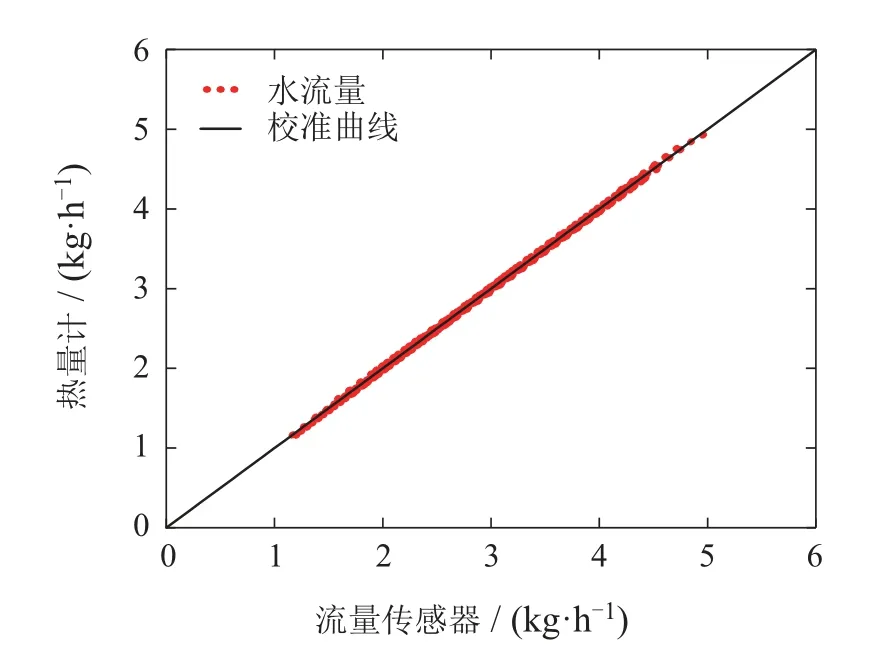
4.3 结果分析
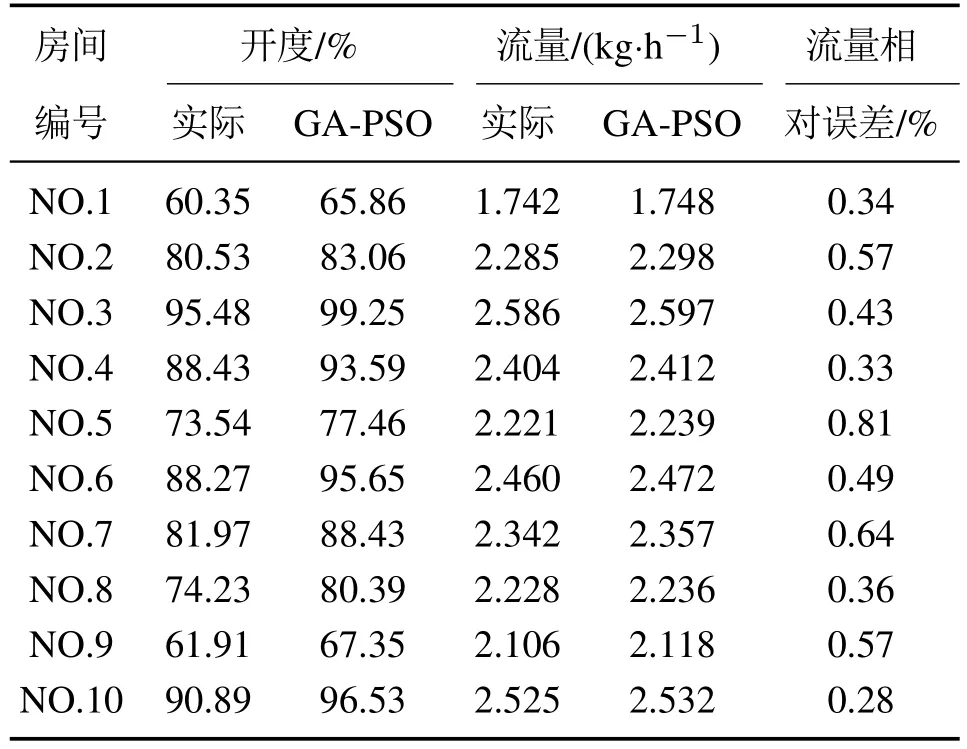



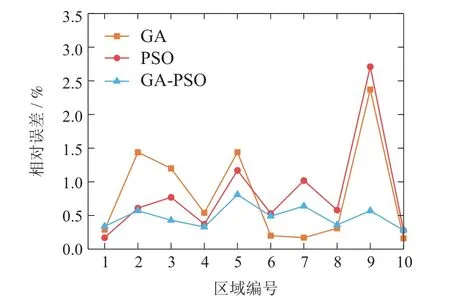


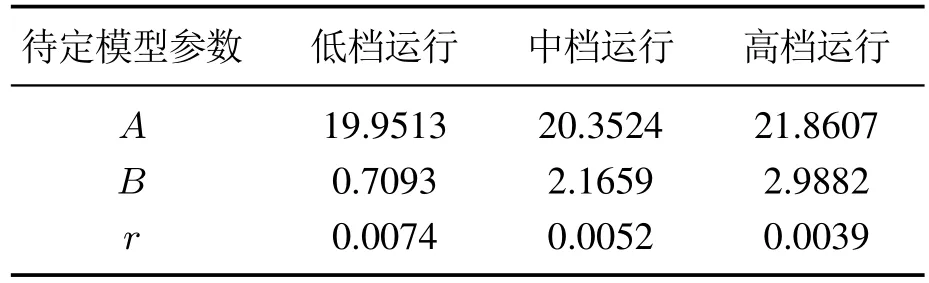

5 结论

