考虑无线充电的无人机路径在线规划
张 涛 ,刘 威 ,王 锐 ,李凯文 ,徐万里
(1.国防科技大学系统工程学院,湖南 长沙 410073;2.军事科学院系统工程研究院,北京 100080)
1 引言
近年来,无人机应用领域不断拓展,在物流配送[1]、灾害救援[2]、军事侦察打击[3]、设备巡检[4]、无线通信中继[5]等领域得到了广泛应用.近日俄罗斯与乌克兰的战争中,“里尔–3”、“海雕–10”等无人机大放异彩,成功完成了监视、干扰、打击等战术目的.随着无人机应用的愈发普及,无人机的续航能力瓶颈也愈发凸显[6],当前无人机续航大多为几十分钟,电量耗尽需要人员进行降落、回收、再起飞,但是在灾害救援、军事等应用场景下,通常由于地理工况复杂、人员人身安全受威胁,不便进行无人机的频繁降落,这极大制约了无人机的使用.
无线能量传输技术最初由Nikola Tesla在20世纪初研究[6],随着近年来电磁感应、磁耦合谐振等远程无线供能技术的不断突破和发展,无线能量传输技术愈发成熟[7].采用无线充电技术,无人机只需要进入有效距离即可实现能量自动补给,而不需要进行降落,从而有效提高其续航能力和工作范围,2021年12月,美国国防高级研究计划局(DARPA)资助Electric Sky公司进行无人机无线能量传输技术研究,以拓展无人机在军事、救援等极端环境下的应用.
该背景下,本文研究考虑无线充电的无人机路径规划方法,通过无线充电技术实现无人机任务全过程的无人化、自动化,降低极端任务环境下的人工成本和安全风险.同时,在军事和灾害救援等领域,系统响应速度至关重要,但传统优化方法的计算时间随着问题维度呈指数增长,很难进行实时规划和快速响应,亟需研究高效的在线优化方法.随着近年来人工智能技术的蓬勃发展,深度学习技术使得复杂优化问题的实时在线优化成为了可能,谷歌大脑在2016年提出了一种指针网络模型[8]来解决传统组合优化问题,无需迭代搜索,神经网络可以直接输出问题的解,实现了旅行商等优化问题的快速求解;文献[9]提出使用强化学习方法来训练指针网络模型,相对于监督式训练方法,强化学习方法无需构建数据集,并且模型具有更强的探索性能;文献[10–13]将该方法拓展至车辆路径优化、定向以及多目标旅行商等问题,实现了优化问题的在线求解.但是当前的该类方法大多针对经典路径优化问题,研究的对象相对简单,在复杂实际应用问题上的研究较少.
目前研究无线充电场景下无人机路径规划问题的文献较少,多为传感器网络中无人机位置的部署,文献[14–15]将无人机作为无线充电的供能中继节点,对10节点规模的无线通信网络中无人机的位置进行优化;文献[16]将无人机作为无线充电发射端与接收端之间的中继端,对中继节点各时刻的位置进行优化;文献[17]使用无人机为无线传感器网络中的节点进行无线充电,采用遗传算法对50个节点的小规模传感器网络进行了研究.当前文献大多采用进化算法等传统优化方法对无人机的位置、路径进行优化,研究问题的规模较小,一旦问题规模增大,传统优化算法面临着求解时间指数增加的问题,无法实现实时在线规划,很难应用于军事、灾害救援等对于优化引擎求解速度要求高的领域.
考虑传统算法在实时在线优化能力上的瓶颈以及实际应用领域对无人机路径规划高响应速度的要求,本文提出一种基于深度强化学习的无人机路径优化方法,对无线充电场景下的无人机任务路径进行在线优化.具体地,考虑一种受限时间下无人机访问任务节点的典型场景,基于各任务节点的重要度对路线进行规划.分别构建无人机功耗模型、无线能量传输模型、深度神经网络模型,采用深度强化学习算法对模型参数进行优化,基于训练好的模型实现无人机路径的实时在线输出,从而极大提高无人机路径寻优的求解速度,实现考虑无线充电的无人机路径优化问题精准和快速的求解.
2 系统建模
2.1 问题描述
本文对基于无线充电的无人机路径规划问题进行研究.具体地,采用基于无线充电的无人机对目标区域内的多个任务点实施侦查、打击等任务,每个任务点具有不同的任务优先级(重要度)ri,无人机以满电量状态从基站出发,前往各个任务点执行任务并返回基站.对无人机的任务路径π进行规划,由于任务时间限制,需要在时间限制T内完成尽可能多的任务,由于每个任务点具有不同的重要度,因此规划目标是最大化无人机访问的任务点的总重要度.
由于电池容量限制,一旦无人机电量(state of charge,SoC)降低到给定水平(本文为20%),需要进行无线充电,在靠近基站一定距离即可开始进行无线充电,如果到达基站上空时仍未充满,则悬停进行充电,随后离开基站继续执行任务.通过该种方式进行供能,能够实现无人机任务执行的全流程无人化、自动化,并克服战场、灾害等复杂工况下无人机降落、回收困难、人力成本大、人身安全风险高等问题.在该问题场景中,本文假设任务点和基站分布在同一平面中,由XY坐标表示,无人机在固定高度H以速度V进行匀速飞行,在该条件下,分别构建无人机功耗模型、无线充电模型以及系统优化模型.
2.2 无人机功耗模型
首先对无人机飞行时的功耗模型进行构建,本文采用四旋翼无人机作为研究对象,无人机以速度V飞行时的功耗模型[15]构建如下:
其中:ρ,Ω,R,W分别是空气密度、叶片角速度、旋翼半径和无人机重量;v0表示旋翼平均诱导速度,Utip是旋翼叶片的叶尖速度,分别计算为[15]
当无人机悬停时速度V=0,其功耗为P(0)=P0+Pi,当无人机以速度V飞行时功耗为P(V).因此,旋翼无人机飞行和悬停所需的能量可以计算为EV=P(V)Tflying和Ehover=P(0)Thover.
2.3 无线充电建模
本文考虑的无人机无线充电分为两个阶段: 1)无人机在飞往基站的过程中,当与基站的水平距离达到阈值xstart时,基站开始对无人机进行无线充电,该阈值距离由无人机能量采集器的激活能量所决定;2)无人机在抵达基站顶部后,如果电池未充满,则悬浮充电直至充满.
假设无人机和基站之间无障碍物遮挡,则无人机和基站之间建立了一条视线传输链路(line of sight,LoS)链路.可采用自由空间路径损耗模型计算链路的无线能量传输损耗[15],即
其中:d是无人机与基站之间的距离,f是载波频率.
同时,考虑射频直流(radio frequency to direct current,RF-DC)的转换损耗,本文采用转换效率固定的线性转换损耗作为损耗模型,即
其中:η是转换效率,PRF是能量收集器的输入射频功率,PDC是电池的转换后直流功率.
综上,无人机从基站实际接收到的无线充电功率可计算为
其中:Pt是基站的发射功率,单位是dBW;Gt是基站发射天线的增益,单位是dBi;Guav是无人机的接收天线增益,单位是dBi;PL(d)为基站与无人机之间无线信道的传输损耗,单位为dB.式(7)展开为
由上式可知,充电功率随距离d变化,分别对无人机的悬停充电和移动充电建模如下.
2.3.1 悬停充电模型
无人机悬停在H高度时,充电功率恒定,即
因此在悬浮时间Thover,无人机接收到的能量为
无人机在悬停时消耗的能量计算为
假设无人机飞行至基站顶部时,仍需要充电的电量为Er,则悬停时间可计算为
2.3.2 移动充电模型
假设xbs为基站的位置,当无人机飞行至位置xstart时,基站开始为无人机充电,xstart+V t-xbs为基站和无人机之间能够进行充电的最远水平距离,否则,能量空间传输损耗过多,无法达到能量采集器的激发阈值.
假设该移动充电阶段的开始时间为t=0,在时间t,无人机与基站之间的距离为
则t时刻的充电功率为
其中Ω=Pt+Gt+Guav-20 lg(f)+147.55.
无人机从xstart飞到基站顶部所花费的时间计算为=(xbs-xstart)/V,则无人机在此充电阶段接收的总能量计算为[15]
因此,式(12)中,无人机到达基站顶部时仍然需要充电的电量Er计算为Er=Efull-Es-Efly,其中Es为无人机到达xstart时的剩余能量,据此可以计算得到无人机的悬停时间Thover.
2.4 优化模型
根据上述模型可以对该优化问题进行建模.令dij为节点i到节点j的距离,索引为0的节点为基站,假设无人机返回基站进行充电的次数为K次,即解由K个哈密顿回路组成,令xijk为决策变量,xijk=1代表第k个哈密顿回路存在从i到j的弧,每个任务节点的重要度为ri,优化目标为在时间限制T内访问的节点的总重要度最大,该优化问题建模为
3 深度神经网络模型
本文设计了一种基于动态上下文向量的的深度神经网络模型解决该路径优化问题,通过神经网络模型,将任务点地理位置的输入序列映射为无人机访问路径的输出序列,该过程可以类比为机器翻译,即单词序列映射,因此可借鉴广泛应用的Seq2Seq模型求解该问题.模型由编码器和解码器构成: 编码器采用Transformer模型[12,18]的多头注意力机制,用来提取任务节点的多维特征表示hi;解码器由循环神经网络和基于动态上下文向量的注意力机制组成,以自回归的方式构造解,该过程表示为
其中:s为问题输入,π为无人机的任务路径,在构造解的每一步t,模型根据无人机已访问过的节点π1∼t-1和问题的特征s输出选择任务节点πt的概率,每一步根据各节点选择的概率pθ(π|s)即可构造解.
pθ(π|s)由基于编码器和解码器的深度神经网络模型计算得到,其结构如图1所示.
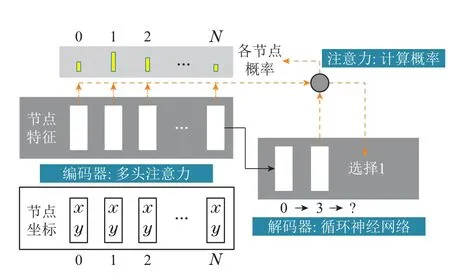
图1 深度神经网络模型结构Fig.1 Structure of the deep neural network
3.1 编码器
给定任务节点的二维坐标序列x,编码器将其转换为dh维度的节点特征向量hi,本文采用的多头注意力机制(multi-head attention,MHA)[12]来计算每个节点i的特征向量hi.
自注意力(self-attention)是MHA的基本组成部分,它计算每个节点对输入序列中所有其他节点的注意力值,使得每个节点的特征向量不仅存储了自己的信息,还存储了与其他节点的关系的信息,因此能够获得节点更加丰富的特征.
首先,采用参数为Wx和bx的全连接神经网络,将二维坐标序列x映射为dh维的初始节点特征h(0),即
第2步,计算每个节点的query,key和value向量,它们都是每个节点的初始特征h(0)的线性投影,计算为
其中WQ,WK,WV为不同的可训练参数.对于节点i,其注意力值由其query“查询”和所有节点的key-value“键值对”计算得到,即如果节点i的query“查询”和节点j的key“键”更加匹配,则赋予节点j的value“值”更大的权重.假设输入序列中有N个节点,对于节点i,它的注意力值是N个values的加权和,其中权重是通过节点i的query与N个节点的keys计算得到的,计算为qiKT.因此节点i 的注意力值计算为qiKTV.通常采用矩阵乘法进行计算加速
多头注意力将h(0)分割成M个子向量,进行M次自注意力计算,从而得到M个维度为dh/M的特征向量,尔后将M个向量进行拼接,进行线性投影到最终的dh维特征向量h(N),多头注意力机制使得节点获得更加丰富的特征表示.
编码器的神经网络结构如图2所示,由N个顺序相连的注意力层构成,每个注意力层由上述的多头注意力机制和全连接神经网络串联而成,通过多次注意力计算过程,可以计算得到具有丰富信息的节点特征表示h(N).
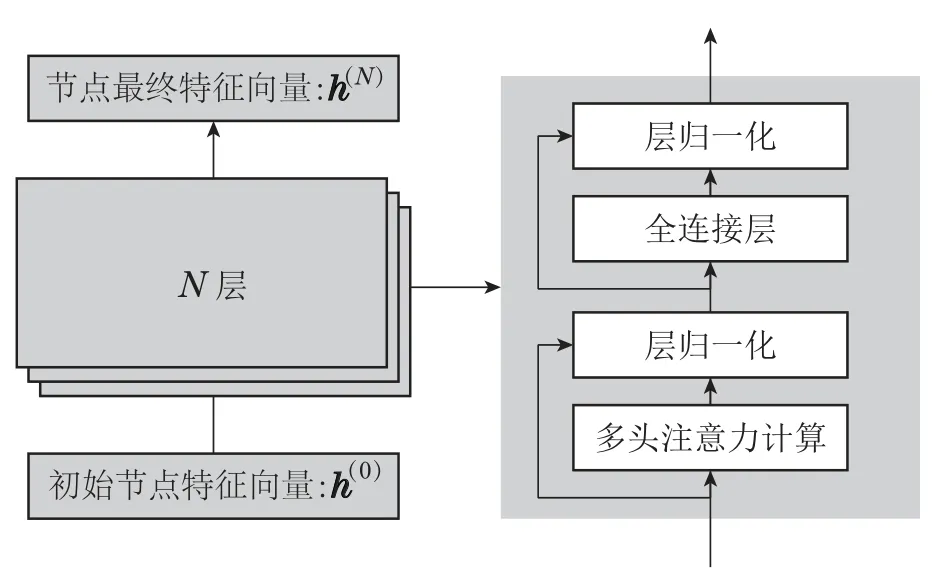
图2 神经网络模型编码器结构Fig.2 Encoder structure of the neural network model
3.2 解码器
解码器采用自回归的方式逐步构造解.在第t步解码过程中,通过节点的特征向量h(N)和当前的上下文向量(Context)计算选择各个节点的概率.上下文向量表示问题的当前状态,本文根据无人机的荷电状态信息和模型约束关系,设计了一种动态更新的上下文向量,使得模型能够更加有效地理解问题当前的状态,该上下文向量由基于循环神经网络表示的无人机已访问路径和无人机的当前的荷电状态SoC构成.
循环神经网络可以有效处理序列信息,本文采用门控循环单元(gated recurrent unit,GRU)循环神经网络对无人机已访问路径进行编码,首先,计算所有节点特征向量的平均值作为GRU 的初始隐层向量,即D0=.采用可训练参数v1作为第1步解码t=1时GRU的初始输入.在后续解码步t>1,GRU的输入是上一步所选择的节点πt-1的特征向量,GRU在第t步输出的隐层向量Dt存储了已访问节点的序列信息,代表解的当前状态.
无人机每次离开基站时,其SOC初始化为SOCt=1,访问节点时更新如下:
其中:πt=0的节点代表基站,dis(∗,∗)代表两个节点之间的距离.因此在第t步解码过程中,上下文向量计算为dt=[DtSOCt].
上下文向量dt可以看作是当前的query“查询”,每个节点的特征向量h(N)代表节点的query“键”,因此,在所有keyi,i=1,···,N中,可以选择与query最匹配的一个作为下一个访问的任务节点,该匹配值通过注意力机制计算得到.首先对query和key进行计算,即
则选择各个节点的概率计算为
其中:v,W1,W2是可训练的神经网络参数,softmax函数用于归一化ui以获得最终概率.
同时,概率生成过程中增加基于无人机荷电状态的屏蔽(mask)机制,如果某节点无法被选中则将其概率置零,包括以下几种情况: 1)如果节点i>0在时间t′
即剩余电量应该足够无人机前往节点i并返回基站.
图1对该解码过程进行了可视化,在图1中,节点0和3已经被选中,任务是确定下一个节点.通过当前解码器的上下文向量和来自编码器的特征向量可以计算得到选择各个节点的概率,采取贪心策略即可选择概率最大的节点,即节点1,通过该过程不断选择节点即可构造得到一条可行的无人机路径.
4 强化学习训练方法
无人机路径的构造过程可以采用马尔科夫决策过程进行建模,在第t步决策过程,无人机当前的路径π1:t-1、无人机剩余电量、各节点坐标、重要度等信息s代表问题的当前状态,智能体根据当前状态根据自身的策略pθ进行动作的决策,即选择下一步的任务节点,动作执行后产生奖赏值是收集到的任务节点重要度ri.本文中,参数为θ的深度神经网络模型代表该智能体的策略,该策略pθ根据当前状态,通过其编码器–解码器的结构输出选择各个任务节点的条件概率分布pθ(πt|s,π1:t-1),根据链式法则,无人机路径构造为
采用强化学习方法对该深度神经网络模型的参数θ进行训练.目标是在任务时间限制T内最大化无人机访问的任务点的重要度之和R(π)=,由于本文研究的路径优化问题具有时间限制,优化目标在无人机达到任务时间限制之后才可以计算得到,因此采用基于回合奖励更新的REINFORCE强化学习算法对模型进行训练,REINFORCE是一种基于蒙特卡洛学习的策略梯度算法,即采用智能体执行一回合累计的总奖励对模型参数进行更新,适合本文所研究场景.给定策略输出的概率分布pθ(π|s),REINFORCE按照如下式对模型参数进行更新:
其中b(s)代表一个基准(baseline)值,如果当前策略的表现超越了该基准值,则对该策略进行正向激励,反之亦然.本文采用一种基于贪心回合奖励的b(s)估计方法[12]对b(s)进行估计.具体地,在训练期间,将迄今为止表现最好的模型作为基准模型θ∗,在对b(s)进行计算时,将s输入至基准模型从而得到解的概率分布pθ∗(π|s),随后采用贪心策略对该概率分布进行采样,从而得到解的无人机路径,计算该解的目标值R(π∗)作为b(s)的估计.因此,b(s)可以代表模型的基准表现,从而对新的模型参数进行评价,以指导参数优化的方向.训练算法流程如下:
步骤1随机生成一组问题实例s,即一组任务节点的位置序列;
步骤2采用模型θ求解s产生解π;
步骤3采用基准模型θ∗求解s产生解π∗,计算b(s)=R(π∗);
步骤4采用式(31)更新模型参数θ;
步骤5更新基准模型θ∗,转到步骤1.
5 实验设置
5.1 实验环境参数
考虑四旋翼无人机对多个任务节点进行探测、侦查、打击的任务场景,无人机与基站之间达到阈值距离即可进行无线充电,不需要进行降落、回收、再起飞的过程,以实现全流程任务执行的无人化与自动化,仿真场景中无人机数量为1,任务节点随机分布在长10 km宽10 km的矩形区域内,任务节点具有不同的重要度,训练阶段基站固定在区域中心.仿真实验分别对50,100,150,200个任务节点的场景进行研究,任务时间限制分别为1.2 h,1.8 h,2.2 h,2.6 h.
采用文献[15]中四旋翼无人机的物理参数进行案例研究,详见表1.其中,无人机的速度设置为10 m/s,根据式(1),无人机飞行时的功率计算为62.49 W,悬停时的功率为82.46 W,无人机电池容量为3830 mAh,即43.8 Wh,电压为11.4 V.令Pt=58 dBW,Gt=58 dBi,f=915 MHz,η=0.6.
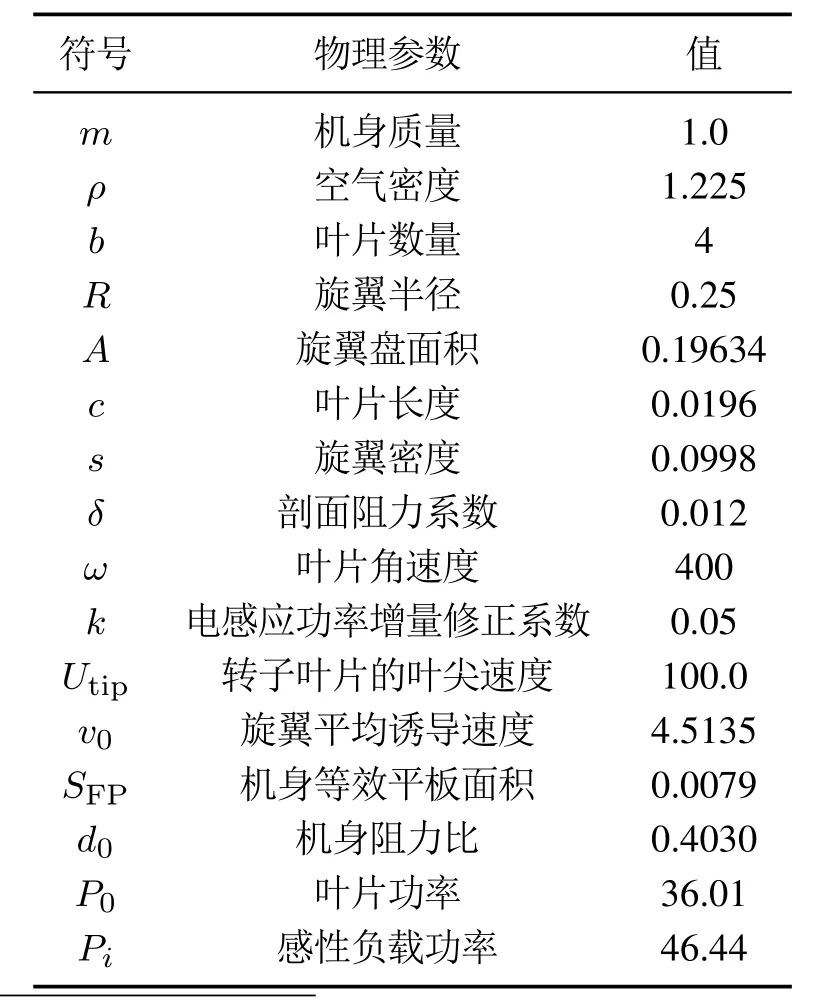
表1 无人机物理参数[15]Table 1 Physical parameters of the UAV[15]
5.2 实验算法参数
深度神经网络模型中所有的隐层维度设置为128,共训练100 代,每一代随机生成320,000 个训练实例,学习率设置为0.001,根据模型输出的概率分布pθ(π|s),采用如下3种策略构造解:
1)贪心策略:在每一步节点选择,根据pθ(π|s)选择概率最大的节点,最终构造得到一个解.
2)采样策略:从概率pθ(π|s)中进行随机采样,采样Nsample=1280次产生Nsample个解,并选择最好的一个作为最终解.
3)波束搜索(beam search,BS):类似于广度优先搜索,但搜索过程中,只保留前Nbeam个概率最大的局部解,在后续过程中仅对这Nbeam个解进行遍历,实验设置Nbeam=1000.
首先与经典启发式优化算法进行实验对比: 1)粒子群优化算法(particle swarm optimization,PSO)[19];2)蚁群优化算法(ant colony optimization,ACO);3)自适应大邻域搜索(adaptive large neighbourhood search,ALNS)[20].其代码和参数参考开源库1https://github.com/PariseC/Algorithmsfor_solving_VRP.其次与动态指针网络方法[10]进行对比,该方法是求解旅行商、车辆路径优化问题等问题的经典深度强化学习方法.
所有算法均基于Python 在配置为GTX 2080Ti GPU和Intel 64 GB 16-Core i7-9800X CPU 的计算平台上进行实验,实验结果取100次随机生成问题求解的平均值,总重要度和算法运行时间作为性能指标,并对GPU时间和CPU时间分别进行对比.
6 结果与讨论
6.1 模型优化能力分析
表2–5给出了本文所提出的深度强化学习(deep reinforcement learning,DRL)方法在包含50,100,150,200个任务节点的无人机路径优化问题上的数值实验结果,针对DRL方法和动态指针网络方法,表中分别给出了贪心策略、采样策略和波束搜索(beam search,BS)策略的实验结果,并列出了PSO,ALNS,ACO这3个经典启发式算法的数值实验结果,表中分别给出了算法的GPU平均运行时间、CPU平均运行时间以及平均目标值.

表2 50节点问题实验对比结果Table 2 Experimental results on 50-node instances
由表2可见,相对于传统深度学习方法以及多个传统启发式优化方法,DRL方法在50节点的优化问题上取得了最好的优化效果,并且求解速度的大规模提升,同时使用CPU运算的情况下,DRL方法相对于传统优化算法实现了4 到10 倍求解速度的提升;能够使用GPU 加速是深度学习方法固有的优势,采用GPU 运算,DRL相对于传统优化算法实现了100到300倍求解速度的提升.
由表3–5可见,随着问题规模的增大,DRL方法的优势愈发明显,传统启发式方法只能在小规模优化问题上取得可以接受的优化结果,在200节点等大规模问题上很难收敛.在100节点的优化问题上,相对于传统优化方法,使用CPU运算能实现4到10倍求解速度的提升,使用GPU运算能够实现200倍以上求解速度的提升;在150节点的优化问题上,CPU运算时间减少了4倍以上,采用GPU加速可以实现200倍以上求解速度的提升;在200节点的优化问题上,采用CPU运算可以实现4倍以上求解速度的提升,采用GPU加速可以实现100倍以上求解速度的提升.
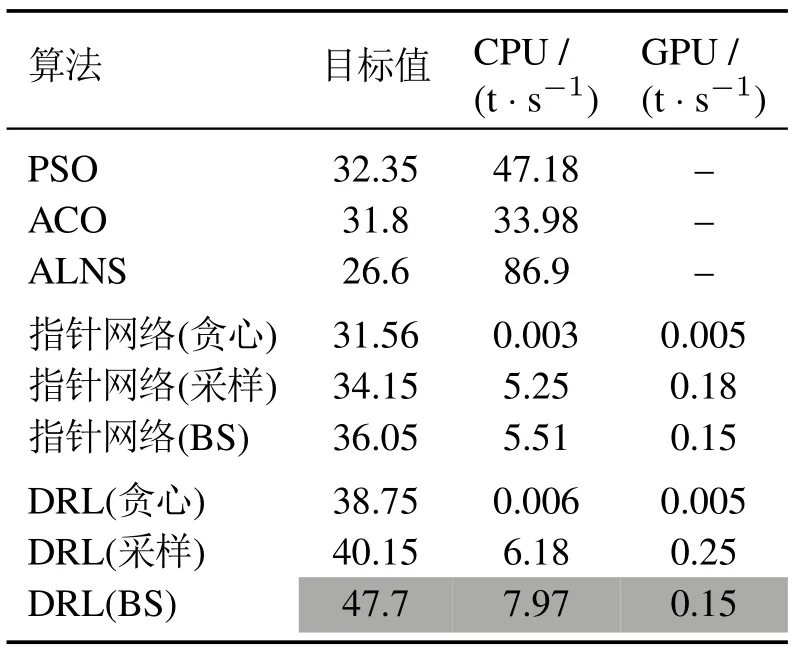
表3 100节点问题实验对比结果Table 3 Experimental results on 100-node instances
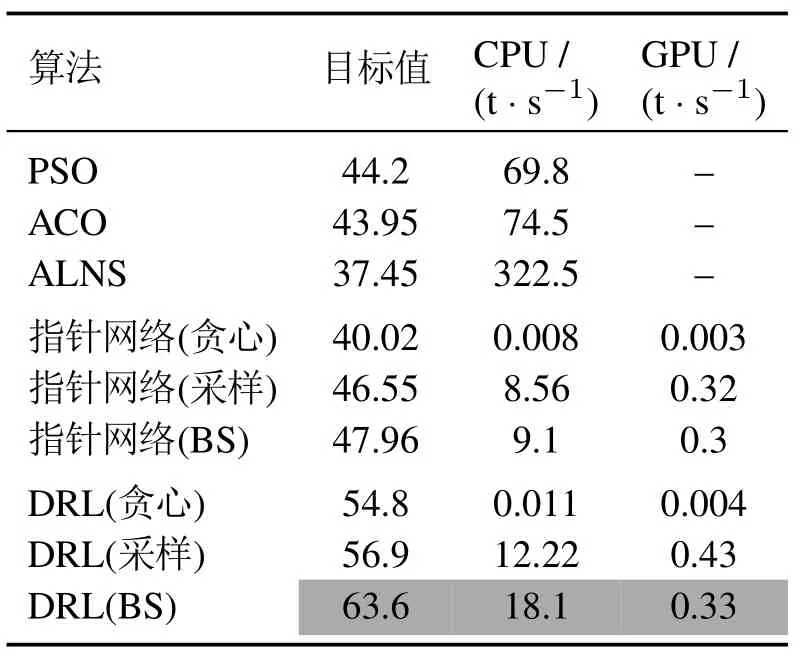
表4 150节点问题实验对比结果Table 4 Experimental results on 150-node instances
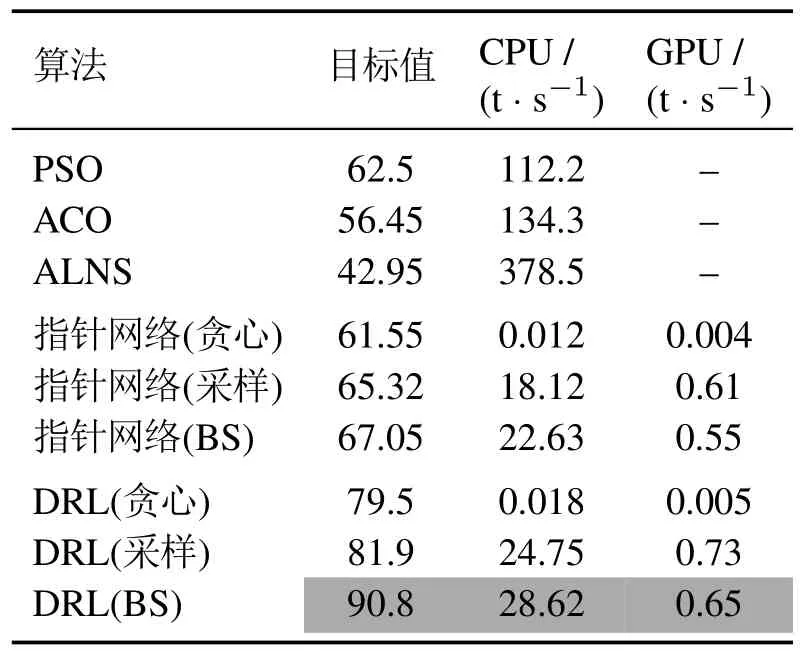
表5 200节点问题实验对比结果Table 5 Experimental results on 200-node instances
此外,从实验结果可见,经典的动态指针网络深度学习方法的求解速度略快于DRL方法,相对于指针网络模型,本文设计的编码器–解码器结构更加复杂,因此增加了运算时间,但是能够有效提高模型的优化能力,DRL方法在所有测试问题上均显著优于指针网络模型,由于求解时间的增加仅为毫秒级,因此不影响该方法求解速度快的优势.
综上可见,本文所提方法的优化能力超越了全部对比算法,同时,在相同GPU运算环境的条件下能够实现4倍以上求解速度的提升,使用GPU加速的条件下能实现100倍以上求解速度的提升.
6.2 解构造策略分析
由上述实验结果可见,不同解构造策略对于解的质量和求解时间存在较大影响.贪心策略只需要进行一次神经网络的前向计算即可构造得到问题的解,相对于传统启发式方法,无需迭代搜索,因此求解速度极快,只需毫秒级运算时间即可得到较好的无人机路径.采样策略和波束搜索需要探索多个解,能够提高解的质量,但是会耗费更长的求解时间.
图3和图4分别给出了基于贪心策略和波束搜索策略得到的无人机路径,并将归一化的任务节点重要度进行了标注.波束搜索得到的路径中,绿色路径更长,并抵达了最上方具有0.79重要度的任务节点,由于总任务时间固定,相应地缩短了蓝色路径的长度;而基于贪心策略的无人机路径未访问0.79重要度的节点,将任务时间浪费在了多个重要度较低的目标上.可见通过采用波束搜索可以有效提高无人机路径的质量.
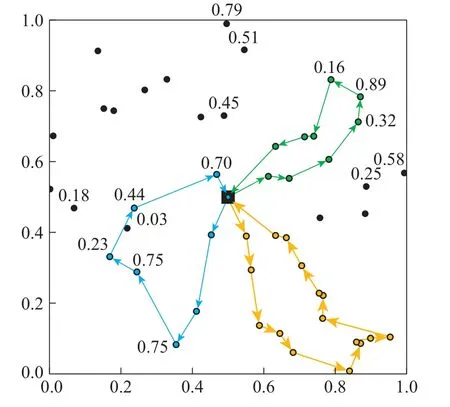
图3 基于贪心策略的无人机路径Fig.3 Solution obtained by the greedy strategy
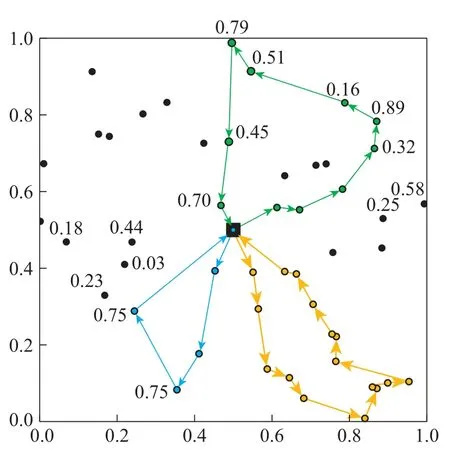
图4 基于波束搜索的无人机路径Fig.4 Solution obtained by the beam search
波束宽度是影响波束搜索性能的重要指标,当波束宽度无限大时,退化成广度优先遍历搜索方法,即通过对整个决策空间进行广度优先遍历,以得到理论最优解;当波束宽度为1时,该方法即为贪心策略,因此波束宽度对求解效果具有较大影响.
图5分析了不同波束宽度对求解时间和解质量的影响,蓝、红色线分别代表解质量和求解时间随波束宽度的变化趋势.可见随着波束宽度的增加,运算时间线性增长,但是解质量提高的幅度越来越小,因此可以通过鞍点选择合适的波束宽度.
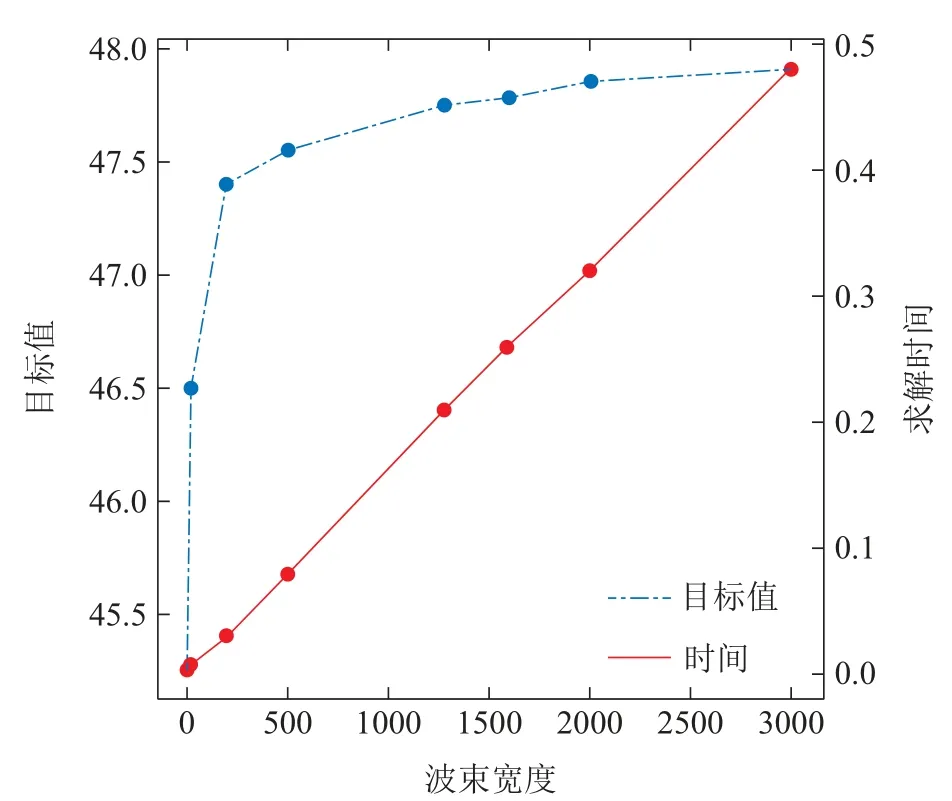
图5 不同波束宽度对求解时间和解质量的影响Fig.5 Performance analysis of optimality and solving time with different beam width.
综上,采用GPU加速的情况下,本文所提方法能够在1 s以内进行无人机路径的快速构造,从而实现考虑无线充电的无人机路径的在线实时优化,并且所得到解的质量明显超越传统的深度学习方法、粒子群、变邻域搜索等传统优化算法,在求解速度和求解精度方面得到了明显提升.
7 结论
本文基于深度强化学习方法,提出了一种考虑无线充电的无人机路径在线优化方法,可用于无人机路径的实时在线优化,克服了传统优化算法求解耗时长的局限性,在求解速度和解质量上均超越了多种传统算法.该领域的研究仍处于起步阶段,在未来的研究中,可以进一步考虑无人机的加速、减速过程以及时间窗约束,从而使得模型更加准确实际,同时,随着无线充电技术的愈发成熟、设备小型化水平的提高、充电距离的增加、充电效率的提高,进行实际无人机在线充电的测试实验也是未来亟需开展的研究内容.

